G-α-preinvex functions and non-smooth vector optimization problems

Chen Yu,Yan Xueling,Kuang Kai

(School of Mathematics and Statistics,Guangxi Normal University,Guangxi 541004,China)

Abstract：In this paper,the non-smooth G-α-preinvex function is introduced by generalizing α-invex function and G-preinvex function,and some solution properties about non-smooth vector optimization problems and vector variational-like inequality problems are discussed under the condition of non-smooth G-α-preinvexity.Moreover,it is also proved that the vector critical points,weakly efficient points and the solutions of the nonsmooth weak vector variational-like inequality problem are equivalent under non-smooth pseudo-G-α-preinvexity assumptions.

Keywords：vector variational-like inequality problems,G-α-preinvex functions,non-smooth vector optimization,weakly efficient point

1 Introduction

In this paper,we consider the following nonsmooth vector optimization problem(NVOP for short):

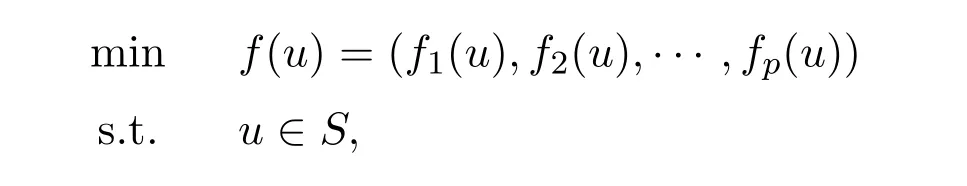
whereSis a subset of Rn,fi:S→R(i=1,2,···,p)are nondifferentiable and locally Lipschtiz functions.

A vector variational inequality was first introduced by Reference[1].Since vector variational inequality problem has widely been applied in many fields,such as vector optimization and traffic equilibrium,it has been generalized by many researchers to various directions.Among them,the vector variational-like inequality is a significant generalization about the vector variational inequality problem,which has been discussed extensively(see References[2-10]and the references therein).

The existence of the solution of variational-like inequality and the convex programming was studied in Reference[5].Reference[11]showed that the solution of variational-like inequality coincides with the solution of a certain mathematical programming problem under the conditions of the generalized invexity and monotonicity.

It is proved by Reference[2]that the above results can be generalized to the vectorial problem for Euclidean spaces.Lately,the results in Reference[2]have been extended toα-invex functions by Reference[12].Under the condition of non-smooth invexity,the relations between NVOP and vector variational-like inequality problems(VVLIP for short)are also established in Reference[13].

Reference[14]introduced a new concept ofα-pseudo-univex function,which is generalized convex function by associating the concepts ofα-invex functions and pseudounivex.Furthermore,under the assumptions ofα-pseudo-univex functions,some relationships are established between VVLIP and vector optimization problems.The results in Reference[2]are also extended to the vectorial optimization problems for Banach spaces which the domination structure is convex cones[15].

Reference[16]discussed(weak)vector optimization problems and(weak)VVLIP under the condition ofα-invexity,and established their relationships through the existence of solutions in topological vector spaces.Reference[17]discused the solution properties among vector optimization problem,Stampacchia vector variational-like inequality problem and Minty vector variational-like inequality problem under smooth(G,α)-invex functions assumption.

In this paper,we introduce the concept of non-smooth G-α-preinvex function which is a generalization ofα-invex function and G-preinvex function,and establish relationships between NVOP and VVLIP.These conditions are weaker than the earlier works existing in References[2,13-14].

2 Preliminaries

In this section,we firstly review some notations and some results about convex analysis.

For anyu=(u1,u2,···,un)T,v=(v1,v2,···,vn)T∈Rn,we define

(i)u=vif and only ifui=vi,i=1,2,···,n;

(ii)u＜vif and only ifui＜vi,i=1,2,···,n;

(iii)u≦vif and only ifui≤vi,i=1,2,···,n;

(iv)u≤vif and only ifui≤vi,i=1,2,···,n,where for at least onei,strict inequality holds.

Definition 2.1[13]A functionφ:S→R is called a Lipschitz function nearw∈Sif there exists a constantK＞0 such that

whereU(w)is a neighbourhood ofw.

φ:S→R is called a locally Lipschitz function onSif it is a Lipschitz function near any point ofS.

Definition 2.2[13]Letφ:S→R be a Lipschitz function at nearu∈S.

(i)The Clarke generalized derivative ofφatu∈Sin the directiond∈Rnis defined by

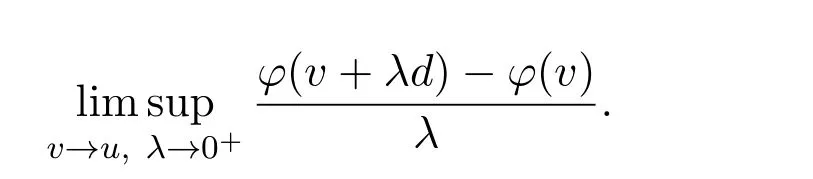
Denote the Clarke generalized derivative ofφatu∈Sin the directiond∈Rnbyφ0(u;d).

(ii)The Clarke generalized gradient ofφatu∈Sis defined by

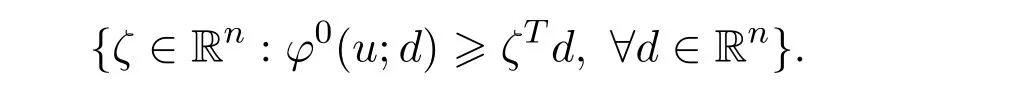
Denote the Clarke generalized gradient ofφatu∈Sby∂φ(u).

Remark 2.1Obviously,for anyd∈Rn,

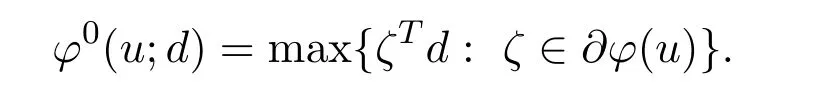
Let each functionfi:X→R be a Lipschitz function at nearu∈S,i=1,2,···,p,the Clarke generalized gradient offatu∈Sis defined by the set

Definition 2.3[13]Let the functionsη:S×S→Rnandα:S×S→R+{0},we say that the setSisα-invex set if∀u,v∈S,t∈[0,1],v+tα(u,v)η(u,v)∈S.

Before introducing the definition of G-α-preinvex,we recall the concepts of Gpreinvexity andαpreinvexity.Firstly,we give the following useful lemma,whose proofs are omitted in this paper.

Definition 2.4[18]We say that the functionG:R→R is increasing if

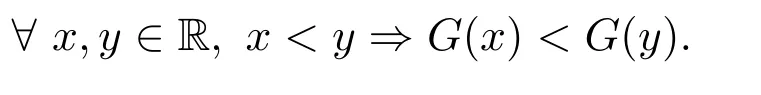
Lemma 2.1[18]G-1is an increasing function if and only ifGis an increasing function.

Definition 2.5[18-19]Let S be a non-empty invex subset of RnandG:R→R be a continuous differentiable real-valued increasing function.A functionf:S→Rpis called

(i)G-preinvex if there existsη:S×S→Rnsuch that for anyu,v∈S,

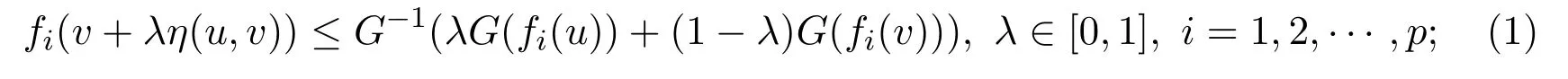
(ii)α-preinvex ifSis a closed andα-invex non-empty set and there exists the functionη:S×S→Rnsuch that for anyu,v∈S,

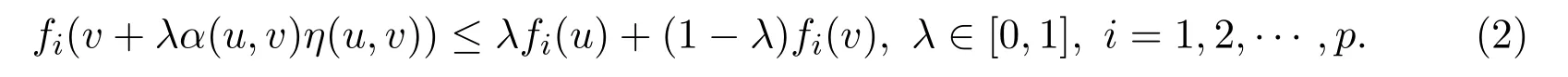
Remark 2.2It is clear that the following result can been obtained

Now,we introduce the G-α-preinvexity by combining theα-preinvexity and Gpreinvexity.

Definition 2.6LetSbe a closed and non-emptyα-invex set andG:R→R be a continuous differentiable real-valued increasing function.The non-differentiable functionf:S→Rpis called

(i)G-α-preinvex if there exist the functionsη:S×S→Rnandα:S×S→R+{0}satisfying for anyu,v∈S,

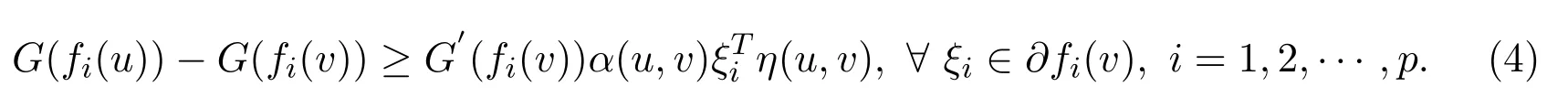
(ii)strictly G-α-preinvex if there exist the functions

satisfying for anyu,v∈S,u/=v,

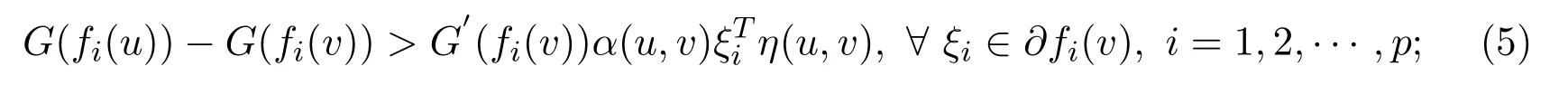
(iii)pseudo-G-α-preinvex if there exist the functions

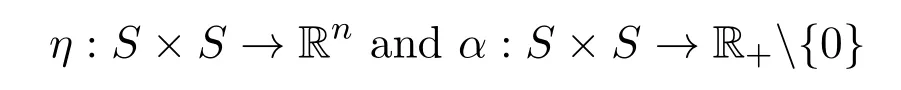
satisfying for anyu,v∈S,

Remark 2.3IfG(x)=x,then the G-α-preinvexity reduces to the nonsmooth case ofα-preinvexity[19].Ifα(u,v)=1,then the G-α-preinvexity reduces to the nonsmooth case of G-preinvexity[18].

Similar to the definitions in Reference[13],the following definitions will be utilized under the G-α-preinvexity in next analysis.

Definition 2.7For a given open subsetS⊆Rnand the G-α-preinvex functionf:S→Rp,a point∈Sis said to be

(i)an efficient(Pareto)solution to NVOP,if there does not exist av∈Ssatisfyingf(v)≤f();

(ii)a weakly efficient(Pareto)solution to NVOP,if there does not exist av∈Ssatisfyingf(v)＜f(¯u).

Definition 2.8For a given open subsetS⊆Rnand the G-α-preinvex functionf:S→Rp.

(i)For nonsmooth case,VVLIP is to find a pointv∈S,and for anyξi∈∂fi(v),there exists nou∈S,satisfying(u,v)≤0,i=1,2,···,p;

(ii)For nonsmooth case,a weak vector variational-like inequality problem(WVVLIP for short)is to find a pointv∈S,and for anyξi∈∂fi(v),there exists nou∈S,satisfying(u,v)＜0,i=1,2,···,p.

3 Main results

In the following,under the condition of G-α-preinvexity,we will establish some solution properties about VVLIP and NVOP.

Theorem 3.1LetSbe a closed and non-emptyα-invex set andf:S→Rpbe locally Lipschitz and G-α-preinvex with respect toηandα(see Definition 2.6).Supposed thatG:R→R is a continuous differentiable and increasing real-valued function.Ifv∈Sis a solution to the VVLIP with respect to the sameηand

thenvis an efficient solution to the NVOP.

ProofAssume thatvis not an efficient solution to NVOP.Then it followed from Definition 2.7 that there exists au∈Ssuch thatf(u)-f(v)≤0.In view ofG(.)be an increasing function,we know that

Sincefis G-α-preinvex,G′(fi(v))＞0(i=1,2,···,p)andα(u,v)＞0,we can conclude that there existsu∈Ssuch that this implies thatvis not a solution of the VVLIP.This is a contradiction.Sovis an efficient solution to the NVOP.

The following two theorems show that the converse theorem of the above theorem holds under some conditions.

Theorem 3.2LetSbe a closed and non-emptyα-invex set andf:S→Rpbe a locally Lipschitz function and-fbe strictly G-α-preinvex with respect toηandα.Supposed thatG:R→R is a continuous differentiable and increasing realvalued function.Ifv∈Sis a weak efficient solution to NVOP andG′(fi(v))＞0,i=1,2,···,p,thenvis a solution to VVLIP.

ProofAssume thatvis not a solution to the VVLIP.Then there existsu∈Ssuch that(u,v)≤0,∀ξi∈∂fi(v).Taking into account-fbe strictly G-α-preinvex,G′(fi(v))＞0(i=1,2,···,p)andα(u,v)＞0,we have

In view ofG-1be increasing,one getsf(u)-f(v)＜0.This contradicts with the fact thatvis a weak efficient solution of NVOP.

Based on Theorem 3.2,we can conclude that the following result holds.

Corollary 3.1LetSbe a closed and non-emptyα-invex set andf:S→Rpbe a locally Lipschitz function and-fbe strictly G-α-preinvex with respect toηandα.Supposed thatG:R→R is a continuous differentiable and increasing real-valued function.Ifv∈Sis an efficient solution to NVOP andG′(fi(v))＞0,i=1,2,···,p,thenvis a solution to the VVLIP.

Theorem 3.3LetSbe a closed and non-emptyα-invex set andf:S→Rpbe a locally Lipschitz function andfbe G-α-preinvex with respect toηandα.Supposed thatG:R→R is a continuous differentiable and increasing real-valued function.Ifv∈Sis a weak efficient solution for NVOP andG′(fi(v))＞0,i=1,2,···,p,thenvis a solution to WVVLIP.

ProofLetv∈Sbe a weak efficient solution for NVOP.Then there exists nou∈Ssuch thatf(u)＜f(v).SinceGis increasing,it follow that

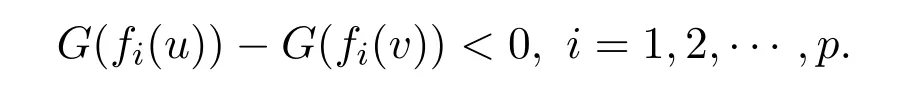
In view offbe G-α-preinvex with respect toηandα,one gets that there exists nou∈Ssuch that

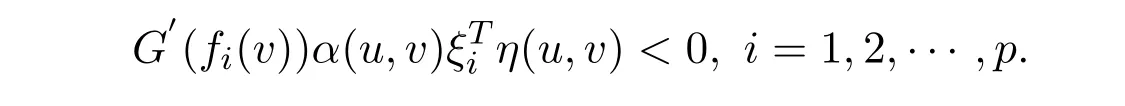
Taking into accountG′(fi(v))＞0(i=1,2,···,p)andα(u,v)＞0,we have that there exists nou∈Ssatisfying(u,v)＜0,∀ξi∈∂fi(v).Thereforevis a solution to WVVLIP.

Theorem 3.4LetSbe a closed and non-emptyα-invex set andf:S→Rpbe locally Lipschitz and pseudo-G-α-preinvex with respect toηandα.Supposed thatG:R→R is a continuous differentiable and increasing real-valued function.Ifv∈Ssolves the WVVLIP with respect toηandG′(fi(v))＞0,i=1,2,···,p,thenvis a weak efficient solution to NVOP.

ProofAssume thatvis not a weak efficient solution to NVOP.Then there exists au∈Ssuch thatf(u)＜f(v).In view ofG(.)be increasing,one gets

Sincefis pseudo-G-α-preinvex,G′(fi(v))＞0(i=1,2,···,p)andα(u,v)＞0,we can get that there existsu∈Ssuch that

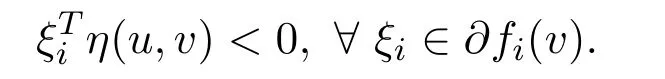
This contradicts with the fact thatvsolves WVVLIP.Thereforevis a weak efficient solution to NVOP.

Theorem 3.5LetSbe a closed and non-emptyα-invex set andf:S→Rpbe locally Lipschitz and strictly G-α-preinvex with respect toηandα.Supposed thatG:R→R is a continuous differentiable and increasing real-valued function.Ifv∈Sis a weak efficient solution to NVOP andG′(fi(v))＞0,i=1,2,···,p,thenvis an efficient solution to NVOP.

ProofSuppose thatvis not an efficient solution to NVOP.Sincevis a weak efficient solution to NVOP,then there existsu∈Ssuch thatf(u)≤f(v),In view ofG(·)be increasing,one getsG(fi(u))≤G(fi(v)),i=1,2,···,p.Sincefis strictly G-α-preinvex,G′(fi(v))＞0(i=1,2,···,p)andα(u,v)＞0,we know that there existu∈Ssuch that

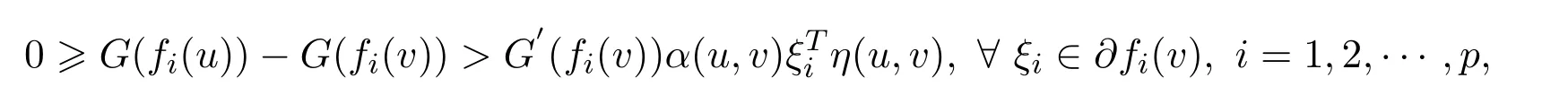
i.e.,there existsu∈Ssuch that(u,v)＜0,∀ξi∈∂fi(v).Therefore,vdoes not solve WVVLIP,which contradicts with Theorem 3.3.Hence,vis a weak efficient solution to NVOP.

Reference[20]introduced a concept of vectorial critical point for the differentiable function,and the following definition for non-differentiable function is a direct extension of the definition of their vectorial critical point.

Definition 3.1[13]We say that a feasible solutionv∈Sis a vectorial critical point for NVOP if there exists a vector∈Rnwith¯λ≥0 satisfying

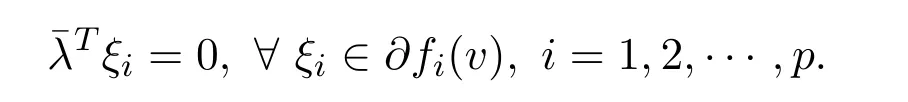
Theorem 3.6LetSbe a closed and non-emptyα-invex set andv∈Sbe vector critical point for NVOP.Supposed thatG:R→R is a continuous differentiable and increasing real-valued function.Iff:S→Rpis locally Lipschitz and pseudo-G-αpreinvex with respect toηandα,andG′(fi(v))＞0,i=1,2,···,p,thenv∈Sis a weak efficient solution to NVOP.

ProofSuppose thatv∈Sis not a weak efficient solution to NVOP.Then there exists au∈Ssuch thatf(u)＜f(v).In view ofG(.)be increasing,one getsG(fi(u))＜G(fi(v)),i=1,2,···,p.Sincefis pseudo-G-α-preinvex,we know that there exists au∈Ssuch that

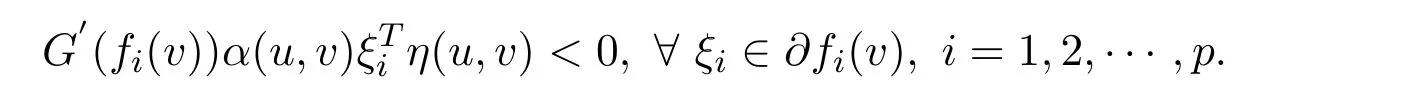
Taking account with the fact thatG′(fi(v))＞0(i=1,2,···,p)andα(u,v)＞0,one can conclude that there existsu∈Ssuch that(u,v)＜0 for anyξi∈∂fi(v).By the Gordan theorem,there exists no vector¯λwith¯λ≥0 such that=0,∀ξi∈∂fi(v),which is a contradiction with the fact thatvis a vector critical point.The proof is completed.

Furthermore,we can get the following result.

Theorem 3.7LetSbe a closed and non-emptyα-invex set.Supposed thatG:R→R is a continuous differentiable and increasing real-valued function andf:S→Rpis locally Lipschitz function and pseudo-G-α-preinvex with respect toηandαandG′(fi(w))＞0,i=1,2,···,p,w∈S.Then an weak efficient solution to NVOP is also a vector critical point for NVOP.

ProofLetv∈Sis a weak efficient solution to NVOP.Then there exists nou∈Ssuch thatf(u)＜f(v).SinceG(·)is increasing,one getsG(fi(u))-G(fi(v))＜0,i=1,2,···,p.Sincefis pseudo-G-α-preinvex with respect toηandα,then there exists no

Ifv∈Sis not a vector critical point to NVOP.Then there exists no vector¯λwith¯λ≥0 such that=0,∀ξi∈∂fi(v).From the Gordan theorem,we know that there exists ausuch that

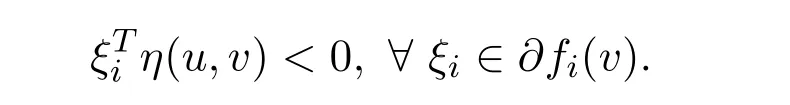
Take account intoG′(fi(w))＞0,i=1,2,···,p,w∈S,we have that

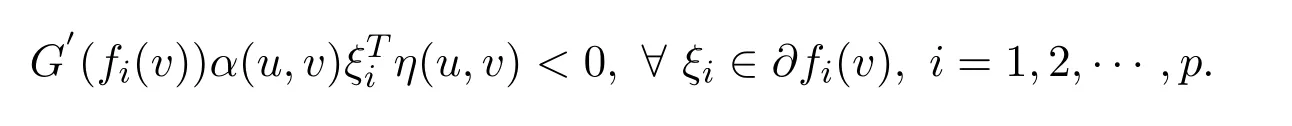
This is a contradiction.The proof is completed.

Based on the above theorems,we can establish the relationship between the vector critical points with the solutions to WVVLIP.

Corollary 3.2LetSbe a closed and non-emptyα-invex set.Supposed thatG:R→R is a continuous differentiable and increasing real-valued function,andf:S→Rpis locally Lipschitz and pseudo-G-α-preinvex with respect toηandα,andG′(fi(w))＞0,i=1,2,···,p,wherew∈S,then the weak efficient points,the vector critical points and the solutions to WVVLIP are equivalent.

4 Conclusion

In this paper,by introducing the concept of non-smooth G-α-preinvex function which is a generalization ofα-invex function and G-preinvex function,we discuss the solution properties about NVOP and VVLIP under the non-smooth G-α-preinvexity.These conditions are weaker than ones of the earlier works existing in References[2,13-14].Moreover,our results can be also extend to the vectorial optimization problems in Banach spaces.