注入式定子接地电阻分段算法应用研究

魏 扬，吴礼贵，李 琛，梁 颋，罗金嵩，陈博文

（中国长江电力股份有限公司三峡水力发电厂，湖北 宜昌 443133）

0 引言

外加20 Hz 电源定子接地保护与发电机绕组的接地位置无关，能够反映定子绕组绝缘的均匀下降，能对绝缘老化起到监督作用，在大型电站中应用较多。保护通过在发电机中性点接地变压器二次侧注入20 Hz 低频信号，采集20 Hz 电压电流信号计算接地电阻，并辅助机端零序电压判据，反映定子100%绕组一点接地故障，提高了发电机定子单相接地保护可靠性及发电机安全运行的可靠性[1-4]。

某电站发变组保护装置改造，采用了国电南自公司的DGT801U 系列装置，配置了注入式定子接地保护。保护采用导纳判据计算接地故障过渡电阻Rf，当Rf计算值低于电阻的高整定值（5.0 kΩ）时保护发信号告警，当Rf计算值小于电阻的低定值时保护动作于跳闸（0.5 kΩ）。导纳判据中接地故障过渡电阻Rf的计算值是单相接地保护的出口动作行为和监测绝缘水平的主要依据，准确地计算Rf十分必要。

1 DGT801U 注入式定子接地测量计算方法

注入式定子接地保护电气回路及等效电路图如图1 所示。图中，E20为20 Hz 注入电源，R0为注入源内阻，Rk、XK为接地变漏阻抗，Rg为接地电阻，XC为三相定子绕组对地总容抗，均折算至二次侧。U20、I20为保护装置采集的20 Hz 电压、电流，U'20为补偿掉接地变的漏阻抗后的20 Hz 电压。

图1 注入式定子接地保护

利用导纳法计算一次侧电阻、电抗，计算公式见式（1）：

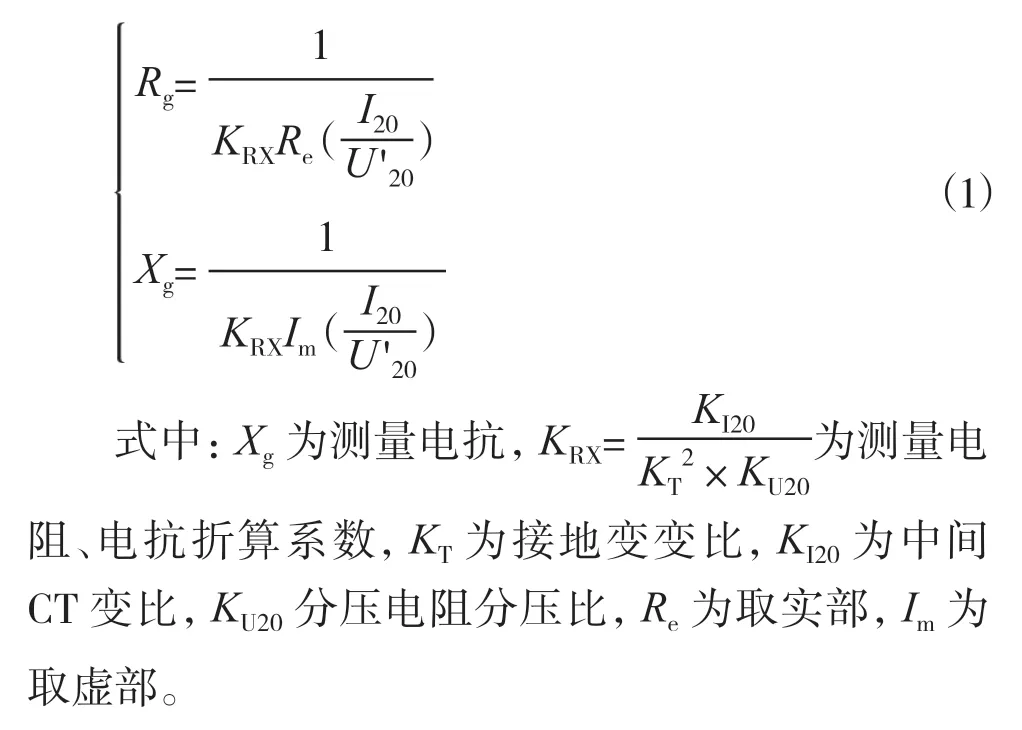
2 现场试验和数据分析

发电机主要参数为：额定电压20 kV，额定功率700 MW，发电机定子每相电容理论值3.668 μF，中性点接地变变比为20 kV/1.56 kV，副边接1.38 Ω 电阻，中间电流互感器为500/5，分压电阻为5∶1。

在完成了二次回路接线，机组一次设备恢复正常运行前的工况下，进行了模拟接地静态试验，试验数据如表1 所示。

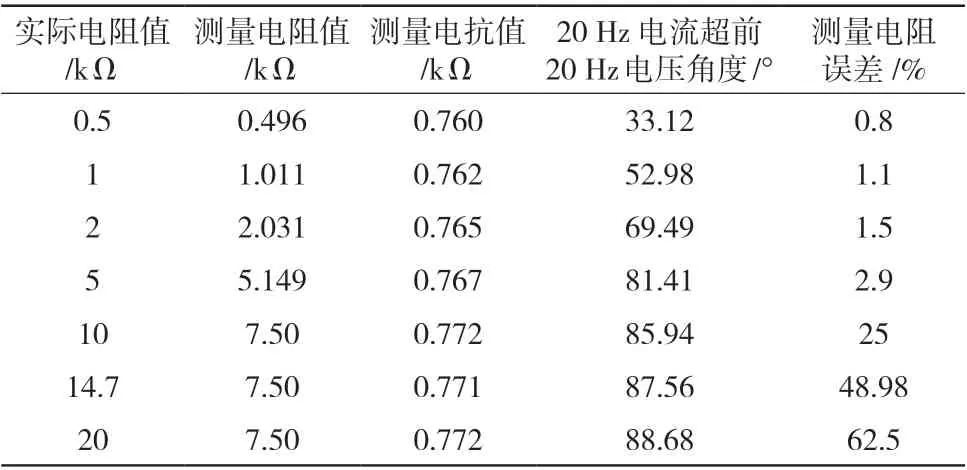
表1 第一次定子接地试验数据

通过试验发现如下规律：

（1）在小电阻接地时，测量电阻精确度较高，但在接地电阻超过7.5 kΩ 时，保护测量电阻显示值一直为7.5 kΩ，推测保护测量电阻的最大量程为7.5 kΩ。

（2）测量电抗值为0.760～0.772 kΩ，基本稳定，反映了20 Hz 频率下，定子绕组三相对地容抗的大小。

（3）随着中性点挂接电阻值的增大，20 Hz 电流超前20 Hz 电压的相位差亦随之增大，当电阻无穷大时，相位差趋近于90°。

从安全运行的角度考虑，当接地电阻大于7.5 kΩ时，保护已不能反映定子绕组绝缘水平的变化，不利于通过巡检发现定子绝缘存在的隐患。

3 原因分析及解决方案

3.1 原因分析

为保证注入式定子接地保护测量电阻稳定可靠，DGT801U 保护程序内部设定了接地电阻最大测量值，正常运行时，保护显示最大接地电阻如式（2）所示。

式中：RgMax为保护显示的最大电阻值，即接地电阻的测量量程，RInMax为内部设定值。

由式（2）可知，当RInMax越大，KRX越小时，RgMax量程越大。KRX与接地变变比KT，中间CT 变比KI20，分压电阻分压比KU20相关，其中以KT影响最大。一般情况下，接地变的选型设计参照文献[1]所述的技术条件：

（1）为有利于减小20 Hz 电源的正常负荷和提高接地保护灵敏度，接地变二次电阻RL＞1 Ω。

（2）为限制动态过电压，应满足：RL×KT2≤1/3ωCg，Cg为发电机每相对地电容。

该电站发电机中性点接地变的选型严格遵守上述条件，以某台机组为例，其接地变二次电阻为RL=1.38 Ω，每相对地电容Cg=3.68 μF，接地变变比KT=20/1.56=12.82。由于二次电阻较大，为限制系统动态过电压，故而机组接地变变比较小，使得DGT801U 注入式定子接地保护接地电阻测量量程较低，仅为7.5 kΩ。

基于以上分析，提出两种解决方案增加接地电阻测量量程：

（1）接地电阻内部设定值不变，减小电阻电抗折算系数；

（2）电阻电抗折算系数不变，增大接地电阻内部设定值RInMax。

3.2 方案1：减小电阻折算系数

DGT801U 系列保护程序实行模块化设计，为使保护程序改动最小，优先采用了这一方案。由于接地变变比KT、中间CT 变比KI20、分压电阻分压比KU20不能改变，在保护程序中再设置一个内部分压比，即电阻折算系数为：

KN为内部分压比，若分压比取3/1 或4/1 时，电阻折算系数变为原来的1/3 或1/4，内部设置值不变，接地电阻测量量程扩大为原来的3 倍或4 倍。

保护程序升级后，增加内部分压比3/1，保护接地电阻测量理论最大值为22.5 kΩ，再次模拟定子接地静态试验，试验数据如表2 所示。

表2 方案1 定子接地试验数据

由表2 可知，1 kΩ 以下电阻接地时，保护测量电阻值精度尚可；1 kΩ 以上电阻接地时，测量电阻不稳定，跃变大，且接地电阻越大，跃变范围越大。分析原因为，20 Hz 电压本身就很小，电阻折算系数中增加电压分压比3/1 后，参与接地电阻计算的20 Hz 电压值缩小为原来的1/3 倍，随着接地电阻增大，20 Hz 电流随之减小，较小的20 Hz 电压电流值参与导纳计算，微小的波动都能造成测量电阻的大幅变化，其准确度无法满足现场要求。方案1 虽然扩大了接地电阻测量量程，但其准确度不满足工程要求。

3.3 方案2：增大接地电阻内部设定值

将接地电阻内部最大设定值RInMax扩大4 倍，电阻折算系数不变，由式（2）可知，接地电阻测量量程扩大4 倍。依照此方案升级保护程序后，保护接地电阻测量值最大为30 kΩ，再次模拟定子接地静态试验，试验数据如表3 所示。

表3 方案2 定子接地试验数据

由试验数据可知：

（1）小电阻接地时，测量值稳定，但高阻接地时，测量值仍不够稳定，尤其是20 kΩ 接地时，角差接近90°，测量电阻显示值波动范围从20.1 kΩ 到最大值30 kΩ，波动较为明显。

（2）高电阻接地时，20 Hz 电流与电压的相位差有小范围波动，波动范围相较于测量电阻要小得多。

（3）测量电抗值一直较为稳定，尤其在高电阻接地时，测量电抗值稳定在0.770～0.772 kΩ。

进一步对试验结果进行分析，高阻接地时，相位差接近90°，按式（1）取倒数后的电阻测量值偏离实际电阻值较大，这是接地电阻导纳算法导致的误差。测量导纳的实部计算值较小，稍微波动后，取倒数后的测量电阻值偏差较大，甚至可能大于程序内部设定值RInMax，此时测量电阻值显示为RInMax，这就是20 kΩ 接地时测量电阻从20.134 kΩ到30.0 kΩ 跳变的原因。

4 基于20 Hz 电流电压相位差的接地电阻分段算法

4.1 算法的提出

由方案2 试验数据分析可知，测量电抗和相位差的计算值相对稳定。同时，测量电阻、测量电抗和相位差之间存在数学关系，为解决测量电阻跳变问题，本文提出了基于20 Hz 电流电压相位差的接地电阻分段算法。小电阻接地时，依然采用原算法。高电阻接地时可利用计算比较稳定的测量电抗和相位差来计算测量电阻值。

20 Hz 电流超前20 Hz 电压的相位差计算公式为式（4）：

由式（7）可知，式（1）和式（6）计算接地电阻，本质上是一样的。经试验数据验证可知，在高阻接地时，由式（1）计算接地电阻，测量电阻值波动较大，采用式（6）计算接地电阻，测量电阻值比较平稳。

综上所述，基于20 Hz 电流电压相位差的接地电阻分段算法为：

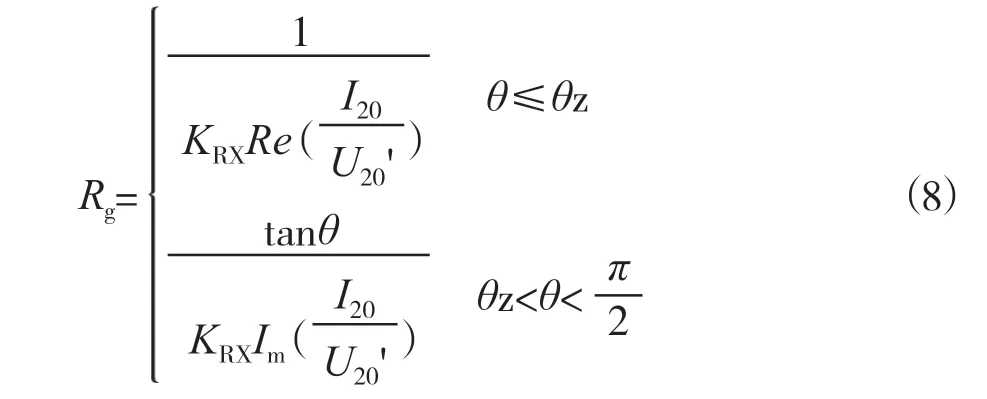
式中，θz为一设定值，一般取为85°～87°。当相位差θ小于等于θz时，采用常规接地电阻算法；当相位差θ大于θz时，利用相位差和测量电抗来计算接地电阻，受导纳实部波动影响小，能提高高阻接地时测量值的准确度。

4.2 算法的仿真及现场试验

图2 为20 kΩ 接地时测量导纳实部偏移对两种接地电阻算法的影响仿真图，测量导纳实部偏移百分比从-30%～30%。采用常规接地电阻算法，当n%从-30%变化至30%过程中，接地电阻测量值波动范围较大：从16 kΩ 变化到30 kΩ；采用改进后的接地电阻算法测量电阻值波动比较平缓，基本在误差范围内。

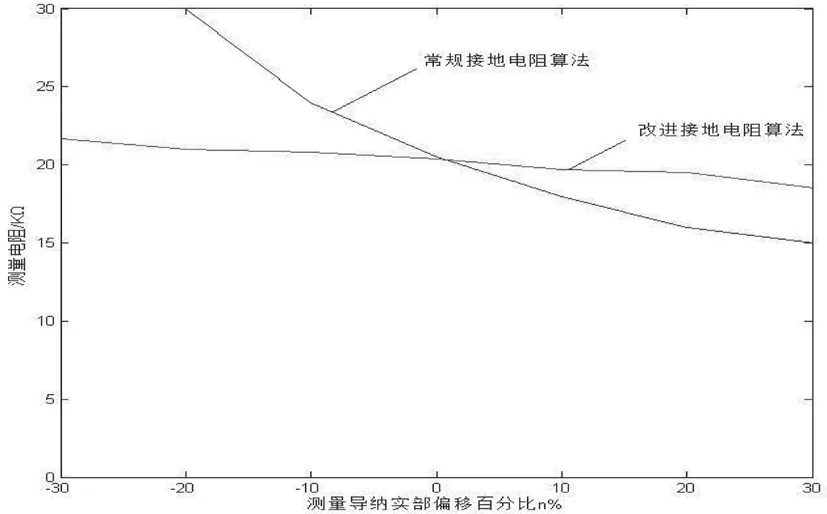
图2 20 kΩ 接地时测量导纳实部偏移对两种接地电阻算法的影响

采用上述算法进行保护程序升级后，模拟定子接地静态试验，试验数据如表4 所示。

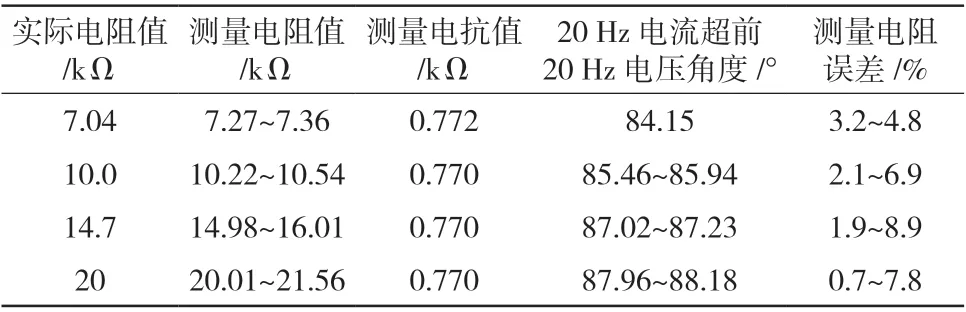
表4 改进算法后试验数据

由表4 可知，采用改进后的接地电阻算法，高阻接地时，测量电阻值比较稳定，误差基本控制在10%范围内，满足了工程实际要求。

5 结束语

本文针对注入式定子接地保护在调试过程中出现的接地电阻测量量程较小、高电阻接地时测量电阻不稳定等问题，分析了其原因，并给出了解决问题的方案，提出了基于20 Hz 电流电压相位差的接地电阻分段算法。通过对导纳算法进行补充修正，提高了故障电阻计算的准确度，提高了定子绕组绝缘检测灵敏度。