基于分子动力学的镁硅酸盐熔融特性机理研究∗

2022-08-02马芳茹陈丽娟王建江买尔哈巴阿不都热合曼

新疆大学学报(自然科学版)（中英文） 2022年4期

马芳茹，魏博†，李显,2，陈丽娟，王建江，买尔哈巴·阿不都热合曼

(1.新疆大学化学与化工学院，新疆煤炭清洁转化与化工过程重点实验室，新疆乌鲁木齐 830017；2.华中科技大学能源与动力工程学院，煤燃烧国家重点实验室，湖北武汉 430074)

0 引言

硅酸盐是地壳中含量最多的化合物，但微观结构、成分、外部环境造成硅酸盐在不同条件下表现出晶体、玻璃体及熔体等不同形态.硅酸盐在煤灰[1−2]、玻璃、水泥[3]等领域被广泛研究，其成分结构复杂、外部环境多变，使得硅酸盐宏观性质产生极大的变化.由于对产生宏观性质变化的内在机理理解不够透彻，因此，该领域引起广泛关注[4−6].熔点是硅酸盐的一个重要指标，SiO2中以[SiO4]4−为结构单元[7]，熔点为1 723 ℃.Mg是硅酸盐中重要的组成部分，与SiO2结合后可生成熔点为1 557 ℃的顽火辉石[8]（MgO·SiO2）、熔点为1 890 ℃的镁橄榄石[9]（2MgO·SiO2）等矿物质.因此，Mg的含量对硅镁酸盐的熔融特性影响显著.

很多学者通过X射线衍射[10−11]、中子衍射、拉曼[12]、红外等实验方法对Mg含量高于50 mol%的高镁组分MgO-SiO2熔体体系进行了研究.Benmore等[13]发现Mg2SiO4在熔融状态下反应压力从0.1 MPa升高至30.2 GPa时，Mg-O配位数从5.0升高到6.6.在1 600 ℃条件下，熔体中Mg-O以四面体、五面体结构为主[14]，镁离子的配位与体系组分密切相关[15].但实验分析体系微观结构往往不够具体，缺乏氧的分布、聚合度等结构信息，仅从配位数得到的信息不足以理解体系微观结构变化；同时，在现有研究中，低镁组分的结构分析领域的报道较少.

分子动力学（Molecular Dynamics,MD）研究方法是在原子、分子水平分析问题，可用于深入理解MgOSiO2熔体体系微观结构变化.在硅酸盐体系中氧的分布、聚合度等结构信息决定了硅酸盐的网络结构，进而影响到体系的熔融特性[16].其中，氧的分布可被分为三配位氧（TO）、桥氧（BO）、非桥氧（NBO）、自由氧（FO）[17].Qi代表硅酸盐体系的聚合度，i表示网络形成体所连接桥氧的个数，可分为Q0、Q1、Q2、Q3、Q4[18].

为了能够详细地分析MgO-SiO2熔体体系的微观结构，弥补目前低镁组分研究的不足，分析微观结构影响宏观性质的机理，采用分子动力学模拟的方法，在1 600 ℃条件下详细分析、总结Mg在34∼62 mol%时MgO-SiO2体系的聚合度、氧的分布、偏径向分布函数、平均键长等微观结构变化规律，为改变体系宏观性质提出理论依据，为硅酸盐宏观性质的调控提供参考.

1 计算方法

1.1 势函数的确定

势函数的选取直接影响到体系模拟结果的正确性，对于硅酸盐体系，较为常见的是Born-Mayer-Huggins（BMH）双体势函数[19]，其正确性已被广泛验证[20−22].最常使用的BMH势函数的具体形式如下：

式中：rij为粒子i和粒子j之间的距离，qi和qj分别为粒子i和粒子j的有效电荷，Aij为粒子i和粒子j之间的排斥常量，Bij为粒子i和粒子j之间的电子排斥能，Cij为粒子i和粒子j之间的范德瓦耳斯力常量.

在选择合适的势函数后，需要进一步确认势函数的势参数.在分子动力学中势参数一般分为力场参数、经验参数、非经验参数三类，其中经验参数相比力场参数而言，计算准确率较高，同时又省略了非经验参数处理库仑势的复杂步骤[23]，所以本文选取经验势参数，具体数值见表1.

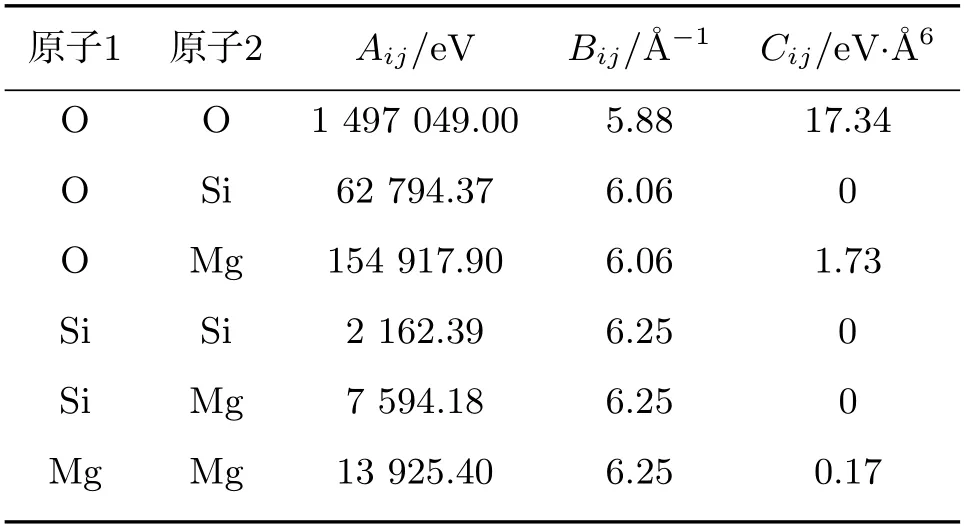
表1 熔体离子对的BMH势参数[24]

1.2 分子动力学计算

模拟体系为MgO-SiO2熔体体系，模拟软件为Materials Explorer分子动力学软件，在1 600 ℃、0.1 MPa下，根据MgO-SiO2体系FactSage二元相图选取MgO含量为34 mol%至62 mol%开展计算.初始构象为随机构象，选取2 000个粒子的正方体模型盒子，体系密度采用经验公式[25]计算，具体体系粒子数及密度见表2.

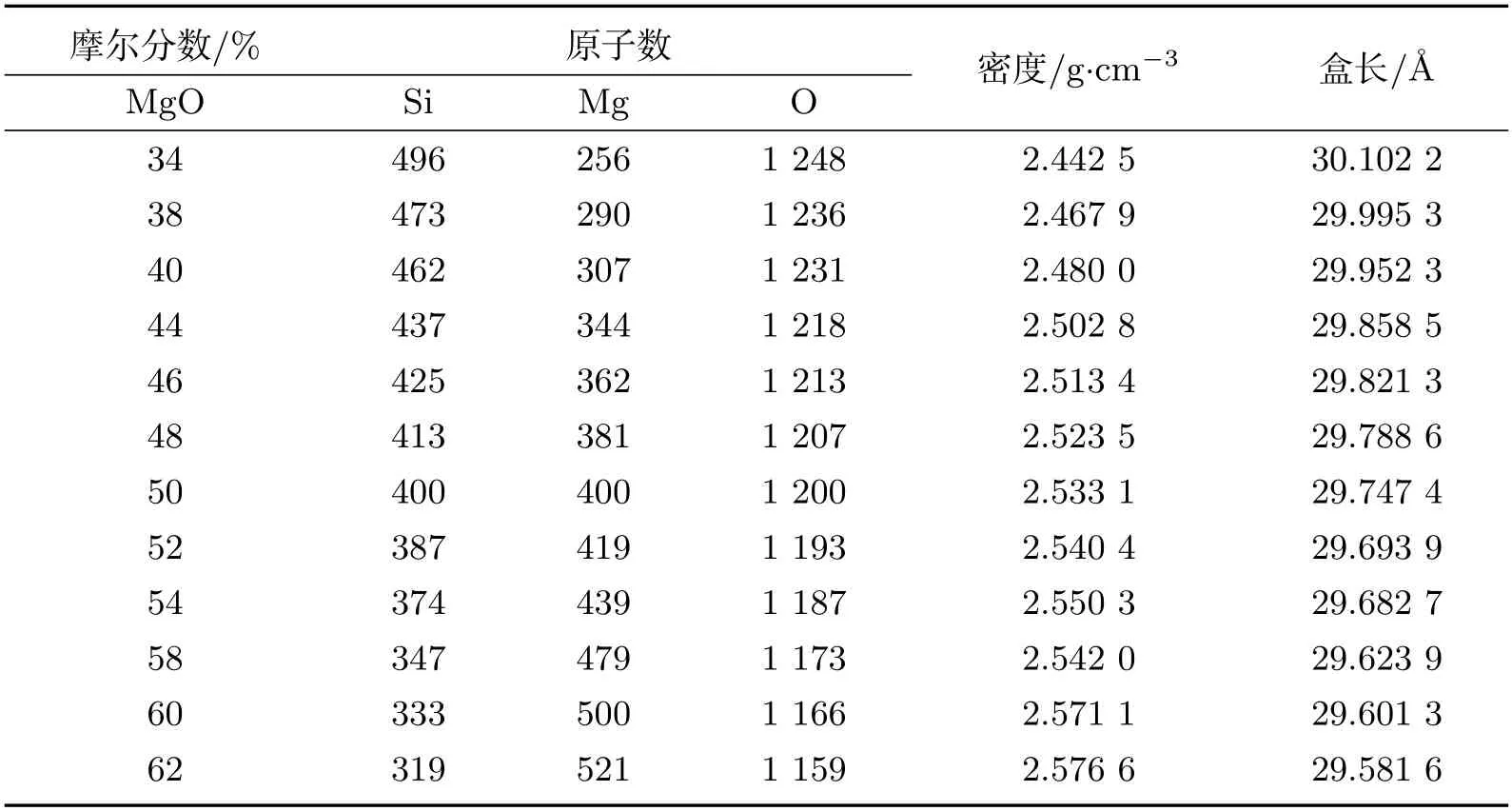
表2 体系粒子数及密度

模拟过程中采用NVT系综，使用Parrinello-Rahman[26]方法进行温度控制，Nos´e[27]方法进行压力控制，短程力的截断半径设置为10 ˚A，长程库仑力的计算采用Ewald求和方法.运行时间步长为1 fs，通过蛙跳算法每10步保存一次数据，在4 000 K的温度下运行40 000步，使体系中原子充分混合以消除初始分布状态所带来的应力，随后运行64 000步使温度降至1 873 K，最后在1 873 K下弛豫52 000步使体系达到平衡状态.在平衡状态下得到体系各粒子空间坐标，通过对坐标的分析得出体系的微观结构特征.

1.3 偏径向分布函数和平均配位数计算

在多种粒子体系中，分析非晶态固体和熔融态流体两个粒子之间的结构信息最常用的函数为偏径向分布函数（Particle Radical Distribution Function,RDF）.RDF的物理意义为在某一个粒子距离r到△r之间另一种粒子存在数量的平均数，可以反映两个粒子之间的平均键长，从而得出粒子间成键的变化趋势，计算公式如下[16]：

式中：Ni和Nj为粒子i和粒子j的个数，Nij(r)为粒子i和粒子j之间的平均配位数，V是体系总体积.平均配位数（Coordination Number Function,CN）直接反映出体系的结构变化，是衡量熔体结构的重要指标.CN通过对RDF的第一峰谷位进行积分计算得出，公式如下[28]：

1.4 离子性数量计算

对离子化合物而言，离子化合物熔融时离子键断裂，故离子化合物熔点和离子键有关.离子化合物中包含离子键、共价键等不同键的形式，各个形式所占比例不同，所成的键中离子键的比例可以通过Pauling提出的经验公式[29]计算得出，计算公式如下：

式中：Xa和Xb为a、b两原子的电负性，Iab为粒子a和粒子b所成键的离子性数量.

2 计算结果与讨论

2.1 偏径向分布函数

为了验证模拟结果的准确性，以文献中最常见Mg含量为50 mol%时的计算结果为例，在1 600 ℃下得出各粒子之间的RDF如图1所示.图1中第一峰位所对应的横坐标即表示两粒子间的平均键长，峰尖越窄表明在该处存在越集中、越具有规律性[23].由图1可得Mg-O、Si-O所对应的平均键长分别为1.97 ˚A、1.60 ˚A.本研究得到的各粒子间RDF结果和前人数据[18]对比见表3，结果与前人数据十分接近，证明了模拟的准确性.

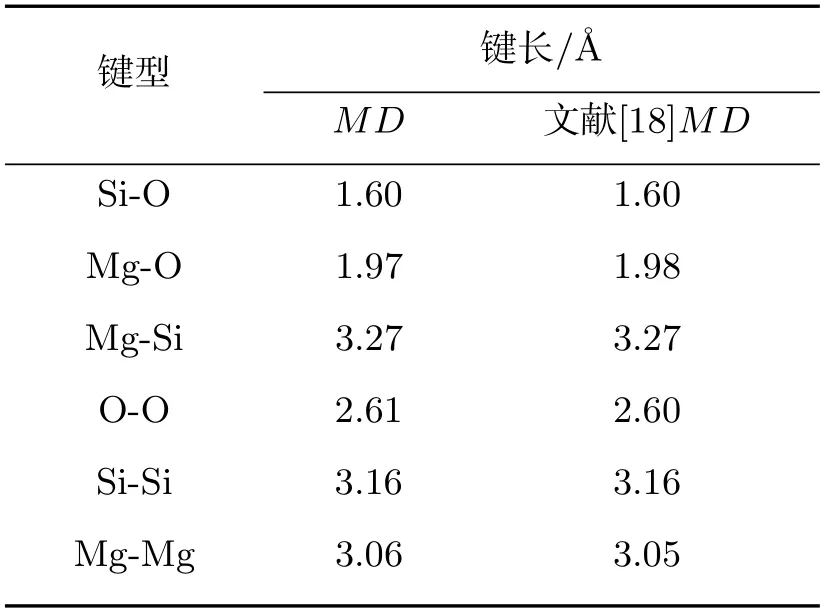
表3 平均键长与文献数据对比

由图1还可以得出，Si-O的RDF第一峰非常尖锐，说明Si-O键长分布十分集中[23]，证实了[SiO4]4−在硅酸盐中具有较高的稳定性.较为稳定的Si-O键使得SiO2熔点较高，达到了1 723 ℃.Mg-O的平均键长比Si-O长，但MgO本身熔点却超过了SiO2，达到了2 852 ℃，原因在于Mg-O、Si-O之间所成的键中离子键的比例不同，通过式（4）计算Mg-O、Si-O的离子性数量分别为0.678和0.447.离子性数量大说明成键过程中的离子键占比高[29].Mg-O比Si-O的离子性数量大，说明Mg-O离子键占比高，而Si-O处于离子键向共价键过渡状态，因此，Si-O之间所形成的离子键比Mg-O之间的离子键更易断裂.

1 600 ℃下Mg含量从34 mol%变化至62 mol%时，Mg-O和Si-O之间的RDF如图2所示.由图2（a）Mg-O之间的RDF结果可知，随着Mg含量的增加，Mg-O第一峰位从1.97 ˚A移动到2.01 ˚A，说明Mg-O之间平均键长逐渐增大.镁离子在体系中既是网络破坏体，又是电荷补偿体，分子轨道计算结果表明：形成电荷补偿体时Mg-O键长有所增加[23]，导致Mg-O键长增大.同时，第一峰的尖锐程度降低，这说明Mg-O键长的分布范围变大、分布规律性变差，体系混乱程度增加[16].由图2（b）Si-O之间的RDF结果可知，所有比例下，第一峰位均未发生变化，位于1.6 ˚A，总体变化幅度远小于Mg-O，说明Si-O键受Mg含量影响小，Si就是硅酸盐结构中的网络形成体.

2.2 平均配位数

1 600 ℃下Mg含量从34 mol%变化至62 mol%时，Si-O和Mg-O之间的平均配位数曲线如图3所示.平均配位数即为曲线两拐点中间位置所对应的纵坐标.由图3（a）可知，Si-O在4左右有稳定的配位平台，说明Si-O以四配位为主，四配位状态下的[SiO4]4−结构稳定.由图3（b）可知，Mg含量变化对Mg-O的配位数影响较为明显，配位平台不稳定，随着Mg含量的增加Mg-O的配位数从4.19逐渐增大至5.06.将本文得到的NMg−O以Mg含量为50 mol%时作为分界线，将大于50 mol%时称为高Mg区，将小于50 mol%时称为低Mg区，分析高、低Mg含量时的NMg−O，并拟合曲线与前人数据进行对比，结果如图4所示.

由图4可知，当Mg含量大于50 mol%时，获得的Mg-O配位数拟合直线的斜率为0.04左右.较陡的斜率说明Mg含量的变化对Mg-O配位数影响较大，模拟值与前人所得数据0.032 5十分接近.但低Mg区时不同比例下Mg-O配位数拟合直线的斜率为0.023 2，仅为高Mg含量时的一半左右.这种现象出现的原因可能为当Mg含量为50 mol%时正是MgO-SiO2体系的玻璃形成区[30]，在玻璃形成区内有规则排列的网络连接结构，不易析晶、稳定性强.MgO-SiO2体系中Mg-O连接比Si-O连接更稳定，当处于玻璃形成区时体系中O2−受体系稳定性的影响更倾向于向Mg2+周围移动；同时，高Mg区Mg2+含量多，对O2−的吸引力加强，使Mg-O的配位数变化更加明显，且Mg-O的配位数随着Mg含量的增加而增大.

2.3 氧的分布

MgO-SiO2熔体体系中仅有Si为网络形成体，因此MgO-SiO2熔体体系中的BO指Si-O-Si，FO指Mg-O-Mg等.1 600 ℃下Mg含量为34∼62 mol%时体系氧的分布如图5所示.由图5可知，当Mg含量从34 mol%增加至52 mol%时，NBO含量从31%左右增加至62%，BO含量从68%左右降低至32%，FO含量从1%左右增加至6%.BO主要分解为NBO，形成大量Si-O-Mg、少量Mg-O-Mg.当体系中生成大量Si-O-Mg时，Si-O-Mg不及[SiO4]4−稳定，也没有Mg-O-Mg之间的高离子性数量，导致各离子间相互吸引变弱、结构性变差，解释了为何当Mg含量为50 mol%时生成的顽火辉石熔点仅有1 557 ℃，较纯SiO2和MgO来说熔点更低.

当Mg含量在52∼62 mol%之间时，随着Mg含量升高，BO继续降低至15%左右、FO逐步增加到19%左右，NBO变化趋势不大.说明体系开始形成大量Mg-O-Mg，Mg进一步充当网络破坏体，破坏[SiO4]4−结构.当Mg-OMg含量大量增加时，Si-O-Mg的含量变化却不大，Mg-O-Mg之间离子键占比高、键的连接稳定，是高镁含量的镁橄榄石的熔点比顽火辉石熔点高的原因.

2.4 聚合度

MgO-SiO2体系中Qi指的是硅氧四面体的分布情况，Qi的变化可以表示熔体结构的解聚程度.常压下Mg含量为34∼62 mol%时，硅氧四面体的分布情况如图6所示.当Mg含量由34 mol%增加至50 mol%时，Q4从40%左右降低至14%，Q0+Q1从不足3%升高至约20%，Q2升高了9%左右，Q3含量在36%左右，变化幅度小于3%.此结果说明聚合度较高的Q4大量解体生成Q0、Q1、Q2，[SiO4]4−结构被破坏，生成Mg-O-Si、Mg-O-Mg等，体系聚合度降低.Mg含量由50 mol%增加至62 mol%时，Q2在Mg为50 mol%时占主导地位，这与前人研究结果一致[12,15].Q3分解至约15%时，Q0+Q1升高至57%左右，其中以Q0增加较为明显，Mg-O-Mg的含量随着Q0的增加而增加，变化趋势与氧的分布变化一致.