不确定微分方程中时变参数的极大似然估计∗

张贵东，盛玉红

(新疆大学 数学与系统科学学院，新疆 乌鲁木齐 830017)

0 引言

为了解决使用随机微分方程建模时会出现当时间趋于0 时其所描述对象的速度趋于无穷的问题,文献[1]在建立不确定理论的基础之上,提出了刘过程[2],由于不确定(刘)过程的提出,不确定微分方程也被定义出来,不确定微分方程是另一种对带有噪声影响的系统进行建模的数学工具,其能够有效地避免上述用随机微分方程建模所产生的问题.不确定微分方程在很多领域得到了应用,比如最优控制[3]、谣言传播[4]等.在上述一些领域的研究与应用过程中,演化出了延迟不确定微分方程[5]、带跳不确定微分方程[6],等等.对于这些不确定微分方程来说,首要的研究问题是稳定性和解的存在唯一性.在这方面文献[7]研究了多维不确定微分方程解的存在唯一性,文献[8]研究了不确定微分方程的稳定性,文献[9]研究了多因素不确定微分方程的p-阶矩稳定,等等.其次不确定微分方程中难免会出现一些未知的参数,那么作为不确定微分方程研究的另一个部分,不确定微分方程的参数估计也被提出来.文献[10]首先利用最小二乘的思想获得了不确定微分方程的参数估计,随后文献[11]利用矩的思想得到了不确定微分方程的参数估计,但是矩估计在有些时候不能得到解,于是文献[12]就提出了广义矩估计的概念来弥补这一缺陷.以及利用离散的数据通过α-轨道的方法获得估计值[13],文献[14]提出基于解的不确定微分方程的参数估计方法,文献[15]提出高阶不确定微分方程的参数估计,值得一提的是这些方法都是用来估计常数未知参数的,那么如何来估计随着时间变化的参数,文献[16]基于改写的矩估计方法得到了时变参数的估计,然而有时候矩估计方法会失效,并且此研究也未说明获得的时变参数估计是否合理这一问题.

基于上述分析，本文提出一种新的估计时变参数的方法,即改写不确定极大似然估计法,利用样本数据得到一些固定时刻的参数估计值,然后利用拟合的思想将获得的参数估计值进行线性或者非线性拟合,从而获得时变参数估计,并且给出一种时变参数拟合函数是否合理的判断方法,即要求获得的时变参数拟合函数使得所有样本数据都落在两条α-轨道之间.

1 预备知识

这个部分将介绍不确定理论中的一些基本定理,对于理解下文的推导以及证明十分有帮助.

定义1[2−3]假设L 是非空集合Γ 上的σ代数,集函数M:L →[0,1]称为不确定测度,若其满足下述公理:

公理1(正则性) 对于全集Γ,有M{Γ}=1,

公理2(对偶性) 对于任意的事件Λ,有M{Λ}+M{Λc}=1,

公理3(次可列可加性) 对于可数事件序列Λ1,Λ2,···,有

并将(Γ,L,M)称为不确定空间.

公理4(乘积公理) 假设(Γk,Lk,Mk) (k=1,2,···)为不确定空间,则有

其中:Λk为Γk中的任意事件.

定义2[2]不确定测度M 是一个单调递增集函数,那么对于任给事件Λ1,Λ2,如果有Λ1⊂Λ2,那么有

定义3[2]假设ξ为不确定变量,对于任给定的实数x,如果有

成立,那么Φ(x)称为不确定变量ξ的不确定分布函数.

定义4[2]假设ξ为具有正则不确定分布Φ(x)的不确定变量,则逆函数Φ−1(α)称为ξ的逆不确定分布.

定义5[2]假设ξ为不确定变量,若

两个积分中至少一个有限,那么E[ξ]称为不确定变量ξ的期望值.并且若ξ是具有正则不确定分布Φ(x)的不确定变量,那么期望等价于下面定义

定义6[2]假设ξ是具有有限期望值e的不确定变量,那么

称为不确定变量ξ的方差.

定义7[3]不确定过程Ct被称为刘过程,若其满足:

(1)C0=0 并且对于所有的样本轨道都是Lipschitz 连续的,

(2)Ct具有平稳独立增量,

(3)对于x∈ℜ,每个增量Cs+t−Cs都服从正态不确定分布N(0,t),其分布函数为

逆分布函数为

定义8[2]假设Ct为刘过程,f和g为可测实函数,则

称为不确定微分方程.

定义9[2]假设α是(0,1)中的数,如果不确定微分方程

可以求解相应的常微分方程

其中:Φ−1(α)为标准正态不确定逆分布函数

那么常微分方程(2)的解是不确定微分方程(1)的α-轨道.

2 未知时变参数的不确定极大似然估计

这一部分将推导利用观测数据得到不确定微分方程中未知时变参数的估计值.考虑带有未知时变参数的不确定微分方程

那么会有

将观测数据代入方程(4),则有

我们不妨将hi1(µt1,θt1)的值视为来自正态不确定分布N(e,σ)的m−1 个样本,N(e,σ)的不确定分布为

则其导数为

可以知道(x)随着|e−x|的增加而减少,根据不确定似然函数的定义

那么e和σ的不确定极大似然估计为求解下面这个最大化问题

从而

另一方面σ的不确定极大似然估计值,可以通过求解如下极大问题获得

例1考虑带有未知时变参数的不确定微分方程

假设有n个观测值,我们将利用m个数据对于前n−m+1 个时刻的未知参数µt和θt进行估计,具体步骤如下:

根据差分,我们可以获得

根据上述分析，可得

3 时变参数估计的合理性判断

这部分我们讨论什么样的时变参数估计是合理的可行的.就含常值参数的不确定微分方程而言，估计值的好坏可以通过样本轨道夹在α-轨道之间来说明,本文将此方法应用于含有未知时变参数的不确定微分方程中,来判断时变参数估计的合理性.首先定义含有时变参数的不确定微分方程的α-轨道概念.

定义10假设α是(0,1)中的数,如果含有时变参数的不确定微分方程

可以求解相应的常微分方程

其中:Φ−1(α)为标准正态不确定逆分布函数

那么常微分方程(8)的解是含时变参数不确定微分方程(7)的α-轨道.

在定义10 的基础上,有如下含时变参数不确定微分方程的性质.

定理1假设Xt和是含有时变参数不确定微分方程

的解和α-轨道,那么有

证明首先,对于每一条α-轨道,我们将时间间隔分成两个部分,

那么显然有T+∩T−=∅和T+∪T−=[0,+∞).一方面记

由于Ct是独立增量,T+和T−是不相交集合,那么

则∀λ∈Ω1∩Ω2,有

因此对于任意的t,有Xt(λ)≤,并且

另一方面记，

4 数值实例

这一部分我们将利用新冠肺炎数值实例来验证上述方法的可行性.

例2假设Xt表示t时刻中国累计感染新冠肺炎病例数,那么不确定新型冠状病毒传播模型[16]为

接下来对µt和θt进行不确定极大似然估计.从国家卫生健康委员会官网获取2020 年2 月13 日到3 月18 日的累计新冠肺炎病例数共35 个数据,并且将2020 年2 月13 日记为第1 天,以此类推3 月18 日记为第35 天.我们利用10 个数据对未知参数和进行估计,那么有

中国累计感染新冠肺炎病例数如表1 所示,数据来源于国家卫生健康委员会官网.

表1 中国累计感染新冠肺炎病例数

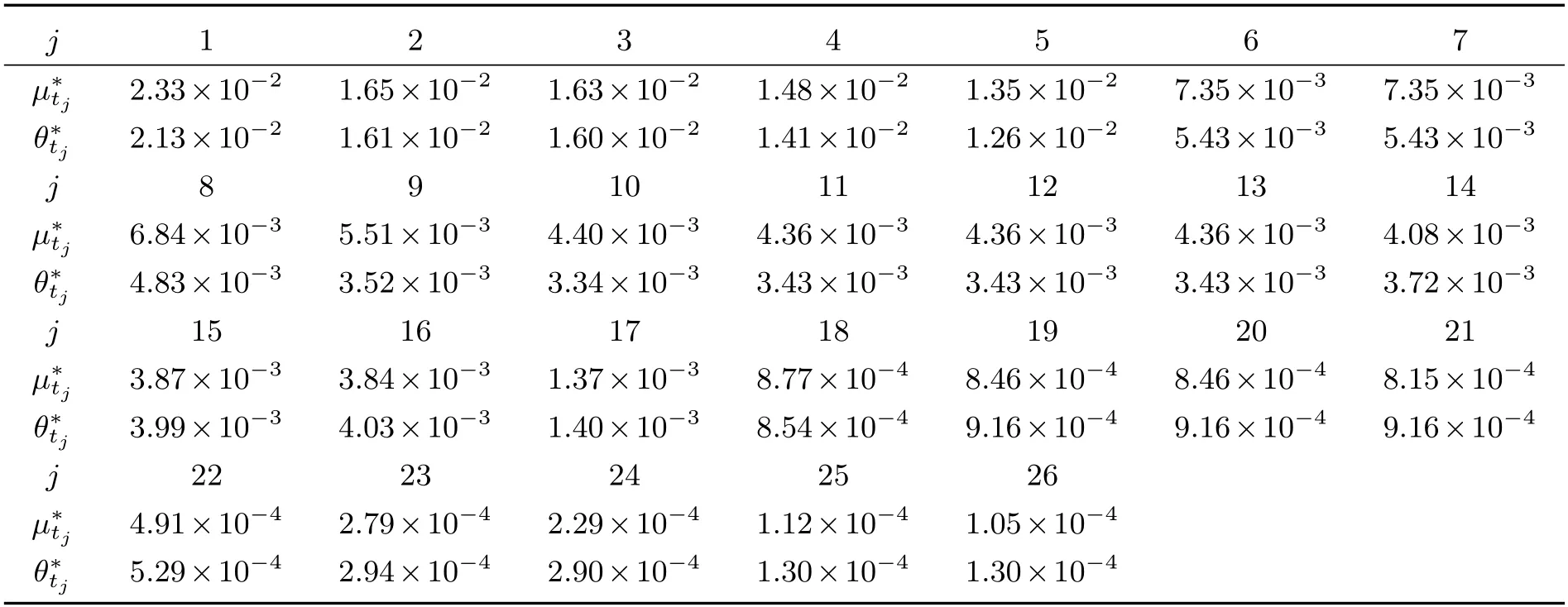
表2 µt 和θt 的不确定极大似然估计值

根据表2,利用MATLAB 做出的散点图如图1、图2 所示.

那么,根据观测估计值的散点图,我们使用逻辑递减模型

根据定义10,有

其中:Φ−1(α)为标准正态不确定变量的逆分布函数

则其α-轨道图如图3 所示.

可以看出所有的样本观测值都在0.95 轨道和0.31 轨道之间.并且其拟合图像如图4、图5 所示.

其中:R2分别为0.929 0 和0.890 8.那么知道

是合理可行的,则不确定新型冠状病毒传播模型为

同时我们利用99-方法[17]可以获得t36=36,即2020 年3 月19 日Xt的逆不确定分布,如图6 所示.

5 结论

不确定微分方程是不同于随机微分方程的另一处理动态系统问题的数学工具,在很多时候不确定微分方程的使用更加符合实际情况.本文利用不确定极大似然的思想,提出了不确定极大似然估计不确定微分方程中的未知时变参数.随后应用回归拟合的思想获得µt和θt,利用含有时变参数的不确定微分方程的α-轨道方法以及拟合优度指标R2给出了判断拟合函数是否可行的标准.最后一个数值实例,验证了方法的可行性.尽管我们利用不确定极大似然估计得到了不确定微分方程中未知时变参数的估计,但这种方法还是在估计未知常数的基础上改进的,那么未来可以尝试提出新的方法来估计未知时变参数,以及对时变参数进行不确定假设检验.