基于林地激光点云的树木胸径自动提取方法

吴杭彬，王旭飞，刘 春

（同济大学测绘与地理信息学院，上海 200092）

森林生态系统是陆地生态的一项关键组成成分，定期进行森林资源调查对其发展与保护有重要意义。林业资源调查中，胸径通常指树木距离地面1.3m 处的直径大小，它是树木的一项基础参数，不仅与树木冠幅、材积有极大的相关性，还可以用于推测树木蓄积量、生物量等其他关键林分参数［1］。传统的树木胸径参数常采取人工方式进行调查量测，借助围尺或卡尺等工具［2］，对调查森林样地中的每一棵树木依次量测与记录，但这种调查方式耗费较多的人力、物力。近些年，一些新兴的量测设备运用于胸径量测中，例如电子经纬仪［3］、全站仪［4］、CCD超站仪［5］等，但这些设备的量测方式与传统方式类似，仍需要一棵棵树木进行量测，无法实现树木批量自动化的胸径提取。

三维激光扫描技术近年来发展迅速，激光雷达设备能以非接触的方式获取林木结构参数，在林业与生态领域得到了广泛应用［6-7］。其中，机载激光雷达具备获取大范围森林资源结构的能力［8］，但更多的应用于林上结构参数反演；而地面激光扫描技术，其精准性、无损性为林下结构的测量提供了新的技术手段［9］。近年来，许多学者展开了基于TLS 数据的树木胸径参数提取研究。其中，许多研究基于Hough 变换的算法提取了树木胸径参数，其提取步骤一般是：先对林区点云进行高程归一化，再对点云进行分层并栅格化，使用Hough 变换算法对每层点云进行圆的识别，拟合二维圆形并增加判断条件检测点云中的树木位置及胸径值［10］。但是该类方法将点云数据转换为栅格数据时不可避免地会产生精度的损失，从而影响最终的提取结果。Calders 等［11］与Tansey等［12］则采用基于最小二乘圆拟合的方式对提取的单树点云树木胸径进行了计算量测。但他们的方法需要对林地数据实现单木分割的预处理步骤，这增加了额外的计算处理时间。并且，他们以单木分割结果的最低点为胸径高度的量测起点，这降低了胸径高度的计算精度。此外，Olofsson 等［13］改进了基于RANSAC模型对二维圆的拟合算法，并以此提取树木胸径值。然而当树木存在倾斜角度时，以上所述二维圆拟合的方法则会存在进行二维投影时数据冗余、模型误差增大的缺陷。

针对上述缺陷，本文提出了一种基于随机RANSAC 模型的树木胸径自动提取方法。面向大量高精度的地面激光点云数据，先通过CSF 算法提取数字地面模型，并根据该模型提取树木胸径高度的点云层，然后使用欧式距离对点云层聚类，最后对聚类后的点云簇分别采用随机RANSAC 模型进行圆柱拟合，以圆柱模型的直径作为该树木胸径。

1 树木胸径自动提取算法

1.1 树木胸径自动提取算法流程

为实现自动化的地面激光点云树木胸径参数提取，给出了如图1 的总体算法流程。该算法主要步骤为：基于CSF算法的点云滤波与林地DEM构建、基于平行DEM的树木胸径点云提取与聚类、基于随机RANSAC模型的圆柱拟合与胸径计算。

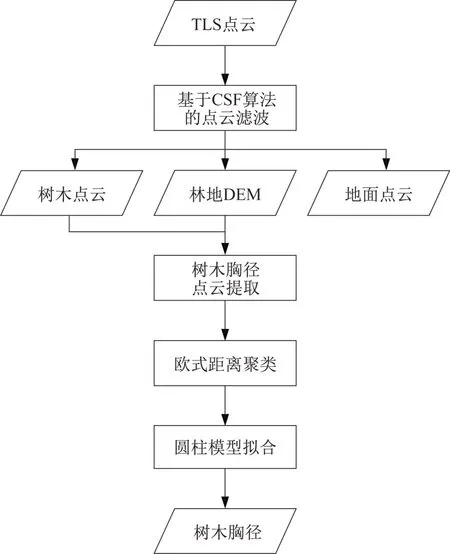
图1 树木胸径量测算法流程Fig.1 Flow chart of tree DBH measurement algorithm

1.2 基于CSF算法的点云滤波与林地DEM构建

通过地面激光扫描仪采集的激光点云数据常包含地形起伏、地表崎岖不平等情况，树木胸径的高度与地形密切相关，这为准确计算每棵树木的胸径高度带了一定困难。为获取树木胸径附近的点云即树高1.3m 处附近的点云，则需依靠准确的DEM。CSF 算法［14］是一种高效的点云地面滤波算法，它的原理是：先将处理的点云数据反转即点云中x，y坐标不变，z坐标变为相反数，所有点的坐标由（x，y，z）转变为（x，y，-z）。然后模拟出一块布料模型，根据点云场景的地形来设置布料的柔软程度，起伏越大柔软程度设置越大，反之越平坦的地形，柔软程度设置越小。此外，还需要设置栅格大小决定生成模型布料粒子的数量。最后，将布料置于反转点云上方，模拟自然下落的过程，落到点云则停止下落。再对布料粒子计算其受重力影响产生的位移和粒子间引力、排斥力产生的位移，遍历所有布料粒子，迭代终止时布料形状即为DEM。

CSF 算法参数设置简单，生成模型准确、鲁棒［15］，满足本文生成DEM 的需求。如图2 所示，林地激光扫描数据经过CSF 算法处理后，得到了树木点云、地面点云数据与该林地的DEM 结果，其中树木点云进一步用于后续的处理。

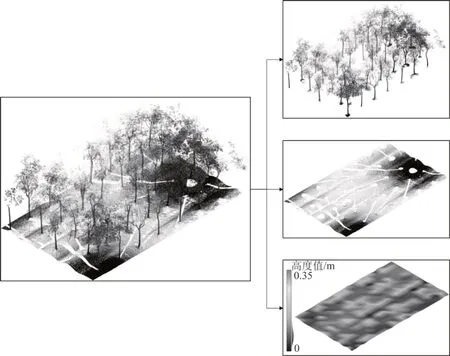
图2 基于CSF算法的点云滤波结果Fig.2 Point cloud filtering results based on CSF algorithm

1.3 基于平行DEM的树木胸径点云提取与聚类

在获取林地的DEM后，考虑到胸径计算需要在距离地面1.3m 处完成，因此本文提出了基于平行DEM 的树木胸径点云提取和聚类方法。这一方法避免了传统胸径计算过程中的单株树木提取问题，也有利于减少林地中灌木的影响。先基于原始DEM构建了平行的曲面，两者的距离为1.3m，将曲面（设曲面厚度为d）与树木点云进行叠加运算，其交集可视为树木胸径的截面。如图3 所示，左侧为单株树木点云，下方为构建的林地DEM 网格，中间为平行DEM的曲面模型，右侧为树木胸径点云的提取结果。

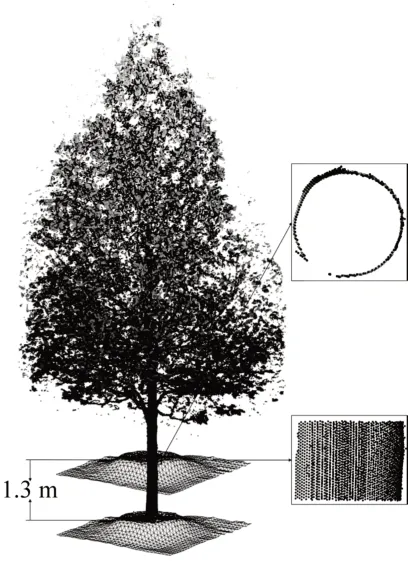
图3 单棵树木点云及胸径处点云Fig.3 One tree point cloud and point cloud at DBH

提取林地中树木胸径处的点云后，本文采用欧式聚类算法［16］对点云聚类，将林地中不同树木的树干胸径点云按单株进行区分，便于进行后续的树木胸径计算。如图4 所示，上方为林地点云的胸径处数据，下方为聚类后的各株树干胸径点云，不同灰度代表不同类别。

图4 树木胸径处点云欧式聚类Fig.4 Point cloud at DBH of trees Euclidean clustering

1.4 基于随机RANSAC圆柱拟合与胸径计算

经过1.2 和1.3 两步处理获得了每棵树木的胸径点云，考虑到树干的生态生理结构常为圆柱形且胸径处上下直径变化较小，因此本文采用圆柱模型对树干进行描述，其表达式为

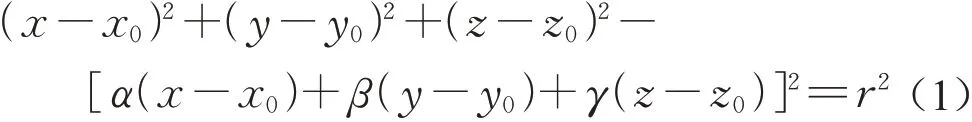
式中：圆柱模型包含7 个参数，(x0，y0，z0)为圆柱轴线上一点；(α，β，γ)为圆柱轴线的单位方向向量；r为圆柱半径。

本文对胸径点云使用随机RANSAC 模型［17］进行圆柱拟合，随机RANSAC 模型是基于RANSAC模型的一种改进模型，不同之处在于内点选取的过程中，没有像RANSAC模型用全部点计算是否为内点，而是分为两步：先随机选取部分点观察其是否为内点，再根据部分点的结果对剩余点进行计算检查。其圆柱模型拟合的计算步骤如下：

（1）假定一株树木胸径点云A（数量为n）作为圆柱模型拟合的输入点云，先计算点云A 中所有点的法线向量并随机选取A内两点，通过坐标、法线值建立初始圆柱模型［18］。

（2）对A内剩余点随机选取部分点集B（数量为m，m＜＜n-2）计算其是否符合初始圆柱模型的内点要求，如果B中所有点符合内点要求（到拟合模型的距离满足阈值要求），则对点云A中剩余的n-2-m个点检查是否符合内点要求，记录圆柱模型参数的7 个参数与内点数量，并随机取两点展开一次新的循环。如果B 中有任意一点不符合内点要求，则跳出计算并开始下一次循环。当循环结束后，内点数量最多的圆柱模型即为最佳拟合圆柱模型。

随机RANSAC模型加快了模型拟合速度，且能够保证与标准RANSAC 算法相同的拟合精度。因此，本文采用随机RANSAC模型分别对每一簇点云进行圆柱拟合，见图5，将圆柱模型的直径作为该树木的胸径值。

2 实验与分析

2.1 实验数据

实验区域位于上海市青浦区某区域，共计2 块样地，大小分别为70m×30m、60m×50m，样地中主要树种分别为鹅掌楸、无患子（图6）。

图6 实验数据采集环境Fig.6 Experiment data environment

两块样地的点云数据由Z+F 5 010C 地面激光扫描仪所获取，该扫描仪量测视野为360°×310°，量测距离为0.3～80m，量测精度在50 m 处可达±3mm。点云数据采集时先对样地中心进行了单站扫描，再对中心站周围东北、东南、西南、西北四个方向各进行一次数据扫描［19］，中心站与四周各站平均距离约15m，现场共布置12 个靶球作为配准标志物。扫描结束后，在Z+F control软件中通过标志物将四周的扫描站配准到中心站，并融合得到了完整的样地扫描数据。多站融合的点云数据有利于减少相互遮挡带来的影响，获得更为完整的树木林下结构，两块样地五站融合后的点云数量均接近两亿点。

2.2 实验方法与参数设置

基于PCL开源库［20］使用C++编程语言实现了本文算法，并基于OpenMP 第三方库［21］在CSF 算法生成DEM 的过程与多簇点云拟合模型的过程实现了并行加速运算。实验运行的硬件环境为计算机内存32GB，CPU 型号Intel（R）Core（TM）i7-9 750H CPU@2.60GHZ。

本文按图1 所示流程进行了实验，将两块样地激光点云分别作为输入，通过所提算法获得了两块样地中树木胸径的预估值。为验证和对比本文算法计算结果，采用两种对比方法。第一种方法的基本流程与本文相同，仅将圆柱拟合的步骤由随机RANSAC的拟合方法替换为最小二乘的拟合方法。第二种方法为基于Hough 变换的算法［12］，其投影的点云高度为1.28m～1.32m。

在本文算法运行过程中，CSF算法的参数为：布料柔软程度设置为2，进行陡坡处理，栅格大小设置为0.5m，算法迭代次数设置为500 次。平行DEM的厚度d设置为0.1m。欧式距离聚类的搜索距离阈值设置为0.1m，约束最小点云簇的点数设置为50。

在采集数据时，现场使用卷尺量测并记录了所有大于5cm的树木胸径数据，每棵树木量测两次，取量取胸径的平均值作为该树木的胸径值，将其视为真值，用于各算法的比较验证。

采用检测率、胸径偏差及运行时间三项指标对三种算法进行了评价。检测率为算法检测到样地树木占实际量测树木数量的比率，其计算公式为

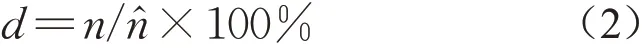
式中：n代表算法检测树木数量值，n̂代表实际量测树木数量值。检测率的大小可以反应算法的鲁棒性与有效性。

胸径偏差代表真实胸径与不同算法计算胸径之间差异的绝对值，其计算式为

式中：x表示算法提取树木胸径数值，x̂代表实际量测树木胸径数值。偏差值的大小能够反映算法量测精度的高低，与真实值的偏差越小，则精度越高，反之则越低。

2.3 DEM构建与胸径点云提取

对两样地点云数据执行基于CSF 算法的点云滤波后，生成了对应的DEM 模型，其中样地1 的林地点云与DEM 模型如图7 所示。图中还给出了样地的地面局部点云，可发现林地点云数据中地面地形并不平坦，而是存在起伏，且树与树之间存在沟壑现象，DEM的提取精度会直接影响胸径自动计算的精度。

图7 实验点云数据、DEM及局部沟壑Fig.7 Experiment point cloud data,DEM and local ravines

得到准确的DEM 模型后，构建一个平行于DEM模型的曲面模型，两者相距1.3m，通过曲面模型提取了1.25～1.35m处的胸径点云层。针对该点云层，通过欧式距离聚类得到了许多不同的点云簇，聚类结果如图8 所示，不同的灰度代表了不同的点云簇。

图8 林地胸径点云欧式聚类结果Fig8 Point cloud at DBH of trees Euclidean clustering results

2.4 树木胸径检测数量结果

将本文算法、基于Hough变换的算法以及基于最小二乘的算法提取的胸径数量按式（2）计算检测率进行评估，其结果如表1所示。结果表明，三种算法在两块实验样地中的检测率均超过了95%，达到了有效检测。本文提出的算法在两块实验样地中的检测率均为100%，即检测到了所有树木。基于Hough变换的算法与基于最小二乘的算法在样地1中的检测率相同，均漏检了2棵树木。在样地2中，其余两种方法略低于本文所提算法，基于最小二乘的算法漏检了6棵树木。在圆柱模型拟合时部分点云簇中存在小部分噪声点，基于最小二乘的算法可能无法将其忽略，拟合模型失败而导致漏检树木。

表1 不同方法的树木检测数量结果Tab.1 The detection results of trees by different methods

2.5 树木胸径量测结果

对三种不同方法在两样地中的胸径计算结果按式（3）分别计算偏差，并统计偏差的均值、最大值和最小值。

表2结果表明，三种方法的偏差最大值差异较大，其中基于最小二乘的算法在样地2 中的最大偏差为42.07cm，为三种方法在两块样地中的最大偏差，本文算法的最大偏差在两块样地中均为最小。

三种方法的偏差最小值在两块样地中的表现差异较小，均未超过0.05cm。三种方法偏差均值均小于4cm，其中基于最小二乘的算法与本文算法偏差均值均小于1cm，取得了良好的提取效果。整体来看，本文算法的量测结果优于其余两种算法。

进一步分析三种方法在两样地中所有树木胸径与实测结果的偏差值，并将其从大到小排序展示，如图9和10所示。

通过偏差结果可以发现，基于Hough 变换的算法在两块样地中的量测误差较其余两种方法更大，本文图1所示算法框架即其余两种方法所遵循框架的量测精度更高。如图9b、9c和图10b、10c所示，因为最小二乘的算法与本文方法采用了相同框架，量测偏差分布较为类似，但随机RANSAC模型拟合圆柱模型的树木胸径量测值结果与实际量测的偏差综合来看更小，因此，可以证明本文方法优于最小二乘的方法。通过比较三种方法的偏差，验证了本文所提出的基于随机RANSAC 模型树木胸径提取算法 优于其余两种算法。

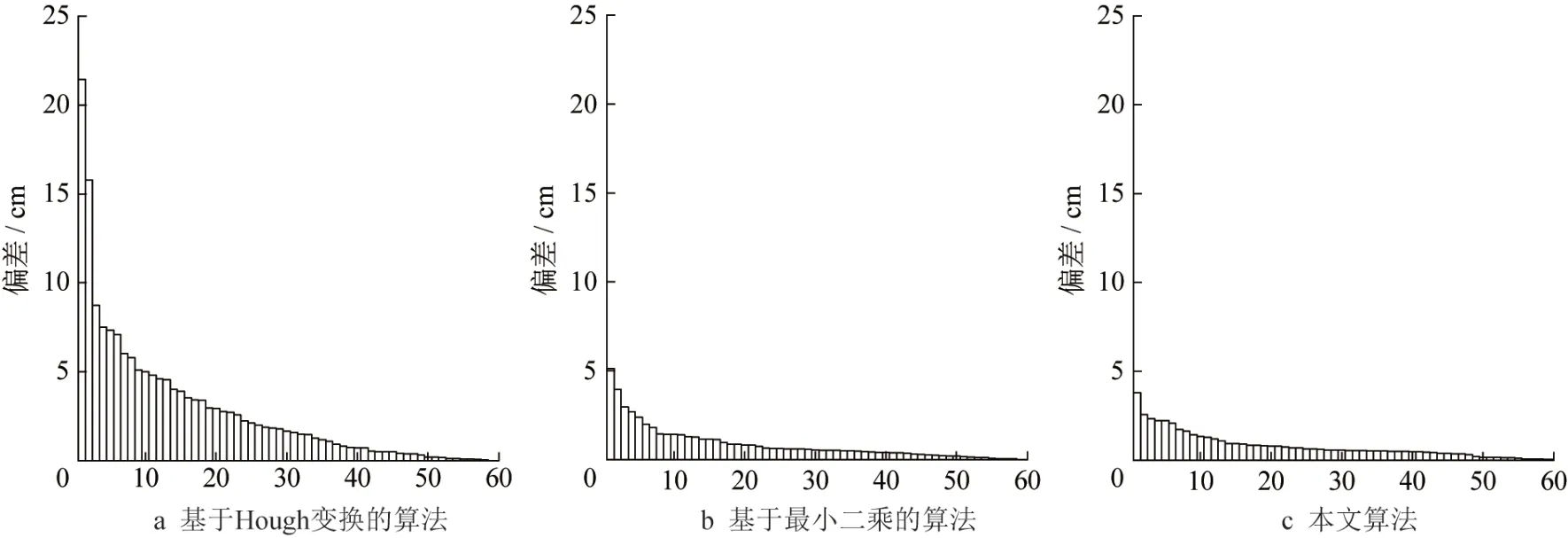
图9 样地1的胸径偏差分布Fig.9 Distribution of bias in tree DBH measurement in Plot 1

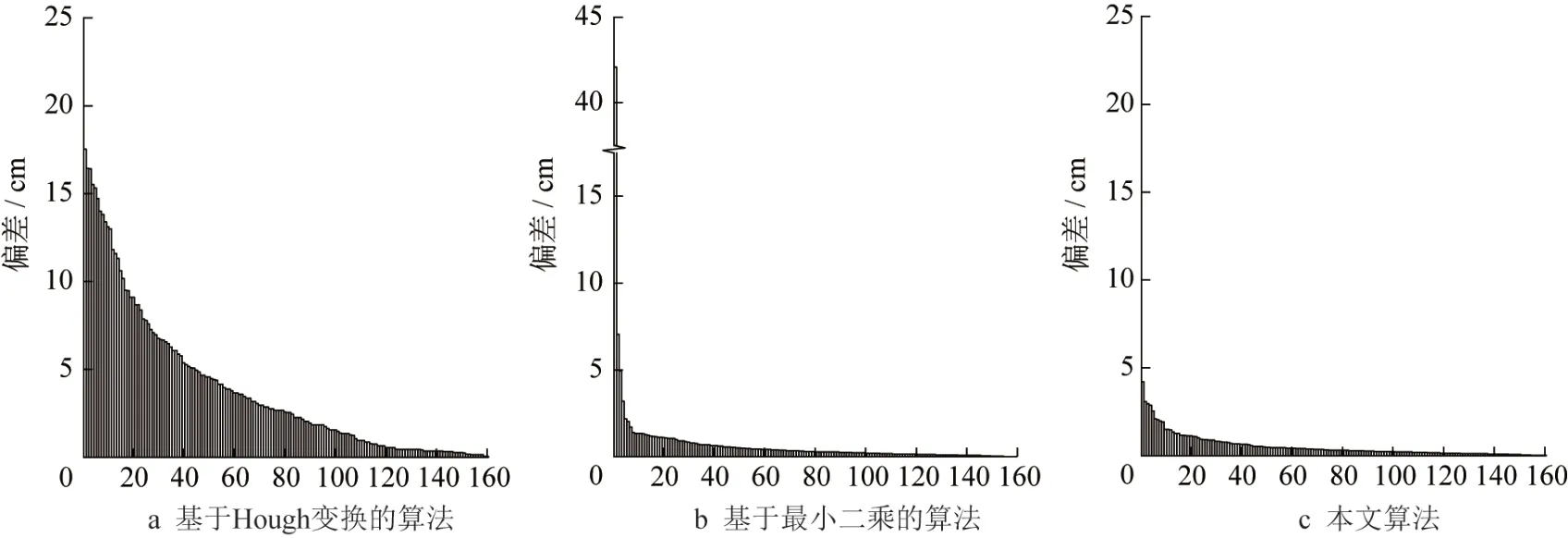
图10 样地2的胸径偏差分布Fig.10 Distribution of bias in tree DBH measurement in Plot 2

此外，考虑到本文研究结果的实际应用性，对三种算法的量测精度进行了分析比较。按照国家标准《森林资源规划设计调查技术规程》（GB/T 26424-2010）［22］中森林资源调查精度的胸径允许误差要求，本文对三种方法每棵树木胸径量测的误差进行了统计与评估，其结果如表3 所示。胸径量测误差是由上文中胸径偏差与真实胸径量测值的比值计算所得。表3 中等级A 代表了胸径量测误差小于5%的树木占总体树木数量的比例，等级B 代表了胸径量测误差为5%～10%的树木占总体树木数量的比例，等级C代表了胸径量测误差不超过10%～15%的树木占总体树木数量的比例，等级D 代表了胸径量测误差大于15%的树木占总体树木数量的比例，其中量测误差小于15%的树木符合国家标准精度等级的要求。表3 结果表明，基于Hough 变换的算法在两样地中树木量测精度明显低于其余两种方法，量测误差占比分布均匀，误差偏大的树木较多，在样地2 中超过一半的树木量测误差超过了15%，整体表现不佳。基于最小二乘的算法量测精度整体较高，在两样地中超过3/4误差均达到了5%的要求，但是仍有部分树木的量测误差超过了15%。本文算法较其余两种算法量测精度表现更加良好，在两样地中量测误差小于5%的树木数量均达到最高，并且在样地1 中所有树木的量测误差均小于15%，符合国家标准中对量测精度的要求；在样地2中，超过95%的树木量测误差符合国家标准的最低要求，整体上本文算法保证了较高的量测精度，有较高的应用可行性。

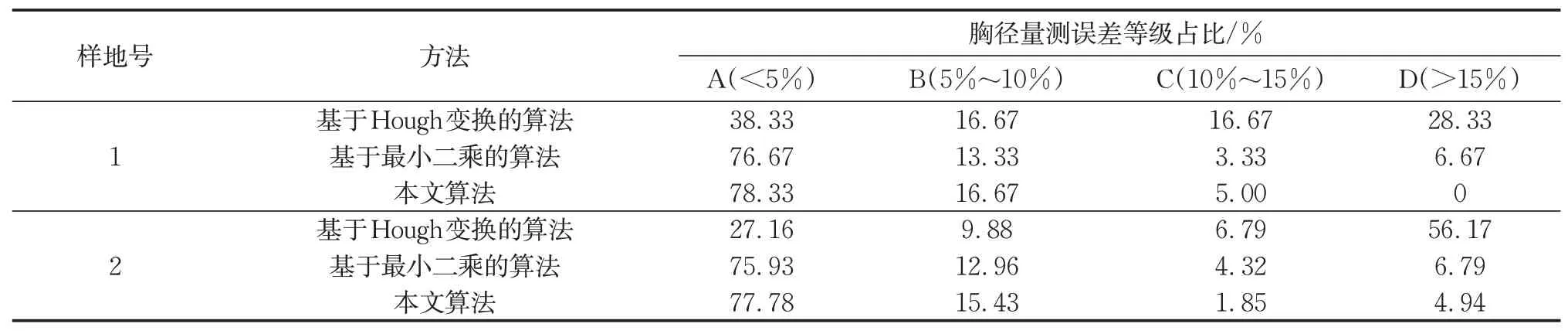
表3 不同方法的胸径量测误差等级占比Tab.3 Proportion of error grade of DBH measurement by different methods

2.6 效率比较

许多树木胸径的研究聚焦于胸径的量测精度，却很少关注方法的计算效率，而在实际应用中算法的运行效率也是一项重要的评价指标，因此表4 给出了三种方法在两样地的运行时间。时间结果表明，基于Hough 变换的算法与基于最小二乘的算法在两块样地中运行时间均超过了1 分钟，而本文所提算法均未超过30s，面对同样的数据运行时间更短，其运算效率更高。

表4 不同方法的运行时间Tab.4 The running time of different methods

3 结语

提出了一种基于随机RANSAC 模型的树木胸径提取算法，该算法包括基于CSF 算法的点云滤波与林地DEM 构建、基于平行DEM 的树木胸径点云提取与聚类、基于随机RANSAC模型的圆柱拟合与胸径计算三个步骤。使用上海市青浦区的两块林区样地点云数据对该算法进行了验证，与实际人工测量树木胸径的平均偏差分别为0.79cm 和0.52cm，95%及以上的树木量测结果符合国家标准的量测精度要求，这一结果可支持该算法的可行性。从检测率、实测数据的偏差结果与运行时间性能角度分析，本文算法均优于基于Hough变换的算法与基于最小二乘的算法。本文算法不仅精度达到了要求，且运算效率高，具有良好的应用前景。

作者贡献声明：

吴杭彬：研究方向确定、算法设计、论文修改。

王旭飞：算法设计、数据采集、数据分析、论文撰写与修改。

刘春：数据分析、论文修改。