GFRP高效铣削工艺参数的优化研究
2022-08-02袁向东伍占文林雨斌丁建文
袁向东, 伍占文, 林雨斌, 张 丰, 丁建文*
(1.乐客精密工具(太仓)有限公司,江苏 苏州 215400;2.南京林业大学材料科学与工程学院,江苏 南京 210037)
在现如今的工作与生活中,复合材料的应用越来越广泛,它是由两种或者两种以上的材料按照特定的比例混合制造而来,与传统的合金、陶瓷以及聚合物材料相比,各种各样的复合材料因其拥有的特殊性能在各行各业大放异彩[1];在家具生产行业,各种新兴的优质、经济木质复合材料就代替了传统的实木制造成为了市场主流;在工程及机床应用中,高强度比、高弹性模量、重量轻、耐腐蚀的复合材料正逐渐代替各种合金,而玻璃纤维增强复合材料就是一种应用广泛且性能十分优异的复合材料[2,3]。
玻璃纤维增强复合材料(Glass fiber-reinforced polymer,GFRP),顾名思义是以玻璃增强纤维作为增强材料,以合成树脂为基体热压成型的一种复合材料[4]。它拥有着高强度、易于制造、经济耐用、高耐腐蚀性等特点,广泛应用于航空航天、交通、娱乐、家电、电器设备、机床部件等领域[5]。
正因为GFRP有着广泛的应用领域,因此也增加了对不同加工工艺的要求。但是由于复合材料的不均匀性以及各向异性,拥有其独特的切削机理,同时会导致许多加工缺陷[6,7],如高强度的玻璃纤维会加速刀具磨损、加工表面粗糙、有裂纹以及分层,这使得研究GFRP的高效、高质量切削加工有着实际的意义[8-10]。
对于GFRP材料的切削加工性能的研究,近年来一直是国外的研究热点,Mohammad Khoirul Effendi 等[11]以切削深度、进给速度以及主轴转速作为输入参数,研究了GFRP端铣过程中的切削力并进行数学建模,切削力同切削深度进给速度成正比,与主轴转速成反比;关于切削温度,L.Sorrentino,S等[12]以切削速度和进给速度为参数,研究了GFRP钻削过程中的温度规律,最高温度随着切削速度的增加而升高,随着进给速度的增加而降低;表面粗糙度是决定加工质量和加工精度的主要关系,它主要受切削参数的影响[13],GFRP的切削破坏是塑性变形、弯曲断裂和剪切的综合作用[14],Sarma,PMMS等[15]研究了GFRP车削加工后的表面粗糙度,表面粗糙度随着切削速度的增加而降低,随着进给速度的增加而升高,与切割深度没有明显的线性联系;Khan,M Adam等[16]研究了氧化铝刀具切削加工AISI D2钢以及GFRP材料的磨损情况对比,在加工GFRP材料时,刀具的侧面磨损更大,磨损机制为强度较高的玻璃纤维的磨损和黏附。国内关于GFRP加工性能的研究目前仍然较少,郑凯等[17]研究了加工参数对GFRP铣槽加工中的切削力以及表面粗糙度的影响规律,高印寒等[18]研究了超声波精密切削GFRP的不同切削条件下加工表面粗糙度的变化规律。
为了进一步探索玻璃纤维增强复合材料铣削加工性能的研究,本文以主轴转速、进给速度以及切削深度为切削参数进行试验,以铣削过程中的切削力以及最终加工质量作为衡量指标,建立切削力以及加工表面粗糙度的数学模型,为了能获得高效率、高质量的切削加工参数,以较高的材料去除率、较小的切削力以及较优的加工质量为目标进行多因素优化,期望获得最优加工参数,为GFRP的高效切削提供一定的参考和指导。
1 材料与方法
1.1 材料
玻璃纤维增强复合材料如图1(c)(临安普力电子材料有限公司,杭州)原始尺寸为1 000 mm×1 000 mm×6 mm,后裁切成规格尺寸为140 mm×80 mm×6 mm(长×宽×厚),其主要原料为环氧树脂及电子级玻璃布。
试验用刀具为聚晶金刚石涂层(粒度10 μm)柄铣刀(乐客精密工具有限公司,太仓),刀具参数如图1(b)所示,总体长度65 mm,刀齿长度14 mm,齿数为2,直径8 mm。

图1 GFRP铣削示意图
1.2 试验设计
试验用机床为南兴装备(广东)股份有限公司生产的数控高速加工机床(MGK01),最大主轴转速为24 000 r/min,铣削方式为侧铣,试件固定在Kistler 9257b (瑞士Kistler公司)三向测力仪上,以主轴转速(9 000~15 000 r/min)、进给速度(1 500~4 500 mm/min)以及切削深度(0.1~0.5 mm)为切削参数进行试验,以铣削过程中的切削力以及最终加工质量作为衡量指标,加工后试件的表面质量由粗糙度测量仪测得。
2 结果与分析
2.1 切削力
由测力计测得的三向切削力为沿着X轴方向的Fx,沿着Y轴方向的Fy,沿着Z轴方向的Fz,由于Z轴方向上的力主要形式为系统的振动,可以由固定装置抵消,因此本文中不予讨论,切削力为Fx和Fy的合力,由公式1得出,各切削参数以及对应的切削力数值见表1。
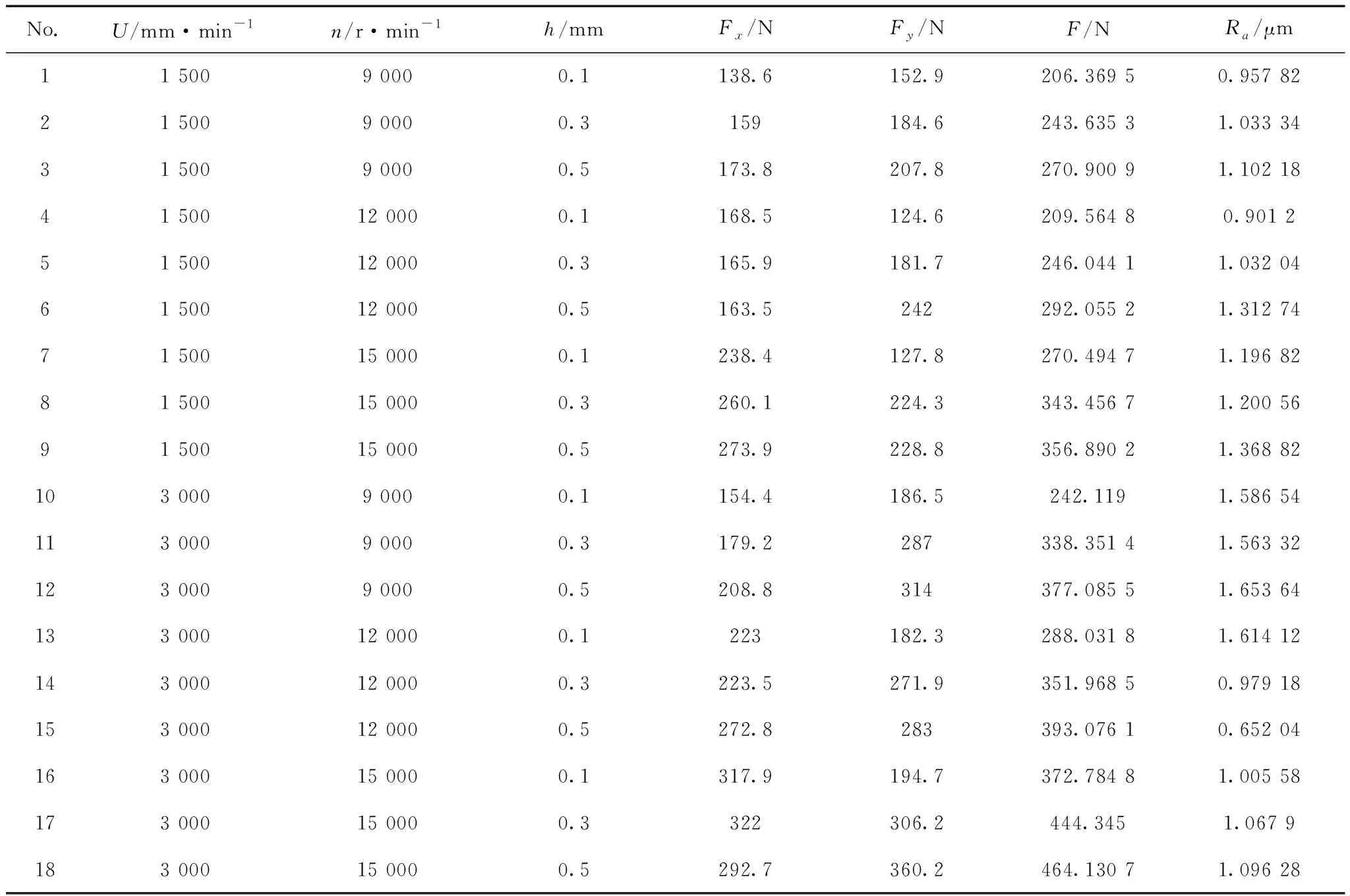
表1 切削参数及试验数据

续表1
(1)
如图2(a)所示,随着进给速度的增加,切削力呈现出明显的增加趋势,根据公式2,在相同的主轴转速下,进给速度的增加,每齿进给量Uz也会增加,单位时间内刀具的加工总量增加,因此切削力呈现出增加的趋势。
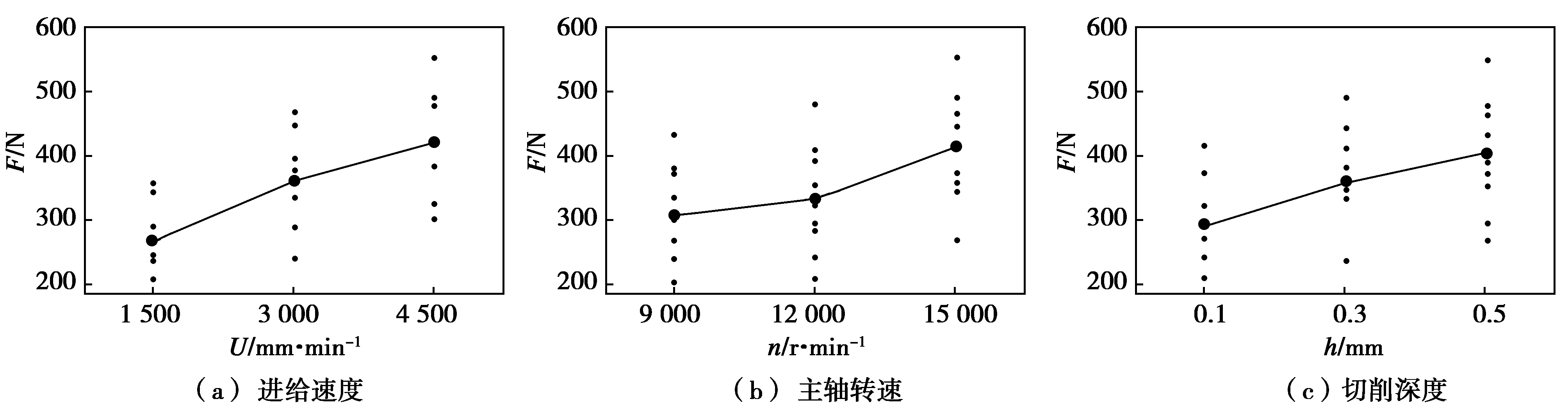
图2 切削参数对切削力的影响
(2)
式中,Uz(mm/min)为每齿进给量;U(mm/min)为进给速度;n(r/min) 为主轴转速;Z为刀具的齿数。
如图2(b)切削力随着主轴转速的增加呈现升高的趋势,这是由于玻璃纤维增强复合材料自身的性质导致的,虽然随着主轴转速的增加,由公式2得出每齿进给量增加,但是材料中的电子级玻璃布以及产生的粉末型切屑使得刀具的摩擦阻力增大,主轴转速的增加反而使得切削力增加。
如图2(c)随着切削深度的增加切削力呈现出明显的增加趋势。这是因为在进给速度和主轴转速固定的情况下,切削深度的增加,虽然刀具每次回转的每齿切削量一致,但是垂直于进给方向上的切削深度增加,导致切削量也会增加;与此同时,刀具与工件的接触弧长也会增加,导致摩擦力增大,因此切削力会随着切削深度的增加呈现出增加的趋势。
2.2 表面粗糙度
表面粗糙度是评价加工质量以及加工稳定性的一个重要因素,如图3所示得到的各切削参数对GFRP加工后表面粗糙度的影响规律图,与切削力不同,各切削参数对于表面粗糙度的影响规律并非呈现出明显的线性相关。由均值响应表2中,切削参数对于表面粗糙的影响程度的排序为切削深度>主轴转速>进给速度,其中表面粗糙度与切削深度呈现出明显的线性相关,随着切削深度的增加,表面粗糙度会随之升高,即切削质量降低。为了保证良好的加工质量,应该控制加工参数为较小的切削深度以及较高的主轴转速并同时选择合理的进给速度。
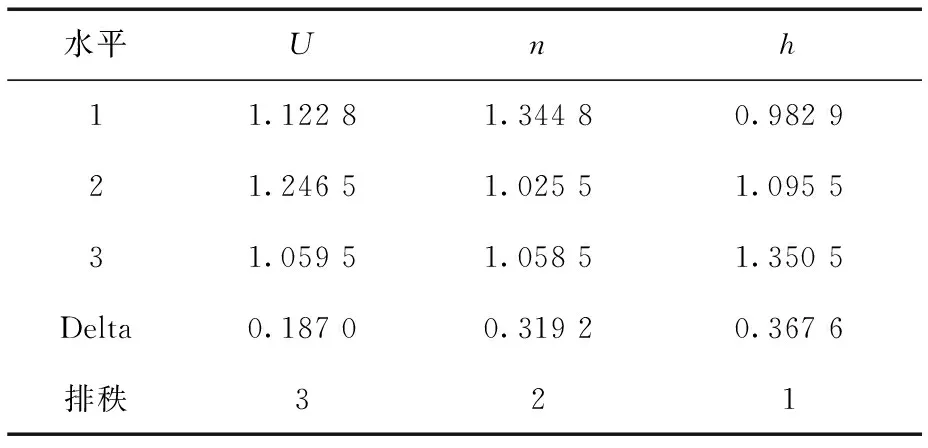
表2 均值响应表
2.3 切削模型的建立
对于同切削参数呈现出明显线性相关的切削力,以进给速度-U、主轴转速-n、切削深度-h为输入值,以切削力-F为因变量,建立线性回归方程如式3:
ln(F)=4.565 8+0.000 147U
+0.000 049n+0.800 9h
(3)
由模型的汇总数据以及方差分析(表3,4),误差项的估计标准差-S数值只有0.070 8,R2为93.70%,模型可以解释切削力数值的93.70%的变异,经过调整后的R2为92.88%,同时对于数值的预测能力达到了91.68%,切削力模型的偏差处于较低的数值,P值均小于0.05,这说明模型是显著的,各切削参数对切削力的影响顺序为进给速度>切削深度>主轴转速。

表3 切削力模型的方差分析

表4 切削力模型汇总
对于同切削参数无明显线性联系的表面粗糙度值,无法使用线性回归来进行建模,因此BP神经网络来进行模拟预测建模,实现BP神经网络预测主要从以下几个步骤出发:
①数据的预处理:包括数据的顺序调整,数据的归一化等;
②BP神经网络的构建:设置输入层数为3,输出层数为1,隐含层数为7,训练精度为1×10-5,学习速率为0.1;
③神经网络的训练以及数据预测。
如图4所示为BP神经网络的回归统计图,训练数据,验证数据以及测试数据的R值接近于1,模型拟合情况较好,但是从图5中预测数据和实际数据对比中,表5中仍然存在一定的误差,进行的三次拟合实验的平均误差分别为21.09%,14.66%,23.48%,可见普通的BP神经网络在对GFRP加工后的表面粗糙度的拟合预测上的表现较差,存在较大的误差。

表5 BP神经网络预测误差

图4 BP神经网络拟合

图5 BP神经网络预测输出与实际数值对比
为了得到更高的预测精度,使用遗传算法优化权值的方法对BP神经网络进行改进,遗传算法是一种模拟自然界“优胜劣汰,适者生存”的一种启发式算法,它的主要原理是生物进化原理引入优化参数,在所设定的编码串联群体不断地迭代,并通过遗传中的选择、交叉和变异操作对个体进行筛选,使得适应度好的个体保留,在不断的进化迭代中,新的群体继承了上一代的信息但是又优于上一代,以此规律反复循环,直至满足条件(图6),通过以下步骤实现:

图6 遗传算法优化BP神经网络流程
①种群初始化:对每个个体进行编码,每个个体成为一个实数串,由输入层同隐含层之间的连接权值、隐含层阈值、隐含层与输出层之间的权值以及输出层阈值四个部分组成的网络结构;
②适应度函数:根据每个个体得到BP神经网络的初始权值和阈值,用训练集训练BP神经网络后进行预测,将预测输出与期望输出直接绝对值误差作为个体适应度值,其计算公式为:
(4)
式中:n为网络输出节点数;yi为第i个节点的期望输出;oi为第i个节点的预测输出;k为系数。
③选择操作:使用轮盘赌法选择旧群体个体到新群体中,基于适应度比例的选择策略,每个个体i的选择概率pi为:
(5)
(6)
式中:Fi为个体i的适应度,适应度越小越好,因此在选择个体前求倒数;k为系数;N为种群个体数目。
④交叉操作:交叉操作采用实数交叉法,第m个染色体am和第n个染色体an在j位的交叉操作方法为:
amj=amj(1-b)+anjb
anj=anj(1-b)+amjb
(7)
式中:b是[0,1]之间的随机数。
⑤变异操作:选取第m个个体的第n个基因进行变异操作方法为:

(8)
式中:amax为基因amn的上限;amin为下限;f(g)是一个随机数;g为当前迭代次数;Gmax为最大迭代次数;r为[0,1]之间的随机数。
本文中种群规模设置为20,进化次数150代,交叉概率0.5,变异概率为0.02,同时BP神经网络的结构同上文一致。由图8可知,经过一床算法优化后的BP神经网络的拟合优度明显高于原始的BP神经网络,其中测试集、验证集、测试集的R值十分接近于1。在设置的150次迭代的条件下,个体的平均适应度逐渐趋近于4.5,同时最佳适应度约在0.5附近。表6中对于测试集的误差对比,可知预测的误差平均值在8.27%,远远小于原始BP神经网络平均预测误差19.74%。同时优化后的神经网络预测各组数据中的最大误差值为15.58%,远远小于原始BP神经网络中47.72%,说明遗传算法改进后的BP神经网络对于GFRP加工后表面粗糙的的预测精准度有着很大的提升,已经可以达到较为精准的预测水平。

图7 遗传算法优化的BP神经网络拟合
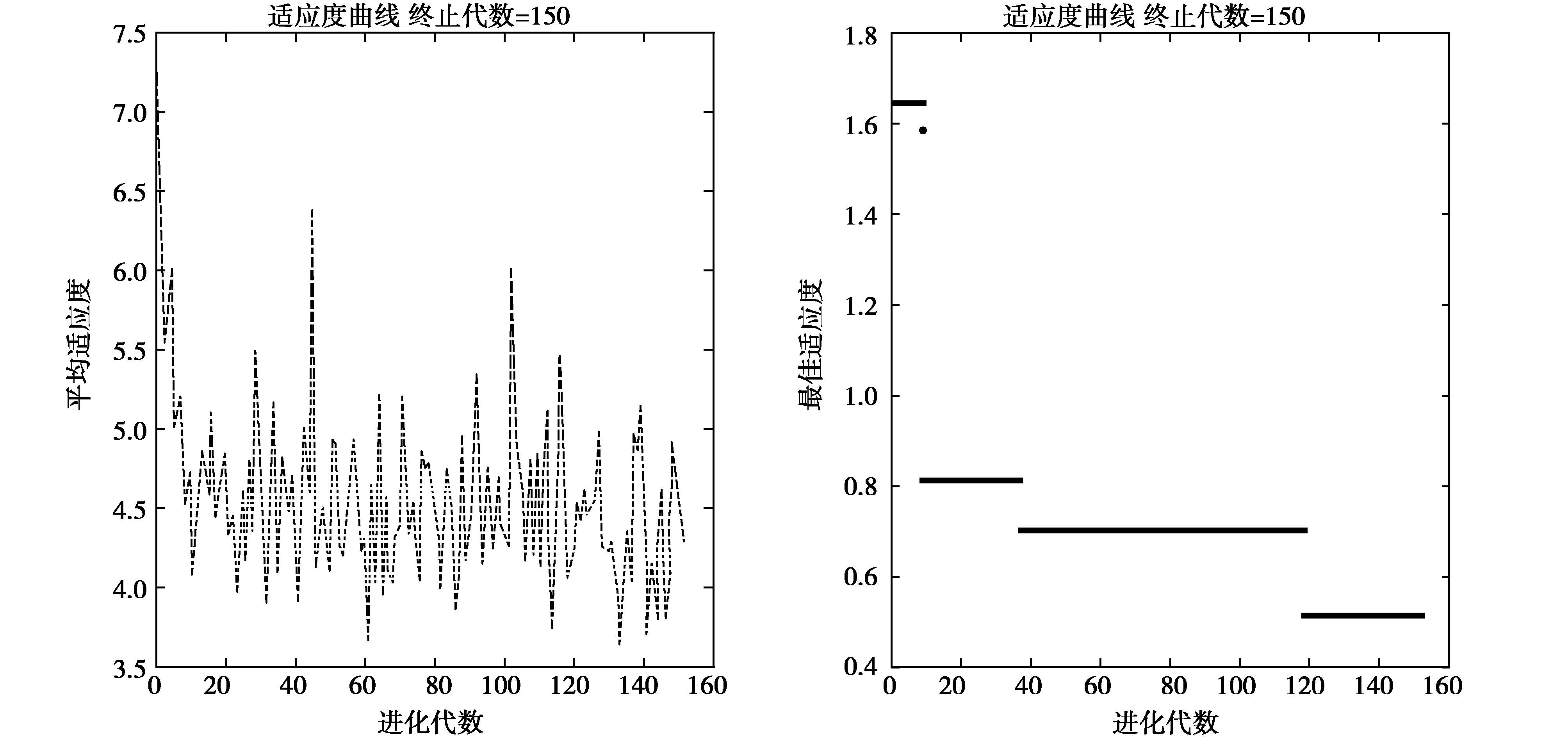
图8 遗传算法迭代

表6 遗传算法优化后预测误差
2.4 铣削参数优化
为了达到更高的切削效率,引入材料去除率(Material Removal Rate,MRR,mm3/s),来对切削效率进行定量分析,本文使用的是理想状态下的材料去除率,其计算公式为:
(9)
式中:V为去除材料的体积,mm3;t为切削时间,s;l为试件的长度,mm;δ为试件的厚度,mm。
材料去除率只和进给速度以及切削深度成正相关,所设置的切削参数的MRR如表7所示,使用遗传算法对GFRP的金刚石铣削加工进行多因素优化,目标为最小的切削力,最小的表面粗糙度以及最大的材料去除率,以期望在保证优良的加工表面质量的同时能够达到最大切削效率,预测结果以及验证结果如表8,切削力以及表面粗糙度的预测误差分别为4.62%,8.93%,误差在合理的范围内,在进给速度为4 500 mm/s,主轴转速11 181 r/min,切削深度为0.5 mm时,使用金刚石铣刀对GFRP材料的铣削加工,可以在保证较大的切削效率的同时获得良好的表面加工质量。

表7 材料去除率

表8 预测与验证对比
3 结论
本文设计了玻璃纤维增强复合材料(GFRP)的金刚石刀具铣削试验,以进给速度、主轴转速以及切削深度作为切削因素,以切削力和加工后表面粗糙度作为评价指标,运用数学建模以及神经网络的方式进行回归预测,得到以下结论:
(1)GFRP加工过程中的切削力同切削参数呈现出明显的线性相关,即切削力均随着进给速度、主轴转速以及切削深度而增加,各因素对于切削力的影响顺序为进给速度>切削深度>主轴转速;切削参数对表面粗糙度为复杂的非线性相关,表面粗糙度同切削深度呈现出明显的正相关,各切削参数对表面粗糙度的影响顺序为切削深度>主轴转速>进给速度;
(2)对切削力进行的线性回归拟合表现出较好的拟合准度以及预测精度;对于加工表面粗糙度,普通的BP神经网络预测模型拟合精度较差,平均预测误差为19.74%,使用遗传算法优化后的神经网络可以很好的提高预测精度,平均预测误差达到8.27%。
(3)以较小的切削力,较好的表面质量以及较大的材料去除率对GFRP的加工进行多目标优化,并进行试验验证,切削力以及表面粗糙度的预测误差分别为4.62%,8.93%,得到保证加工质量并获得较大切削效率的切削参数为进给速度4 500 mm/s,主轴转速11 181 r/min,切削深度为0.5 mm。
