从一道高考试题探究圆锥曲线四点共圆问题

王海燕

(甘肃省灵台县第一中学 744400)

若圆的两条弦AB，CD相交于圆内一点P,则有|PA|·|PB|=|PC|·|PD|.这就是相交弦定理.其逆定理告诉我们：若直线AB，CD相交于点P，且|PA|·|PB|=|PC|·|PD|，则四点A,B,C,D共圆.这是证明四点共圆的一个重要结论，类比于此，那么圆锥曲线上四点共圆时，应满足怎样的关系呢？

1 试题再现

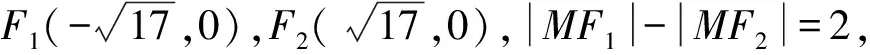
(1)求C的方程；

2 解法探析

2.1 第(1)问解析

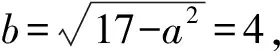
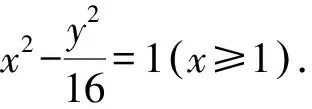
2.2 第(2)问解析

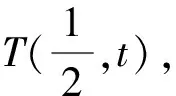
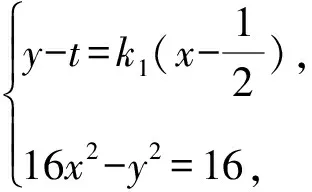
消去y并整理，得

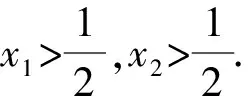
由韦达定理,得

所以|TA|·|TB|

设直线PQ的斜率为k2，同理可得

由|TA|·|TB|=|TP|·|TQ|，即有

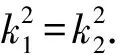
显然k1-k2≠0，故k1+k2=0.

即直线AB与直线PQ的斜率之和为0.

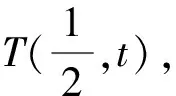
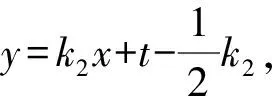
则过A,B,P,Q四点的曲线系方程为

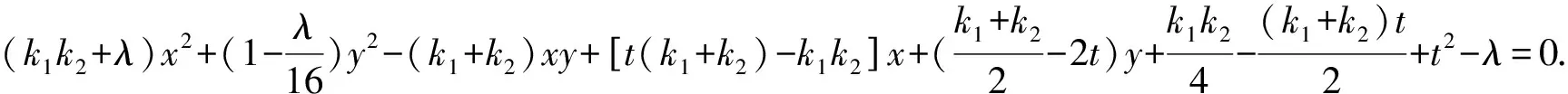
因为|TA|·|TB|=|TP|·|TQ|，

所以A,B,P,Q四点共圆.即此曲线系方程表示圆.

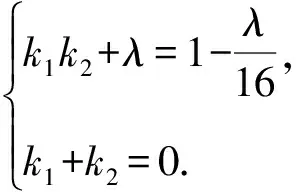
因此，直线AB与直线PQ的斜率之和为0.

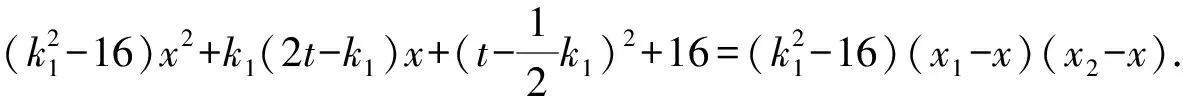
①

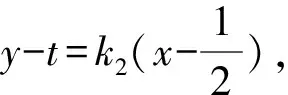
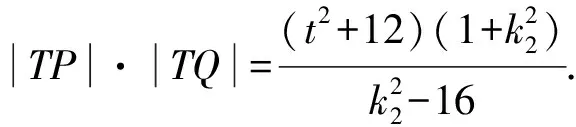
又因|TA|·|TB|=|TP|·|TQ|，

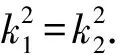
因此，直线AB与直线PQ的斜率之和为0.

(16cos2α-sin2α)t2+(16cosα-2nsinα)t-n2-12=0.

②

由于16cos2α-sin2α≠0，又直线AB与双曲线有两个交点，故方程②有两个根.

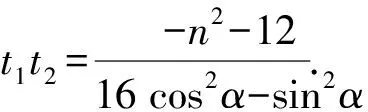
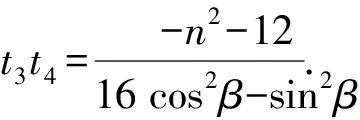
由|TA|·|TB|=|TP|·|TQ|，

可得|t1t2|=|t3t4|.

即16cos2α-sin2α=16cos2β-sin2β.

整理，得sin2α=sin2β.

又α，β∈[0，π)，所以α=π-β.

即tanα=-tanβ.所以kAB+kPQ=0.

因此直线AB与直线PQ的斜率之和为0.

3 课本溯源

这道题目可以看成是人教版课本选修4-4第38页例4的改编.

AB，CD是中心为点O的椭圆的两条相交弦，交点为P，两弦AB，CD与椭圆长轴的夹角分别为∠1，∠2，且∠1=∠2.求证：|PA|·|PB|=|PC|·|PD|.

由此推测圆锥曲线上四点A,B,C,D共圆时，直线AB与CD的倾斜角互补，即直线AB与CD斜率之和为0.

4 问题拓展

已知A,B,C,D是圆锥曲线上不同四点,若直线AB与CD有公共点,则A,B,C,D四点共圆的充要条件是直线AB与CD的斜率之和kAB+kCD=0.

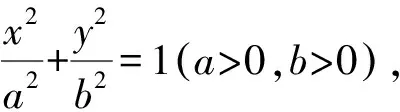
将直线AB的参数方程代入椭圆方程并整理，得到(b2cos2α+a2sin2α)t2+2(b2x0cosα+a2y0sinα)t+b2x0+a2y0-a2b2=0.

③

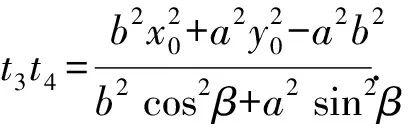
由四点A，B，C，D共圆的充要条件|PA|·|PB|=|PC|·|PD|，即得|t1t2|=|t3t4|，

整理，得(a2-b2)(sin2α-sin2β)=0.

即sin2α=sin2β.

又α，β∈[0，π)，故α=π-β.所以kAB+kCD=0.

反过来，若kAB+kCD=0，

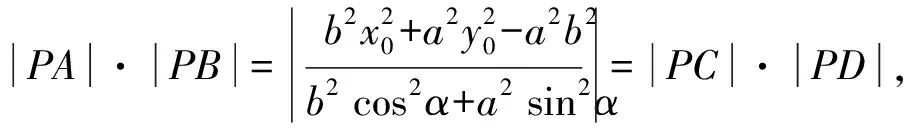
当圆锥曲线是双曲线、抛物线时，同理可证结论成立.