初中数学解题中分类讨论思想的应用

陈晔华

(江苏省无锡市塘南中学 214062)

应用分类讨论思想解答初中数学习题的难点在于如何找到分类讨论的分界点.不同的题型寻找讨论分界点的方法存在较大差别，因此教学中应做好相关习题题型的归纳以及分类讨论思想在解题中的具体应用，给学生带来良好的解题启发.

1 用于求解绝对值中的参数

例1有理数x，y满足|x|+|y|=13，|x+y|=1，求x的值.

解析∵|x|+|y|=13，|x+y|=1，|x+y|≠|x|+|y|，可知x、y必定异号.接下来需要进行分类讨论：

(1)当x>0，y<0时，则x-y=13，y=x-13，∴|2x-13|=1，则2x-13=±1，解得x=6或x=7；

(2)当x<0，y>0时，则-x+y=13，y=x+13，∴|2x+13|=1，则2x+13=±1，解得x=-6或x=-7；

反思解答绝对值问题时为更好的找到分类讨论的分界点，应认真审题，结合所学，充分挖掘隐含条件.如题目中判断出x、y异号是分类讨论的关键.

2 用于求解函数中的参数

2.1 遇有坐标轴名称不明确时需讨论

例2已知正比例函数y=k1x与一次函数y=k2x+b图象经点P(-2，1)，其中一次函数y=k2x+b图象与y轴交点坐标为A(0，3)，求直线y=k1x与直线y=k2x+b与坐标轴围成三角形的面积.

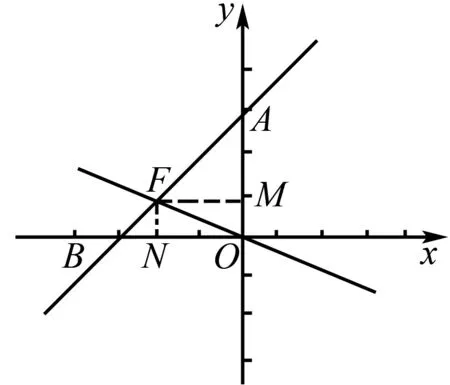
图1

∵直线y=k2x+b经点P(-2,1)与A(0,3)，∴一次函数解析式为y=x+3.

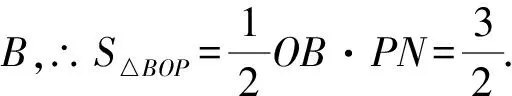
反思从已知条件可直接求出一次函数与正比例函数解析式，然而在求两条直线与坐标轴围成三角形面积时并未直接指出是x轴或y轴围成的三角形，所以可采取分类讨论思想.

2.2 遇有点位置不明确时需讨论

例3在平面直角坐标系中，已知点A(-3，0)，B(2,6)，x轴上有一点C满足S△ABC=12，求点C坐标.

解析∵S△ABC=12，∴AC=4.

(1)当点C在点A右侧，点C坐标为(1,0)；

(2)当点C在点A左侧，点C坐标为(-7,0).由此可知，点C坐标为(1,0)或(-7,0).

反思由于无法确定x轴上点C位置，故而需要采取分类讨论.

2.3 遇有k、b符号不确定时需讨论

例4一次函数y=kx+b图象与x轴、y轴分别交于A与B两点，S△AOB=4，且OA:OB=1:2，求该一次函数解析式.

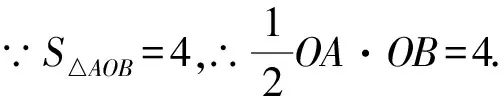
∴OA·OB=8.

∵OA∶OB=1∶2

∴设OA=x，OB=2x(x>0)，则x·2x=8，即x=2(-2舍去).

∴OA=2,OB=4.

(1)当k>0，b>0时，一次函数y=kx+b图象经第一/二/三象限，此时A(-2,0)，B(0,4)，一次函数解析式为y=2x+4.同理可得：

(2)当k>0，b<0时，一次函数解析式为y=2x-4.

(3)当k<0，b>0时，一次函数解析式为y=-2x+4

(4)当k<0，b<0，一次函数解析式为y=-2x-4.

由此可知，一次函数解析式为y=2x±4或y=-2x±4

反思因无法确定k与b符号且二者的值存在较多可能，故而需要分类讨论.

2.4 遇有增减性不明确时需讨论

例5已知一次函数y=kx+b自变量x取值范围为-2≤x≤6，对应函数值y的取值范围为-11≤y≤9，求一次函数解析式.

解析(1)若函数y=kx+b为增函数，那么一次函数y=kx+b图象两端点坐标为(-2，-11)与(6,9)，一次函数解析式为y=2.5x-6.

(2)若函数y=kx+b为减函数，函数y=kx+b图象两个端点坐标为(-2，9)与(6,-11)，一次函数解析式为y=-2.5x+4.

由此可知，一次函数解析式为y=2.5x-6或y=2.5x+4.

反思由于未明确一次函数y=kx+b中k值的符号，所以无法确定函数增减性与其对应两个端点坐标，需采取分类讨论.

3 用于求解图形中的线段长度

例6一张直角三角形纸张ABC，∠C=90°，AB=10，AC=6，点D为BC边上任意一点，沿着过点D的直线折叠，使得点C落在斜边AB上的点E上，若当△BDE为直角三角形时，CD的长为____.

图2 图3

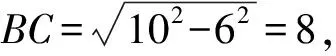
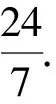
反思遇到几何中的折叠问题时应冷静分析，保证考虑问题的全面性.必要时要画出相关草图辅助分析，求解出满足题干情境的线段长度.

4 用于求解函数图象中点的坐标

例7如图4，已知抛物线y=x2-2x-3的顶点为E，且和x轴正半轴交于点C，在y轴上存在一点D，满足DC=DE，若在直线DE上存在一点P，使得以C、D、P为顶点的三角形和△DOC相似，求出所有可能的点P的坐标.

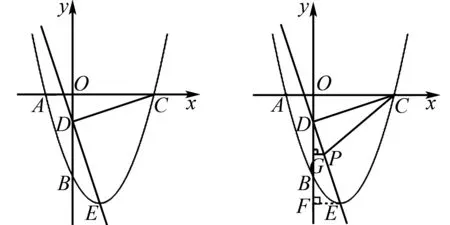
图4 图5

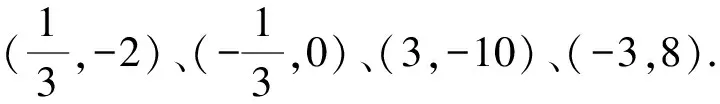
反思求解函数图象中点的坐标问题难度一般较大，解题时应注重联系所学的一次函数图象、二次函数图象、图形的全等与相似等知识点，尤其当对应边不明确时应注重分类讨论.根据图形的全等、相似性质构建相关的等式关系，为求解点的坐标做铺垫.

为使学生掌握应用分类讨论思想解题的技巧，既要注重为学生讲解相关的理论与例题，又要要求学生做好学习的总结，把握不同题型分类讨论的注意事项以及相关细节.同时，要求学生结合自身学习的薄弱点，及时进行针对性的训练，不断提高运用分类讨论思想解题的熟练程度.