基于遗传算法优化BP神经网络的不良路基沉降量预测应用研究

韦周帅，谭 毅，李瑞娇，李运高

(1.广西新发展交通集团有限公司，广西 南宁 530029；2.广西交科集团有限公司 广西 南宁 530007；3.广西北部湾投资集团有限公司钦北高速公路改扩建工程建设指挥部，广西 北海 536000)

0 引言

路基作为道路基础，其沉降幅度直接影响道路的变形与稳定，尤其对软土、红黏土、膨胀土等特殊路基及地基加固工程而言，路基沉降是最重要的性能评价指标。

近年来，人工神经网络因其自组织、自学习与自适应的能力而广泛应用于各个行业的科学研究，其中包括城市道路病害预警及岩土工程领域[1-2]。相对于传统预测方法，如经验公式法[3]、Biot固结理论[4]、FLAC3D、Fluent、Abaqus、COMSOL等基于本构模型进行有限元计算方法[5-6]，BP神经网络算法建模能够更好地利用输入与输出参数相关性，不需要建立土工数值模型进行计算，更易于获得预测值[7]。利用BP神经网络进行路基沉降预测的相关研究较多，但BP神经网络需要大量的不同性质的训练样本，而实际工程中因为考虑监测成本及施工难度等，往往训练样本有限，导致提供的数据样本量不够，应用BP神经网络建模计算结果偏差较大[8-9]。实际上，大多数运营道路能提供的数据多为多年路基沉降值，而依据相关研究，BP神经网络要想达到满意的预测结果，训练样本需要包括多年沉降值、路基路面材料特性、地下水位变化，以及气温、降雨监测等多年观测材料[10]，这大大增加了工程观测成本。

针对以上问题，本文基于遗传优化算法优化BP神经网络，获得遗传优化BP神经网络，进而利用多年路基沉降值预测路基沉降，通过项目工程实测路基沉降数据进行训练及预测，获得准确的遗传优化BP神经网络模型，提高输入参数产出效率。研究成果可以简化训练样本，且保障预测精度，提供更加准确的路基沉降预测手段及预测结果，为工程决策提供可靠依据。

1 方法介绍

1.1 BP神经网络

BP神经网络是一种多层的向前反馈的神经模拟系统，即前馈神经网络，BP神经网络的主要特点体现在其误差反向传播、信号向前传播。在信号从后向前传递的过程中，信号由输入层、隐含层及输出层三层处理，上级神经元只影响临近下级神经元(见图1)。输出层必须得到预期输出，否则信号将反向传递，修正阈值及权值，促使输出层的预测输出值不断接近预期输出值。

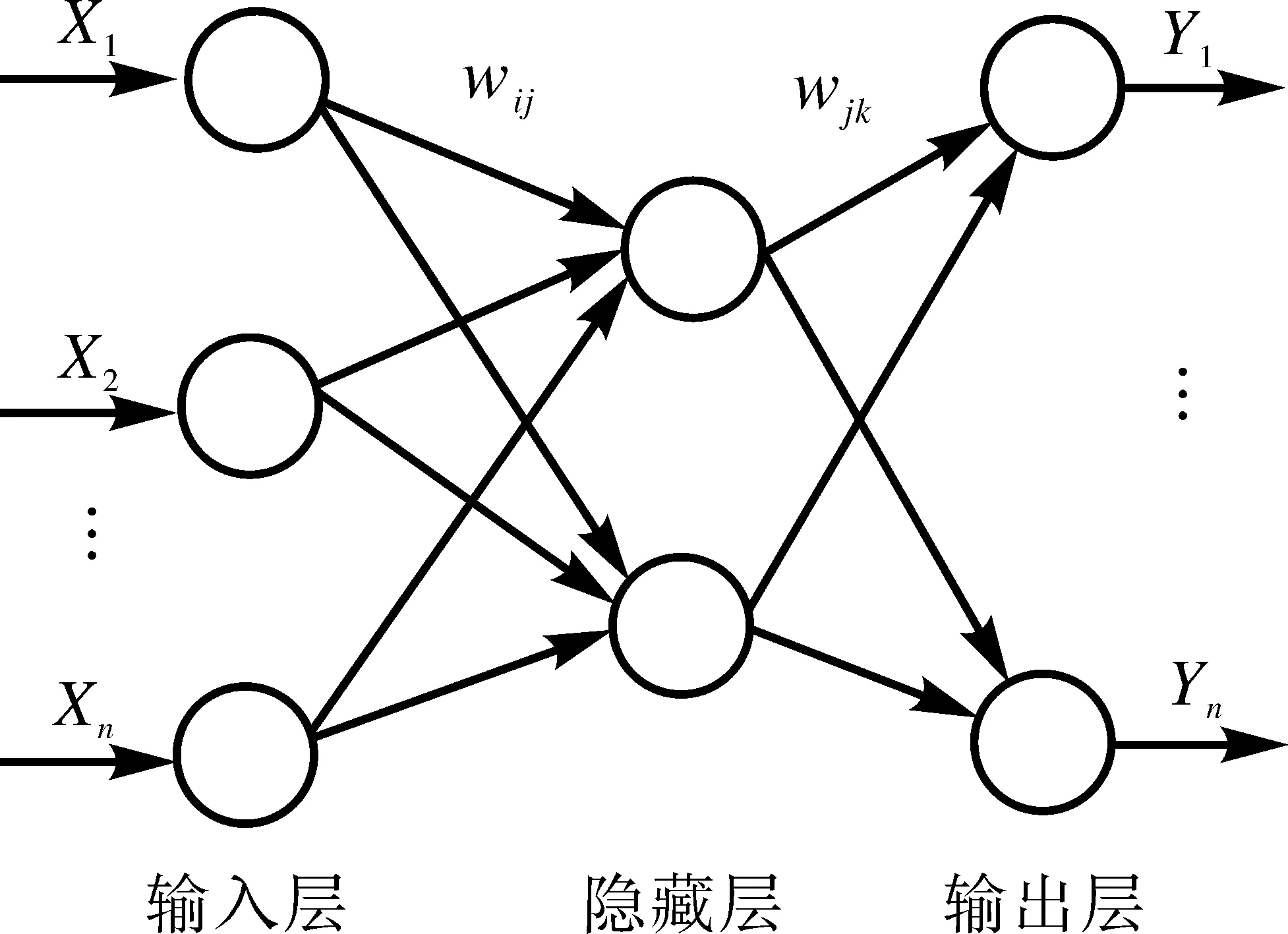
图1 BP神经网络模型拓扑结构图

图1中，X1，X2，X3，…，Xn是输入层的输入值，Y1，Y2，Y3，…，Yn是输出层的输出预测值，wij和wjk为权值。

1.2 遗传算法优化BP神经网络模型

使用遗传优化BP神经网络可以分为三个模块，包括确定BP神经网络的拓扑结构，确定遗传优化参数和BP神经网络的预测模块，流程见下页图2。其中，BP神经网络的确定是指确定BP神经网络输入输出参数个数、输入输出的权值个数，以及隐含层和输出层的阀值个数，根据拓扑结构又可以确定遗传算法的个体长度。优化神经网络的参数是神经网络的权值和阀值，优化算法通过编码把BP神经网络的权值、阀值及遗传算法的输入数据处理为种群，而此种群中每个个体都持有了一个阀值或权值。

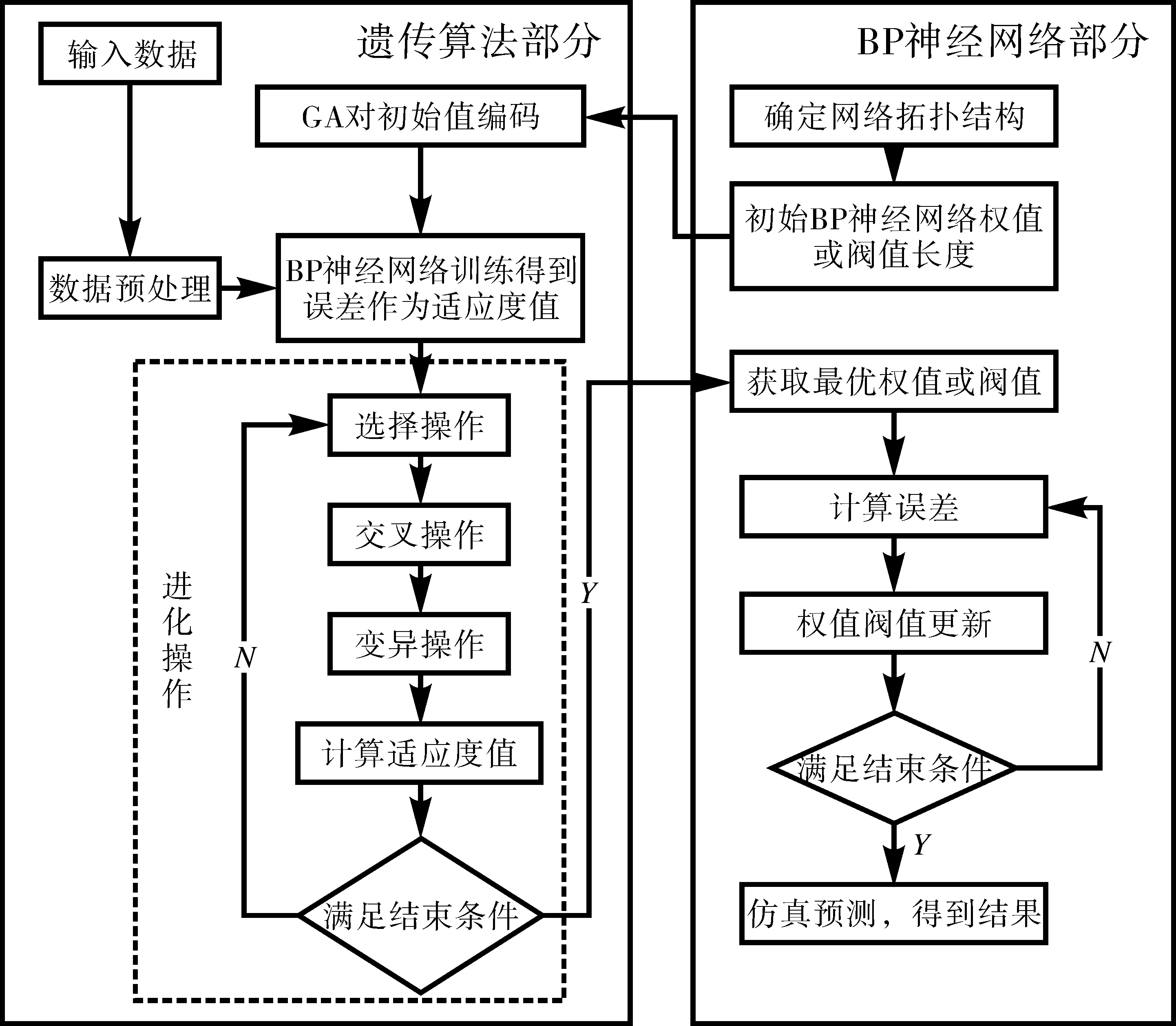
图2 遗传算法优化BP神经网络流程图

1.3 优化要素

遗传优化BP神经网络即利用遗传优化算法优化BP神经网络的初始阀值和权值。根据遗传算法理论，其优化要素按顺序排列包括：(1)种群初始化；(2)适应度函数；(3)选择操作；(4)交叉操作；(5)变异操作。各要素的具体内容可以参见相关文献[11]。

2 路基沉降预测

实测数据取自某公路两幅不同位置的S1、S2通道断面，该项目为软土路基加固工程。其中S1监测断面数据22个，S2监测断面数据21个，分别源自处治后两年内的不定期监测数据。本案例基于Matlab实现计算，依据实测数据，建立模型的输入输出数据，即从已知的数据中一次取5个不同时刻的实测沉降值，用前4个时刻的数据作为网络输入值，后1个做网络的输出值。这样S1和S2就分别得到了时距不等长的18组学习(训练)样本和17组学习(训练)样本，见表1。通过数据的预处理，预测模型有4个输入参数，1个输出参数，隐含层节点数为9。所以设置神经网络的结构为4-9-1，即输入层有4个节点，隐含层有9个节点，输出层有1个节点；共有45个权值，10阀值。如此，用S1时距不等长的前15组作为训练数据，后3组作为测试数据；用S2时距不等长的前14组作为训练数据，后3组作为测试数据；通过遗传优化的BP神经网络计算预测，把训练数据预测的误差绝对值作为测试个体的适应度值，选用适应度值最小的个体进行预测计算。

3 结果分析

3.1 S1通道监测断面预测结果分析

优化过程中，进化次数设置为20，种群规模设置为10，交叉极高率设置为0.2，变异概率设置为0.1；设置迭代次数1 000次，但是迭代7次就达到了设置的收敛目标0.000 1；学习率设置为0.1。遗传优化的适应度曲线见图3。由图3可知，遗传算法优化构成中，当进化代数达到10次后，平均适应度值就已经达到稳定，说明选择进化20次是满足进化要求的。

表1 不等时距学习(训练)样本数据统计表

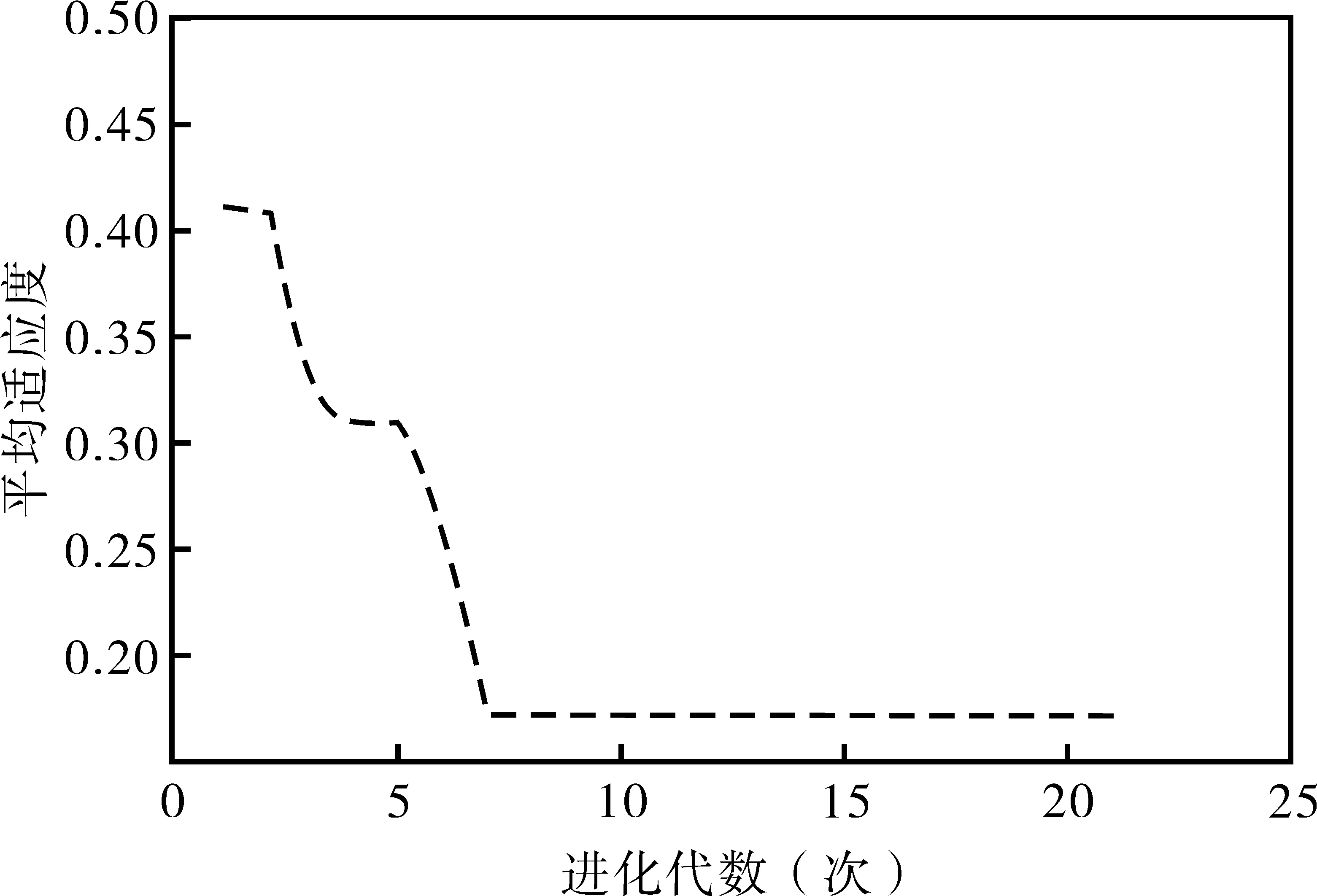
图3 S1通道监测断面神经网络适应度曲线图

S1通道监测断面的预测结果见表2。模型输出选择预测时间分别为448 d、513 d、616 d、693 d，由表2可知，S1通道监测断面路基沉降值的预测值与实际值偏差不大，相对误差分布在1.03%～5.61%，最大达到17 mm，相对误差为5.61%，说明预测结果是可靠的。

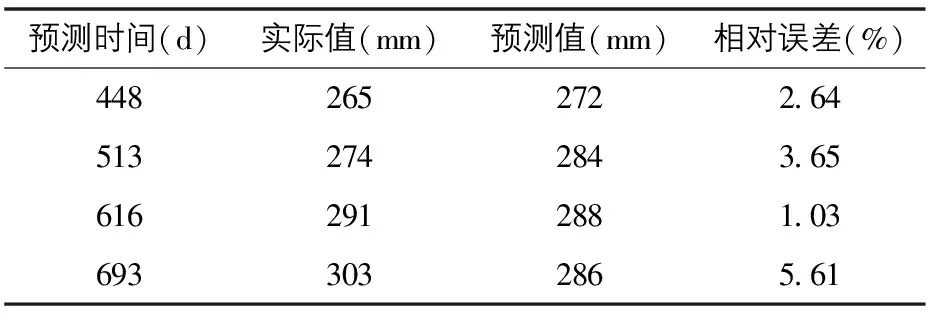
表2 S1通道监测断面预测结果表

3.2 S2通道监测断面预测结果分析

模型参数设置同S1通道监测断面的路基沉降预测模型，程序的遗传优化适应度曲线见图4。由图4可知，遗传算法优化构成中，当进化代数达到15次后，平均适应度值就已经达到稳定，说明选择进化20次是满足进化要求的。

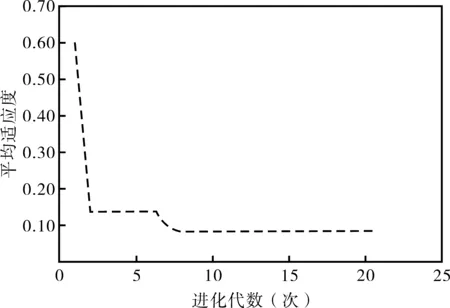
图4 S2通道监测断面神经网络适应度曲线图

S2通道监测断面的预测结果见表3。模型输出选择预测时间分别为451 d、516 d、619 d、696 d，由表3可知，S2通道监测断面路基沉降值的预测值与实际值偏差也不大，相对误差分布在2.36%～3.69%，最大达到16 mm，相对误差为3.69%，说明预测结果可靠。

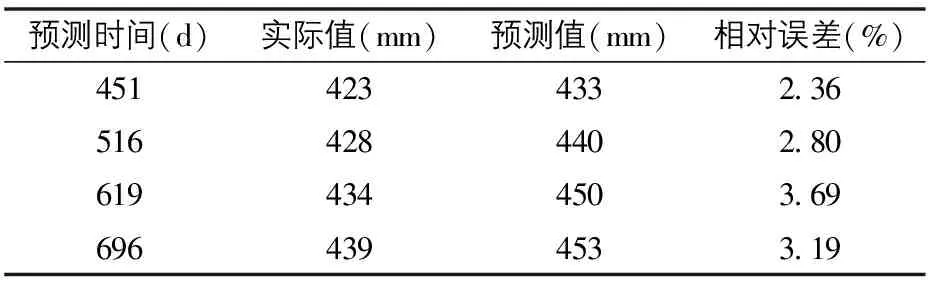
表3 S2通道监测断面预测结果表

3.3 适用性评估

(1)通过两个不同位置通道监测断面的沉降预测结果对比可知，预测结果与实际检测的数值绝对误差约为3～17 mm，相对误差可以控制在6%之内，符合使用要求，证明了此种方法预测路基沉降的可行性。

(2)本研究中S1、S2通道监测断面的沉降实际数据检测并非严格采取相同的时间间隔测定，这种不规律为本模型对未来将要发生的路基沉降预测时间节点造成了一定的难度，间接地提高了数据的样本需求量。

(3)S1、S2两个通道监测断面的神经网络模型的预测值与实际值误差的规律略有不同。S2的模型预测值普遍高于实际值，相对误差变异系数为0.188，S1的模型预测值存在着小于或大于实际值的情况，相对误差变异系数为0.593。这种结果与两个通道监测断面的数据分布规律有关，可通过神经网络模型中不同的模型参数设置进行优化，如隐含层层数及节点数。

(4)BP神经网络的特点是具有学习性和迭代性，数据数量越多，其结果越准确，是当前基础设施大数据应用研究的核心方法。因此，通过加密监测段的数据采集频率，提高数据样本量，并实现长期的数据库更新，是提高其精度的有效方法。

综上所述，相对于多元素下路基沉降的理论分析，基于遗传算法优化的BP神经网络对于路基沉降的预测方法适用性更好，主要体现在原理简单、结果准确、可实现自我学习更新、实用性强等特点。

4 结语

在路基沉降预测方面，为了减少输入参数，保障路基沉降预测精度，本文应用遗传算法优化了BP神经网络，并基于遗传优化BP神经网络，结合某公路不同位置两个通道监测断面的路基沉降数据进行了模型训练及预测。结果表明：简化输入参数的优化BP神经网络，在只将实际工程前期监测的沉降值作为训练样本输入的情况下，进化20次以内即可准确预测路基沉降量，预测误差可控制在6%以内，体现了该方法的可行性。相对于多元素下路基沉降的理论分析，基于遗传算法优化的BP神经网络对于路基沉降的预测方法适用性更好，可用于不良土路基及地基加固工程的长期变形预测和效果评价，其原理简单、结果准确、可实现自我学习更新、实用性强等特点，为今后基础设施状态评估提供了广阔的应用空间。