锚杆布设方式及长度对边坡稳定性的影响分析

2022-08-01陈云生苏初明

西部交通科技 2022年5期

陈云生，苏初明

(广西交通设计集团有限公司，广西南宁 530029)

0 引言

锚杆作为边坡防护最常见的手段，被广泛使用[1]。但近年来，锚杆加固边坡呈现的问题日渐增多，如锚杆拉断、拔出导致的边坡失稳，或过度使用导致的资源浪费等，因此有必要对锚杆的布设方式及长度进行研究。国内有部分学者已对此进行了一些研究，许宇明等[2]以高速公路某路堑边坡为例，研究了锚固长度、锚固角对边坡稳定性的影响；张期树等[3]借助FLAC3D计算软件建立了边坡理论计算模型，研究了锚杆长度、锚固角及锚固位置对边坡稳定性及滑动面的影响；黎海滨等[4]利用离散元软件UDEC建模，研究了锚杆间距、锚杆长度、锚固布设方式等对边坡稳定性的影响规律；安彩龙等[5]借助导数法和Matlab软件中的fmincon函数对锚固角进行了优化，推导了最优锚固方向角计算方法。

为了进一步确定锚杆长度、分布位置、锚杆入射角对边坡稳定性的影响及其规律，本文在查阅资料的基础上，利用Midas NX软件建立计算模型，采用FLAC3D软件强度折减法计算边坡稳定性系数，总结了边坡稳定性变化规律，为工程建设提供参考。

1 计算模型

1.1 岩土模型

本文选用的模型如图1所示。模型长158 m，高100 m，其中边坡高度为60 m，按1∶1放坡，每10 m一级，各级边坡间设置2 m宽平台。土体建模采用Brick和Wedge两种网格类型，整个模型单元数(zones)为4 226，节点数(grid-points)为6 779，离边坡面的网格要比其他网格密。

图1 边坡计算模型图

1.2 结构单元模型

锚杆采用cable单元模拟，由几何参数、材料参数和水泥特性来定义。Cable构件是由两个节点的位置来定义的局部坐标系统，如图2所示。其重心轴与x轴一致，规定节点1指向节点2的方向为x轴，y轴与不平行局部x轴的全局y轴或全局x轴在横截面上的投影对齐。当岩土体受力时，通过变形将力传递到水泥浆上，再传递到节点上，节点的变形使Cable单元产生力学行为，进而约束岩土体变形，实现力学平衡。

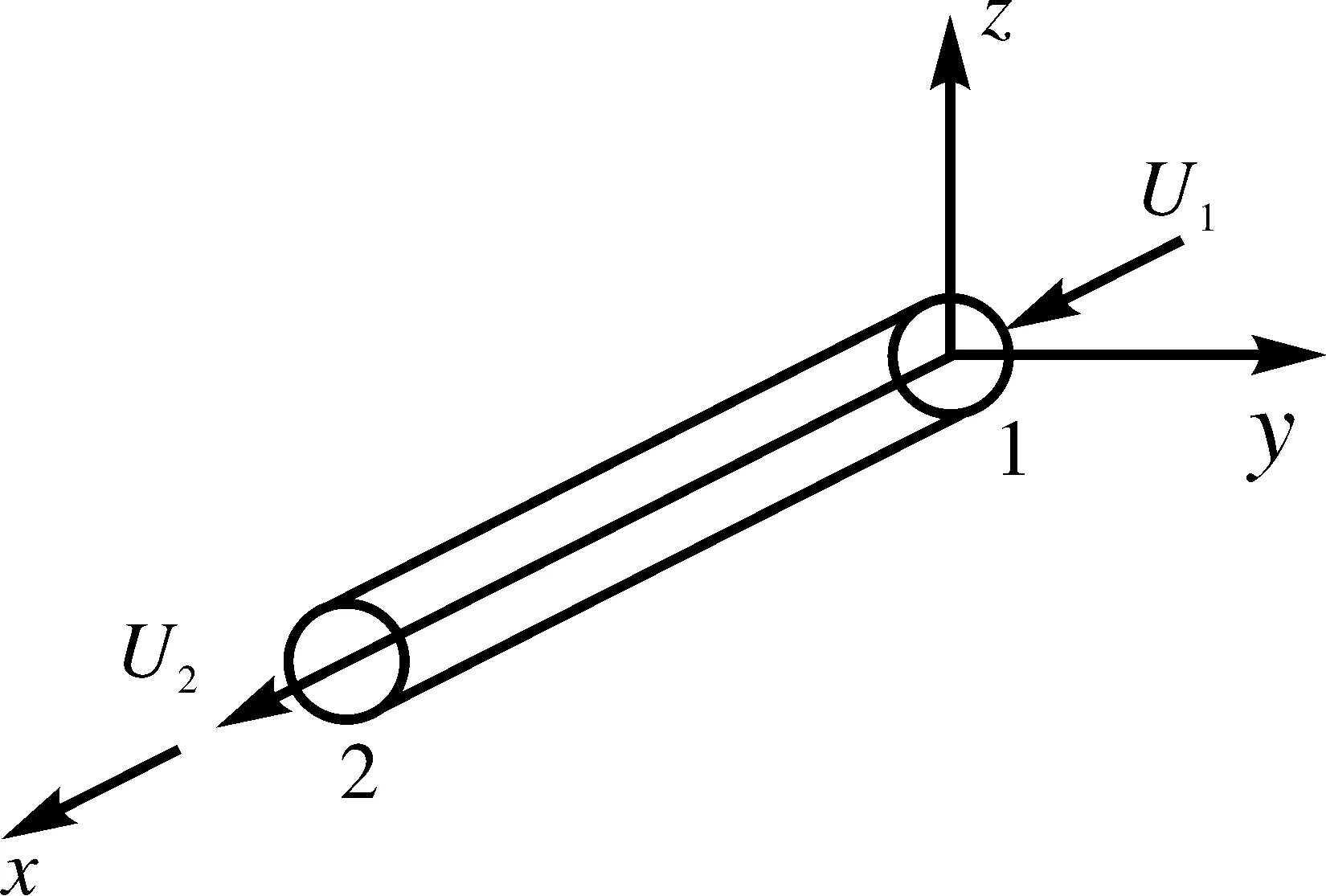
图2 Cable构件的坐标系统及两个自由度示意图

图3 Cable构件材料性能示意图

FLAC3D软件中用一维本构模型来描述轴向特性，如图3所示。超过弹性段(斜线段)轴力不再增加，轴向刚度变为0，单元可随意伸缩，斜线段对应的公式如下：

K=AE/L

(1)

式中：K——轴向刚度；

A——加固横截面；

E——弹性模量；

L——构件长度。

锚杆与土层的接触面具有粘结性和自然摩擦，可以采用弹簧-滑块来形象地描述系统，如图4所示，通过弹簧来模拟锚杆的抗剪力，通过滑块来模拟锚杆的抗拔力。

假定水泥浆为理想弹塑性体，水泥浆内部任意点相对剪切变形为us，则抗剪力Ft、抗拔力Fb、水泥浆剪切刚度kg、水泥浆粘结强度cg之间的关系为：

Ft=kgus

(2)

Fb=cgus

(3)

图4 Cable构件的力学模型图

1.3 边界条件及物理力学参数

边界条件利用FLAC3D软件中的fix及range命令设置。本模型边界条件为：x=0、y=0、x=158 m、y=10 m。界面设置法向约束，下边界约束x、y、z方向位移，上边界设置为自由边界。计算采用摩尔-库仑强度准则，计算参数如表1、表2所示。

表1 土层物理力学参数表

表2 锚杆设计参数表

2 计算结果

2.1 等长锚杆条件下锚固位置及入射角对边坡稳定性的影响

假定锚杆长30 m，自由段长度为18 m，锚固段长度为12 m，单根锚杆预应力取450 kN，锚杆入射角从5°～60°按5°逐步递增。锚固级数选取4种情况：情况1为仅设置一级锚杆，设置位置分别位于第一～六级等六种工况；情况2为设置连续两级锚杆，设置位置位于第一～二级、第二～三级、第三～四级、第四～五级、第五～六级等五种工况；情况3为设置连续3级锚杆，设置位置位于第一～三级、第二～四级、第三～五级、第四～六级等四种工况；情况4为设置连续四级锚杆，设置位置位于第一～四级、第二～五级、第三～六级等三种工况。各种情况的计算结果如图5所示。

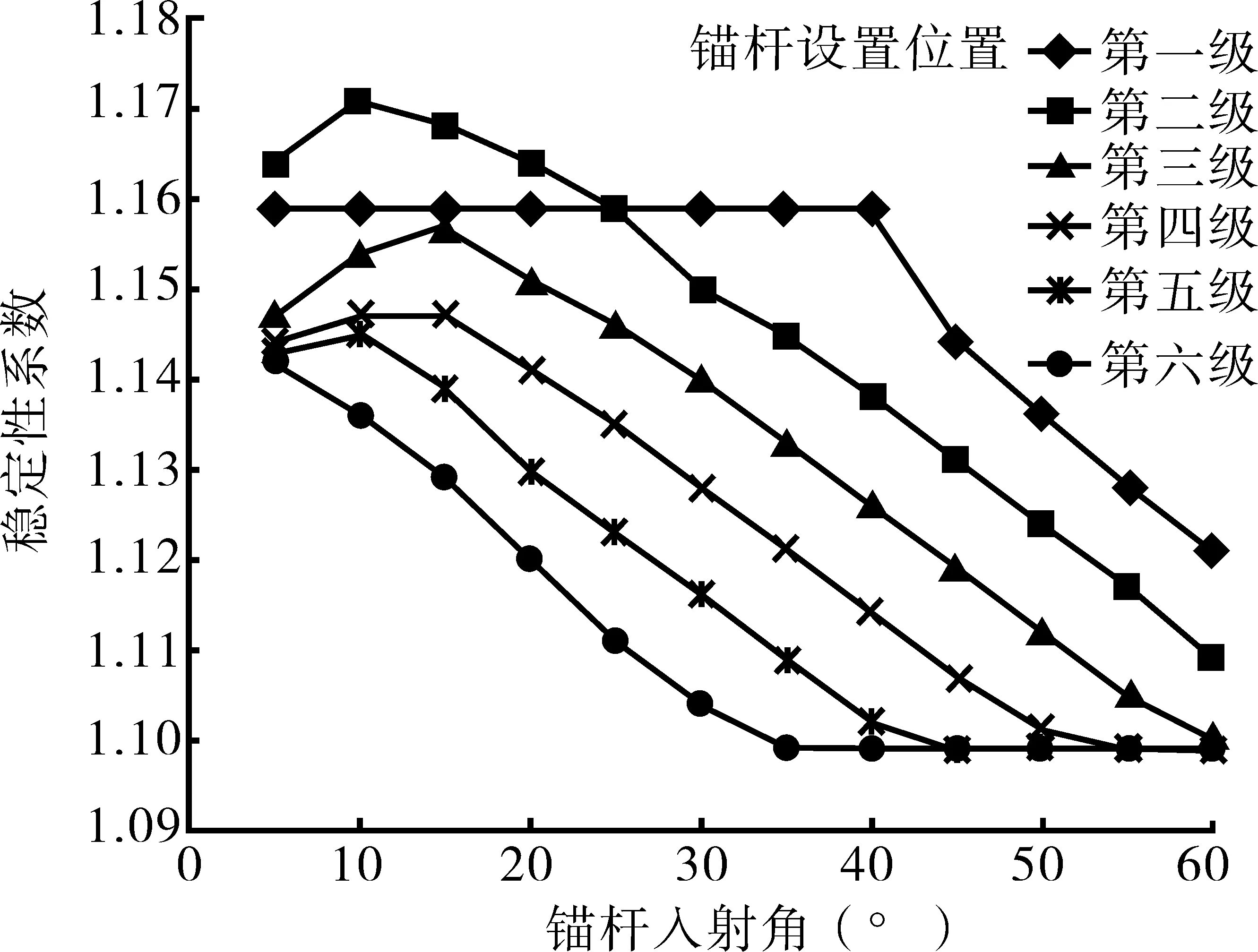
(a)仅设置一级锚杆

(b)设置连续两级锚杆

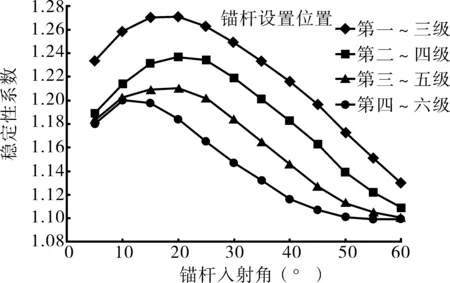
(c)设置连续三级锚杆

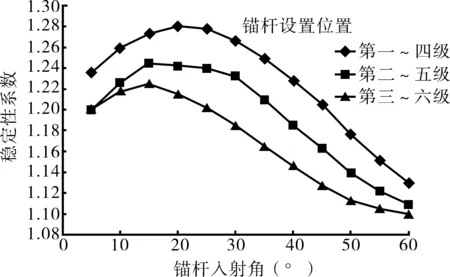
(d)设置连续四级锚杆

由图5计算结果可知，随着锚杆入射角的增大，边坡稳定性系数整体上呈现先增大后减小最终趋于稳定的趋势，边坡稳定性在5°～25°达到最大，锚杆入射角存在最优值，且实际工程中不宜采用过陡的入射角。由图5(a)～(b)可知，边坡第一级或第一～二级设置锚杆后的稳定性在锚杆入射角≤40°或≤35°的工况下相同，这是因为当锚杆入射角较小时，滑动面剪出口高于锚杆顶部，此时稳定性系数不受锚杆影响；当锚杆入射角较大时，滑动面穿越锚杆从第一级坡脚剪出，稳定性将受锚杆入射角影响。

最优锚杆入射角受锚固位置影响，坡脚及坡顶锚杆的最优入射角小于中部锚杆。锚杆入射角及锚杆长度固定的情况下，锚杆设置在坡脚的稳定性最大，其次为中部，设置在坡顶最小。在实际工程中，应重视坡脚加固，且坡脚不宜采用短锚杆，加固坡脚可迅速提高边坡稳定性，其次为边坡中部“壮腰”，仅加固顶部对提高稳定性作用甚微。

2.2 非等长锚杆条件下分布方式对边坡稳定性的影响

采用3种长度的锚杆，分别为30 m、20 m、12 m，锚固段均为12 m，锚杆入射角均为15°，从坡脚至坡顶依次选取“长(30 m)-中(20 m)-短(12 m)”；“长(30 m)-短(12 m)-中(20 m)”；“中(20 m)-长(30 m)-短(12 m)”；“中(20 m)-短(12 m)-长(30 m)”；“短(12 m)-长(30 m)-中(20 m)”；“短(12 m)-中(20 m)-长(30 m)”等六种组合类型，计算结果如表3所示。

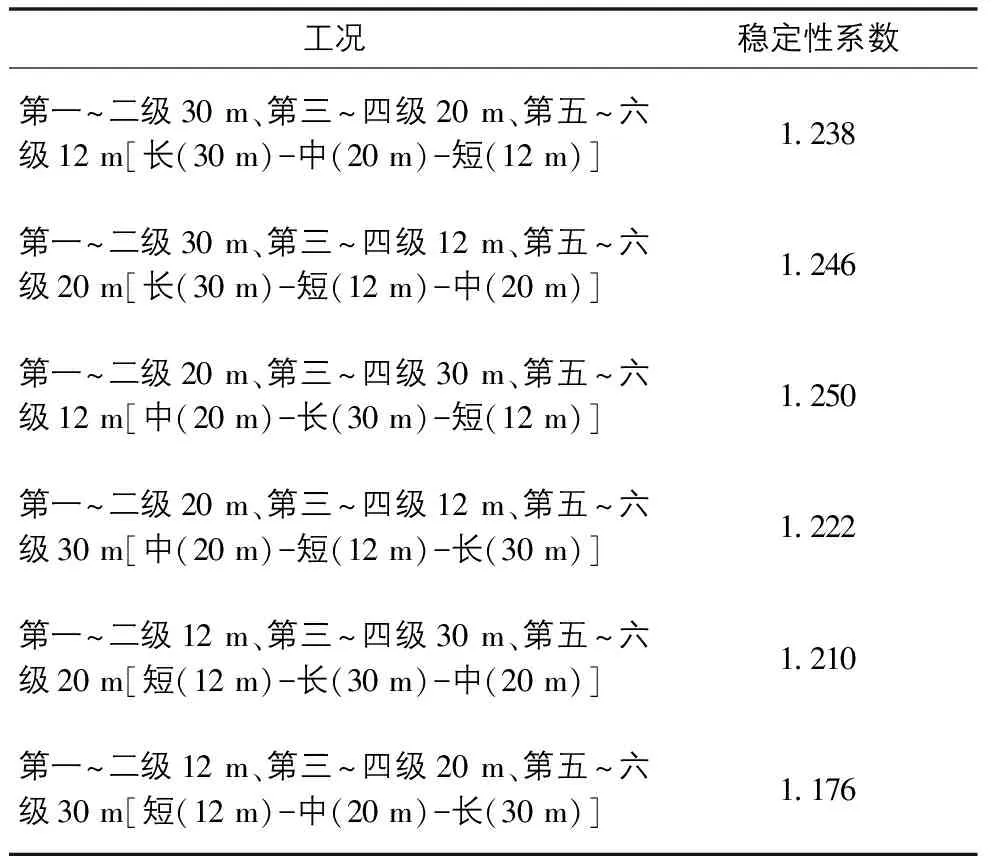
表3 非等长锚杆条件下边坡稳定性系数计算结果表

由表3可知，坡脚设置短锚杆的稳定性系数最低，这是因为锚杆长度偏短，提供的抗拔力小，违背了上节所说的优先加固坡脚的原则。稳定性系数按“长(30 m)-中(20 m)-短(12 m)”的排列方式比“中(20 m)-长(30 m)-短(12 m)”的排列方式低，这是因为坡脚第一、第二级边坡处滑动面离坡面距离短，采用20 m或30 m锚杆的锚固段均能穿过滑动面，故加固效果相同，而第三～四级边坡采用20 m锚杆偏短，部分锚固段未完全进入滑动面以外的岩土体，加固效果不如30 m锚杆。在实际施工中，坡脚应提供足够的抗拔力，但锚杆长度可比中部略短，因此，坡脚可在减短锚杆的基础上采用加密间距的方法来提高边坡稳定性。