一种差分码偏差估计的简化模型及其评估分析

汪奇生

1 湘潭大学土木工程与力学学院，湖南省湘潭市北二环路，411105

在卫星导航定位中，码观测值会因为硬件特性在卫星和接收机端产生硬件延迟，2个频率的码观测值硬件之差称为差分码偏差(differential code bias, DCB)[1-2]，其在卫星端称为卫星差分码偏差，接收机端称为接收机差分码偏差。DCB是电离层建模和精密单点定位中重要的误差源，需要被精确计算。DCB分为频内DCB(同一频率的码观测值硬件延迟之差)和频间DCB(不同频率的码观测值硬件延迟之差)[3]。频内DCB一般可以通过码观测值的平均组合观测值求取，本文所指的DCB为频间DCB。

卫星和接收机DCB的估计方法一般有2种：一种是采用球谐函数进行全球电离层建模，同时估计卫星和接收机DCB[4-6]。首先需要联合全球的测站数据进行观测方程列立，然后估计球谐函数系数和卫星及接收机DCB。该方法估计DCB的效果依赖于建模的精度，并且有一定的计算量。另一种是使用已有的全球电离层图(global ionosphere map, GIM)。首先进行时间和空间上的内插来获取穿刺点的TEC，进而消除其参数，然后估计卫星和接收机的DCB值[7-9]。该方法可在一定程度上减少计算量、提高估计效率，但其估计DCB的效果主要依赖于GIM精度。

由于2种常规方法都需要进行电离层建模和使用已有的GIM信息，因此本文在原有方法的基础上提出一种差分码偏差估计的简化模型，将测站方向上各穿刺点的VTEC简化为一个参数，分时段进行直接估计。为验证该方法的有效性，采用球谐函数建模和基于GIM的估计方法进行比较分析。选用2016-01近200个IGS测站的GPS+GLONASS数据进行实验，并采用CODE提供的产品进行验证。实验结果验证了本文方法的有效性。

1 差分码偏差估计方法

1.1 电离层TEC观测值

GPS和GLONASS 的伪距和载波相位观测值可以表示为[10]：

(1)

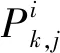
一般情况下，采用载波相位平滑伪距法来提取电离层延迟：

cDCBi+cDCBj

(2)

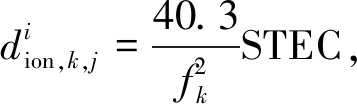
STEC=M(z)·VTEC=

(3)

式中，M(z)为电离层投影函数，R为地球平均半径，H为假设的电离层薄层高度，z为接收机到卫星方向上在假设电离层薄层处的天顶距，α为调节因子(一般取值为0.978 2)。因此，可以将式(2)进一步表示为：

P4,sm=F(f)·M(z)·

VTEC+cDCBi+cDCBj

(4)

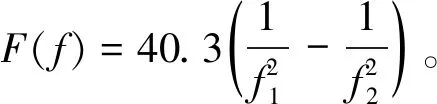
1.2 球谐函数建模求解DCB

本文采用15阶球谐函数进行全球电离层TEC建模，结合式(4)可以将球谐函数建模的观测方程表示为[11]：

F(f)·M(z)+cDCBj+cDCBi=P4,sm

(5)

式中，n和m分别为球谐函数的阶次，β和ms分别为穿刺点的地理纬度和日固经度，anm和bnm分别为模型的待求系数。采用分段线性方法进行球谐函数参数估计，每2 h估计一组参数， 1 d共估计13组参数，则需要估计的球谐函数参数数量为13×256=3 328个。由于使用全球测站的GPS+GLONASS观测值共同建模，因此观测值的个数远大于待求参数的个数，可以直接使用最小二乘平差法求解。需要估计的参数为：

(6)

式中，G和R分别为GPS和GLONASS，r和 i分别为测站和卫星。同时，为分离接收机DCB和卫星DCB，还需要在平差方程中分别对GPS和GLONASS进行卫星DCB零矩阵约束：

(7)

1.3 基于GIM建模求解DCB

不同于球谐函数建模，基于GIM建模可直接使用IGS提供的GIM。本文首先采用CODE的GIM产品进行时间和空间上的内插来获取穿刺点的VTEC值，然后直接消除VTEC参数，其观测方程可以表示为[7]：

cDCBr+cDCBi=

(8)

式中，N为观测值的总数，其他参数意义与前文相同。同时，为分离卫星和接收机DCB的参数，同样需要添加式(7)进行约束。因此，基于GIM建模求解DCB可以直接获取GPS和GLONASS的卫星及接收机DCB值。

1.4 简化模型建模求解DCB

采用球谐函数建模在理论上比较严密，但待估参数较多，计算量较大。因此在求解DCB时，可以采用IGS的GIM产品直接获取VTEC，能减少估计参数、提高解算效率，但解算效果要依赖于GIM的精度。测站方向上的穿刺点在一定范围内的VTEC变化不大，对电离层TEC项进行平均(式(8))。根据这一特点，可以将穿刺点的VTEC在一个时段内简化为一个参数进行估计，从而获取卫星和接收机的DCB值。

根据球谐函数模型和基于GIM模型提出简化模型，假设一定空间范围内的测站穿刺点VTEC在一定时段内不变或变化很小，则可以将一个测站一段时间内(1 d可分为若干个时段，本文采用24个时段)的VTEC值设为一个参数，观测方程为：

cDCBi+cDCBr=P4,sm

(9)

式中，VTECr,t为测站r在t时段内的VTEC均值，即简化后的电离层TEC参数，其他参数意义与前文相同。该模型对穿刺点的VTEC参数进行简化，减少待估参数，可以直接求解DCB值。为分离卫星和接收机DCB参数，同样需要进行式(7)的卫星零均值约束。可以发现，TEC参数简化后模型的可行性决定了简化模型的有效性。但考虑到一定时段内测站方向上各穿刺点的TEC变化较为缓慢，而且简化过程相当于对各穿刺点的TEC进行平均，因此后续实验将进一步分析其估计DCB的效果。

2 实验数据

为评估本文方法的有效性，选取IGS提供的2016-01(doy 001～031)近200个测站的观测值作为实验数据。这些测站在全球均匀分布，但陆地上的测站居多。测站都能接收到GPS信号，其中一部分还能接收到GLONASS信号。为更好地评估和分析本文方法的有效性，分别采用球谐函数建模(SHM)、基于GIM建模(DGM)和本文提出的简化模型建模(DSM)3种方法估计GPS和GLONASS的P1-P2卫星和接收机的DCB，同时采用CODE提供的GPS和GLONASS的P1-P2 DCB产品进行验证和分析。评估分析实验策略如表1所示。

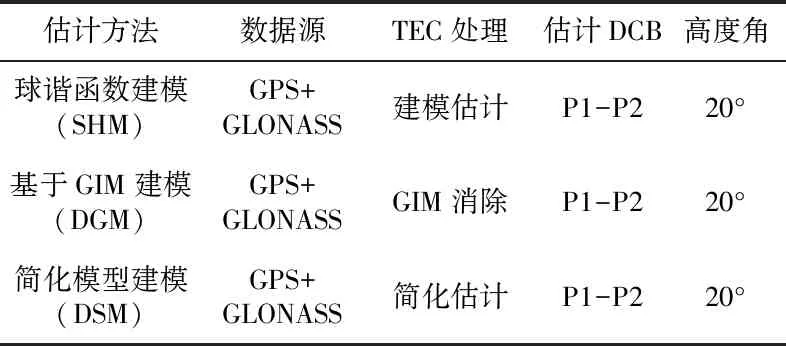
表1 评估分析实验策略

3 结果讨论与分析

3.1 卫星DCB估计结果

为更好地分析本文方法估计的DCB效果，选择CODE提供的GPS和GLONASS的DCB产品作为参考，比较分析3种方法估计的卫星DCB精度，分别如图1(GPS卫星按照类型排列)和图2(GLONASS卫星按照频率排列)所示。

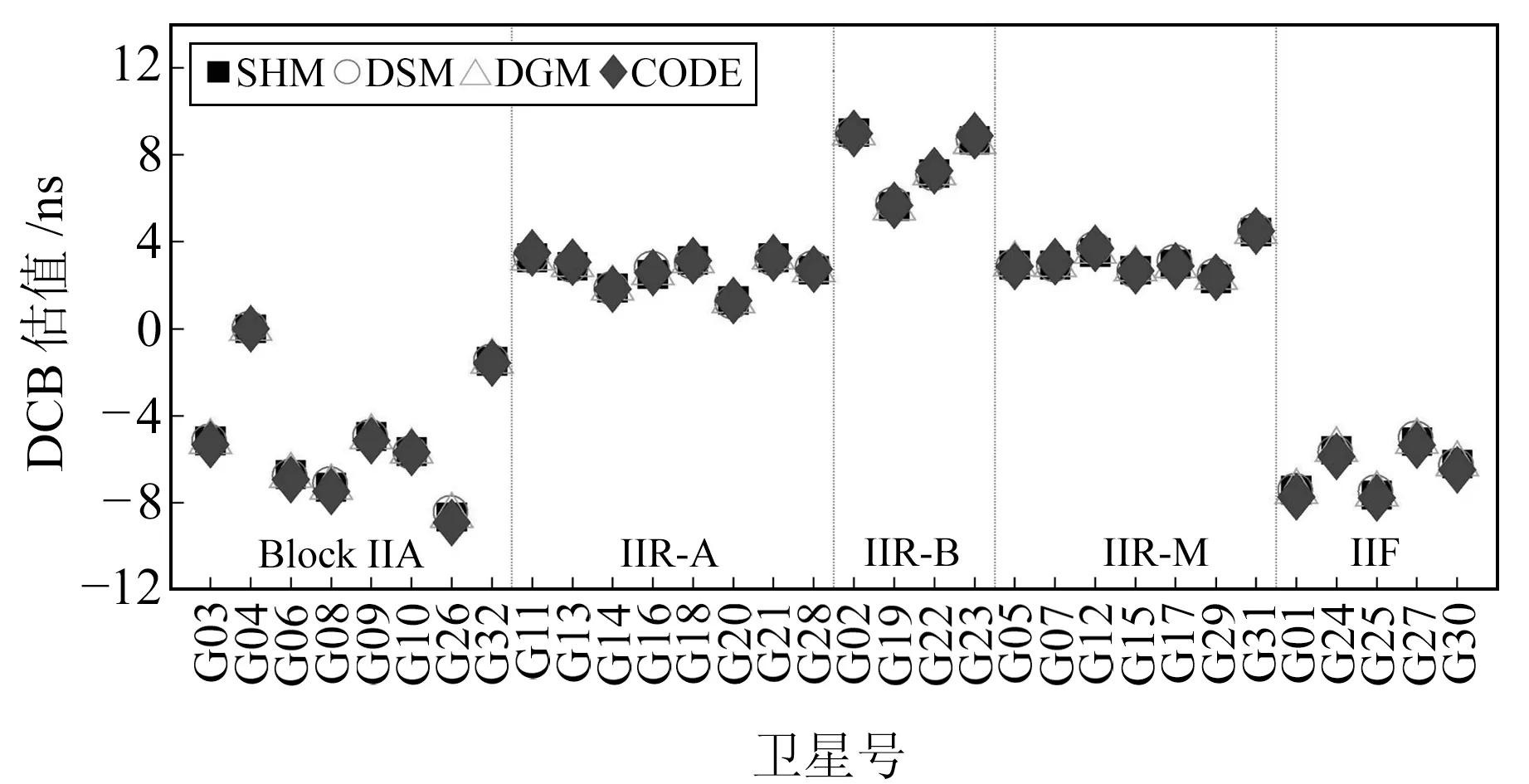
图1 GPS卫星P1-P2 DCB估值

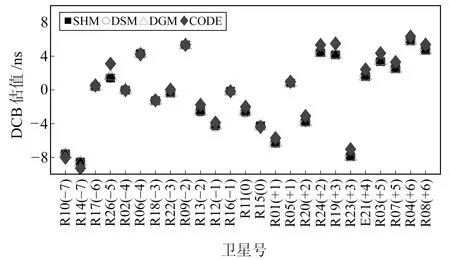
图2 GLONASS卫星P1-P2 DCB估值

由图1可见，GPS卫星DCB月均值为-10～10 ns，3种方法估计的结果与CODE值非常接近，且相同类型卫星的DCB值较为接近，说明DCB主要与硬件设备有关。由图2可见，GLNASS卫星的DCB估值为-10～7 ns，且比较分散。不同于GPS，各种方法的估计值在一些GLONASS卫星上有一定的差异，这是因为GLONASS卫星采用的是频分多址技术，该技术对其卫星DCB估值有一定的影响。

为进一步分析3种方法在估计GPS和GLONASS卫星DCB上的精度，以CODE提供的产品为参考，统计3种方法估计的卫星DCB值的平均偏差(bias)和标准差(STD)，分别如图3和图4所示。

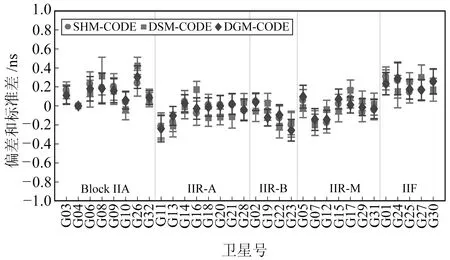
图3 GPS卫星P1-P2 DCB 偏差和标准差

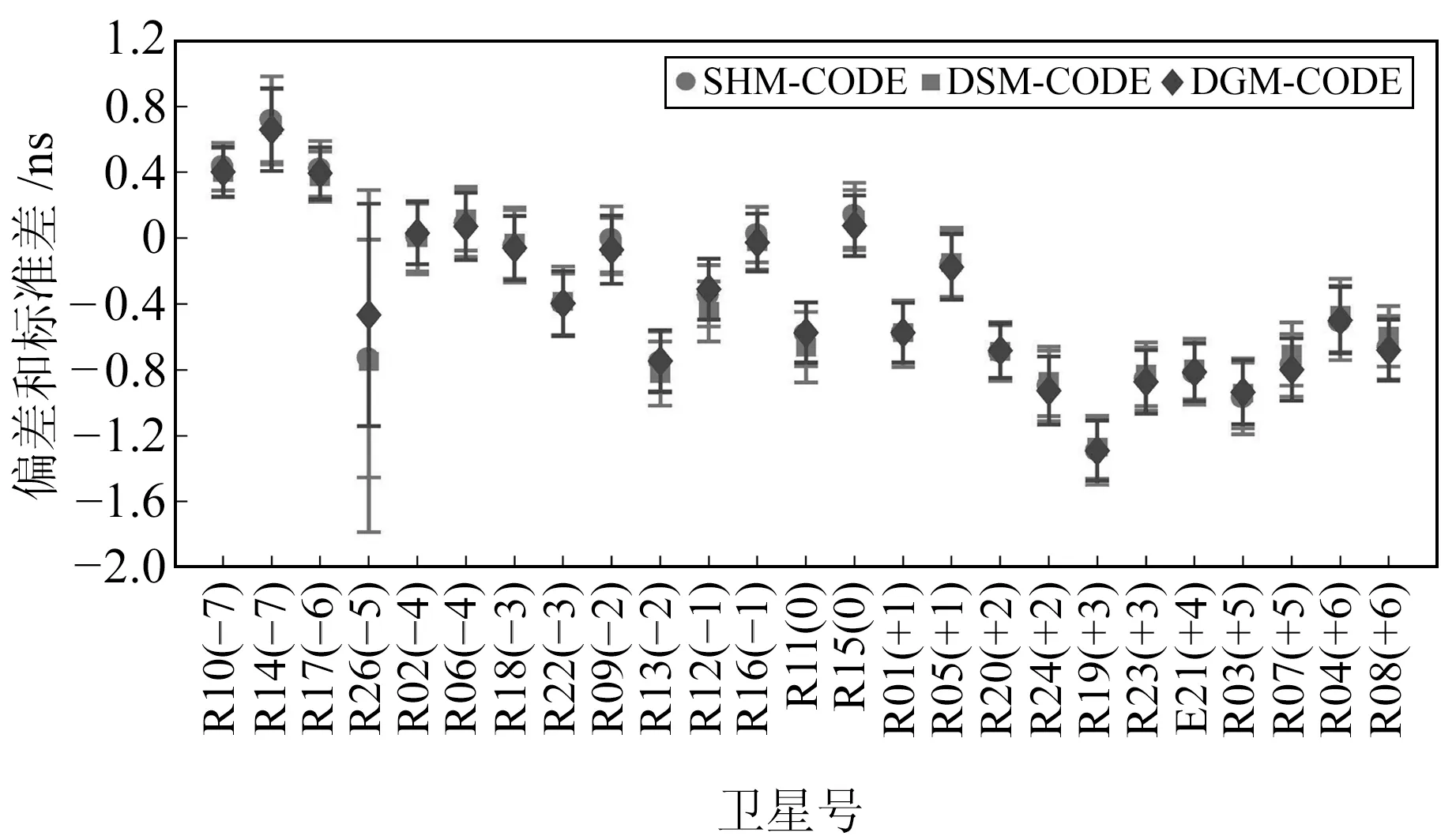
图4 GLONASS卫星P1-P2 DCB 偏差和标准差

由图3可见，3种方法估计的GPS卫星DCB值与CODE产品相比，平均偏差为-0.3～0.5 ns，标准差为0.05～0.20 ns，说明3种方法的估计值与CODE产品有较好的一致性。相比于本文DSM方法，采用SHM和DGM方法估计的结果偏差更小，这是因为SHM与CODE都是采用球谐函数进行建模，DGM则直接使用CODE提供的GIM产品。而本文采用简化模型提高估计效率，观测数量较少的部分卫星可能影响其估值精度，但精度值也达到0.2 ns。由图4可以看出，相比于GPS，GLONASS卫星3种方法的估计值与CODE产品的偏差比较分散，偏差为-1.3～0.7 ns，标准差为0.14～1.10 ns，这可能与GLONASS卫星采用的频分多址技术有关。其中，R26卫星的偏差最大，这可能与其较少的观测卫星数量有关。对比3种方法可知，本文方法相对于CODE的偏差和标准差还是比较接近的，说明本文方法能达到与SHM和DSM方法相同的估计效果。

3.2 接收机DCB估计结果

与卫星DCB不同，接收机DCB除了与本身的硬件特性有关外，还与接收机类型、天线类型和接收机所处位置有关。为更好地比较分析GPS和GLONASS接收机DCB的估值效果，分别从观测数据中选择具有不同接收机类型的30个测站用于比较分析。表2、表3分别为30个GPS和GLONASS跟踪站的信息。图5和图6分别为3种方法和来自CODE产品的GPS和GLONASS 30个测站的接收机DCB值。图中测站按照不同的接收机类型排列，不同接收机类型用虚线划分。

表2 GPS 跟踪站信息

由图5可见，GPS接收机DCB的月均值为-20～15 ns，3种方法解算的结果与CODE产品比较接近。同时，相同接收机类型的DCB月均值比较接近，但也会因天线类型的不同而产生波动，说明接收机DCB的值与接收机和天线类型均有关，但接收机DCB的稳定性还需要考虑地理纬度效应。图6中GLONASS接收机DCB月均值为-30～20 ns，3种方法解算的结果比较接近。相同接收机类型的DCB月均值也比较接近，接收机类型、天线类型均相同的DCB值则更为接近。

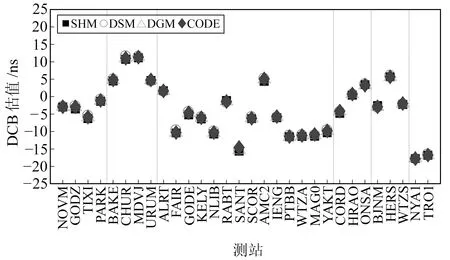
图5 GPS 接收机P1-P2 DCB估值

图6 GLONASS 接收机P1-P2 DCB估值

为进一步评估本文方法估计接收机DCB的效果，以CODE提供的DCB产品为参照，计算3种方法估计的接收机DCB值与CODE提供的DCB产品之间的平均偏差和标准差，如图7和图8所示，图中测站按照其所处的纬度位置排列。

由图7可以看出，3种方法的结果与CODE的平均偏差为-0.6～0.7 ns，标准差为0.05～0.7 ns。其中DGM的偏差和标准差最小，说明电离层精度与接收机DCB的相关性最强。从测站纬度分布可以看出，电离层活跃程度与接收机DCB的估计结果有关。DSM简化模型偏差较大，说明简化估计VTEC带来的误差会影响接收机DCB的估计结果。

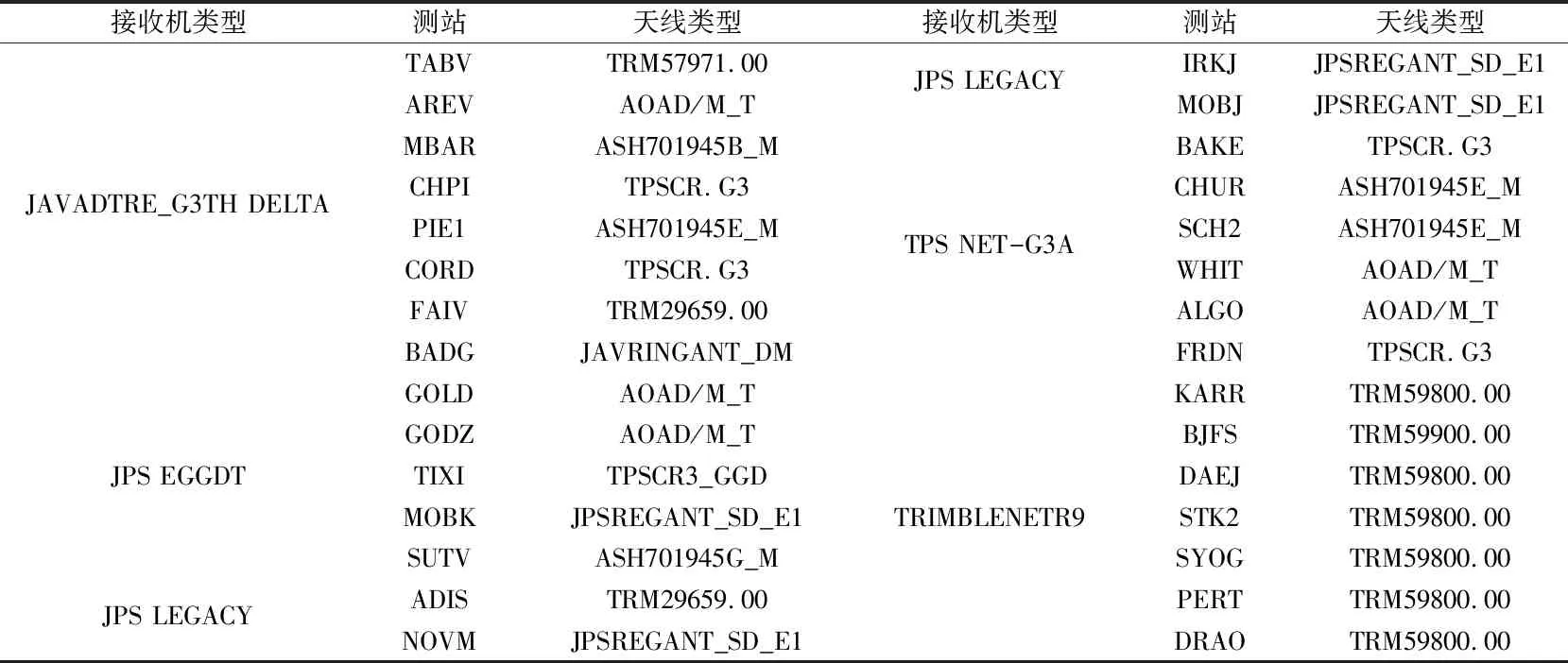
表3 GLONASS 跟踪站信息

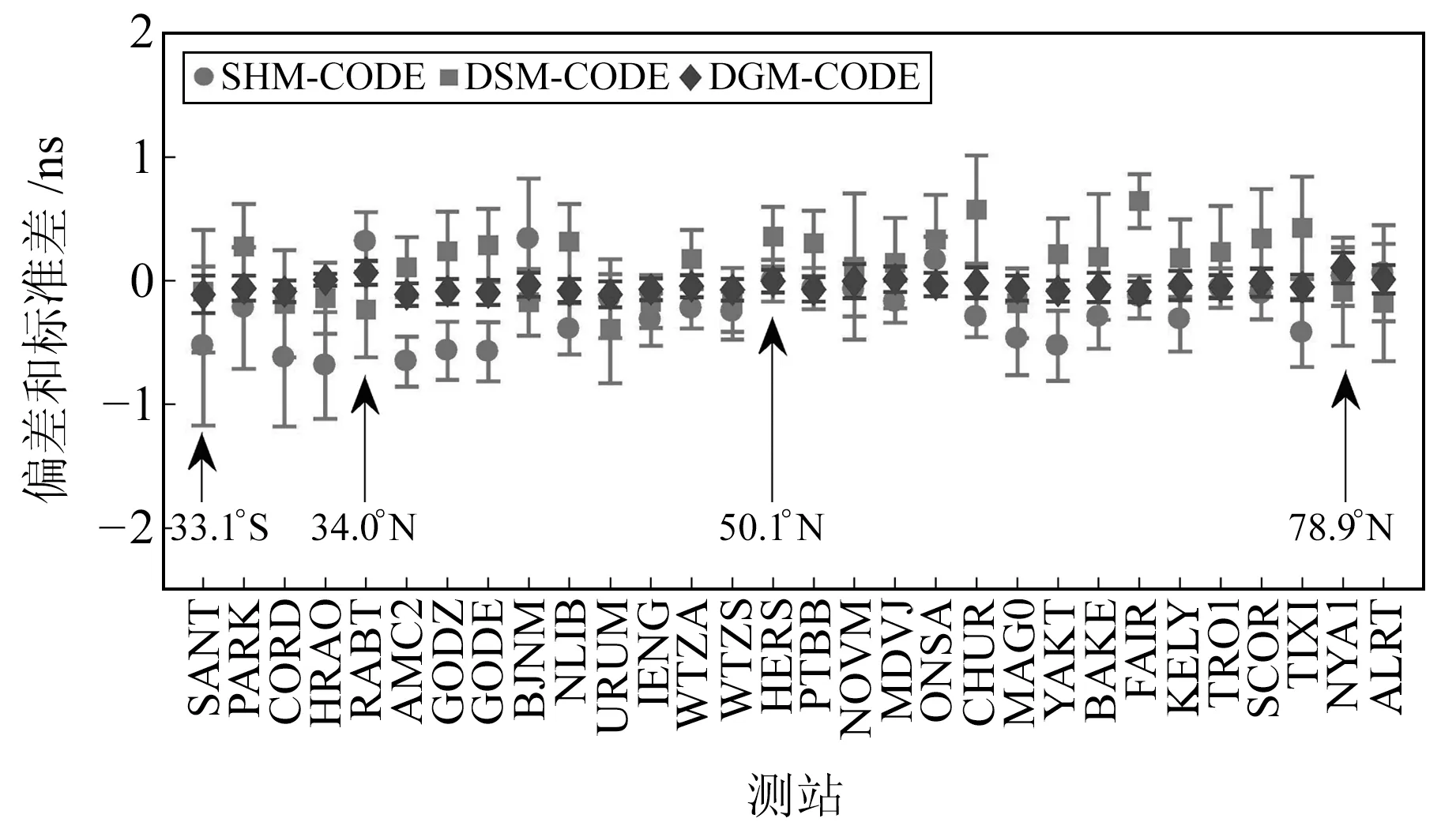
图7 GPS 接收机 P1-P2 DCB平均偏差和标准差

图8 GLONASS 接收机 P1-P2 DCB平均偏差和标准差

由图8可见，3种方法的结果与CODE的平均偏差为-1.5～1.5 ns，标准差为0.16～1.2 ns。GLONASS接收机估计偏差较大，可能与其卫星采用的频率技术有关；简化模型的偏差较大，说明简化VTEC估计带来的电离层误差会影响接收机DCB；低纬度分布的接收机DCB偏差较大，说明其受到电离层纬度效应的影响。

4 结 语

1)对于GPS和GLONASS卫星DCB，本文方法与其他2种方法的估计结果比较接近，且GPS和GLONASS卫星DCB与CODE产品相比的平均偏差分别为-0.3～0.5 ns、-1.3～0.7 ns，标准差分别为0.05～0.20 ns、0.14～1.10 ns。

2)对于接收机DCB，3种方法与CODE产品的平均偏差分别为-0.6～0.7 ns (GPS)和-1.5～1.5 ns (GLONASS)。

实验结果验证了改进方法的有效性。需要说明的是，本文实验是在太阳活动相对平稳的条件下进行的，太阳活动剧烈条件下该方法的适应性还需进一步探讨分析。