张量分解理论下的10 kV配电网电压数据修复方法

王晓虎

（上海电机学院电气学院，上海 201306）

完整准确的10 kV配电网运行数据是负荷侧线变关系、故障定位、偷电用户监测等关键应用技术的基础[1-2]。但是现实场景中由于受到了人为故障、通讯中断、计量设备故障等原因的影响，10 kV配电网运行数据的完整度很难保障，为此就需要使用算法进行数据的有效修复[3]。除此之外，在建设智能电网的国家战略下，各种负荷侧的监测计量设备会产生海量数据，对原始数据的有效修复是高质量使用这些数据的首要前提。

目前相关学者针对10 kV配电网运行数据修复这一课题的解决方法主要集中在专家规则修复方法、训练数据模型的修复方法和插值修复方法。首先，基于专家规则的修复方法是利用数据之间的物理关联性进行数据修复，文献[4]提出充分利用采集设备的多重冗余配置，加权处理修复数据。其次，构建训练数据模型进行数据修复的方法主要依靠时间序列模型和神经网络模型来搭建，通过预测缺值来修复数据。文献[5]通过构建基于随机森林的时间序列模型来进行数据修复；文献[6]通过Koho⁃nen网络对日负荷曲线进行聚类，产生各类的特征曲线，使用特征曲线修复数据；文献[7]通过模糊软聚类思想对Khoonen神经网络进行了改进用以修复缺失数据；文献[8]基于次序属性找到原始数据内包含的有效特征，依次训练模型进行数据修复。最后，插值的修复方法主要是根据缺失值周围数据进行缺失值修复，其中较为典型的是基于矩阵的插补方法，矩阵的插补方法主要是贝叶斯主成分分析方法[9]和概率主成分方法[10]。在插值法中，构建合理的矩阵，使用适当的分解策略是数据修复的关键。文献[11]结合当前用电信息具有时空的关联性，构造时空矩阵，使用矩阵补全算法修复缺失数据。

当前针对配电网的数据修复研究，大部分学者主要利用了配网时序电压变化的内在规律性，忽视了网架拓扑结构间、相似日之间的电压相关性。其次，当前传统的数据修复方法对数据依赖度较高，对于缺失数据量较大的数据集修复效果不佳。

为解决这些不足，本文基于三维的张量（ten⁃sor）理论，首先定义了用电数据的时空张量，从而充分利用网架拓扑结构之间、相似日之间的电压联系；最后利用张量分解理论进行数据修复，这样既利用了数据内在的耦合关系，又能够有效提高缺失数据量较大数据集的修复精度。本文基于某地实际系统中导出的10 kV配电网络电压数据对所提方法进行验证，结果显示在不同数据缺失比例下，可以有效的对缺失数据进行修复。

1 10 k V配电网电压数据修复模型

1.1 时空张量的构建

现代意义的张量由沃尔德马尔·福格特在1899年开始使用，即张量是高维数组的统称，如图1所示，0阶张量即通常概念上的标量a，一阶张量等价于矢量a，二阶张量为矩阵A x·y，三阶张量是3维矩阵A x·y·z[12]。

图1 张量维度Fig.1 Tensor dimensionalities

基于此本文提出的时空张量概念是指一张量共包含3个维度，分别是时间序列的时间维度，相似日的时间维度，所属同一供电10 kV母线的空间维度，如图2所示。时间序列的时间维度是指一天之内的电压时序数据u(t)={u(t1),…,u(t m)}；由于相似日的电压时间序列变化具有相似性，本文以一周为相似日间隔选取相似日序列uT={uT1,…,uT n}；同一供电母线的空间维度是指同一10 kV母线下所属多个台区电压数据组成空间维度u j={u j1,…,u j z}。由此构

图2 时空张量的维度Fig.2 Dimensionality of spatio-temporal tensor

成的时空张量为

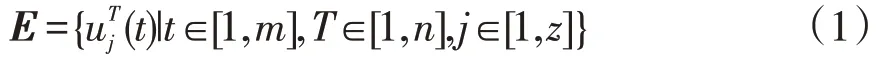
式中：E为时空张量；m为一天之内电压时序数据长度；n为选取相似日数；z为同一母线下台区数。

系统导出的不同台区电压数据常常存在缺失问题[13]，由于这种电压数据是采集计量设备等时间间隔收集的，众多学者选择构建时序数据模型，利用数据内在的关联性修复缺失点位的数据。这种思路是考虑了“时”这一个维度的方法。但是由于电压数据波动具有随机性，这就导致了数据修复时常常效果不够理想。且GIS系统中通常具有相关地区供电系统的拓扑结构信息和较长时间内的数据信息，单一的一个时间维度并不能够利用全部的有效信息。本文所提的时空张量，充分挖掘系统内在的有效信息，利用数据内生的耦合关系进行张量构建。

1.2 基于规则化均值的缺失张量初始化

在对张量进行贝叶斯CP分解时，为提高算法效率需要对缺失数据进行初始化填充。为满足时空张量的修复需要本文特使用规则化均值填充方法。

由于时空张量定义的特殊性，电压数据在各个行列间存在一定的相似性，选择适当的临近数据填充缺失值与真实数据误差较小，可以有效减少运算次数。如图3所示，在时空张量E中位置E(c1,c2,c3)存在缺值式中c1表示时间序列维度，c2表示同一母线维度，c3表示同一相似日序列维度。选择同一相似日下不同台区同一时刻的有效数据集合U1，同一台区同一时刻不同相似日下有效数据集合U2，基于此计算均值填充在时空张量的缺失处。

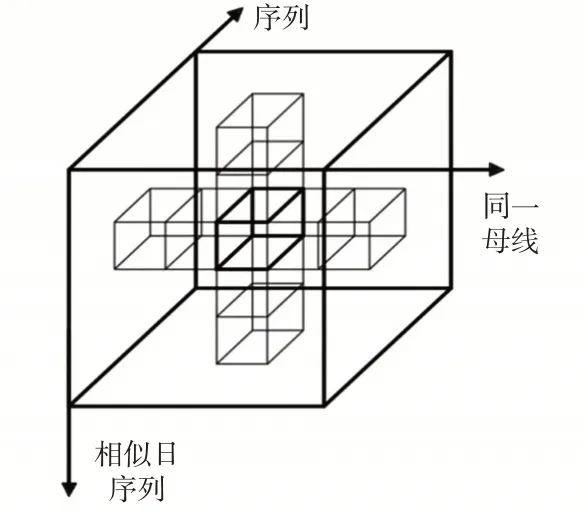
图3 规则化均值修复Fig.3 Regularized mean repair

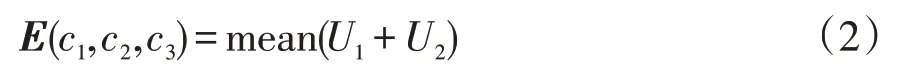
1.3 贝叶斯CP分解张量

贝叶斯CP分解张量基于基本的CP分解完成。1个三阶张量A∈R I1×I2×I3经过CP模型分解后得到了，式中I1×I2×I3为三阶维度；∘表示向量外积；其中a r,b r,c r为分解结果，其维度分别是ar∈R I1,b r∈R I2,c r∈R I3，R即为张量的CP秩[14]。其分解过程的矩阵形式如图4所示。

图4 张量的CP分解Fig.4 CP decomposition of tensor

对于完成初始化的时空张量E可以进行贝叶斯CP分解。时空张量E是实际观测到的具有残缺数据的张量。该假定张量E∈R I1×I2×…×I N，其中I1×I2×…×I N为N阶维度，N为该张量的维度数。E可以分解为低秩张量x与一个噪声张量ε之和，即

根据CP分解张量模型将分解好的低秩张量结合满足高斯分布的噪声张量，即可得到完整的张量分解结果为

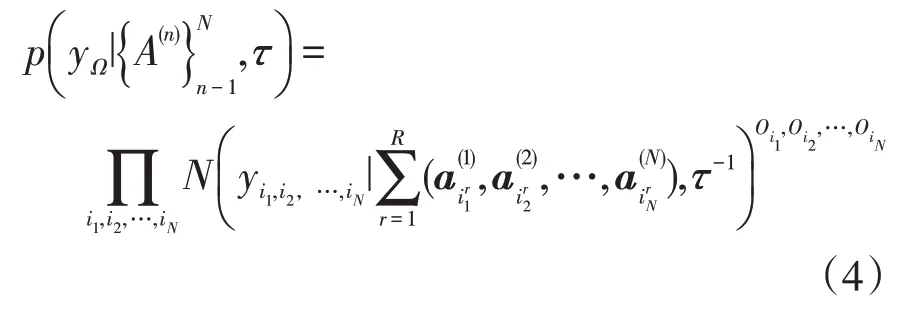
式中：Ω为被观测数据的指标集i1,i2,…,i N；被观测数据为yΩ，O i1,O i2,…,O i N为时空张量的掩模张量，与时空张量大小等，由0，1构成，0表示填充数据的位置；为分解后的CP张量。

为了适应缺值张量秩的可变动，特引入超参数集群。令参数λ的先验分布为伽马分布

式中：λr为参数λ在秩R=r下的伽马分布；为对应的伽马分布形状参数。为了满足全贝叶斯框架，进一步假设噪声ε的精度τ也服从伽马分布，即

式中，b0,b1为伽马分布的形状参数。则观测数据的联合分布为[15]

1.4 缺失张量的修复

在此模型下，通常使用贝叶斯变分推断进行模型求解。在该框架下，通过最小化KL散度获取后验分布来逐次逼近目标s(θ)。其中，s(θ)为推断的近似解。

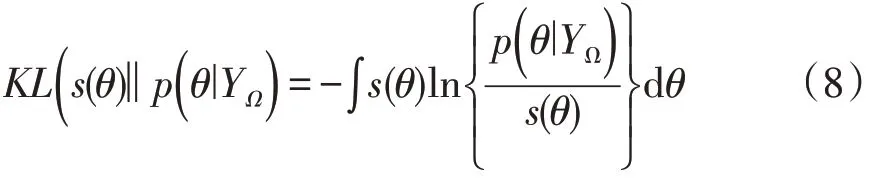
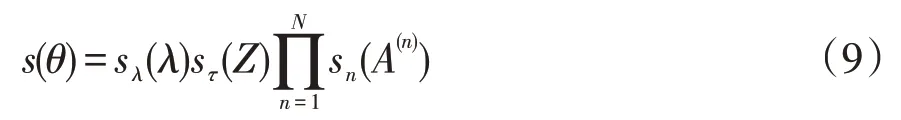
式中：N为分解s n的维度；逼近目标s(θ)等于该目标函数在τ,λ,R3个维度下的sλ(λ),sτ(Z),s n(A(n))积。

通过假定观测函数与实际观测数据的KL散度逐次逼近最小化即可求解超几何参数，由此即可预测缺失数据[16]。

2 算法流程

本文选取某地10 kV线路的电压数据作为数据来源，该线路共计下辖15个台区。数据采集时间为2020-08-17、2020-08-24、2020-08-31，数据采集间隔为15 min，每天共计收集96个点的数据。

此次验证共收集到的3 d相似日数据uT={uT1,uT2,uT3}，同一个时刻下同一母线下共计15个台区电压数据序列u j={u j1,u j2,…,u j15}，在1 d内1个台区共收集96个电压数据，收集到的电压时间序列为

收集到的电压数据从相似日电压时间维度、电压时间序列维度和同一母线电压空间维度构成三维的时空张量。

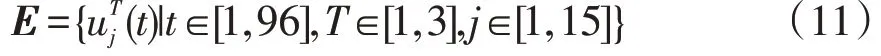
为评价修复数据的准确性，本文收集到的电压数据为完整的原始数据，需要生成和时空张量相等大小的0、1掩膜张量D进行人为数据缺失。0表示对应时空张量数据缺失，1表示对应的时空张量存在，依次来构造缺值的时空张量E0。

掩膜张量共设置10%，20%，30%3组随机缺失数据情况，图5为该条线路下，1号台区于2020-08-17日的数据经掩膜张量处理后的数据缺失情况，虚线部分为缺失数据。为评价数据修复情况特定义数据误差为W，将修复数据E1与原始观测数据E做差并取绝对值，将此差值与原始观测数据E的比值定义为数据误差。

图5 经掩模张量处理后数据缺失情况Fig.5 Missing data after mask tensor processing

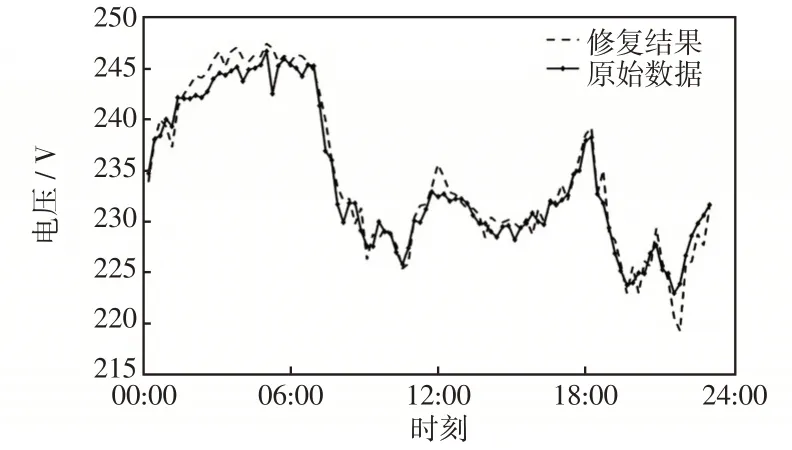
图7 损失20%数据修复情况Fig.7 Repair status with loss of 20%data

经过本文方法处理后，3组缺失数据误差为0.35%、0.41%、0.28%。经过多次试验，随着缺失数据的增加，修复的误差并没有随之增大（如图6~图8），修复数据满足使用要求，大大提高了数据质量。

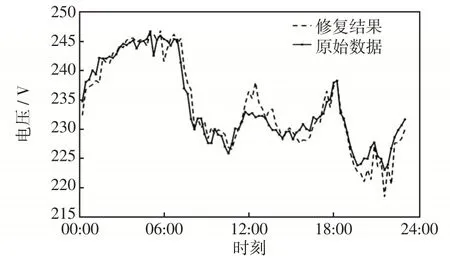
图6 损失10%数据修复情况Fig.6 Repair status with loss of 10%data

图8 损失30%数据修复情况Fig.8 Repair status with loss of 30%data

3 实验与结果分析

为验证本文所提方法的有效性，本文选取了大量实际数据加以验证。本文所用数据源于国网电力有限公司用电采集系统。共选取3条10 kV母线配电网线路，下辖119台配变，共采集2020-08-17、2020-08-24、2020-08-31 3 d数据，数据采集间隔为15 min，每天共计收集96个点的数据。实验平台为一台PC机，其中央处理器为Inter Core i7-8550U，内存为8 GB，算法所用张量计算由Matlab中tensor工具箱完成。

为了充分测试本文所提方法的性能，共使用了某地3条10 kV线路的完整用电数据，人为对其进行缺失破坏。这里使用缺失率参数Q来控制破坏情况。掩模张量中缺值数量由缺失率参数Q确定总量并随机分布与掩模张量。在损失率以5%递增时3条线路修复结果的误差值均小于0.5%。大大提升了原有缺失数据的数据质量。

为验证本方法的有效性，特选取较为常见的移动平均插值法MA（moving average）和主成分分析法PCA（principal component analysis）进行不同数据损失量的修复情况对比。该算例共选取了20条10 kV线路加以计算，并计算出不同缺失数据条件下的误差均值加以比较。观察图9可知，本文所提方法在原始数据损失率不断增加的情况下依旧保持良好的修复准确率，主成分分析法虽然受数据损失率影响较小，但总的修复精度略逊于本文所提方法。

表1 各损失率下的误差结果比较Tab.1 Comparison of error result at different loss rates

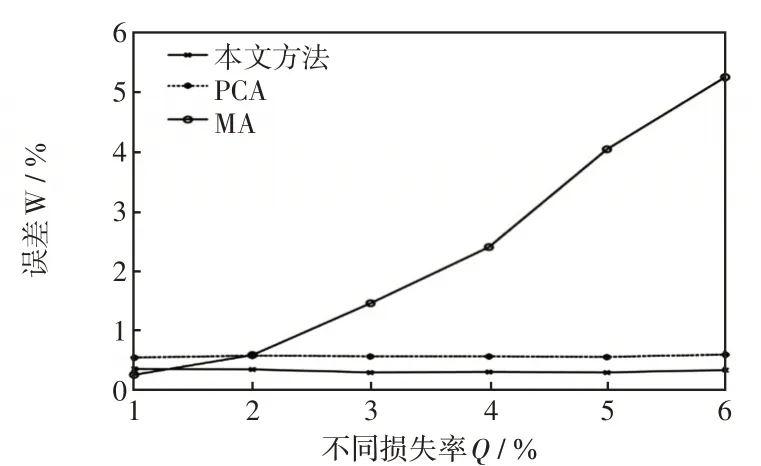
图9 不同方法修复情况Fig.9 Repair results using different methods

4 结论

本文运用张量分解理论下的10 kV配电网电压数据修复方法，有效修复了10 kV配网的缺失数据。通过研究得出如下结论：

（1）首先定义了用电数据的时空张量，丰富数据内在信息联系，利用张量分解理论修复缺值数据。有效发掘了系统中的数据信息。

（2）采用实际配电网数据测试，修复数据的误差在0.5%以下，有效提升了数据质量，对于异常用户监测等其他工程应用有着重要价值。

（3）本文所提方法不需要预先的模型训练，有充分发掘系统中数据的内在联系、计算复杂度较低的优势。

在后续研究中进一步简化模型使之用于实时数据监测，将对数据质量提升有着重要影响，良好的数据将对国网解决线变关系、故障定位、偷电用户监测等问题提供帮助。