基于深度学习的多微电网市场主从博弈运行优化策略

严文君，刘俊勇

（四川大学电气工程学院，成都 610065）

在国家“碳达峰”和“碳中和”双碳目标下，高效、清洁、低碳成为我国乃至世界能源发展的主流方向，以太阳能、风能为代表的新能源将主导未来可再生能源的发展[1]。微电网MG（microgrid）可以协调控制分布式电源，依托互联电力系统实现大范围能源优化配置，是新能源就地消纳和并网远送的主要模式[2-3]。但是传统单一微电网集成各类新能源发电系统的能力有限，将区域内的多个微电网通过相关协议互联形成多微电网系统，有助于区域间不同能源互补，实现高比例新能源消纳，提高互联网络系统的经济效益[4]。

目前，国内外相关领域学者对于多微电网互联系统开展了诸多研究，大多集中在如何实现优化调度[5-7]、能量控制[8-9]等方面。随着电力市场逐步改革开放，微电网作为独立利益主体被允许参与电力市场进行电力交易，在此背景下，研究多微电网参与下的电力市场交易运行机制显得十分必要[10]。多微电网市场中各参与主体间利益不同，且存在错综复杂的多元化交易博弈行为，基于此，文献[11]引入以价格为博弈手段的伯特兰德博弈对不同主体进行博弈行为分析，但是将其运用于多微电网各主体竞争博弈行为时，需要假设分布式电能出力没有上限约束，该约束条件与实际情况不符。古诺博弈以产量作为博弈手段，多被用于分析多发电商地位相等的市场竞价行为[12]，文献[13]收集各发电商竞争对手的报价策略和市场交易信息，通过古诺博弈对信息不断进行迭代，帮助发电商制定最优决策方案。主从博弈[14]是剖析决策者与响应者之间存在先后决策顺序的有效模型，文献[15]根据负荷和电源双重特性，分别建立购售电双方支付函数，建立多虚拟电厂参与电力市场时的双层模型，上层建立多虚拟电厂主从博弈竞价模型，制定直接交易电量策略，下层考虑各虚拟电厂总成本最低得到最优响应功率。传统电力市场博弈模型，各主体都有各自的优化目标函数，需要满足各自利益最优来达到纳什均衡，但互联微电网复杂的系统结构和数学模型以及全局信息获取不足等因素，为纳什均衡求解带来了诸多困难，使模型收敛效率较低且不稳定[16]。

基于数据驱动的深度强化学习方法其具有从高维度、非线性状态空间中提取高阶数据的挖掘能力，为求解复杂博弈模型提供了思路[17]。文献[18]建立了运营商和多虚拟电厂的一主多从博弈模型，通过Kriging元模型模拟虚拟电厂能量内部管理行为，根据动态定价合理安排内部各分布式能源出力；文献[19]中各发电商不需要获取竞争对手的利润函数等信息，在不完全信息博弈过程中，通过Qlearning方法对发电历史数据和自身的经验来进行训练学习，从而确定最优的行动策略；文献[20]针对日前电力市场中发电商投标人的竞价问题，采用多智能体深度确定性策略梯度方法逼近各发电商博弈行为的纳什均衡，为各发电商制定最优竞价策略。

鉴于以上问题，本文提出了基于图卷积神经网络与长短时记忆网络GCN-LSTM（graph convolution neural network-long short-term memory network）时空预测算法的多微电网市场主从博弈均衡策略，并证明了包含多微电网市场各参与主体主从博弈模型存在纳什均衡解。为了更好地实现两阶段主从博弈模型求解，通过图卷积神经网络提取到的市场交易信息构成时间序列数据输入长短时循环网络进行训练，确定市场各主体最优报价策略并下发到微电网实时调控层，根据报价策略进行微电网内报价及设备出力调整，并将调控结果反馈给决策层，通过两阶段相互迭代求解多微电网市场最优报价策略，实现多微电网市场主从博弈均衡运行优化。最后，通过算例分析表明，所提方法有优越的能源整合和盈利能力，通过改变多微电网市场内部多种新能源互补配置，更好地适应市场环境的改变。

1 基于深度强化学习的多微电网市场博弈运行架构

1.1 基于GCN-LSTM的多微电网市场时空预测方法

利用图卷积神经网络将多微电网互联电力市场空间联络拓扑图抽象为图模型G=（V，E），各个微电网被抽象为图模型中的节点集合V，并对其编号①、②、…、⑧。以各微电网内分布式电源出力、负荷需求量以及日前边际电价等信息作为相应图节点的特征向量，将连接各个微电网的联络线抽象为图模型中的边集合E，通过边集合实现市场信息、价格、能源调控配置等数据在各节点间的信息传递。如图1所示，GCN-layer提取多微电网空间特征主要以某节点为中心，对相邻节点信息进行提取，单层GCN只能取一阶相邻节点数据，比如以节点①为中心提取相邻节点②、③、④、⑤的特征数据，由此通过堆叠卷积神经网络卷积层数获取全局整体节点特征数据[21]。

通过建立GCN图模型对多微电网互联电力市场进行描述，体现出各微电网分布式电源出力、负荷需求量以及日前边际电价等信息，受到地理环境、社会生活生产规律而体现出一定的周期性、规律性和关联性关系，以此通过对多微电网市场历史状态进行分析计算实现对未来电力市场状态预测。本文通过图卷积神经网络GCN（graph convolu⁃tion neural network）和长短时记忆网络LSTM（long short-term memory network）相结合构建多微电网市场时空预测算法。LSTM主要被用于长序列数据训练，图1中LSTMCell为长短时记忆网络的1个神经元，其包含4个神经网络层，并通过遗忘门、记忆门和输出门实现神经元中信息的删减和增加。LSTM运算机理本文不再赘述，见文献[22]。

图1 GCN-LSTM时空预测算法结构Fig.1 Structure of GCN-LSTM spatial-temporal prediction algorithm

1.2 多互联微电网市场两阶段博弈运行机制

多微电网主要包括的各主体：多微电网市场运营商、微电网分布式发电设备、负荷聚合商和储能设备，多微电网市场运营商负责多微电网各主体交易与运营管理；分布式电源作为源侧，通过分布式风电、微型燃气轮机等分布式发电设备为微电网内外提供稳定可靠的电力；负荷聚合商包括固定负荷、可平移负荷及可削减负荷等，通过有偿调节用能行为参与互动响应，充分调动可控负荷的积极性。储能设备通过充放电来补偿分布式发电出力波动性和不可控性，增强微电网接纳分布式能源发电能力和提高能源利用效率。

如图2多微电网市场两阶段运行架构所示，在多微电网电力市场中，各微电网作为统一主体参与配网侧电力市场进行交易，微电网运营商聚合自身服务范围内的灵活性资源，综合分析外部不完全市场交易信息以及自身源荷运行数据，确定最优运行策略，促进多微电网市场能量供需平衡。多微电网互联系统分布式调度机制主要包括两个阶段：市场报价决策阶段和微电网实时调控阶段。各微电网运营商在前一天上报未来24 h的发电量和报价情况，配电网交易中心对报价信息和系统运行参数进行综合分析，以各微电网整体净效益最大化为目标，确定各微电网中标电量和中标价格。各微电网运营商据此优化下一阶段报价策略，多微电网市场报价阶段和出清阶段存在顺序衔接关系，经过两阶段循环交互，实现多微电网市场运行优化。

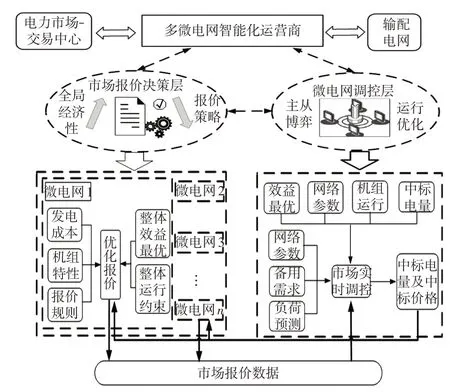
图2 多微电网市场两阶段运行架构Fig.2 Two-stage operation framework for multimicrogrid market

2 多微电网市场两阶段主从博弈模型

2.1 多微电网市场报价决策模型

本文微电网内电源出力主要以风电出力为基准场景，阶段一为多微电网市场报价阶段，各微电网根据自身机组运行特性和市场交易规则以自身净效益最大化为优化目标进行报价，其优化目标函数表达式为

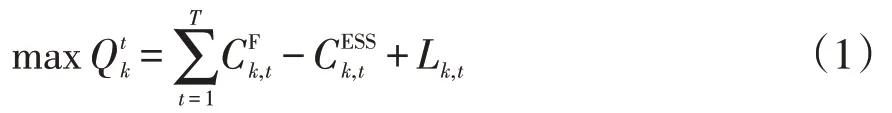
式中：为第k个微电网在t时段的净效益函数；T为时间段，取T=24；为t时段第k个微电网的电能交易效益；L k,t为t时段第k个微电网用户的效用函数；为t时段第k个微电网储能系统的充放电成本，各表达式具体形式为

式中：、分别为t时段多微电网市场的内部预测购电价和售电价；、分别为t时段第k个微电网的购电量和售电量。

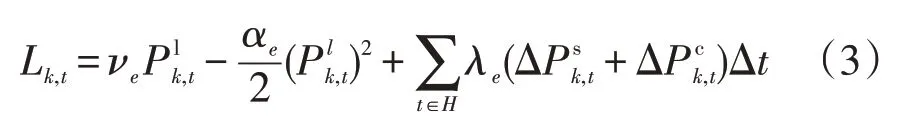
式中：νe、αe为用户消费电能所获得的满意度系数；H为t时段微电网内负荷响应时间的集合；λe为削峰填谷单价；为t时段第k个微电网的预测负荷需求量；Δt为响应的时间长度；为在时刻t上报的可平移电负荷和可削减电负荷。

阶段一的约束条件主要包括功率平衡约束、微电网与配电网之间功率交互功率约束、储能设备充放电功率约束等，具体约束表达式如下：

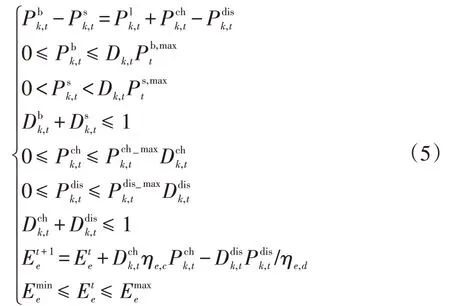
式中：与分别为微电网在t时段的购、售电功率的最大值；D k,t为状态系数；为购电状态系数，购电时取1，未购电时取0；为售电系数，售电时取1，未售电时取0；分别为储能装置k在t时刻最大充放电功率；为充放电后、充放电前的储能量；为储能装置充电状态系数，充电时取1，未充电时取0；表示储能装置放电状态系数，放电时取1，未放电时取0；ηe,d表示储能装置放电量系数；ηe,c表示储能装置放电量系数；分别为储能系统的储能量上下限。

2.2 多微电网市场实时调控主从博弈模型

在微电网实时调控阶段，微电网运营商在考虑上层决策方案的前提下，结合自身内部多余电量和负荷需求，以降低设备调控运行成本为目标，优化微电网设备出力情况，目标函数为

式中：A为实时调控时间尺度；M为分布式电源设备数量；ΔCG,up为分布式发电设备实时调控上调成本；ΔCG,down为分布式发电设备实时调控下调成本；ΔCESS为储能设备实时调控成本；ΔCM为实时交易成本；分别为分布式发电设备i在t时刻的上调功率、上调单位功率成本；分别为分布式发电设备i在t时刻的下调功率和下调单位功率成本分别为储能设备t时刻充放电调控功率；分别为微电网向外电网购电和售电调整量；λM为调整电价。

为保证多微电网市场在两阶段主从博弈模型下安全运行，需要对各微电网进行安全校核。为此，结合微电网网络约束条件，建立多微电网市场优化运行约束。

考虑微电网内部各节点之间的线路功率传输约束，其支路潮流[23]形式为

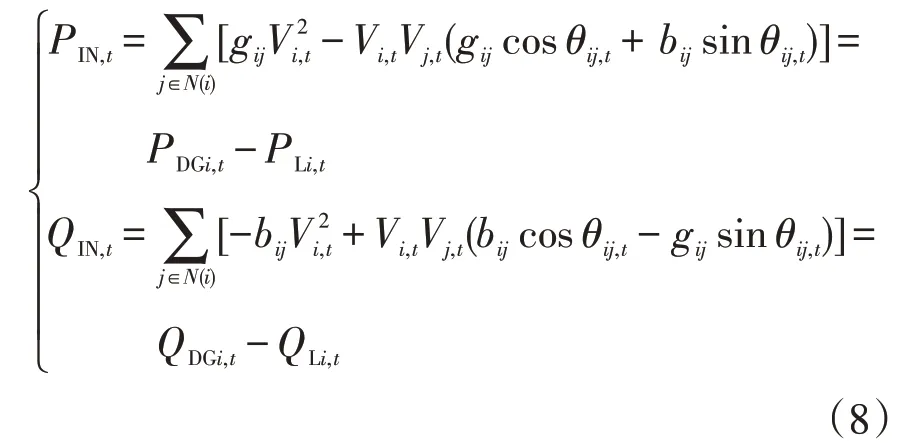
式中：PIN,t、QIN,t分别为t时刻节点i的注入有功、无功功率；θij,t为t时刻节点ij间的相角差；N(i)为所有与节点i相连的节点集合；V j,t为t时刻节点j的电压幅值；Vi,t为t时刻节点i的电压幅值；gij、b ij分别为支路ij的电导和电纳；PDGi,t、PLi,t、QDGi,t与QLi,t为t时刻分布式电源和负荷的有功、无功功率。

网络安全运行的功率传输需满足的约束为

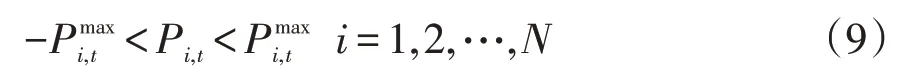
式中：P i,t为在t时刻支路i功率；为支路i最大传输功率。若通过支路i的潮流满足式（9）的约束，则完成网络安全验证，并执行经济最优策略计划；若不满足，则需要进行阻塞管理措施。考虑以上约束情况，通过计算支路i、的潮流变化灵敏度a P,i和aQ,i对功率进行进一步调整，调控功率表达式为

式中：Ng为微电网节点个数；ΔP i、ΔQi为节点i注入有功、无功调控功率。灵敏度的求解过程见文献[24]。

3 模型求解

3.1 基于GCN-LSTM的报价策略流程

本文基于GCN-LSTM深度强化学习方法的多微电网阶段一报价策略确定流程如图3所示。

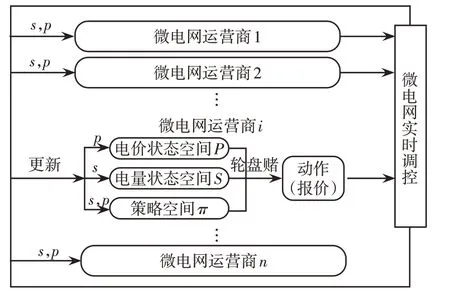
图3 多微电网市场阶段一报价策略流程Fig.3 Flow chart of quotation strategy at Stage 1 in multi-microgrid market

（1）生成状态空间。将微电网发电设备出力和电价区间划分为x段，每一段生成对应的电量状态空间P及电价价状态空间S。

（2）生成策略π及选择报价曲线。报价策略初值设置为各报价曲线的选择概率相同，随着交互迭代进行，以轮盘赌的方式在报价状态空间中随机选取一条报价曲线并执行。

（3）确定中标电量p与电价s。根据所有微电网的报价信息，统筹分析各微电网效益，并将该中标结果反馈给各微电网进行实时调控。

（4）策略π更新评价。平均策略和当前策略下得到的期望值评判策略优劣。

3.2 纳什均衡证明

本文纳什均衡存在证明过程如下。

阶段二微电网市场调控运行优化问题可以描述为一个领导者（交易中心）与多个跟随者（微电网运营商）间的一主多从的Stackelberg博弈问题，微电网运营商通过响应交易中心的价格信号确定其内部最优出力策略和负荷需求策略。

1）Stackelberg均衡存在条件一

由第2.1、2.2小节所建立的模型可知，微电网中各参与主体的博弈策略集合均需要满足约束式，即满足Stackelberg均衡存在条件一：每个参与者的策略集合都是非空且紧凸。

2）Stackelberg均衡存在条件二

在领导者（交易中心）的报价决策确定的条件下，对目标函数式（6）分别求关于的一阶偏导数方程，令其方程等于0，可以得到理论上的最优值。即当领导者的策略给定以后，所有跟随者均存在唯一最优解，满足Stackelberg均衡存在条件二。

3）Stackelberg均衡存在条件三

阶段一的各微电网市场效益函数（1）是在策略状态空间内的分段函数，且在每一个子定义域空间内是凸函数。因此，效益函数存在局部最优购售电价求得局部最优值，通过比较收益值大小，即可得到全局最优效益，满足Stackelberg均衡存在且唯一的条件之三。

综上可知，本文提出的多主体主从博弈模型，存在唯一的Stakelberg均衡。

3.3 多微电网市场两阶段模型求解

鉴于多微电网市场两阶段中的决策问题均属于大规模非线性优化问题，且优化目标函数是二次函数，采用深度强化学习可以实现结果准确的前提下的算法简化，因此，本文通过二次规划结合深度学习训练方法求解，搜索Stackelberg最优均衡策略，具体求解步骤如下。

阶段一市场报价决策阶段：

步骤1调取多微电网市场数据信息通过GCN-LSTM进行数据挖掘优化新能源、负荷及储能设备预测信息（多微电网内部购售价、配电网市场购售价、新能源出力、负荷需求、储能计划等），输入训练模型参数；

步骤2初始化滚动优化训练模型，确定报价策略，并更新策略因子；

步骤3判断是否满足停止准则，若满足，则得到第一阶段市场报价策略最优解；若不满足，则再一次进行滚动训练，返回步骤2，直至收敛。

阶段二微电网实时调控阶段：

步骤1微电网运营商收集微电网上报的下一时段新能源出力预测值、阶段1滚动优化后确定下一时段微电网市场预测信息，输入训练模型参数；

步骤2初始化微电网运营商相关参数；

步骤3微电网运营商接收交易中心的价格信号，根据其定价进行二次规划；

步骤4微电网运营商接收反馈的功率信号，供用关系计算其收益，进行训练、动作、评价，实现滚动优化更新；

步骤5求解相邻两次各博弈方当前策略，判断是否达到最优策略均衡；

步骤6若满足最优策略组合则输出结果，若不满足，则返回步骤3，直至该策略组合收敛到均衡点。

4 算例分析

4.1 算例设计及基础数据

本文将IEEE 33节点系统分解为3个微电网区域，其中节点1、节点6、节点22为连接节点，其具体划分范围如图4所示。两区域微电网间联络线传输极限为10 MW。各微电网设备容量配置及节点位置如表1所示，储能设备相关参数最大和最小荷电状态SOCmin和SOCmax如表2所示。多微电网市场设定各微电网的初始报价等于配电网市场节点边际电价，设为0.078 3USD/（kW·h），竞价功率范围设为0~3 MW，其他设备参数设置详见文献[25]。

图4 多微电网市场IEEE 33节点系统拓扑Fig.4 Topology of IEEE 33-node system in multi-microgrid market

表1 分布式设备容量配置及节点位置Tab.1 Capacity configuration of distributed equipment and location of nodes

表2 储能设备相关参数Tab.2 Related parameters of energy storage equipment

设置学习率为0.001，设置含两层GCN网络（22，72×192）、（22，76×96），其中22为节点数，76为批训练大小，22×96为LSTM网络隐状态维度，全连接层输出维度设置为1，选择adam作为优化训练器。软件采用Python编程语言，硬件采用CPU i7-10700，显卡为RTX 2060，在Windows10环境实现模拟测试。

4.2 算例结果分析

通过GCN-LSTM算法对各个微电网新能源出力、负荷等信息进行预测，掌握市场供需情况，如图5所示。选取10：00—11：00段进行竞价分析，各微电网运营商在GCN-LSTM方法预测结果基础上，更准确地掌握了市场动态，仅在5次竞价后市场达到均衡，且各微电网运营商报价均高于市场的节点边际电价，微电网运营商1报价最高为0.082 9$/（kW·h）；微电网运营商3报价次之为0.080$/（kW·h）；微电网运营商2报价最低，为0.078 5$/（kW·h），如图6所示。以上价格为此时段的市场出清电价。

图5 各微电网典型日24 h源荷预测情况Fig.5 Source and load prediction of each microgrid in 24 h on typical day

图6 多微电网市场竞价曲线Fig.6 Bidding curve in multi-microgrid market

基于阶段一决策优化结果，不平衡的微电网参与到多区域微电网市场主从博弈优化运行中，如图7所示，从各微电网整体趋势上看，各个微电网的分布式电源出力与负荷情况各有不同，各微电网与外部电网进行电量交互情况也存在差异。图7中与配电网市场交互电量正值为微电网向外卖电来获取经济收益，交互负值为从外界电网购电来满足自身负荷需求；储能正值为给自身充电，负值为向外放电。从图7中可以看出MG1大部分时间都在向外界输送电量，例如，在0时段至7时间段内，MG1多向外输送电量，为MG2、MG3储能设备充电，并满足当地负荷需求，其原因主要是MG1内风电和光伏装机容量较大，风电和光伏机组出力在较好满足本区域微电网的负荷需求基础上，将过剩的电量向外界输送获取经济收益；MG2、MG3则更多的需要从外界购电来满足各自区域内的负荷需求。在大部分的时间内，各个微电网市场之间都是在互补支撑运行，体现本文所提方法在对多微电网市场协调博弈竞争方面的优势。

图7 各微电网主从博弈实时调控优化情况Fig.7 Real-time scheduling and optimization of masterslave game of each microgrid

在阶段一确定了市场各主体最优决策策略，各微电网通过本文所提主从博弈模型进行实时调控，其实时调控效果如图8所示，除了在时段8本文所提实时调控出力与实际出力出现较大偏差，其余时段均实现了较高准确度实时调控，满足了多微电网市场功率调控能够跟随微电网市场实际调控需求。

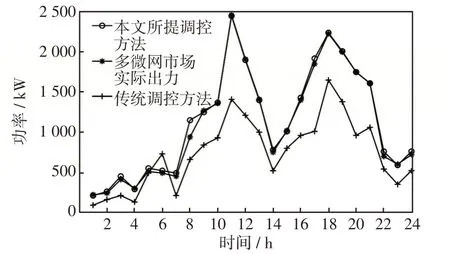
图8 多微电网市场整体功率实时调控效果对比Fig.8 Comparison of real-time scheduling effect on overall power in multi-microgrid market

为了验证本文所提方法带来的收益增加，对两种方案下的各微电网经济收益做出了对比，方案1为多微电网市场主从博弈机制；方案2为各微电网仅以合作模式参与市场，如表3所示。各微电网运行收益方面，方案1收益均高于方案2，方案1能更准确的把握市场运行状态，更精确制定各微电网内调控策略，降低各分布式设备调控成本。

表3 不同方案下的效益Tab.3 Benefits in different schemes

文中所提方法与其他预测算法的价格预测结果对比情况如表4所示，其中RMSE表示预测值与实际值均方根误差、MAE表示预测值与实际平均绝对误差、R2表示预测值与实际值的相似程度。由表4可以看出文中所提方法RMSE、MAE的计算值较其他两种算法均有下降，R2有明显提升，验证了本文所提方法的有效性和准确性。

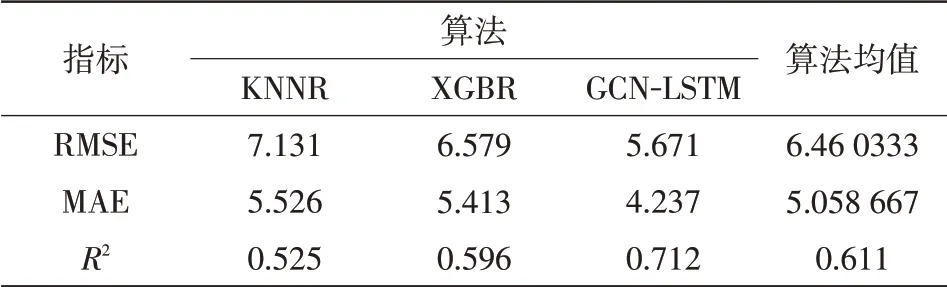
表4 文中所提预测算法与其他算法的价格预测结果Tab.4 Price prediction results of the proposed prediction algorithm and other algorithms

5 结语

本文提出了提出基于GCN-LSTM时空预测算法的多微电网市场主从博弈均衡运行优化方法，该方法在一定程度上解决了传统博弈论方法存在高维度、非线性的问题，也有助于各微电网制定最优的报价决策策略。将多微电网市场中各主体间的相互作用构建两阶段滚动优化模型，通过两阶段模型相互迭代求解确定了多微电网市场最优报价策略，实现多微电网市场博弈均衡运行优化。最后通过算例分析表明，本文所提方法能有效的提高了新能源消纳率，增加微电网市场各竞价微电网经济效益。