高压直流输电线路故障初始阶段解析方法研究

曹 虹，周泽昕，吕鹏飞，谢仲润，李博通，徐 凯

（1.中国电力科学研究院有限公司电网安全与节能国家重点实验室，北京 100192；2.国家电网有限公司，北京 100032；3.天津大学智能电网教育部重点实验室，天津 300072）

随着我国直流系统规模的逐年扩大，其故障几率也在逐渐增多，相关统计数据表明，直流系统故障主要为直流线路故障[1-3]。长距离直流输电线路的故障暂态发展过程会受多种因素影响，包括：远距离输电情况下线路的分布电容电流现象明显，故障电流会受到线路电容电流放电过程的影响；由于长线路的参数频变特性，故障电气量的行波传输过程会出现色散现象，行波波头捕捉困难；直流线路故障过程及电压电流暂态特性受两侧换流器的快速故障控制的直接影响；故障暂态过程中的谐波特性会与滤波器、平波电抗器等设备的参数配置密切相关[4-5]。受以上因素影响，高压直流输电线路的故障暂态特征复杂，变化机理量化困难。研究初始阶段的电气量故障暂态特性及变化机理，对进一步改进和完善直流线路的保护原理和保护方案、保证系统的安全可靠运行等方面具有重要的理论意义和实用价值[6]。

直流线路故障发生后的初始阶段，主要指的是由故障首行波所引起的直流系统暂态过程阶段，不考虑其后第二次折反射行为和控制系统作用。对于直流线路故障初始阶段的时域暂态特征，已有专家学者多对故障后暂态行波的时域解析方法进行探究。文献[7]通过建立复频域下直流线路频变参数惯性等值模型和换流器PI控制等值模型，提出了直流线路故障的时域解析方法，但首行波的解析结果与实际仿真结果有一定差异，不利于后续直流线路保护定值整定的研究。文献[8]提出了一种降序自适应分段匹配算法，用于在相频域内对离散频率响应进行有理频域模型识别，并且基于拉式反变换和精细积分法实现时域电压、电流行波的求解，实现直流线路任意故障条件下时对故障行波准确而快速地计算。文献[9]以无畸变线路模型为基本条件，通过选取合适的相模变换矩阵，根据同塔双回直流线路发生单极线接地故障的边界条件联立方程，推导出了同塔双回直流线路故障电压电流行波的求解公式。

对于直流线路故障初始阶段的频域暂态特征，已有专家学者通过研究直流线路边界元件的频域特性，进一步推导分析区内外故障下频域特征差异。文献[10]分析了直流输电线路的频率特性和边界特性对区内、外故障行波暂态量差异的影响，确定了能可靠区分故障位置的有效频带，并分析了过渡电阻等因素对该有效频带的影响。文献[11]针对在长距离直流线路的频率相关特性，指出故障电气量中的高频分量包含位置主频和边界主频两部分，故障高频暂态量是位置主频和边界主频共同作用的结果。文献[12]分析了高压直流输电长线路的高频信号衰减作用，以600 Hz电压电流作为特征量，提出区内故障时，600 Hz特征分量上升速度快于区外故障。文献[13]分析了故障电流由换流器侧到线路、线路到换流器侧和在线路上的传播特性，进而推导了区内和区外故障下的电流表达，分析了电流故障特征在特定频段下的差异性。文献[14]分析了由平波电抗器、直流滤波器和PLC滤波器等元件构成的特高压直流输电线路边界的频率特性，讨论了非故障性雷击、金属性接地、高阻接地及换相失败情况下不同故障暂态信号的频谱特性。

综上所述，目前已有研究成果主要对故障初始阶段的暂态信号的时频域定性特征进行了一定的研究，已有结论一般作为具体保护判据的区内外故障特征差异的定性分析，并不系统和具体。针对线路滤波设备（如平波电抗器、直流滤波器等）、线路参数的耦合及频变特性对故障特性的影响的研究也并未给出具体的定量分析结论。

针对上述问题，本文对高压直流输电线路故障初始阶段的暂态特性和故障机理进行深入研究。首先，建立了高压直流系统各元件的暂态等效模型；然后，进一步提出了故障电气量中首行波暂态量的解析计算方法；在仿真验证所提故障解析方法的基础上，对等效模型的适用性和影响故障解析的因素进行了分析；最后，根据所提解析方法，对故障初始阶段暂态电流的时域特性进行了系统性分析。

1 用于故障暂态分析的高压直流输电系统等效模型

高压直流输电系统主要由换流器、平波电抗器、直流滤波器及直流输电线路组成，如图1所示。为分析直流线路故障初始阶段的暂态特征，需要建立直流系统故障暂态分析简化等效电路，下面分别对直流系统各元件的等值模型进行研究。

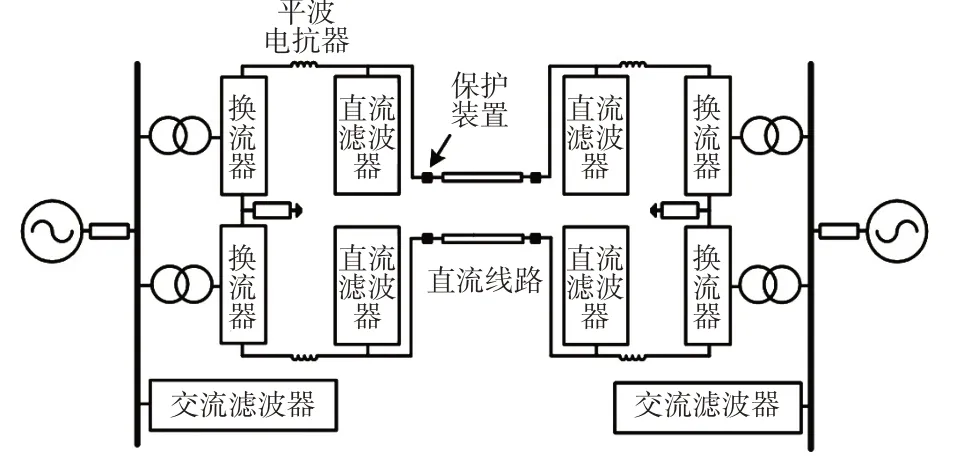
图1 高压直流输电系统结构拓扑Fig.1 Topology of HVDC transmission system

1.1 LCC换流器等效模型

1.1.1 LCC换流器控制系统对故障的响应

当线路上产生的入射波经线路传递到达线路边界瞬间，其在保护处的首行波反映的是此时系统一次结构对故障的响应，该瞬间的系统拓扑决定了入射波的折射和反射系数，从而形成了保护处的故障首行波。然而故障首行波由于线路的色散作用，以及线路边界处电感、电容等元件的折反射作用，其行波不再是瞬间变化的阶梯波，其行波波头的上升及衰减都需要一定的时间。随着时域的发展，系统暂态电气量会因极控和阀控的作用而发生改变，极控在故障后由于输入测量电气量的变化实时改变换流器触发角控制定值，阀控在数毫秒内响应改变换流器运行状态，保护处的电压、电流都会受到换流器控制作用的影响而发生改变。然而，在故障初始阶段的暂态过程中，由于定电流控制中的惯性环节及PI控制器的延缓作用，可以认为在初始阶段控制系统输出的触发角定值指令变化较小，换流器输出电气量未发生明显变化[15]。因此，在因故障首行波到达引起测量电气量变化的初始阶段内，可以忽略换流器控制作用的影响。

1.1.2 LCC换流器等值阻抗

对于12脉动换流器，正常运行状态下换流器的换相角一般小于30°，12脉动换流器工作于“4—5”工况，即4个阀和5个阀轮流交替同时导通的工况。因此，当仅分析故障初始波过程时，故障首行波到达换流站瞬间换流器的通路如图2所示，在非换相期，上下2个6脉动桥中只有4个阀同时导通，通路如图2中点虚线所示；当有1个桥进行换相时，有5个阀同时导通，通路如图2中长虚线所示。图2中：ZS为交流系统内阻；Zdcfl为交流滤波器的等值阻抗；ZT为换流变压器的阻抗。

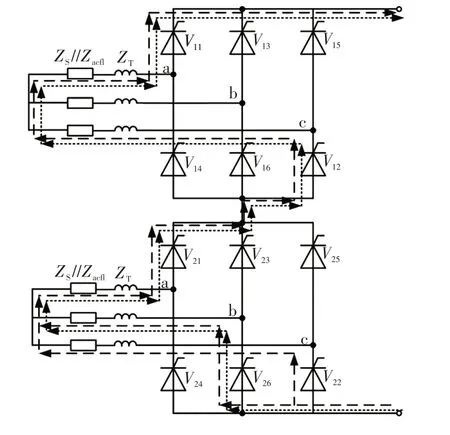
图2 LCC换流器等值电路Fig.2 Equivalent circuit of LCC converter

此时换流器的等值阻抗可根据图2中等值电路列出，即

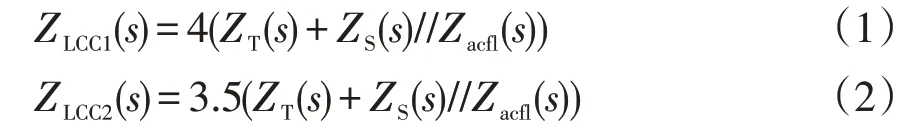
式中：ZLCC1为非换相期间LCC换流器的等值阻抗；ZLCC2为换相期间LCC换流器的等值阻抗。

由于换流器在换相期间和非换相期间暂态阻抗呈脉动变化，考虑控制系统未响应，换流站等值阻抗可取值为脉动周期（包括换相期和非换相期）的平均值[16]，即

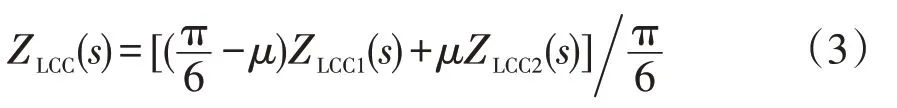
式中：ZLCC为LCC换流器的平均等值阻抗；μ为换相角；π/6为12脉动换流器的1个脉动周期。

1.2 滤波设备的等值模型

在常规高压直流输电系统中，直流输电线路两端通过直流滤波器和平波电抗器连接于直流母线，上述滤波元件构成了直流线路的边界。本文选用的模型中，直流滤波器结构采用双调谐滤波器，主要滤除12次和24次谐波。直流线路边界结构如图3所示。

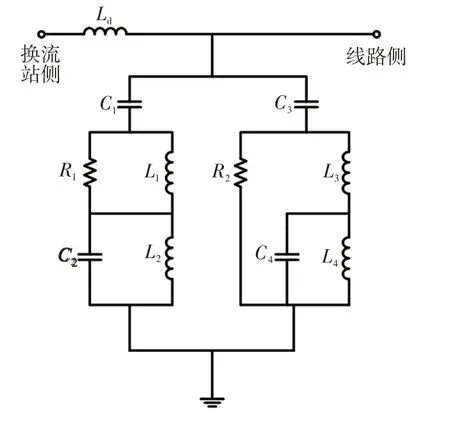
图3 直流线路边界结构Fig.3 Boundary structure of DC line

图3 中：Ld为平波电抗器的电感；R i、Li、Ci（i=1，2，…）分别为直流滤波器的电阻、电感和电容元件参数。根据图3所示的直流线路边界结构，平波电抗器的等值阻抗ZLd如式（4）所示。对于直流滤波器，由于并联电阻R1和R2的阻值一般比较大，为简化计算，忽略并联大电阻后直流滤波器的等值阻抗Zdcfl为

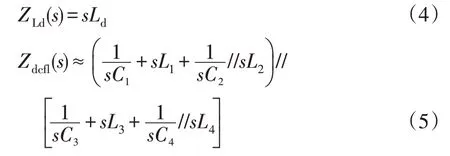
1.3 直流输电线路的简化频变参数模型

为了精确分析故障初始阶段的波过程，需要考虑行波传输过程中线路频变参数特性的影响。根据文献[7]，在复频域中，线路传递函数e-γ(s)l可以用2个复频域函数乘积进行近似简化为

式中：γ(s)为线路的传播常数；l为线路长度；惯性环节(1-kal)/(1+sτal)用于描述行波传播过程中的衰减和畸变；ka为衰减系数；τa为色散时间常数；e-sl/ν用于描述行波沿线路传播带来的延时；v为行波波速。

2 故障首行波的时域解析计算

对于发生在tf时刻的故障，设故障距离为x，行波波速为v，故障首行波到达保护的时刻为tf+x/v。而行波经折反射后，第二个行波到达保护的时刻为tf+3x/v（故障点反射波），或tf+(2l-x)/v（线路另一端反射波，l为线路长度）。因此，故障首行波分析的有效时间为[tf+x/v,min{tf+3x/v,tf+(2l-x)/v}]，此时可以认为处于故障初始阶段，该阶段内系统某一点电气量由故障前稳态分量和首行波暂态分量构成[17-18]。

根据图1所示高压直流输电系统，本节以直流线路上整流侧保护处测量值为例，对直流线路发生单极接地故障时故障首行波的详细解析计算过程进行阐述。直流线路发生单极故障的示意图如图4所示，直流线路LineMN的整流侧正负极保护装置用Mp和Mn表示；ZLCCM为整流站M的等值阻抗，ZLCCN为逆变站N的等值阻抗；ZLd为平波电抗器电感；Zdcfl为直流滤波器等值阻抗。

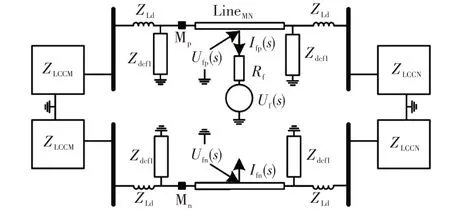
图4 传输线单极接地故障示意Fig.4 Schematic of transmission line under single-pole-toground fault

2.1 直流输电线路的简化频变参数模型

由于故障激励源的作用，故障点正极和负极电压分别为Ufp(s)和Ufn(s)，正极和负极电流分别为Ifp(s)和Ifn(s)，故障激励源电压为Uf(s)，故障处过渡电阻为Rf。上述电压和电流形成了向故障点两侧传递的入射行波。根据图4所示故障点处电压、电流关系，可以列出直流系统单极接地故障的边界条件为

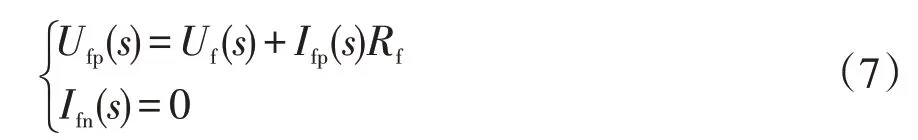
为方便统一分析故障行波在双极直流线路上的产生、传播和折反射，本节利用解耦矩阵，将正、负极电气量变换为1模、0模电气量，在模域中对故障行波进行解析。解耦矩阵为

式中：a为系统某一点电气量（电压或电流）；下标p和n分别表示正极和负极，下标1和0分别为1模和0模。

故障时1模和0模网络如图5所示，图中Uf1(s)和Uf0(s)分别为故障点1模和0模的复频域电压；If1(s)和If0(s)分别为故障点1模和0模的复频域电流；ZF1(s)和ZF0(s)则分别为由故障点看入的1模和0模故障网络的等效阻抗。

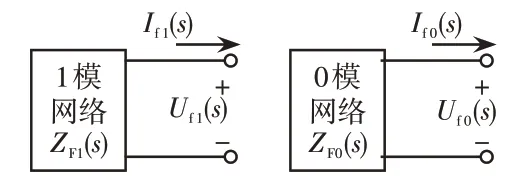
图5 模域网络示意Fig.5 Schematic of mode-domain network

根据图5，故障点的模域电压和电流关系式为

联立式（7）~（9），可得故障点模域电气量为

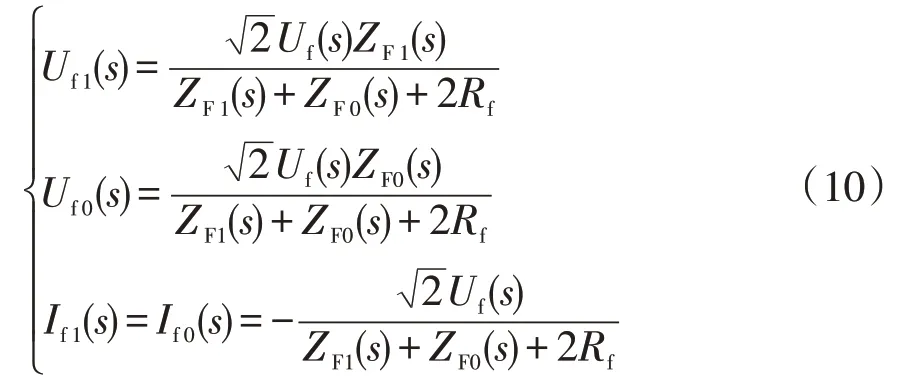
由式（10）可知，单极接地故障时1模网络和0模网络相当于在故障点与故障附加电压源 2U f(s)和电阻2Rf相串联，模域故障网络如图6所示。Zc1和Zc0分别为直流线路的1模波阻抗和0模波阻抗。

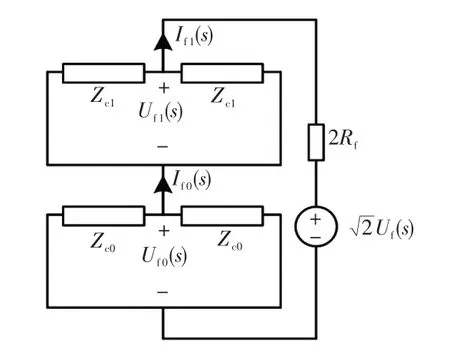
图6 单极接地故障时故障点模域网络Fig.6 Mode-domain network at fault point under singlepole-to-ground fault

由图6可知，故障点处看入的1模和0模故障网络等效阻抗ZF1(s)和ZF0(s)为

另外，对于直流线路首端和末端出口处故障，求解直流线路上产生的故障入射波时，其故障点的模域网络阻抗不再为式（11），而需根据直流线路边界的结构列出，如图7所示。直流线路首端、末端故障时故障点1模和0模故障网络等效阻抗分别为

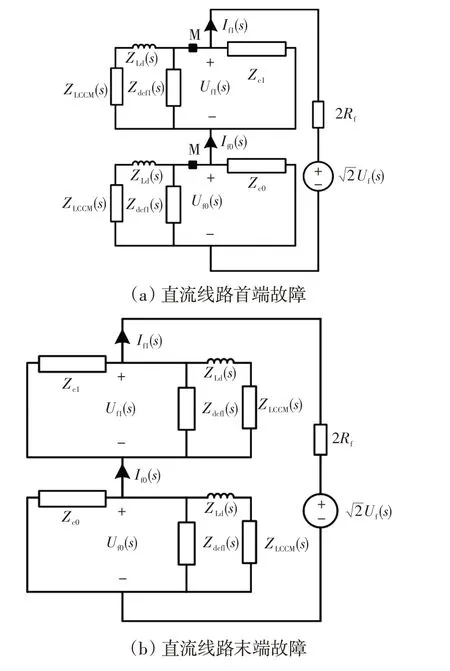
图7 线路出口处发生单极接地故障时的故障点模域网络Fig.7 Mode-domain network at fault point under singlepole-to-ground faults occurring at DC line ends

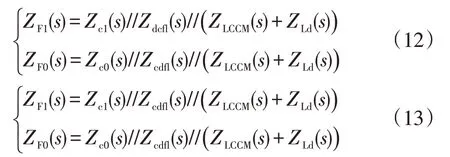
对于直流线路故障，将式（11）~（13）代入式（10）即可计算得到故障点电气量，即为直流线路上的入射行波。对于保护M处的电气量，除了线路首端故障情况下可以直接通过式（10）计算得出外，其他位置发生故障时故障点产生的入射波向保护M处传递，需要对入射波在线路上的传递过程和在保护M处的折反射进行进一步计算。

2.2 直流输电线路的行波传递和折反射过程

根据上述计算，可以得到电压入射行波U f1(s)和U f0(s)，这些入射电压行波向保护M处传递，行波的传递过程如图8所示。图8中，BM1(s)、BM0(s)表示经历直流线路传播过程后到达保护M处的电压入射行波，UM1(s)、UM0(s)、IM1(s)、IM0(s)分别表示保护M处的暂态电压和电流。

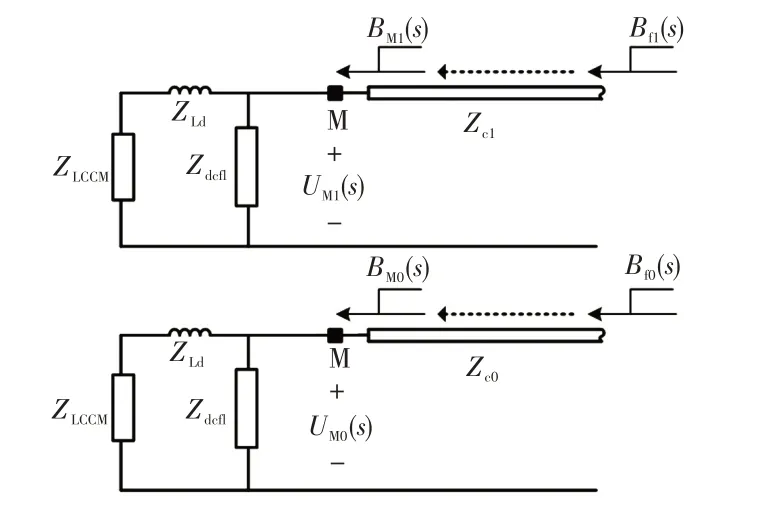
图8 行波传播示意Fig.8 Schematic of propagation of traveling wave

该过程可以描述为

式中：线路传递函数e-γ1(s)x、e-γ0(s)x选用1.3节中给出的简化模型，下标1代表1模参数，下标0代表0模参数；x为故障点到保护M处的距离。

通过式（14）可以求得首个到达保护M处的电压入射行波BM1(s)和BM0(s)，而后再通过保护M处的电路结构解析反向电压行波的折反射过程，从而计算出保护M处的电压首行波理论值。由于M点线路侧为分布参数的长线波阻抗，M点换流器侧为集中元件的集中阻抗，两侧波阻抗不同，因此入射波会在保护M处发生折反射，根据图8，1模和0模行波传播到保护M处的电压反射系数β1和β0为

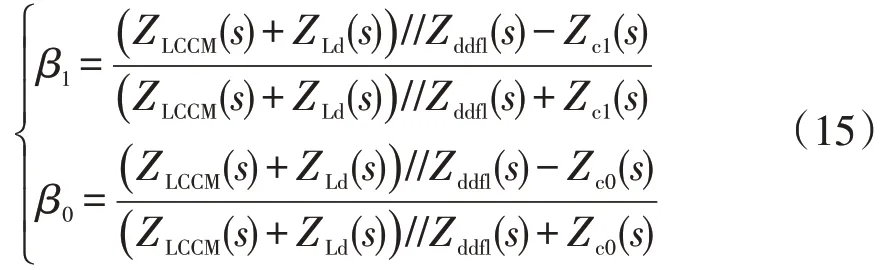
根据行波折反射理论，保护M处的电压首行波为入射波与反射波的叠加，因此保护M处故障电压首行波表达式为

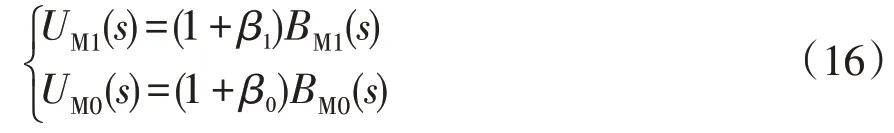
另外，根据电网络结构，保护M处的电流首行波表达式为

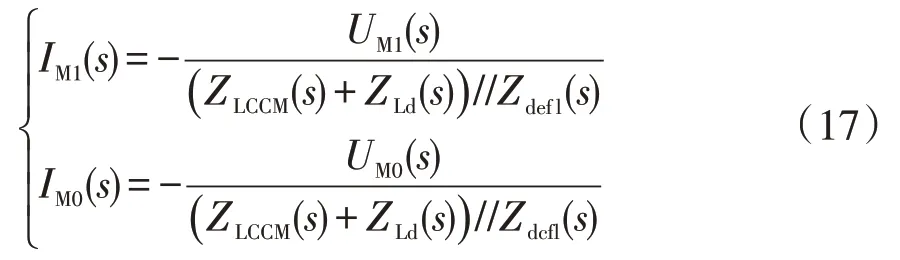
图4中故障点处附加激励源Uf(s)可视为阶跃信号，与该点故障前电压大小相等且方向相反，故Uf(s)的复频域为

式中，Udc为正极线路正常运行电压。

联立式（10）、（15）~（18），再将一模、零模电气量变换为正、负极电气量，则保护M处正极电压UMp(s)、负极电压UMn(s)、正极电流IMp(s)、负极电流IMn(s)分别如式（19）和式（20）所示。

式中，ZM(s)=[ZLCCM(s)+ZLd(s)]//Zdcfl(s)为线路端口M侧的等效阻抗。

通过以上分析，可得到不同单极接地故障位置下故障初始阶段的电压、电流首行波复频域表达式。对于双极短路故障，分析求解过程类似，不再赘述。

对于以上不同故障类型、不同故障位置的正、负极电压、电流首行波复频域表达式，可运用拉氏反变换求取故障初始阶段保护M处的正、负极电流首行波itwMp(t)、itwMn(t)的时域解析表达式。

2.3 时域解析值求解

由于拉氏反变换求解过程比较复杂，复频域方程阶数较高，本节以典型高压直流输电系统参数为例，将具体参数代入电压、电流首行波复频域表达式，并考虑叠加故障前正常运行电压、电流，求解故障初期正、负极暂态电压、电流时域解析值。

典型直流系统参数如表1所示，直流滤波器参数如表2所示。直流线路采用依频架空线模型，长度为1 000 km，根据直流线路的依频参数，可以通过拟合计算得到线路传递函数的相应参数以及高频段稳定的波阻抗，具体参数如表3所示。

表1 高压直流输电系统参数Tab.1 Parameters of HVDC transmission system

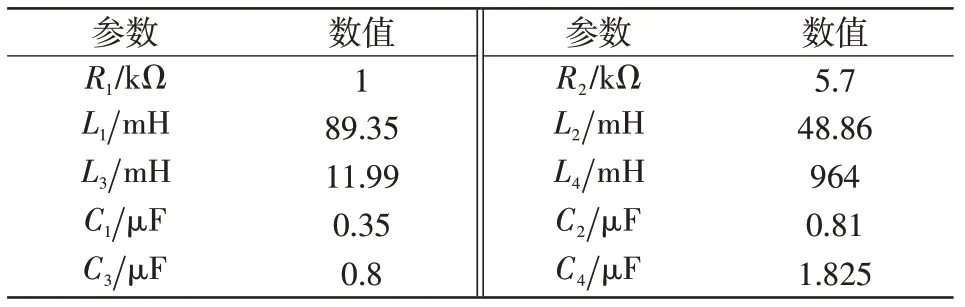
表2 直流滤波器参数Tab.2 Parameters of DC filter

表3 直流线路参数Tab.3 Parameters of DC line

将上述系统参数代入2.1和2.2节解析公式，以直流线路LineMN中点在0 ms时刻发生单极金属性短路故障为例，保护M处的正负极电压uMp(t)、uMn(t)和电流iMp(t)、i Mn(t)的解析结果见附录A。由解析结果表达式可知，对于单极故障，电气量的解析多项式包括1模和0模部分，其延迟函数的延迟时间不同；另外1模和0模部分的多项式各包括1项常数项和多项衰减时间常数不一的衰减项。

3 故障解析计算方法验证及影响因素分析

3.1 故障解析计算方法验证

按图1所示直流系统搭建PSCAD/EMTDC模型，具体参数如表1~表3所示。为了对本文所提故障解析计算方法进行验证，同样以直流线路LineMN中点在0 ms时刻发生单极金属性短路故障为例，将根据第2节解析方法计算所得的解析计算结果与PSCAD模型中进行故障仿真所得仿真结果相对比，保护M处电气量解析结果与仿真结果的对比如图9所示。

根据图8和图9中电气量解析值与所搭建模型仿真值的对比可知，计算所得电气量解析值与仿真值具有较好的吻合特性，上文所提解析方法能够准确计算故障初始阶段的电气量。

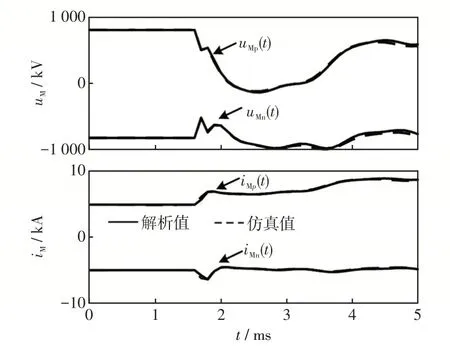
图9 直流线路中点故障情况下的保护M处时域波形Fig.9 Time-domain waveforms at protection position M under DC line midpoint fault

3.2 LCC换流器等值阻抗的影响分析

根据式（1）~（3）可知，计算故障暂态电气量时，LCC换流器等值阻抗选用了综合考虑非换相时期和换相时期下的平均阻抗。为研究换流器等值阻抗对故障解析的影响，图10分别给出了选用非换相期等值阻抗、换相期等值阻抗、平均阻抗以及忽略换流器等值阻抗(ZLCC=0)情况下，保护M处电压、电流的解析计算结果，并与仿真模型的仿真结果相对比。

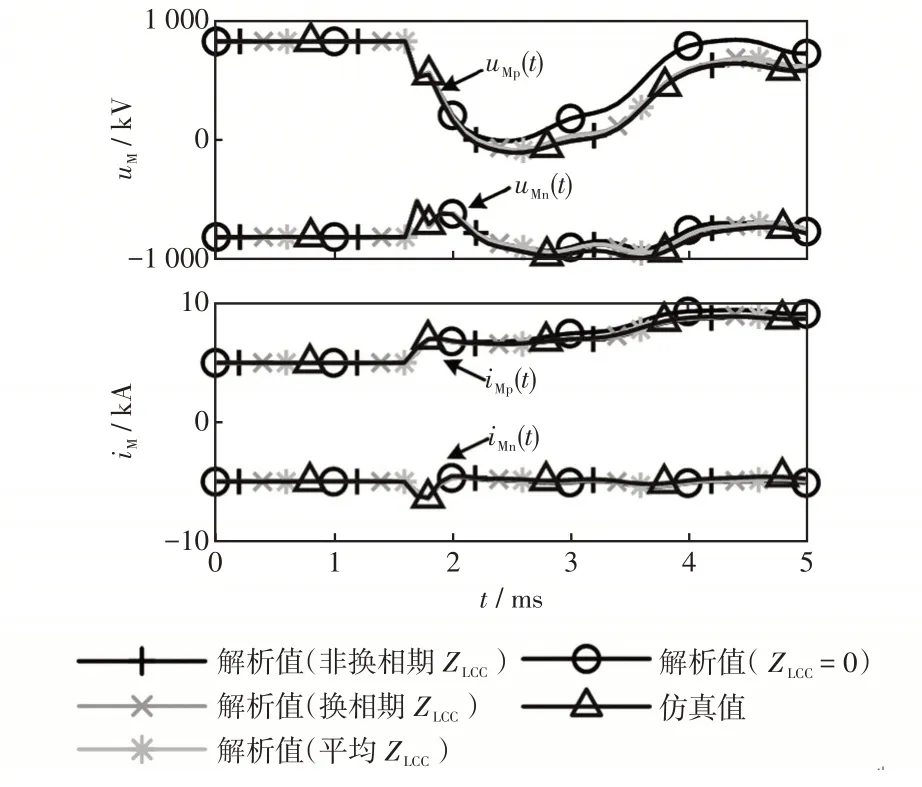
图10 不同LCC等值阻抗下的故障时域波形Fig.10 Time-domain waveforms under fault with various LCC equivalent impedances

由图10可知，不论是选用非换相瞬间还是换相瞬间的换流器等值阻抗，解析计算结果差别很小，都与实际仿真结果相吻合；而在忽略换流器阻抗情况下，解析计算结果与仿真结果出现明显差异，由式（16）可知，忽略换流器阻抗会影响保护处反射系数的准确性，造成首行波计算结果失准。因此，进行故障电气量解析计算时，选用平均等值阻抗作为LCC换流器的计算阻抗符合实际直流系统的故障初始阶段网络结构。

3.3 直流滤波器等值阻抗的影响分析

根据式（5），直流滤波器等值阻抗选用了忽略并联大电阻后的简化阻抗，但该简化阻抗没有降低电路阶数。考虑对直流滤波器进行进一步降阶简化，忽略LC并联支路中的C2、L2、C4、L4，从而得到直流滤波器的简化阻抗为

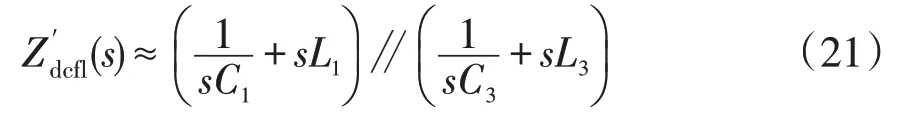
图11给出了直流滤波器分别选用Zdcfl和时保护M处电气量的解析计算结果，并与实际仿真结果相对比。

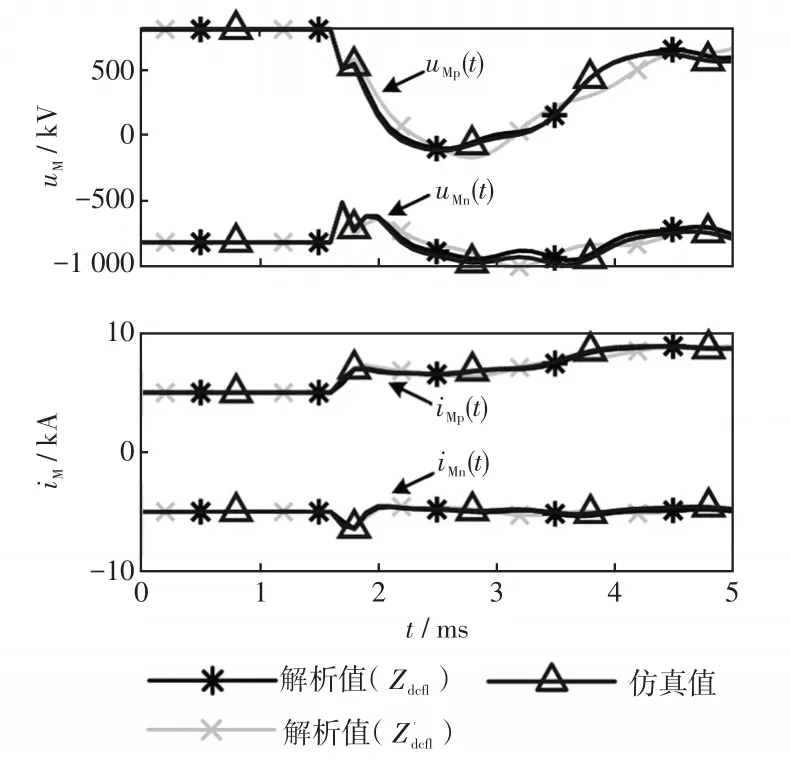
图11 不同直流滤波器等值阻抗下的故障时域波形Fig.11 Time-domain waveforms under fault with various DC filter equivalent impedances

由图11可知，选用忽略并联大电阻后的简化阻抗模型Zdcfl所计算得到的时域解析波形与实际仿真波形在故障初始阶段基本吻合；而选用忽略LC并联支路后的简化阻抗模型所计算得到的时域解析波形与仿真波形有明显的差异。结合式（16）可知，直流滤波器的参数影响了保护处行波的折反射过程，造成了首行波波形的差异，忽略直流滤波器的LC并联支路虽然能有效降低复频域计算的阶数，但使得直流滤波器等值阻抗不再符合故障网络结构，影响了首行波计算的准确性。综上所述，进行故障初始阶段电气量解析计算时，应选用式（5）所示的简化作为直流滤波器的等值阻抗。

4 基于解析解的故障初始阶段暂态电流时域特性分析

本节基于不同情况下计算所得故障初始阶段暂态电流时域解析值波形，对暂态电流的时域特性进行分析，从而可以为直流线路的保护新原理及定值整定研究提供理论依据。

4.1 直流滤波设备对电流时域特性影响分析

1）直流滤波器

有直流滤波器和无直流滤波器时线路末端发生区内和区外单极接地故障时的故障极暂态电流解析计算结果如图12所示。由图12可知，线路区内故障时，直流滤波器严重影响电流时域特征，有直流滤波器时会造成电流波形的振荡，而无直流滤波器时电流波形变得平滑；正向区外故障时，直流滤波器电流时域特征影响不大，电流波形均较为平滑。

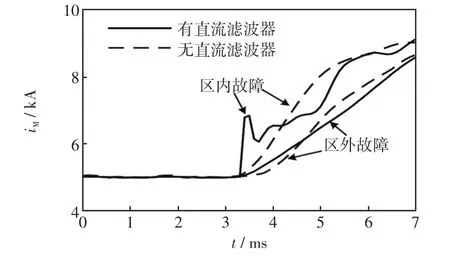
图12 有直流滤波器和无直流滤波器时区内外故障电流解析计算结果Fig.12 Calculation results of current under internal and ex-ternal faults with or without DC filter

2）平波电抗器

有平波电抗器和无平波电抗器时线路末端发生区内和区外故障时的故障极暂态电流解析计算结果如图13所示。由图13可知，线路区内故障时，平波电抗器对于初始电流波动影响不大，初始电流波形均存在波动；正向区外故障时，平波电抗器严重影响电流时域特征，有平波电抗器时会降低高频故障信号，电流波形较为平滑，无平波电抗器时电流波形与区内故障一致，存在波动。即平波电抗器对于正向区内外故障的区分具有重要意义。

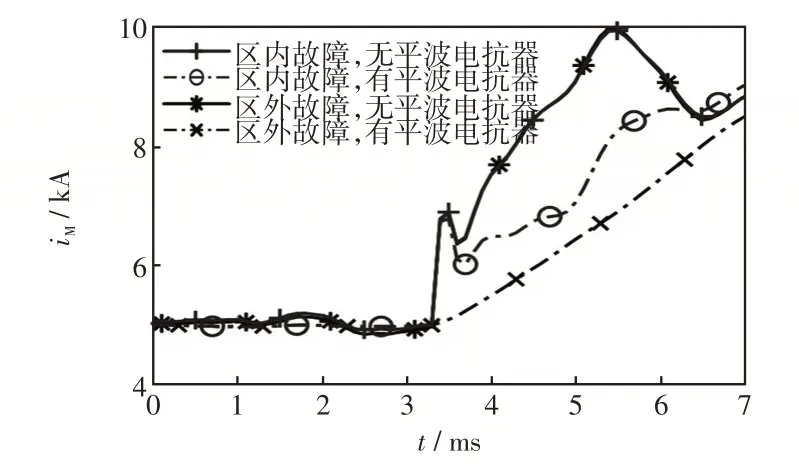
图13 有平波电抗器和无平波电抗器时区内外故障电流解析计算结果Fig.13 Calculation results of current under internal and ex-ternal faults with or without DC reactor

4.2 不同故障条件对电流时域特性影响分析

1）正向区内外故障

直流线路正方向末端发生区内和区外单极接地故障时的故障极暂态电流解析计算结果如图14所示。由图14可知，区内故障时电流波形存在剧烈波动；而区外故障时，由于直流滤波设备的阻滞作用，电流波形较为平缓。对比直流线路正向区内外故障时的电流解析过程，仅有计算故障入射波时所求解的故障点模域网络结构不同，从而造成了故障暂态电流的差异。区外故障时，故障激励源仍需经过平波电抗器和直流滤波器才能在直流线路上产生故障入射波，这对电流的幅值和变化速率都具有明显的衰减作用，因此，区内故障时电流波动程度明显大于区外故障。

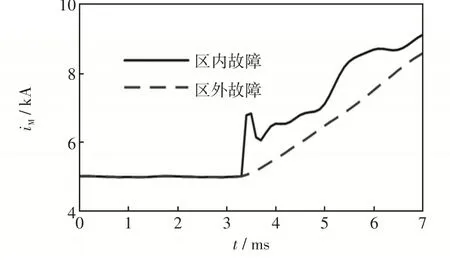
图14 区内外故障下电流解析计算结果Fig.14 Calculation results of current under internal and ex-ternal faults

2）正反向故障

直流线路正方向区外和反方向区外单极接地故障时的暂态电流解析计算结果如图15所示。由图15可知，正方向故障时电流波形突变上升；反方向故障时，电流波形突变下降。因此正反向故障时电流首行波符号相反，即电流突变方向相反。

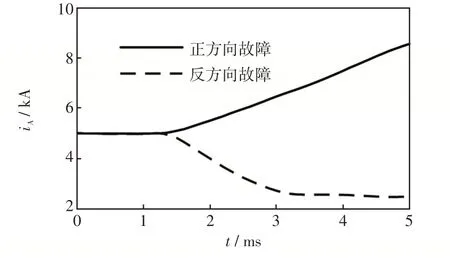
图15 正反向区外故障下电流解析计算结果Fig.15 Calculation results of current under forward and backward external faults

3）本极和另一极故障

正极线路末端和负极线路末端单极接地故障时的正极暂态电流解析计算结果如图16所示。由图16可知，单极故障时，由于耦合作用的影响，非故障极电流也出现了突变量，但故障极电流的变化幅度一般大于非故障极。

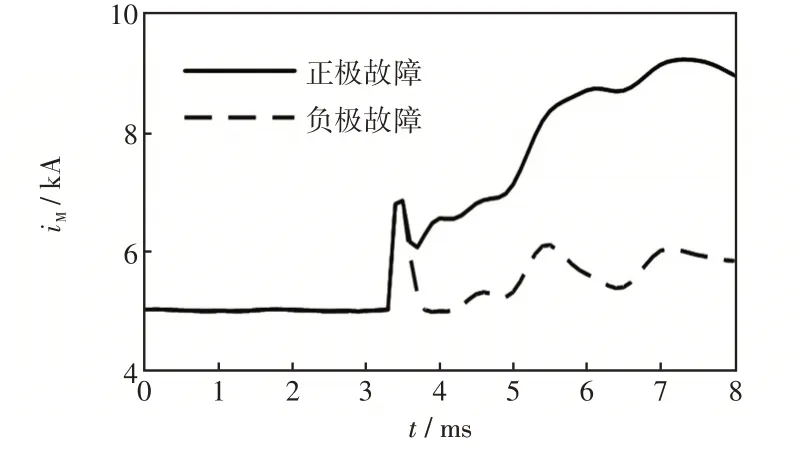
图16 正极和负极故障下正极电流的解析计算结果Fig.16 Calculation results of positive-pole current under posi-tive-and negative-pole faults

4）单双极故障

直流输电线路末端发生双极短路故障和正极接地故障时的正极暂态电流解析计算结果如图17所示。由图17可知，双极短路故障时故障电流变化幅度较单极接地故障更大。

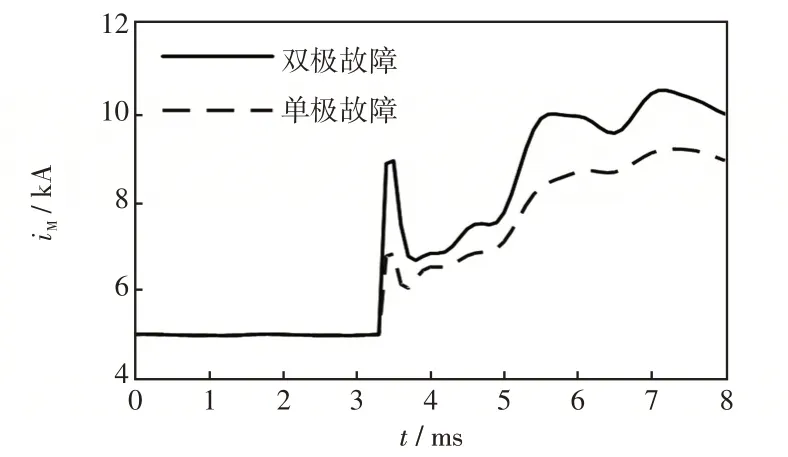
图17 单极和双极故障下电流解析计算结果Fig.17 Calculation results of current under monopolar and bipolar faults

5）不同过渡电阻故障

由2.1节分析可知，过渡电阻直接影响故障点入射波，而不影响行波传递过程以及保护安装处的折反射过程。过渡电阻越大，故障在线路上产生的入射波越小。直流线路区内末端经不同过渡电阻故障（0Ω、100Ω、500Ω、800Ω）及正向区外金属性故障时的故障极暂态电流解析计算结果如图18所示。由图18可知，区内故障过渡电阻越大，暂态电流波形波动程度越小，但波形波动程度总比正向区外故障剧烈。

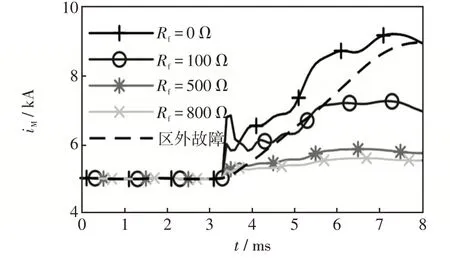
图18 不同过渡电阻故障下电流解析计算结果Fig.18 Calculation results of current under fault with various transition resistances

5 结论

本文针对常规高压直流输电系统，对其直流线路故障初始阶段的时域解析方法进行研究，主要贡献如下。

（1）给出了LCC换流器适用于暂态行波分析的等值模型，形成了用于故障初始阶段分析的直流系统等效电路。提出了用于直流线路故障初始阶段时域解析的通用计算方法，并给出了具体的电气量表达式，经仿真验证，所提故障时域解析方法在有效时间内具有很高的精确度。研究了换流器和直流滤波器等值阻抗、故障位置、控制策略响应对计算结果的影响，确定了不同影响因素下本解析计算方法的精度和时效性。

（2）基于所提解析方法对故障初始阶段暂态电流时域特性进行了系统性分析。经分析，区内故障时电流波动程度明显大于区外故障；正反向故障时电流首行波符号相反，即电流突变方向相反；单极故障时故障极与非故障极电流均出现突变量，但故障极电流变化幅度更大，与非故障极电流变化幅度具有数量级上的差距；双极短路故障时故障电流突变程度约为单极接地故障的2倍；区内故障过渡电阻越大，暂态电流波形波动程度越小，但波形波动程度总比正向区外故障剧烈。

本文所提的故障时域解析方法及由此得到的故障电流解析表达式可以作为直流线路短路故障的行波和频率特性研究的基础，为直流线路的保护新原理及定值整定研究提供了理论依据。

附录A 故障初期电压、电流时域解析结果

以直流线路LineMN中点在0 ms时刻发生单极金属性短路故障为例，保护M处的正负极电压uMp(t)、uMn(t)和电流iMp(t)、iMn(t)的解析结果如式（A1）~（A4）所示：

式中，ε（t）为单位阶跃函数。