基于人工神经网络的双级测量系统定位误差补偿
2022-08-01翁川
翁川
基于人工神经网络的双级测量系统定位误差补偿
翁川
(广东工业大学 精密电子制造技术与装备国家重点实验室,广东 广州 510006)
为解决非接触式高精度传感器量程和精度难以兼容的问题,实现大量程自由曲面的高精度扫描测量,在对国内外测量仪器进行研究分析后,提出一种通过柔性铰链带动高精度传感器跟随曲面实现传感器量程扩展的双级测量系统。为进一步提高该系统的测量精度,采用激光干涉仪对测量系统的定位误差进行标定,利用人工神经网络建立双级测量系统的定位误差模型,然后利用该模型进行定位误差补偿,以求尽可能地消除测量系统的系统误差,随后使用激光干涉仪再次对定位误差进行测量,测量结果和作为传统定位误差补偿方法的补偿表补偿法进行对比,最终发现定位精度大大提高,证明了基于人工神经网络的定位误差的优越性。
人工神经网络;扫描测量;定位精度
非接触式传感器在精度和量程之间存在矛盾,高精度传感器量程往往较小,如光谱共焦传感器、电容传感器等传感器往往只具有几十到上百微米的量程,难以进行高低差较大曲面的高速扫描测量[1]。针对这个问题,计划利用音圈电机驱动柔性铰链结构带动高精度传感器做直线位移,在扫描测量过程中跟随被测表面,实现传感器的量程扩程。该测量方案中,使用光栅尺作为柔性铰链的反馈控制装置,同时也对柔性铰链的位移进行测量,作为二级测量系统,而安装在柔性铰链上的高精度传感器作为一级测量系统。为进一步提高测量系统精度,计划对双级测量系统的定位误差进行补偿,以消除测量系统的系统误差。
在传统工业控制中,若仅通过电气控制系统和硬件结构来保证精度,成本会随着精度的提高呈指数式增长[2]。因此,在将电气控制系统和硬件结构精度提高到一定程度后,一般通过定位误差补偿来实现更高的定位精度[3-4]。常用的定位精度补偿方法有线性回归模型、多项式拟合模型、神经网络模型等[5]。目前,已有许多学者利用神经网络模型进行了传统机床定位误差补偿研究。John M. Fines等[5]和Prakash Vinod等[6]利用神经网络模型对机床定位误差进行建模,并将补偿模型集成到机床控制系统中,实现机床的定位误差补偿。
由于柔性铰链在整个运动行程内刚度并非恒定不变,而呈现一种非线性关系、难以用一个准确的数学模型进行误差分析,因此拟合的精度往往不够理想。但是,人工神经网络模型不需要考虑模型的物理意义,可以通过自我学习而实现良好的非线性拟合,非常适合用来建立柔性铰链的定位误差模型。
基于以上分析,本文通过激光干涉仪对二次测量系统的定位精度进行测量,并利用人工神经网络模型进行双级测量系统定位误差模型的建立,以此模型进行定位补偿,消除测量系统的系统误差,同时运用传统的定位误差补偿方法——补偿表法进行补偿,对比两次补偿结果,用以验证基于人工神经网络的定位误差补偿的效果。
1 双级测量系统
如图1所示,提出一种双级测量系统,通过在扫描测量过程中移动高精度传感器来实现曲面跟随,使工件在测量过程中始终保持在传感器量程范围内,以此实现高低差较大曲面的扫描测量。该双级测量系统主要分为驱动装置和执行装置。

图1 双级测量系统
驱动装置作为系统的动力装置,选用音圈电机。这是因为音圈电机能实现无限分辨率的直线运动,同时有具有结构简单、体积小、重量轻、响应快、行程大等特性[7],有利于提升测量装置的精度、减小测量装置的体积,使得测量装置在尽可能保持紧凑、简洁的同时,还能实现所需的高精度大量程测量。
音圈电机选型时,需要确定的参数包括电机的行程、峰值力和持续力,并尽可能选用体积较小的电机。其中,电机行程根据测量装置性能要求选择,本文测量装置行程为5 mm,该行程基本满足了大部分曲面测量的需求。确定音圈电机的持续力和峰值力时,假定整个运动周期是频率1 Hz、峰值2.5 mm的一个正弦运动。峰值力计算为:
F=F+F+F(1)
式中:F为音圈电机所需峰值力,N;F为载
荷力,包括刀尖所受的切削力等,N;F为摩擦力,N;F为运动部分的惯性力,N。
持续力计算为:

式中:F为音圈电机所需持续力,N;1为加速运动时间,s;2为匀速运动时间,s;3为减速运动时间,s;4为运动过程的延时时间,s。
为提高可靠性,所选音圈电机应稍大上述行程、峰值力和持续力需求。
执行装置用于携带高精度传感器进行位移,是整个二级测量装置的核心机构,选用三级复合柔性铰链来完成该功能。它能在限制其他方向自由度的同时,利用柔性铰链的高重复性和高定位精度,实现一个高精度的直线位移,同时采用复合柔性铰链的方式,将多级柔性铰链串联以扩大柔性铰链的行程,并采用对称结构,抑制寄生运动的出现[8],最终实现大行程且高精度的直线位移。
驱动控制方面,该双级测量系统采用工控机作为上位机、UMAC控制器作为下位机的控制模式,并通过线性驱动器A330驱动音圈电机,再由雷尼绍公司的增量式光栅尺对柔性铰链的位移进行测量,并反馈给UMAC控制器,实现全闭环控制,光谱共焦传感器则通过以太网将测量数据传输给上位机。其控制系统如图2所示。
该双级测量系统的工作模式为:在光谱共焦传感器量程范围内设置一个工作区间,将该区间定为安全范围,这是防止工件超出光谱共焦传感器量程从而导致测量中断所预留的余量。扫描测量过程中,一旦测量工件超过该范围,则控制系统驱动音圈电机带动柔性铰链和光谱共焦传感器进行运动,使工件回到设定的安全范围内。另外,作为伺服反馈的增量式光栅尺也作为第二级测量系统测量柔性铰链的位移,最终结合光谱共焦传感器的数据和光栅尺的数据便可获得测量工件的表面轮廓信息。通过这种二级测量的方式,在对高低差较大曲面进行扫描测量时,高精度传感器会跟随曲面进行运动,使工件从始至终保持在传感器量程范围内,从而完成对曲面的测量。

图2 双级测量系统控制系统框图
因此,提高带动传感器运动的柔性铰链位移机构的定位精度,是提高测量装置精度的关键所在。在结构硬件已经确定的情况下,想进一步提高定位精度,最有效的方法便是进行定位误差的补偿。
2 基于人工神经网络的定位误差模型建立
传统的定位误差补偿的方式是运用补偿表进行补偿,通过激光干涉仪等外部高精密设备获得运动系统各个等间隔位置的定位误差数据,再通过设置控制系统内置补偿表的数据,在运动系统每次到达指定位置进行补偿,从而提高系统定位精度。这在简单的线性运动系统中是一种有效的方法,但在复杂的非线性系统中,补偿表方法很难保证足够的补偿精度。
基于前面的分析,本文计划通过激光干涉仪对双级测量系统的定位误差进行测量,确定柔性铰链位移机构的定位误差,基于所测得的双级测量系统的定位误差数据,利用人工神经网络模型对系统定位误差进行建模,以此代替补偿表进行定位误差补偿,提高系统定位精度,使之具备大量程超精密扫描测量能力。
人工神经网络是对生物神经网络的一种模仿,特别是对人脑神经元网络进行抽象,通过一些特定的节点相互联结构成,每个节点代表一种特定的输出函数,这些函数被称为激励函数[9]。同时,节点相连间还有一个加权值,是人工神经网络学习的一个重要参数。通过并行运行,信息输入同一层的节点然后输出,之后将输出值进一步传入下一层神经元。由于其自适应性,人工神经网络在机械加工制造中有许多应用,江景涛等[9]进行了车身零件检具概念设计的相关研究。本文采用的神经网络模型为BP(Back Propagation,反向传播)神经网络,该模型是1986年由Rumelhart和McClelland为首的科学家提出的概念,是一种按照误差逆向传播算法训练的多层前馈神经网络,是应用最广泛的神经网络模型之一[10]。采用有监督的BP神经网络模型,其是对模型输入训练集,可以根据理论输出和实际输出的误差作为判断标准和反馈,以此对连接权值进行调整的学习方法。从而实现二级测量系统的定位误差模型建立。
3 定位精度测量补偿实验
双级测量系统的定位精度补偿实验可分为以下步骤:
(1)安装调试好激光干涉仪,对双级测量系统的定位误差进行测量并采集足够的数据;
(2)以获得的数据进行补偿表定位误差补偿作为结果对比;
(3)设计神经网络模型并利用采集的数据对该模型进行训练,获得双级测量系统的定位误差模型;
(4)利用获得的定位误差模型对双级测量系统进行补偿,继续使用激光干涉仪测量系统定位误差;
(5)对比两次补偿效果,验证利用人工神经网络模型进行补偿是否具备超过传统补偿表补偿的补偿精度。
安装调试激光干涉仪的方法为:首先架设激光头,这是发射激光和接收反射激光的组件,需将其固定于三脚架,并完成调平工作。然后在柔性铰链位移机构上安装反射镜,并进行微调,将入射激光反射到激光头接收激光口处,随后调整激光头角度和位置,保证所发射的激光与二级测量系统的柔性铰链位移机构的运动方向一致。调整方法是在激光头对应位置安装指示片,通过口诀“来拒去留”完成调试,保证柔性铰链位移机构在全行程内都能将入射激光准确反射到激光头激光接收口处。最后是安装分光镜,安装在激光头和反射镜中间的固定位置,用于将入射光分为两束,一束不改变方向继续往原路径射到反射镜上,另一束翻转90°往上走经分光镜上的反射镜原路由分光镜再一次翻转90°和反射激光重合,射向激光头激光接收口处。安装调试完成的激光干涉仪测量系统如图3所示。

图3 定位误差测量实验
所设计的双级测量系统需进行补偿的范围为-2.5~2.5 mm,计划在此区间内每隔0.5 mm测量一个点的数据,总计11个点,每次实验正负方向各进行一次,共进行10次实验。通过UMAC控制器的上位机软件可以进行编程,控制柔性铰链机构安装上述测量方法运动,即在-2.5~2.5 mm的行程方位内运动,每次到达指定位置,也就是测量点位置便停留5 s,方便激光干涉仪采集数据。同时激光干涉仪按照实验需求进行设置,每次检测到测量物体到达指定位置停留时就会采集数据,并进行数据处理,包括整体定位精度、正负方向的定位精度、整体重复性、正负方向的重复性的计算。实验结果如图4所示,该系统在全行程范围内的定位精度为8.482 μm,正方向的定位误差8.48 μm,负方向8.42 μm,这在高精度测量中是不能接受的,但是实验结果表现出很好的重复性,其值为0.45 μm,在正方向的重复性达到0.32 μm、负方向达到0.40 μm,达到了作为补偿表补偿依据和神经网络模型训练集的基本条件。
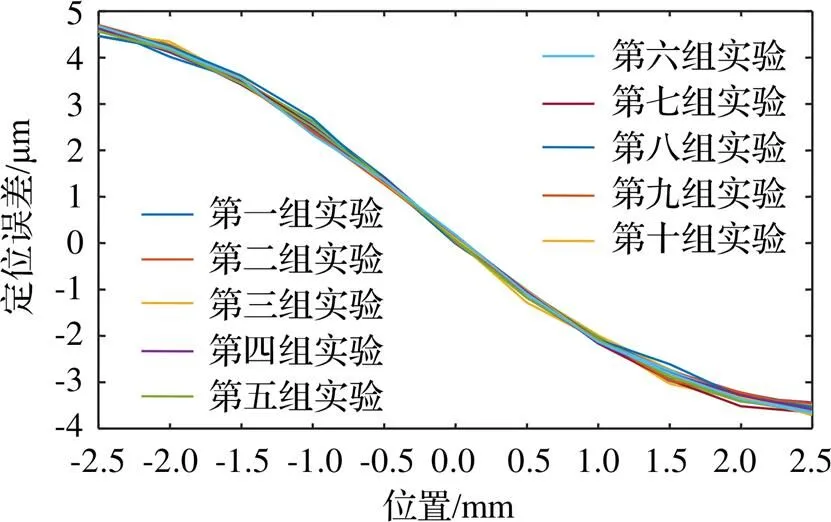
图4 二级测量系统原始定位误差
首先利用这些数据进行补偿表定位误差补偿。常用的控制器基本在具备补偿表补偿功能,UMAC控制器也不例外。
补偿步骤如下:
(1)将激光干涉仪测得的定位误差数据按要求排列好;
(2)将所有数据的误差减去作为参考点的零点的误差;
(3)按指定的单位转换公式将数据转换成控制器所需的值,获得补偿表;
(4)将补偿表数据按格式填入编辑窗口,并下载补偿表到控制器里,可利用指令LIST BLCOMP查看补偿表;
(5)最后利用UMAC的i指令I51=1开启补偿表补偿功能。
开启补偿表功能后,按照前述方法再次进行定位误差测量,不过这次为了验证测量结果,将采集间隔改为0.25 mm,即总共测量21个点,其他设置不变,测量结果如图5所示,全行程范围的定位精度降低到0.731 μm,其中,正方向定位精度为0.707 μm,负方向定位精度为0.596 μm。可以看出,定位精度虽有所提升,但仍未达到第一次重复性的精度。

图5 补偿表补偿结果
进行基于人工神经网络的定位误差补偿时,首先是对神经网络模型进行训练和测试,从而确定所需的二级测量系统定位精度模型。基于MATLAB里的newff函数可建立有监督的BP神经网络模型。要用该函数进行网络训练,首先需对数据进行归一化处理,利用MATLAB的mapminmax函数对训练集数据进行归一化处理,目的是使数据范围变小、减小训练时间,同时避免训练集的输出数据超过激活函数的值域。随后是确定神经网络模型的各个参数,包括网络层数、各层神经元个数、激活函数和训练函数等。在经过多次尝试后,发现当采用训练层数为3,各层神经元个数分别为6、10、1,tansig激活函数和默认的l m训练函数时,能较快实现最小误差为1E-10 mm的神经网络模型训练,训练结果如图6所示。
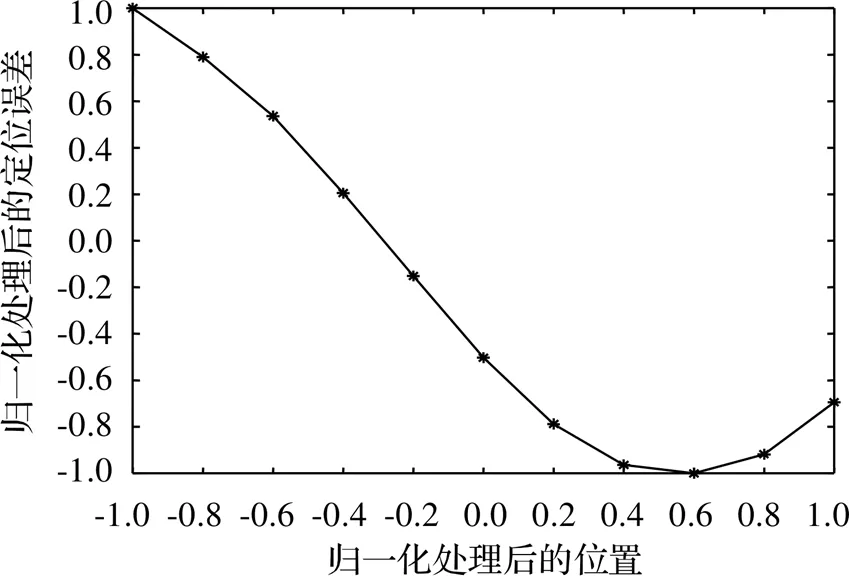
图6 神经网络模型训练结果
获得满足精度要求的定位误差模型后,根据这个模型对双级测量系统的定位误差进行补偿。补偿方法为,在控制上位机每次向伺服控制系统发送位移指令时,调用该模型输出一个补偿值,然后用该补偿值对位移指令进行补偿作为最终的位移指令控制电机运动。为验证补偿效果,再次利用激光干涉仪对补偿完的双级测量系统进行定位误差测量。同样的,由于训练集是在全行程5 mm、每隔0.5 mm进行取样,为提高实验结果可信度,此次实验采集间隔取0.25 mm,即总共测量21个点,其他设置不变。经过补偿后的测量结果如图7所示,可知,全行程范围的定位精度降低到0.464 μm,其中,正方向定位精度为0.401 μm,负方向定位精度为0.464 μm,定位精度大幅度提高,基本和系统重复性持平,说明经补偿后双级测量系统的系统误差基本消除,剩下大部分为随机误差[11],对比利用补偿表补偿的结果也可看出整体的补偿精度大幅度提升,证明了基于人工神经网络的定位误差补偿方法的优越性。
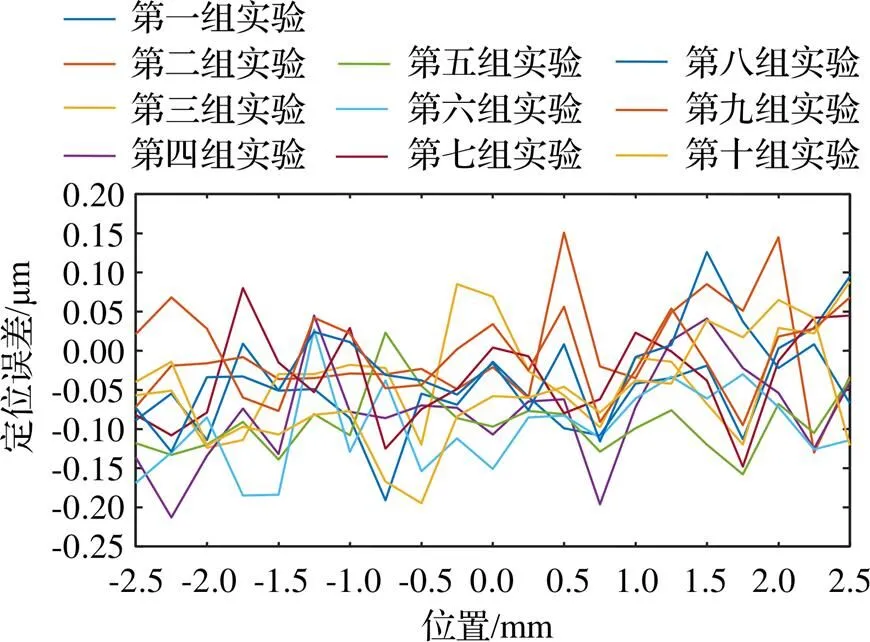
图7 神经网络模型补偿结果
4 结论
提出一种用于大量程自由曲面扫描测量的双级测量装置,为提高该装置的定位精度,使用激光干涉仪对该装置的定位误差进行测量,获得定位误差数据,先将该数据作为传统的补偿表的依据进行补偿表补偿,随后将这些数据作为训练集进行BP神经网络模型的训练,获得双级测量系统的定位误差模型,最终以此模型对双级测量系统的定位误差进行补偿。再次使用激光干涉测量补偿后的定位误差,测量结果表明,基于人工神经网络的补偿的定位精度从8.482 μm降低到0.464 μm,相比补偿表法有较大的提升,证明了基于人工神经网络模型的定位误差补偿法的优越性。
[1]Cacace L A. An optical distance sensor:tilt robust differential confocal measurement with mm range and nm uncertainty[D]. Netherlands:Eind-hovenUniversityofTechnology,2009.
[2]林健,汪木兰,李宏胜. 基于遗传神经网络的直线伺服系统定位误差补偿[J]. 组合机床与自动化加工技术,2011(2):86-88.
[3]Koay C A,Srinivasan D. Particle swarm optimization-based approach for generator maintenance scheduling[C]. Swarm Intelligence Symposium. IEEE,2003.
[4]Gaing Z L. A particle swarm optimization approach for optimum design of PID controller in AVR system[J]. IEEE Transactions on Energy Conversion,2004,19(2):384-391.
[5]Fines J M,Agah A. Machine tool positioning error compensation using artificial neural networks[J]. Engineering Applications of Artificial Intelligence,2008,21(7):1013-1026.
[6]Vinod P,Narendra R T,Kumar S. Real-time Positioning Error Compensation for a Turning Machine Using Neural Network[C]. ICAMME-2014. 2014.
[7]张大卫,冯晓梅. 音圈电机的技术原理[J]. 中北大学学报(自然科学版),2006,27(3):224-228.
[8]Xu Q. Design, testing and precision control of a novel long-stroke flexure micropositioning system[J]. Mechanism and Machine Theory,2013,70(6):209-224.
[9]江景涛,隋仁东,胡彩旗. 基于神经网络的车身零件检具概念设计[J]. 机械,2007,34(7):3.
[10]闻新.应用MATLAB实现神经网络[M]. 北京:国防工业出版社,2015:95
[11]李圣怡. 精密和超精密机床精度建模技术[M]. 长沙:国防科技大学出版社,2008.
Positioning Accuracy Compensation of a Secondary Measurement System Based on Artificial Neural Network
WENG Chuan
( State Key Laboratory of Precision Electronic Manufacturing Technology and Equipment, Guangdong University of Technology, Guangzhou 510006, China )
In order to solve the problem that the range and precision of the non-contact high-precision sensor are difficult to be compatible and realize the high-precision scanning measurement of the large range free-form surface, after the research and analysis of measuring instruments at home and abroad, a dual-level measurement system is proposed to expand the sensor range by driving the high-precision sensor to follow the surface through the flexible hinge. In order to further improve the measurement accuracy of the system, the laser interferometer is used to calibrate the positioning error of the measurement system. And the artificial neural network is used to establish the positioning error model of the secondary measurement system, and then the model is used to compensate the positioning error so as to eliminate the system error of the measurement system as much as possible. And then the laser interferometer is used to measure the positioning error again. At the same time, it is compared with the compensation table compensation method which is considered as the traditional compensation method of positioning error. As the result, it is found that the positioning accuracy is greatly improved, which proves the superiority of the positioning error compensation based on artificial neural network.
artificial neural network;scanning measurement;positioning accuracy
TP212
A
10.3969/j.issn.1006-0316.2022.07.012
1006-0316 (2022) 07-0075-06
2021-12-06
翁川(1996-),男,广东汕头人,硕士,主要研究方向为高精密测量,E-mail:644827901@qq.com。
