地铁车辆转向架构架模态匹配方法研究
2022-08-01董晓华吴兴文赵明花梁树林李飞
董晓华,吴兴文,赵明花,梁树林,李飞
地铁车辆转向架构架模态匹配方法研究
董晓华1,吴兴文*,2,赵明花3,梁树林1,李飞1
(1.西南交通大学 牵引动力国家重点实验室,四川 成都 610031;2.西南交通大学 机械工程学院,四川 成都 610031;3.国家高速列车青岛技术创新中心,山东 青岛 266000)
首先调研了地铁线路不同轨道类型轮轨耦合振动特性,以及不同曲线半径、不同轨道类型下钢轨波磨波长的分布状态,进一步结合构架固有模态信息对车辆轨道系统模态静态匹配展开研究;然后基于刚柔耦合理论和模态综合法建立了考虑构架柔性的地铁车辆刚柔耦合动力学模型,通过扫频法对车辆轨道系统模态动态匹配展开研究;最后分析构架结构阻尼比和转向架一系悬挂垂向刚度对构架振动传递的影响。针对以上研究,提出了一套适用于地铁转向架的模态匹配方法,进一步识别了转向架构架上可能出现的共振区段以及敏感的工作模态。
模态分析;刚柔耦合动力学模型;模态静态匹配;模态动态匹配;结构阻尼比
随着地铁车辆运营里程的增加,转向架构架出现了诸多由结构共振导致的失效案例,张富兵等[1]通过线路跟踪试验发现,由于钢轨波磨通过频率与轮对安全吊固有模态频率接近,导致安全吊发生结构共振破坏。董磊等[2]针对某型城轨车辆动力转向架进行线路动应力测试和可靠性评估,发现电机吊座与横梁连接处发生了明显的弹性共振,引起共振的原因是外界激扰(车轮缺陷、轨缝冲击和线路不平顺)与构架固有模态接近。韩博[3]通过频域法分析实测动应力与加速度数据,发现来自构架端部的加速度激励激发了天线梁固有模态,使得天线梁在车辆运行中发生结构共振,导致开裂失效。连青林等[4]通过线路实测试验对客车转向架安全吊座孔附近疲劳裂纹展开研究,结果表明,受线路激扰影响,安全吊杆第四阶固有模态被激发产生结构共振,导致产生疲劳裂纹,最后针对安全吊杆进行结构改进与优化,优化后的结构满足使用要求。瞿邵奇等[5]基于Dirlik经验公式和Miner线性累计损伤原则,从频域法的角度评估某飞行器径向连接螺栓的振动疲劳寿命,发现螺栓断裂原因为低频结构共振。石怀龙等[6]基于有限元法和线路试验对地铁车辆转向架轴箱吊耳断裂问题展开研究,结果表明,车辆以常用速度通过波长为61.5 mm的钢轨波磨时,与吊耳一阶固有模态发生模态共振,振动响应激增,最终发生断裂。
由此可见,地铁转向架大量的疲劳失效主要是结构的模态共振导致。现有的模态匹配设计还存在不足,未能准确预测出结构可能被激发的工作模态,故需要提出一种新的模态匹配方法。在结构设计之初能更加全面地识别出可能被激发的共振模态,从而减少结构振动疲劳问题。以往的模态匹配大多为模态频率的规划,只给出线路固有激扰频率与构架固有模态频率分布,不能得出哪些模态容易被激发。为此,吴兴文等[7]提出一种基于刚柔耦合的模态动态匹配方法,并成功运用于高速列车车体的模态匹配和振动疲劳研究。
经验表明,地铁车辆的运营线路条件相比高铁更加复杂,一条线路存在多种轨道结构,轮轨激励频率十分丰富,因此针对地铁车辆转向架的模态动态匹配尤为重要。本文针对地铁转向架模态匹配,首先调研现有轨道系统主要的固有轮轨耦合模态与钢轨波磨特征,分析轨道系统与构架可能的共振频带。然后,基于考虑构架柔性的地铁车辆刚柔耦合动力学模型,开展转向架构架模态动态匹配研究,识别构架敏感的工作模态,同时分析不同服役模式下转向架悬挂参数对转向架高频振动特性的影响。
1 地铁车辆服役边界条件
1.1 轮轨耦合振动特性
在进行模态静态匹配之前,首先要充分了解地铁车辆的服役边界,尤其是轮轨相互作用。轮轨相互作用的定义是,外部激励作用下轮对和轨道的耦合振动行为。轮轨耦合振动最主要的表现形式有:P2力轮轨耦合共振、轮对间钢轨的弯曲模态、轮轨之间的反共振、钢轨pine- pine弯曲模态等。
P2力轮轨耦合振动是车辆轨道系统中低阶轮轨耦合振动模态,表现为车轮和钢轨的同向浮沉运动,是导致地铁车轮多边形磨耗和钢轨波磨的主要原因之一,频率一般在30~100 Hz,能够充分地向车上及轨下传递,造成车辆系统异常振动和轨道基础结构破坏[8]。除了低阶次P2力轮轨耦合振动外,车辆轨道系统也存在高阶次轮轨耦合振动,例如转向架两个轮对间的钢轨局部弯曲模态等[9]。
轮轨耦合振动频率主要与轨下支撑刚度、钢轨弯曲刚度、车轮质量和钢轨质量有关。我国地铁线路包含普通短轨枕、弹性短轨枕、浮置板轨道、单趾弹簧扣件、GJ-III型扣件、先锋扣件等多种轨道类型。不同的轨道类型其参数差异较大,因此导致的轮轨之间耦合振动存在一定差异。
通过对大量文献[10-16]的调研,可知不同轨道类型轮轨耦合振动特性复杂多变,P2共振频率为20~80 Hz,钢轨一阶、二阶、三阶弯曲模态依次为180 Hz左右、350 Hz左右、556 Hz左右。轮轨耦合振动频率范围从P2共振中低频率到轮对间钢轨弯曲模态高频率都有覆盖,极易引发转向架系统模态共振问题。
1.2 钢轨波磨分布特征
由于钢轨波磨与轮轨之间的耦合振动特性具有较大相关性,因此不同轨道结构的钢轨波磨特征也存在较大出入。本节基于广州某线路实测波磨数据得到了不同轨道类型在不同曲线半径下钢轨波磨分布状态,如表1所示。
当地铁车辆以某一运营速度通过波磨区段时,轮轨间极易产生高频载荷,这些高频载荷经一系悬挂系统传递至转向架主体及其附属部件,极易引起转向架的结构模态共振,从而严重影响转向架的疲劳寿命,因此需要计算波磨通过频率,计算公式为[17]:
=/(1)
式中:为波磨通过频率,Hz;为车速,km/h;为波磨波长,mm。
以科隆蛋扣件为例,钢轨波磨波长为180~200 mm,当车辆以常用运营速度(60 km/h)通过波磨区段线路时,计算得:≈83~93 Hz
同理可得不同轨道类型下钢轨波磨的通过频率分布状态,如图1所示。可知,钢轨波磨通过频率主要集中在53~167 Hz、167~265 Hz以及333~538 Hz三个频带内。

表1 不同轨道类型在不同曲线半径下钢轨波磨波长分布状态[17]
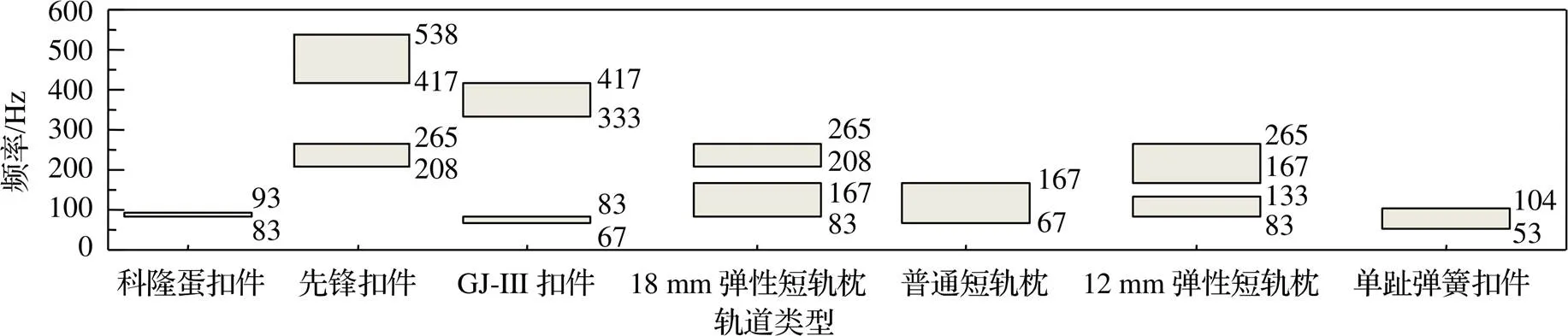
图1 不同轨道类型下钢轨波磨通过频率分布状态
2 构架模态静态匹配研究
轮轨耦合振动频率和钢轨波磨通过频率都极有可能激发构架模态,引起系统结构共振。基于此,本小节结合构架固有模态首先展开构架模态静态匹配研究,识别可能存在的共振区间。转向架构架的模态是通过ANSYS软件BlockLanczos方法获得。在本文的研究中考虑了构架300 Hz以内的模态,如表2所示。

表2 构架有限元仿真模态
根据前文总结的不同轨道类型轮轨耦合振动频率和钢轨波磨通过频率,结合构架固有模态进行模态静态匹配研究,如图2所示。可知,频率在37~41 Hz时,容易与构架扭转模态发生共振;频率在54~167 Hz时,容易与构架侧梁横向弯曲模态、构架侧梁垂向弯曲模态以及构架侧梁端部摆动模态发生共振;频率在167~265 Hz时,容易与转向架构架侧梁端部摆动模态、构架端部纵向摆动模态以及构架侧梁和端部耦合模态发生共振。
从图2虽然可以看出在工作模态范围内哪些地方存在明显的共振区间,但回答不了哪些工作模态容易被激发,以及共振幅值到底有多大的问题。为进一步识别构架在典型工况下敏感的工作模态以及共振幅值,下面通过考虑构架柔性的刚柔耦合动力学模型,开展典型服役工况下的构架模态动态匹配研究,进一步识别典型运营条件下转向架构架的工作模态。

图2 构架模态静态匹配
3 地铁车辆刚柔耦合动力学模型
地铁车辆在实际服役过程中,既要承受来自车体的低频载荷,又要承受钢轨波磨等不平顺导致的高频激扰,而传统的多刚体动力学模型只能仿真再现构架受到的一些低频载荷特性,不能考虑钢轨波磨等一些高频激励引起的构架结构共振问题。为此,本文基于大系统刚柔耦合动力学理论和模态综合法建立考虑构架柔性的地铁车辆刚柔耦合模型,如图3所示。
为了考虑构架服役过程中的弹性振动,使用模态综合法将构架考虑为柔性。
相对于构架参考坐标系,有[9]:
(,)=+(,) (2)
式中:为构架上任意点的位置坐标;(,)为点位置的弹性振动响应;(,)为点位置的弹性振动。
根据模态叠加法,有[9]:
(,)=() (3)
式中:为模态矩阵;()为构架各阶模态正则坐标。
根据模态应力恢复法,有[9]:
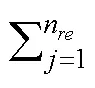
式中:为弹性振动导致的节点应力,MPa;n为模态应力恢复法中考虑的模态数目;σ为第阶模态应力,MPa;q为第阶模态坐标。
在本文的研究中,构架考虑了300 Hz以内的柔性模态,模型中转向架构架的典型模态振型如图4所示。

图3 刚柔耦合动力学模型

图4 转向架构架典型模型振型
由于本文主要关心转向架在各种轮轨激励下的模态响应,因此本文基于地铁转向架刚柔耦合动力学模型建立了适用于模态匹配的扫频模型,如图5所示。扫频模型简化了刚柔耦合动力学模型的轮轨关系,直接采用点到点大刚度力元进行模型,不考虑轮轨之间的蠕滑。

图5 构架刚柔耦合扫频模型
模型通过驱动大刚度力元的移动Marker点来实现轮轨系统的扫频激励。在本文的研究中,轮轨之间的扫频激励范围为0~350 Hz,主要模拟转向架构架浮沉、侧滚、点头和扭转等服役状态,如表3所示。
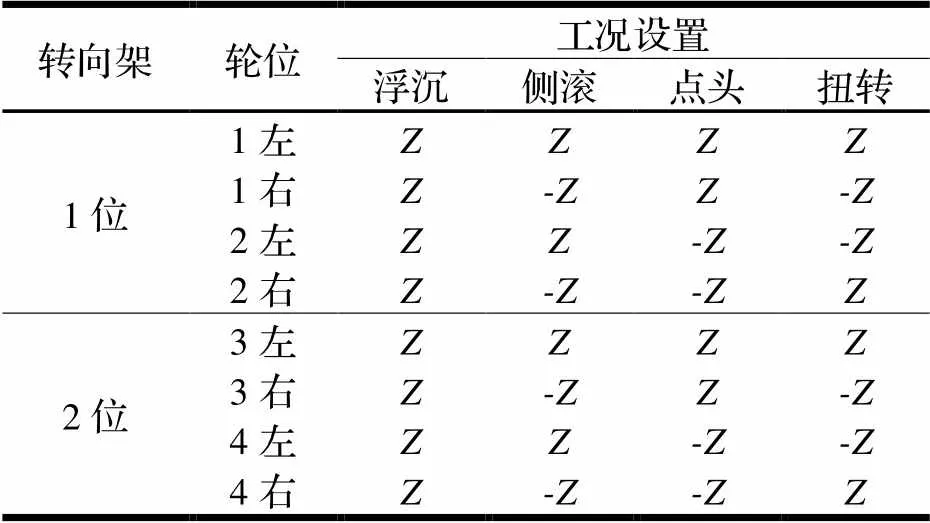
表3 扫频激励工况设置
注:表示垂直向下;表示垂直向上。
4 构架模态动态匹配研究
基于以上刚柔耦合动力学扫频模型,本文主要研究在转向架典型服役工况下,结构阻尼比和悬挂参数对转向架构架典型位置振动传递的影响,以进一步识别转向架构架的工作模态。
4.1 结构阻尼比对构架振动响应的影响
基于以上各种扫频激励模式,获得了各个扫频模式下构架关键部位的振动响应,本文通过选取构架横梁、轴箱上方构架和构架端部三个关键位置对构架的工作模态进行研究。
浮沉扫频激励下三个典型关键位置的加速度频谱图如图6所示。
可知,浮沉激励模式下,转向架构架主要表现主频为114.5 Hz、133.9 Hz、224.4 Hz等模态,表明在相同激励水平下这些模态频率更容易被激发。其中,133.9 Hz为构架侧梁反向一阶垂弯模态,156.4 Hz为构架侧梁同向二阶垂弯模态,224.4 Hz和236.0 Hz为构架端部局部纵向摆动模态。结合不同轨道类型轮轨耦合振动频率和钢轨波磨通过频率可知:133.9 Hz模态容易在18 mm弹性短轨枕、普通短轨枕和 12 mm弹性短轨枕线路被轮轨高频激励激发;156.4 Hz模态容易在18 mm弹性短轨枕和普通短轨枕线路被轮轨高频激励激发;224.4 Hz和236.0 Hz模态容易在减振型扣件、18 mm弹性短轨枕和12 mm弹性短轨枕被轮轨高频激励激发。另外,相比构架横梁和轴箱正上方侧梁,构架端部振动加速度响应明显大于其他部位,说明其实际服役情况下更容易表现出模态共振现象。研究同时表明,133.9 Hz和224.4 Hz模态响应受结构阻尼比影响较大。
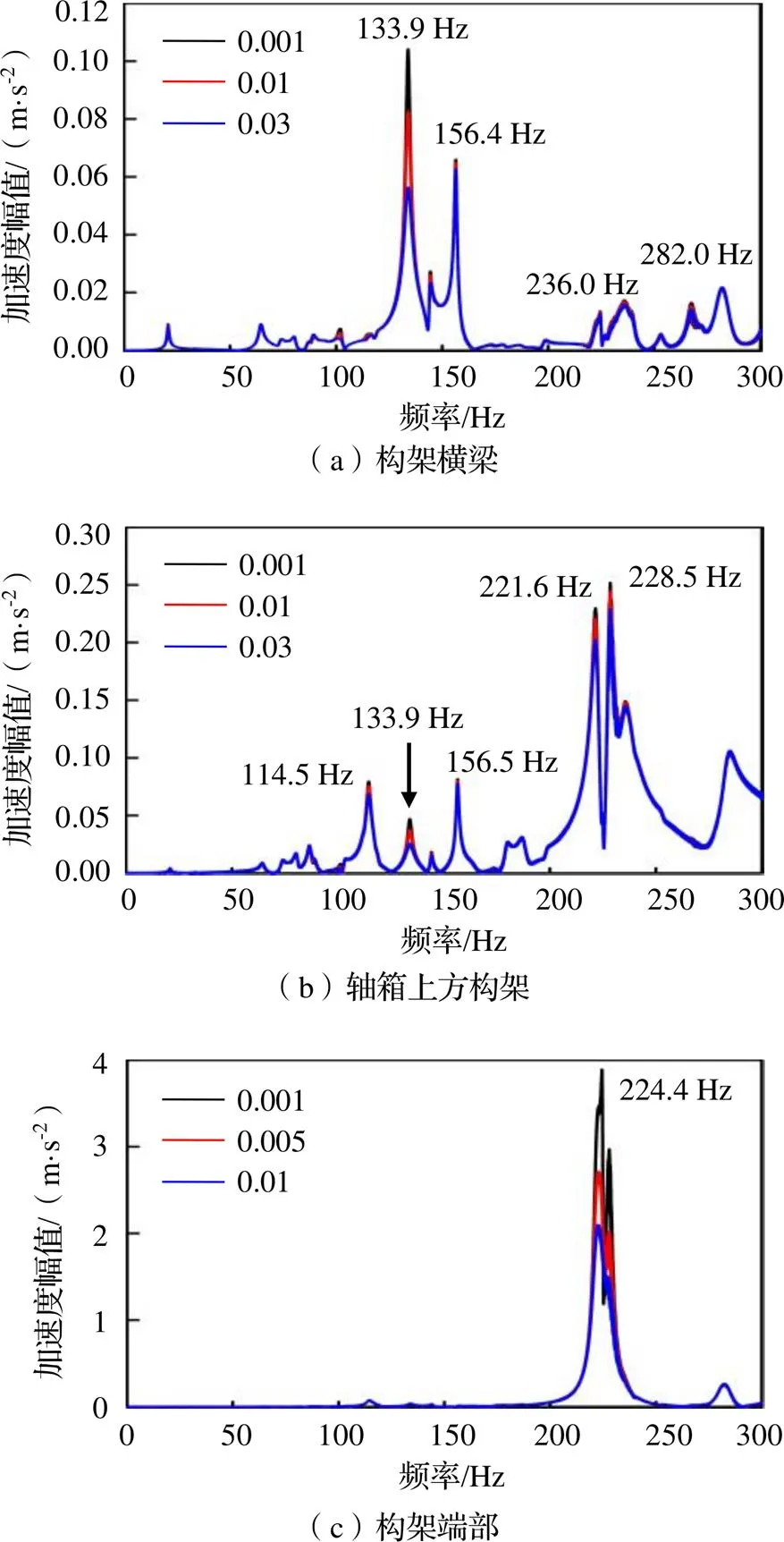
图6 浮沉工况下不同结构阻尼比的构架关键部位加速度频域图
侧滚扫频激励下三个关键位置的加速度频域图如图7所示。
可知,侧滚工况下,转向架构架主要表现主频为111.7 Hz等模态。其中,167.5 Hz为构架侧梁同向二阶垂弯模态;198.2 Hz为构架侧梁反向二阶垂弯模态;221.5 Hz、224.7 Hz、228.0 Hz和240.1 Hz为构架端部局部纵向摆动模态。结合不同轨道类型轮轨耦合振动频率和钢轨波磨通过频率可知:167.5 Hz模态容易在18 mm弹性短轨枕、普通短轨枕和12 mm弹性短轨枕线路上被轮轨高频激励激发;频率198.2 Hz、221.5 Hz、224.7 Hz、228.0 Hz和 240.1 Hz容易在减振型扣件、18 mm弹性短轨枕和12 mm弹性短轨枕线路上被轮轨高频激励激发。另外,构架端部加速度幅值明显大于构架横梁和轴箱上方构架,说明构架端部在实际服役情况下更容易发生模态结构共振。研究同时发现,110 Hz和220 Hz左右的模态响应受结构阻尼比影响较大,并且随着阻尼比的提高,构架振动响应呈衰减趋势。

图7 侧滚工况下不同结构阻尼比的构架关键部位加速度频域图
点头扫频激励下三个关键位置的加速度频域图如图8所示。
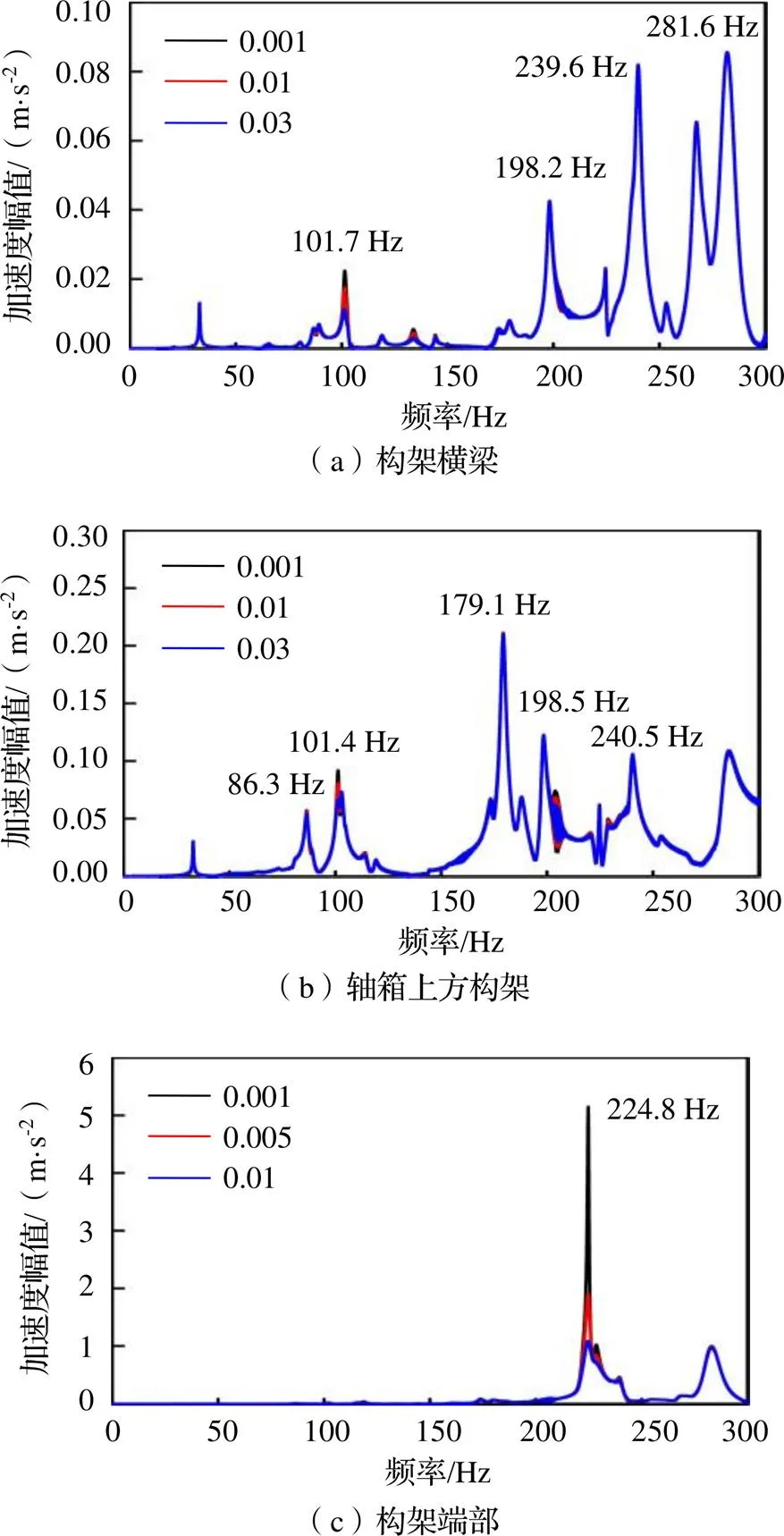
图8 点头工况下不同结构阻尼比的构架关键部位加速度频域图
可知,点头工况下,转向架构架主要表现主频为101.4 Hz等模态。其中,101.4 Hz为构架侧梁同向一阶垂弯和反向一阶横弯模态;198.2 Hz为构架侧梁反向二阶垂弯模态; 224.8 Hz和239.6 Hz为构架端部纵向摆动模态。分析可知,101.4 Hz模态容易在18 mm弹性短轨枕、普通短轨枕、12 mm弹性短轨枕以及单趾弹簧扣件线路上被轮轨高频激励激发;179.1 Hz模态与钢轨一阶弯曲轮轨耦合振动频率接近;198.2 Hz、224.8 Hz和239.6 Hz模态容易在减振型扣件、18 mm弹性短轨枕和12 mm弹性短轨枕线路上被轮轨高频激励激发。此外,
构架端部振动响应远大于构架横梁和轴箱上方构架,说明地铁车辆在实际服役过程中构架端部更容易发生模态结构共振。最后,224.8 Hz模态响应受结构阻尼比影响最大,101.4 Hz模态次之,其他模态响应受阻尼比影响较小。
扭转扫频激励下三个关键位置的加速度频域图如图9所示。

图9 扭转工况下不同结构阻尼比的构架关键部位加速度频域图
可知,扭转工况下,转向架构架主要表现主频为80.4 Hz等模态。其中,80.4 Hz为构架侧梁横向反向弯曲模态;88.8 Hz为构架菱形变形模态;225.4 Hz和240.1 Hz为构架端部局部纵向摆动模态。结合不同轨道类型轮轨耦合振动频率和钢轨波磨通过频率可知:80.4 Hz和88.8 Hz模态容易在减振型扣件、18 mm弹性短轨枕、普通短轨枕、12 mm弹性短轨枕以及单趾弹簧扣件线路上被激发;225.4 Hz和240.1 Hz模态容易在减振型扣件、18 mm弹性短轨枕和12 mm弹性短轨枕线路上被激发。另外,构架端部加速度幅值最大,构架横梁加速度幅值最小,说明在实际服役条件下构架端部最容易发生振动疲劳破坏。研究同时表明,225.4 Hz模态响应受结构阻尼比影响较大,其他模态响应受结构阻尼比影响较小。
综上,各种服役模式下转向架构架224 Hz左右的构架端部局部模态容易被轮轨高频激励激发,特别是在弹性短轨枕和减振扣件区段与典型钢轨波磨激励频率较为接近。因此,应该特别注意转向架构架端部在这些区间的共振疲劳问题。
4.2 一系悬挂参数对构架振动响应的影响
基于地铁车辆构架扫频模型模拟构架浮沉、侧滚、点头和扭转四种工况,进一步研究一系悬挂刚度对构架主体及构架端部振动响应的影响,如图10所示。四种工况下的构架主体和构架端部振动响应规律相似,由图10可知,当一系垂向刚度在合理范围内变化时,其对构架主体及构架端部振动响应影响较小,说明一系垂向刚度对构架高频模态振动传递影响较小。
5 结论
本文首先考虑不同轨道类型轮轨耦合振动频率和钢轨波磨通过频率,开展转向架构架模态静态匹配研究;然后建立了转向架构架刚柔耦合动力学模型,并基于扫频法开展了构架模态动态匹配研究。得到以下结论:
(1)通过构架模态静态匹配研究发现,不同轨道类型轮轨耦合振动频率和钢轨波磨通过频率在37~41 Hz时,容易与构架扭转模态发生共振;频率在54~167 Hz时,容易与构架侧梁横向弯曲模态、构架侧梁垂向弯曲模态以及构架侧梁端部摆动模态发生共振;轮轨耦合振动频率在167~265 Hz时,容易与转向架构架侧梁端部摆动模态、构架端部纵向摆动模态以及构架侧梁和端部耦合模态发生共振。
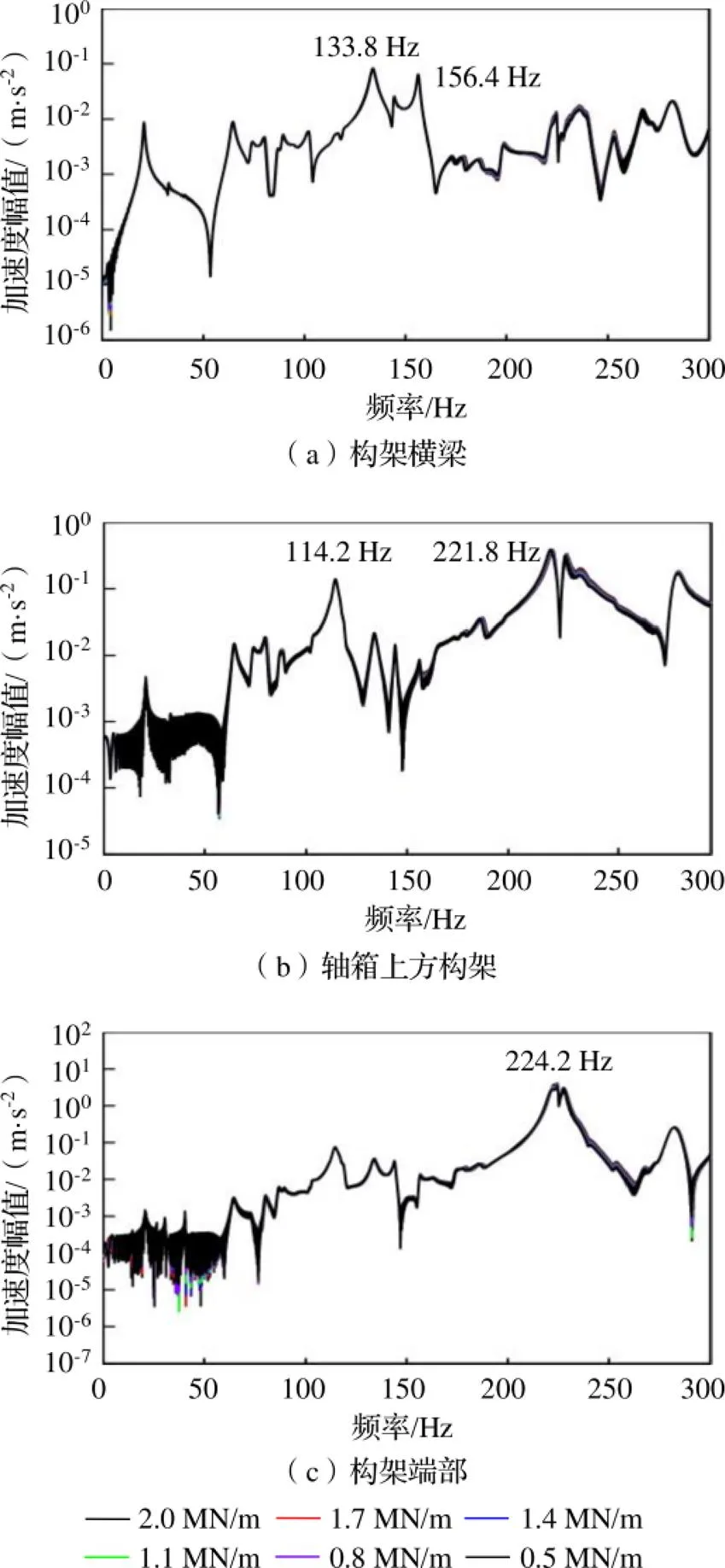
图10 浮沉工况下不同一系悬挂刚度的构架关键部位加速度频域图
(2)通过典型服役模式下构架模态动态匹配研究,识别了转向架构架敏感的工作模态;进一步结合不同轨道类型轮轨耦合振动频率和钢轨波磨通过频率分析了哪些工作模态在实际服役过程中更容易被轮轨高频激励激发,引起结构共振。结果表明,构架端部224 Hz的端部局部模态容易被弹性短轨枕和减振扣件典型钢轨波磨激励激发。
(3)研究了阻尼比和一系垂向刚度对构架振动传递的影响。发现一系垂向刚度在合理范围内变化时,对构架振动传递影响较小。阻尼比的提高对构架振动传递有一定衰减作用,其中对构架端部振动传递影响最大。
[1]张富兵,邬平波,屈升. 地铁车辆轮对安全吊的振动疲劳特性研究[J]. 机械强度,2018,40(4):810-814.
[2]董磊,王怀东,陈卓,等. 城市轨道车辆转向架构架振动疲劳失效影响因素分析[J]. 大连交通大学学报,2018,39(6):5-9.
[3]韩博. 地铁车辆转向架天线梁疲劳强度研究[D]. 北京:北京交通大学,2020.
[4]连青林,刘志明,王文静. 提速客车转向架安全吊座疲劳失效机理与改进方法[J]. 交通运输工程学报,2018,18(1):71-78.
[5]瞿绍奇,孙英超,邬亨贵,等. 飞行器径向连接螺栓振动断裂分析[J]. 航空学报,2021,42(5):358-363.
[6]石怀龙,王建斌,戴焕云,等. 地铁车辆轴箱吊耳断裂机理和试验研究[J]. 机械工程学报,2019,55(6):122-128.
[7]乐柄伸,吴兴文,黄运华. 高速列车车体动态薄弱位置及特征应力谱研究[J]. 机械,2020,47(9):9-16.
[8]翟婉明. 车辆-轨道耦合动力学[M]. 4版. 北京:科学出版社,2015.
[9]Wu X,Rakheja S,Cai W,Chi M. Ahmed AKW,Qu S. A study of formation of high order wheel polygonalization[J]. Wear,2019(424):1-14.
[10]李伟. 地铁钢轨波磨成因及其对车辆/轨道行为的影响[D]. 成都:西南交通大学,2015.
[11]李霞,李伟,温泽峰,等. 普通短轨枕轨道结构钢轨波磨初步研究[J]. 机械工程学报,2013,49(2):109-115.
[12]李霞. 地铁钢轨波磨形成机理研究[D]. 成都:西南交通大学,2012.
[13]王欣. 城市轨道交通减振降噪技术的应用[J]. 地铁与轻轨,2003(1):35-39,60.
[14]周磊. 地铁普通短轨枕整体道床P2力共振与一系钢弹簧寿命关系的研究[D]. 成都:西南交通大学,2019.
[15]马维国. 地铁车辆轨道系统P2共振特性研究[D]. 成都:西南交通大学,2019.
[16]刘晓丹. 高速铁路有砟轨道结构固有振动特性及轮轨耦合振动特性研究[D]. 北京:中国铁道科学研究院,2020.
[17]李飞. 基于动力学的地铁转向架构架振动疲劳研究[D]. 成都:西南交通大学,2021.
Investigation on the Modal Matching Method for a Metro Bogie
DONG Xiaohua1,WU Xingwen2,ZHAO Minghua3,LIANG Shulin1,LI Fei1
( 1.State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu610031, China; 2.School of Mechanical Engineering, Southwest Jiaotong University, Chengdu610031, China; 3.National Innovation Center of High Speed Train, Qingdao 266000, China )
Firstly, this paper investigates the wheel rail coupling vibration characteristics of different track types of subway lines and the distribution of rail wave wear wavelength with different curve radius and track types, and further studies the modal static matching of vehicle track system with the reference of the inherent modal information of the frame. Then, based on the rigid flexible coupling theory and modal synthesis method, the rigid flexible coupling dynamic model of metro vehicle considering frame flexibility is established. The modal dynamic matching of vehicle track system is studied through the frequency sweep method. Finally, the effects of the structure damping ratio of the frame and the primary suspension vertical stiffness of the bogie on frame vibration transmission are analyzed. On the basis of the above research, a set of modal matching method suitable for metro bogie is proposed to further identify the possible resonance section and sensitive working modes of the bogie frame.
modal analysis;rigid flexible coupling dynamic model;modal static matching;modal dynamic matching;structural damping ratio
U270
A
10.3969/j.issn.1006-0316.2022.07.004
1006-0316 (2022) 07-0020-09
2022-01-06
中国国家铁路集团有限公司科技研究开发计划(P2019J002);科技部重点研发计划(2018YFE0201401-01);四川省应用基础研究(2020YJ0075)
董晓华(1996-),男,甘肃民乐人,硕士研究生,主要研究方向为振动疲劳,Email:1013262346@qq.com。*通讯作者:吴兴文(1988-),男,四川成都人,博士,副教授,主要研究方向为振动疲劳,Email:xingwen_wu@163.com。
