基于T-S模糊故障树的转向架多态可靠性研究

刘雅萍，卢兴旺，戴鑫亮

基于T-S模糊故障树的转向架多态可靠性研究

刘雅萍1，卢兴旺2，戴鑫亮*,3

（1.中车青岛四方机车车辆股份有限公司技术中心，山东 青岛 266111；2.中车株洲电力机车有限公司，湖南 株洲 412001；3.西南交通大学牵引动力国家重点实验室，四川 成都 610031）

转向架是车辆系统的重要组成部件之一，由于其结构复杂，很难获得各个零部件完备的失效数据，这给转向架系统可靠性的研究带来了较大的困难。为了解决这一问题，本文采用建立T-S模糊故障树的方法对转向架系统进行可靠性建模。在引入专家库系统的情况下，邀请从事相关研究的具有不同工作背景的专家对各个故障的严重程度给出自然语言描述，利用模糊理论将专家对T-S模糊门规则的自然语言描述转化为模糊概率。同时构建转向架系统模糊故障树，并将其转换为贝叶斯网络进行分析计算，获得转向架在不同状态下各个零部件的关键重要度。计算结果表明，在转向架系统处于不同状态时，系统内各部件的重要度也有所不同。

转向架；可靠性；模糊理论；T-S模糊故障树；贝叶斯网络

铁路运输是现代交通运输系统中的重要组成部分，而高速铁路凭借快速、安全、便捷的特点进一步提高了铁路运输的影响力。自2004年来我国大力发展高速铁路，现阶段我国的高铁总运营里程已达到3.79万公里，如何保证这一庞大系统安全、平稳地运行成为近年来高铁建设的重点关注问题之一。转向架作为车辆系统的重要组成部件之一，其可靠性对车辆系统的总体可靠性有着重大影响。由于转向架的组成较为复杂，各个零部件均存在多种失效形式，且不同部件之间存在级联效应，这些特性给转向架系统的可靠性建模带来一定的困难。

目前国内外学者针对转向架系统可靠性建模开展了许多研究。王社锋[1]采用指数分布对客车转向架可靠性进行建模，并通过相对失效率及重要度，提出了转向架可靠度分配以实现转向架可靠性设计。LinShuai等[2]利用复杂网络可靠性理论分析转向架系统可靠性，并利用网络的拓扑学特性引入网络集聚测度对可靠性进行描述。LiWantong等[3]通过模糊综合评估及层次分析法建立转向架系统可靠性模型，研究转向架系统可靠性的分配问题，其结果大致与实际情况相符。Yin Huaixian等[4]利用城轨列车现场数据，采用生存分析理论中的极大似然估计对城轨列车转向架的失效概率进行计算，得到较为合理的计算结果。Zhu Lei等[5]对城轨车辆建立模糊故障树模型，用以分析底事件失效时转向架系统失效的概率，结果表明空气弹簧断裂、制动失效、踏面剥落和转向架轮缘磨损对转向架的性能有较大影响。王壮[6]通过动力学仿真及数据调研对转向架重要部件进行失效模式与影响分析。ZhengShuting等[7]建立贝叶斯网络模型对CRH2型车不同故障的因果关系进行分析。KouLinlin等[8]通过网络流模型分析CRH3型车的多态可靠性，结果表明，网络流模型在指导车辆日常系统运行和预测性维护方面具有良好表现。卢兴旺[9]建立转向架系统可靠性模型，给出通过T-S（Takagi and Sugeno）多态故障树计算转向架系统可靠性的方法，并以轮对为例分析其基本事件的重要度。操琴[10]通过对小样本失效数据的研究，采用E-Bayes及Bootstrap方法建立极少失效数据下货车转向架的可靠性模型。刘伟等[11]根据动车组运营数据统计在不同运营里程下转向架发生故障的频次，得出其失效概率符合威布尔分布的结论，并对分布参数进行了估计。

由上述研究成果可知，现阶段对于可靠性的定量研究主要基于失效数据，但转向架是一个复杂系统，如果要获得其中每一个部件完备的失效数据势必要耗费大量资源。为解决以上问题，本文引入专家库系统，根据专家对于某个特定时间段转向架处于某种状态的自然语言描述，结合模糊理论将其转化为模糊概率，再通过T-S多态故障树及贝叶斯网络模型对转向架的系统可靠性进行评估，从而降低转向架系统可靠性的建模难度。

1 转向架T-S多态故障树模型

为估计转向架系统可靠性，首先建立转向架T-S多态故障树模型。

1.1 转向架T-S故障树构建

T-S门是T-S多态故障树的重要组成部分，它由一系列的if-then规则组成，假设＝(1,2, …,X)为底事件，为顶事件，对于任意X（X∈）、分别存在X(a＝1, 2, 3, …,k)、(b＝1, 2, 3, …,)种故障状态。

T-S门规则如下：

如果底事件X的故障状态为X，则顶事件的故障状态为的可能性为：

式中：()表示某一事件的概率。

如果令规则总数为，则：

转向架系统的T-S故障树如图1、图2所示。该故障树包含22个底事件和11个中间事件，各个符号所代表的事件如表1所示。为顶事件，表示转向架失效。

1.2 故障状态分类

依据已有研究成果[9]，转向架主要零部件可按其服役状态划分为三种状态，如表2所示。

图1 转向架系统T-S故障树

图2 转向架系统T-S故障子树

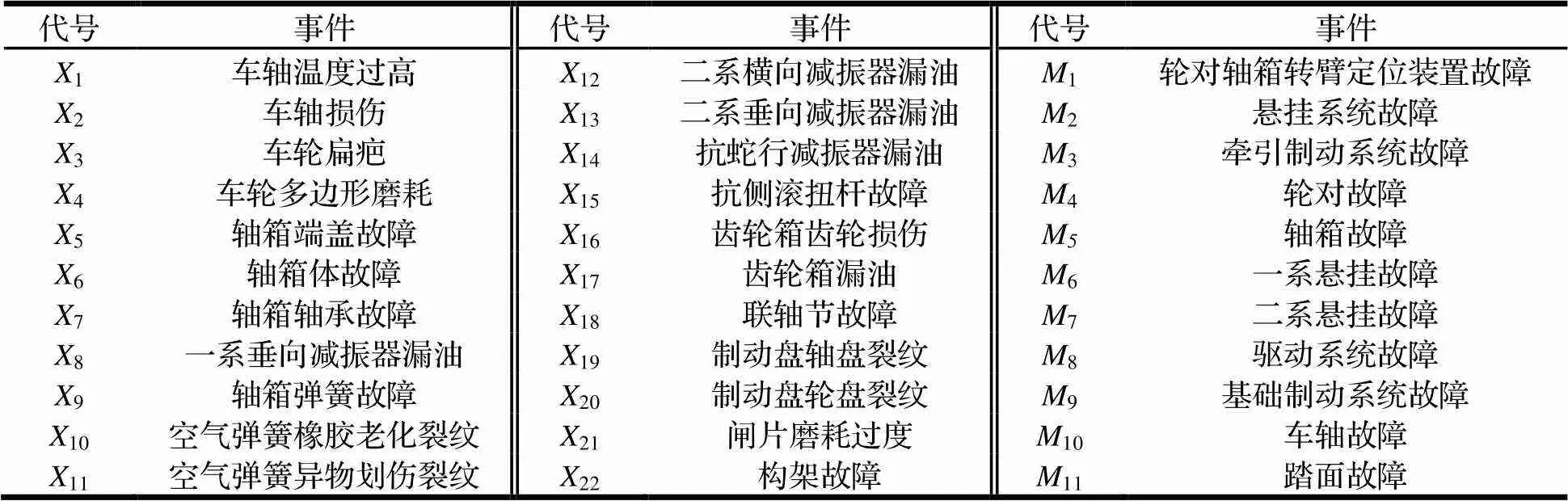
表1 事件代号及说明

注：1～22为底事件；1～11为中间事件。

以8一系减振器漏油为例，状态0表示减振器无泄漏；状态0.5表示减振器泄露致使减振器阻尼下降至初始值的50%～100%；1表示减振器泄露致使减振器阻尼下降至初始值的0%～50%。其余事件的故障程度也各自依照三态故障类别进行划分。

表2 状态分类及说明

2 T-S模糊故障树计算

计算T-S模糊故障需获得不同T-S门的计算规则，本文采用专家评分的方法将专家对故障发生概率的自然语言描述转化为模糊失效概率，再将故障树转化为贝叶斯网络进行转向架系统可靠性的计算。

2.1 专家选择及权重确定

通过专家库系统选取10名具有相关经验的专家，如表3所示，给出底事件及不同T-S门中输出事件所处状态可能性的自然语言描述。由于所选专家的职称、学历、工龄有所不同，因此采用层次分析法[12]确定不同专家的权重，如图3所示。

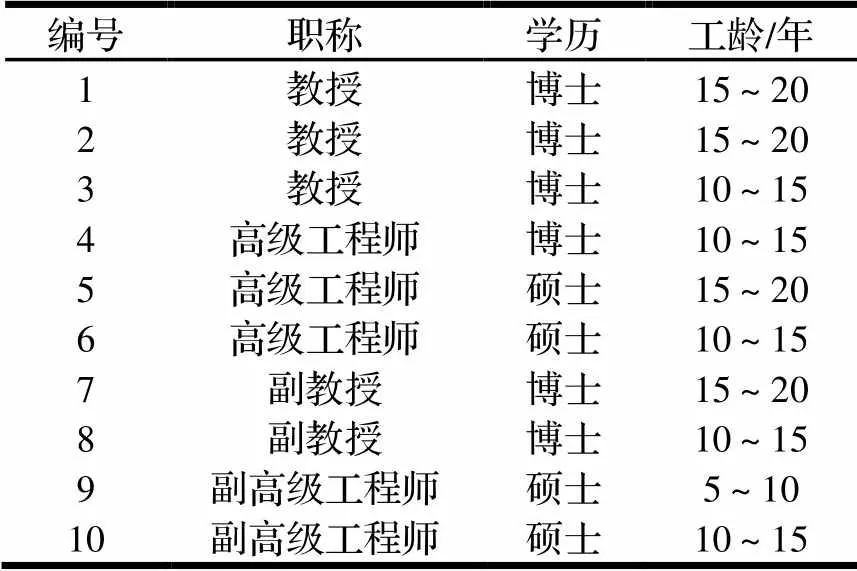
表3 专家情况

图3 层次结构

使用层次分析法时，需要构造判断矩阵，因此，从专家库中额外选取一名专家根据其情况制定判断矩阵，为：

通过该判断矩阵计算表3所列专家的权重向量，为：＝[0.14, 0.14, 0.13, 0.13, 0.11, 0.1, 0.09, 0.07, 0.04, 0.05]T。

2.2 模糊数与模糊失效概率的转换

专家首先通过自然语言给出各个失效事件中，每种状态发生概率的大小，再根据图4所示的转换规则，将自然语言转化为模糊数。自然语言对失效概率的描述为：很小（1）、小（2）、较小（3）、中等（4）、较大（5）、大（6）、很大（7）。各模糊数对应的隶属度如式（4）～（7）所示。

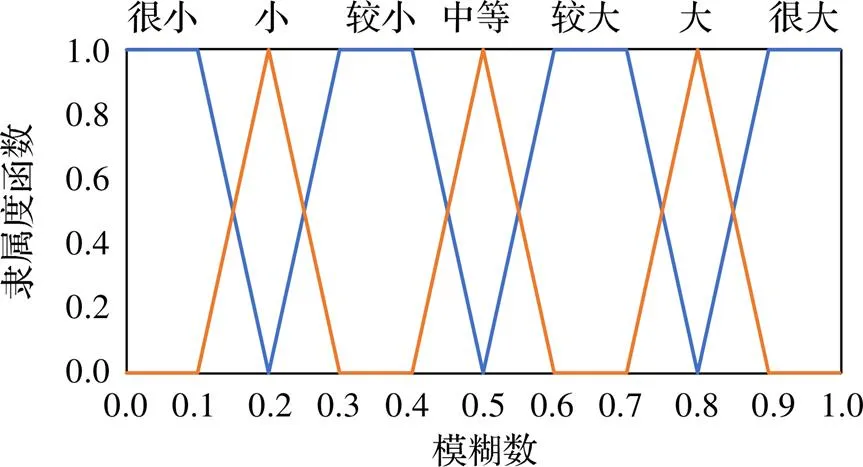
图4 模糊数与自然语言描述关系

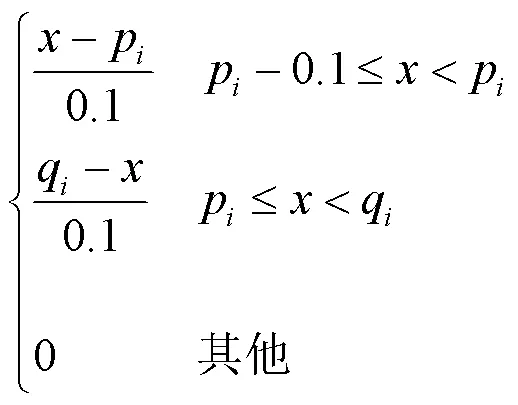
式中：为模糊数；p、p、q、q系数如表4所示。

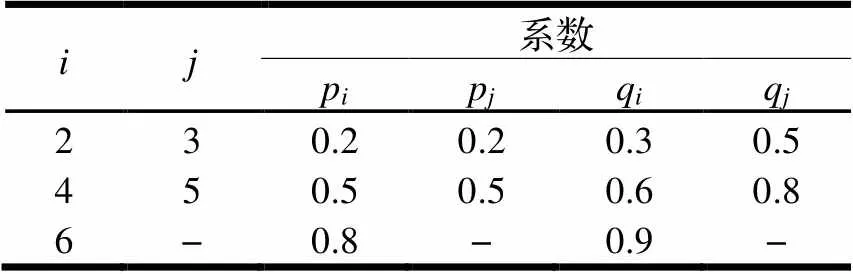
表4 隶属度函数系数表

下面以一系减振器漏油为例说明如何将模糊数转换为模糊概率。

＝max|1·g()2·g()…w·g()|（8）

将自然语言描述向量代入式（8），得到加权后模糊数的函数关系为：

最终计算出减振器漏油故障处于半故障状态的模糊失效概率为8×10-3，采用同样的方法得到减振器处于完全故障和无故障的模糊失效概率为6.915×10-4、1.237×10-4。此时需要注意，由模糊数转换而来零部件处于各个状态的模糊失效概率之和不为一，因此需将其进行归一化得到最终的概率。通过上述方法可到T-S模糊故障树中各个模糊门的规则，由于数据较多，这里仅列出T-S门12的数据，如表5所示。

表5 T-S模糊门12的规则

2.3 贝叶斯网络构建

构建好的T-S模糊故障树与贝叶斯网络相对应，其中T-S的基本事件、中间事件与顶事件分别对应贝叶斯网络中的根节点、中间节点和叶节点[15]，由此构建贝叶斯网络如图5所示。

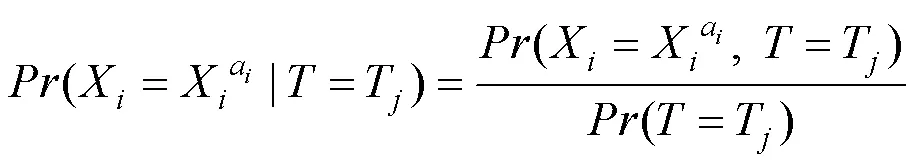
图5 转向架系统贝叶斯网络

3 转向架系统可靠性分析

通过图5及式（11）、式（12）所示关系可以计算出在底事件处于状态集中任一状态时，系统的可靠度以及各个部件的重要度。

3.1 已知底事件状态时顶事件所处状态计算

当已知部分底事件状态时，可计算求得顶事件所处状态的单边概率，由于每个事件状态均为离散值，状态集中元素较多，本文仅列出几种工况下顶事件的单边失效概率，如表6所示，选取的底事件为失效概率较高的部件。由表6可知，当3、4处于1状态时，顶事件有极大概率处于1状态。

表6 部分状态下顶事件失效概率

3.2 重要度计算

计算编号为1～22各部件关键重要度，如图6所示。

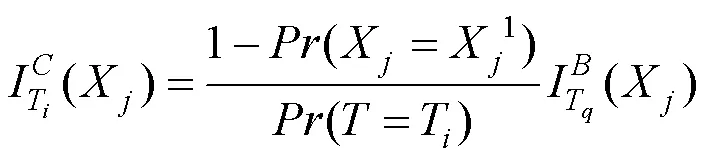
（14）

可知，在顶事件处于不同状态时，各个部件的重要度会有所不同。当转向架处于1状态时与空气弹簧相关的部件具有很高的重要度，同时与车轮踏面相关的故障由于发生概率较大，且容易对其他部件造成级联效应，其重要度也较高。

4 结论

本文通过引入专家库系统、构建T-S模糊故障，对转向架系统可靠性进行了分析，解决了故障数据匮乏的问题，同时能够较好地找到不同部件之间发生失效的关联。此外，借助贝叶斯网络实现了对顶事件失效概率的正向推导，以及根据顶事件状态逆向推导部件重要度的功能。通过计算不同部件的重要度可以发现，空簧与轮对相对于其他部件具有更高的重要度，该结果为转向架日常维护及检修工作提供了一定参考。

[1]王社锋. 客车转向架系统可靠性设计研究[J]. 铁道车辆，2007，45（6）：1-3.

[2]Lin S，Jia L，Wang Y，et al. Reliability Study of Bogie System of High-Speeda Train Based on Complex Networks Theory[C]. Proceedings of the International Conference on Electrical and Information Technologies for Rail Tr nsportation - Electrical Traction，2016.

[3]Li W，Qin Y，Lin S，et al. Reliability Allocation of High-Speed Train Bogie System[C]. Proceedings of the International Conference on Electrical and Information Technologies for Rail Transportation - Electrical Traction，2016.

[4]Yin H，Wang K，Qin Y，et al. Analysis of Urban Rail Vehicle Bogie System Reliability Based on the Theory of Survival[C]. Proceedings of the International Conference on Electrical and Information Technologies for Rail Transportation - Electrical Traction，2016

[5]Zhu L，Zhang Z，Qin Y，et al. Reliability Analysis of Metro Vehicles Bogie System Based on Fuzzy Fault Tree[C]. Proceedings of the International Conference on Electrical and Information Technologies for Rail Transportation - Electrical Traction，2016.

[6]王壮. 动车组转向架服役可靠性和维修性研究[D]. 成都：西南交通大学，2015.

[7]Zheng S，Qin Y，Wang L，et al. Bayesian Network-Based Reliability Analysis of High-Speed Train Bogie System[C]. Proceedings of the 3rd International Conference on Electrical Engineering and Information Technologies for Rail Transportation （EITRT），2018.

[8]Kou L，Qin Y，Jia L，et al. Multistate Reliability Evaluation of Bogie on High Speed Railway Vehicle Based on the Network Flow Theory[J]. International Journal of Software Engineering and Knowledge Engineering，2018，28（4）：431-451.

[9]卢兴旺. 转向架系统可靠性模型和T-S多态故障树分析[D]. 成都：西南交通大学，2020.

[10]操琴. 极少失效数据下的铁路货车转向架大部件可靠性评估与检修策略优化[D]. 北京：北京交通大学，2020.

[11]刘伟，张冬梅，高磊. 基于运营数据的某型动车组转向架可靠性分析[J]. 铁道车辆，2021，59（4）：31-34.

[12]Mironova N，Hafizova K，Ieee. Analytic Hierarchy Process based on fuzzy logic[C]. Proceedings of the 9th International Conference on the Experience of Designing and Application of CAD Systems in Microelectronics，Lviv，UKRAINE，F Feb 19-24，2007.

[13]夏冉. 基于模糊故障树方法的脐带缆可靠性分析研究[J]. 海洋工程，2021，39（2）：153-161.

[14]Chen S-J，Hwang C-L. Fuzzy multiple attribute decision making methods[M]. Fuzzy multiple attribute decision making，1992：289-486.

[15]李鹏. 基于BN和T-S模糊故障树的起重机变幅机构可靠性评估[J]. 中国工程机械学报，2021，19（3）：273-277.

[16]Birolini A. Reliability engineering[M]. Springer，2017.

Multi-State Reliability Study of BogiesBased on T-S Fuzzy Fault Tree

LIU Yaping1，LU Xingwang2，DAI Xinliang3

( 1.R&D Center, CRRC Qingdao Sifang Co., Ltd., Qingdao 266111, China; 2.CRRC Zhuzhou Locomotive Co., Ltd., Zhuzhou 412001, China; 3.State key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu 610031, China )

Bogie is one of the important components of the vehicle system. Due to its complex structure, it is difficult to obtain complete failure data of each component, which brings great difficulties to the study of the reliability of this bogie system. To solve this problem, in this paper, the reliability modelling of the bogie system is carried out using T-S fuzzy fault trees. With the introduction of an expert database system, experts with different working backgrounds engaged in related research are invited to give natural language descriptions of the severity of each fault, and the natural language descriptions of the T-S fuzzy gate rules by experts are transformed into fuzzy probabilities using fuzzy theory. The fuzzy fault tree of the bogie system is also constructed and converted into a Bayesian network for analysis and calculation to obtain the importance of each component of the bogie in different states. The results show that the importance of each component in the system varies when the bogie system is in different states.

bogie；reliability；fuzzy theory；T-S fuzzy fault tree；Bayesian network

U268.3

A

10.3969/j.issn.1006-0316.2022.07.005

1006-0316 (2022) 07-0029-07

2021-12-21

刘雅萍（1978－），女，甘肃武威人，高级工程师，主要研究方向为轨道车辆工程，E-mail：liuyaping@cqsf.com。*通讯作者：戴鑫亮（1992－），男，新疆乌鲁木齐人，博士研究生，主要研究方向为机车车辆可靠性、维修性、数据分析等，E-mail：dxl@my.swjtu.edu.cn。