面向图计算内存系统的实现与拓展
2022-08-01刘令斌黄建强黄东强
刘令斌,任 龙,黄建强,黄东强
(青海大学计算机技术与应用系,青海 西宁 810016)
随着信息技术的高速发展,人类迎来了大数据时代,导致数据规模急剧增长。近几年,Twitter的月活跃用户产生的数据占几百GB甚至TB级别的存储量[1],现实生活所产生的规模庞大的各种类型的数据,基本都可以抽象为图数据结构(graph-structured data)[2-3]。然而,传统的图计算算法处理大规模图数据具有很明显的缺陷,因此,如何高效处理大规模图数据成为很多研究的重点问题。Ligra是解决此类问题性能最好的图计算系统之一[4]。Beamer等[5]提出了关于遍历方式的优化,Ligra使用这种优化方式,以 广度优先搜索算法(Breadth First Search,BFS)为例,不同于传统的 BFS 算法中由源点到底端的遍历方式,Ligra 通过阈值判断需要遍历的点集是否稀疏——如果稀疏则使用 Top-Down 自上而下的方法进行遍历;如果稠密,则使用 Bottom-Up 自下而上的方法进行遍历,从而解决负载不均衡的问题[6-7],能高效地使用多线程并行。同时,在大规模图计算领域中,国内外学者通过研究找到了新的优化方向[8-12]。Ligra实现了 BFS、单源最短路径(Single-Source Shortest Path,SSSP)等图计算算法的优化 ,但是支持的图计算算法仍不全面,存在可拓展的空间。
本文通过对 Ligra 进行拓展,实现深度优先搜索算法(Depth First Search,DFS)及子图匹配算法,用来更好地解决传统图计算算法运算速度过慢的问题。
1 图计算系统的实现
1.1 存储格式
表1中以图数据soc-Livejournal为例,展示不同格式下数据大小及获取点的出度所需要的时间。其中,ELL(ELLPACK)格式与邻接矩阵格式需要占用超过50 GB的存储空间;如果使用COO(Coordinate)格式进行存储,仅需要0.9 GB的存储空间;使用CSR(Compressed Sparse Row)格式存储需要0.5 GB的存储空间。由此可见,CSR格式与COO格式在存储图数据方面具有比较明显的优势。在获取出度信息时,CSR格式需要的处理时间较少,由此可见, CSR格式的图数据适用于大规模图计算算法,故选取CSR格式来存储图数据。

表1 存储数据大小及处理时间Tab.1 Storage capacity and processing time
1.2 接口的实现
1.2.1 EDGEMAP 接口 EDGEMAP接口具有要处理的图数据G、要遍历的顶点集合U、1个功能函数F及判断某点是否被标记的函数P等4个参数。以BFS 算法为例,该算法的遍历过程是按层进行的,在每一层遍历的时候,需要遍历的点是对上一层进行处理后得到的未访问过的点,也就是集合U,对某点是否被访问过的判断是通过函数P实现的,判断访问标记是否需要修改及修改访问的标记是通过功能函数 F实现的,需要遍历的边存储在图数据G中。同样的,在Bellman-Ford算法中,U表示当前层需要遍历的点集,G表示需要处理的图数据,函数P用于判断某点是否被访问过,而函数F的功能发生了变化。不同于BFS算法中判断某点的标记是否需要被修改与更改访问标记的功能,在Bellman-Ford算法中,函数F需要实现的功能是判断某边的出发顶点距离源点的最短距离与该边的权值之和是否小于该边的目标顶点距离源点的最短距离,并且更改某点与源点之间的最短距离。
EDGEMAP接口的伪代码如下所示。具体解释为根据点集U的密集程度来判断应该使用自上而下的方式还是自下而上的方式进行遍历,如果点集U中的点数与各点的出度之和大于图数据的边数/20,则使用自下而上的遍历方式,反之,则使用自上而下的遍历方式。

Algorithm 1 EDGEMAP1:procedure EDGEMAP(G(V,E),U,F,P)2:if (|U| + sum of out - degrees of U>|E|/20) then3: return EDGEMAPDENSE(G(V,E),U,F,P)4:else5: return EDGEMAPSPARSE(G(V,E),U,F,P)6:end if
1.2.2 EDGEMAPDENSE接口 EDGEMAPDENSE接口的伪代码如下所示。接口包含要处理的图数据G、要遍历的顶点集合U、1个功能函数F及判断某点是否被访问的函数P等4个参数。EDGEMAPDENSE接口实现了自下而上遍历的功能。具体思路为遍历图数据G中所有的点的集合V,每当遇到未被访问过的点时,就遍历该点的所有入度点,通过函数P来判断如果在该点的所有入度点中存在被访问过的点,则通过函数F修改该点的标记,并将该点记录到下一层需要访问的点集中,之后继续通过函数P来寻找下一个未被访问过的点,直到遍历完V中全部的点。

Algorithm 2 EDGEMAPDENSE1:procedure EDGEMAPDENSE(G(V,E),U,F,P)2:New={}3:fori ∈ {0,|V| - 1} do4: ifP(i) == -1 then5: forn ∈ getlnDegree(i) do6: ifP(n)! = -1 & F(n,i) == 1 then7: New ←New U {i}8: end if9: ifP(i)! = -1 then10: break11: end if12: end for13: end if 14:end for 15:returnNew
1.2.3 EDGEMAPSPARSE 接口 EDGEMAPSPARSE接口的伪代码如下所示。接口具有要处理的图数据G、要遍历的顶点集合U、1个功能函数F及判断某点是否被访问的函数P等4个参数。EDGEMAPSPARSE接口实现了自上而下遍历的功能。具体思路为遍历点集U中所有点的出度点,通过函数P来进行判断,每当遇到未被访问过的点时,则通过函数F来判断该点是否符合修改访问标记的要求,如果符合要求,则修改该点的标记,并将该点记录到下一层需要访问的点集中,反之,则不进行修改与记录,继续遍历,直到遍历完点集U中全部点的出度点。

Algorithm 3 EDGEMAPSPARSE1:procedure EDGEMAPSPARSE(G(V,E),U,F,P)2:New={}3:forv ∈ U do4: forn ∈ getOutDegree(v) do5: ifP(n) == -1 & F(v,n) == 1 then6: New ← New U {n}7: end if8: end for9:end for10:returnNew
1.3 解决负载不均衡问题的方法
在图计算算法运算时,由于图分布的幂律特性[13],在逐层遍历的过程中,需要遍历的点集规模会出现先是几十倍地增长,然后几十倍地减少现象。这是由于点集中存在少量的顶点出度远远大于其他顶点,在运算过程中,这些顶点的存在会给处理该点的线程带来远超于其他线程的任务量,从而造成严重的负载不均衡的问题,在很大程度上降低了图计算算法的并行效率。
为了解决负载不均衡问题,本研究采用Top-Down与Bottom-Up相结合的遍历方式。Top-Down从当前层需要遍历的点集出发,依次访问它们的出度点,并将没有访问过的出度点加入到新的点集中。Bottom-Up扫描所有没有访问过的点,依次遍历这些点的父节点,如果存在某个父节点被访问过,则将该点加入到新的点集中。Bottom-Up的优势在于具有“提前跳出循环”的判断,即只要某点有一个父节点被访问过,剩余的父节点就不需要再进行遍历,在最优的情况下,只需要访问一个父节点就可以将该点加入到新的点集中,而算法的复杂度由O(|E|)降为O(|V|)。而Top-Down不具有这种优势,必须要全部遍历点所有的出度点。
一般而言,根据图分布的幂律特性,在遍历前几层的过程中,由于点集中的点相对较少,Top-Down仅需遍历当前点集中的出度点,相对而言具有较高的效率。而到了中间几层,点集中会出现出度较大的点,Bottom-Up对每一个没有访问过的点,只需遍历其部分父节点,便可以判断是否加入到新的点集中,避免出现有的线程任务量过多的情况,解决了负载不均衡的问题,因而会具有较高的效率。在处理最后几层时,剩下的大多是度数较小的点,可以使用Top-Down进行遍历。
1.4 减少互斥锁的使用
在并行计算的过程中,会出现多个线程同时访问并修改某一共享内存中的数据的情况。以BFS过程为例,当线程1访问s0点时,发现该点没有被访问过,就会将该点加入到新的点集中,并修改s0点的标记,但在线程1修改s0点的标记之前,线程2可能也正在访问s0点,那么线程2就会将s0点重复加入到新的点集中,于是在下一层遍历时就会产生不必要的任务,增加算法运行时间。为了避免这种情况的出现,会使用互斥锁或者原子操作来保证对某一变量的访问或修改只允许一个线程来进行,当一个线程操作结束后,才允许下一个线程进行相应的操作。
相比较于原子操作,互斥锁具有功能多样的优势,使用更加灵活,可以自主选择需要加锁的区域。但是,互斥锁的性能不及原子操作,需要运行的时间更久,而且可能会出现“死锁”的情况。所以为了减少系统中算法的运行时间,要尽可能地使用原子操作来代替互斥锁。一般情况下,原子操作可以实现的功能较为单一,所需要的功能要在原有的原子操作的基础上进行拓展。此处便实现了在原子操作CAS(compare-and-swap)的基础上,实现了比较并存储两者间较小值的原子功能,完成了优化。
原子操作的伪代码如下所示。接口具有地址L、旧值O、新值N等3个参数。如果L中存储的值等于O,则将L中的值更改为N,且返回true,否则返回false。而拓展的原子功能便是基于CAS操作实现的,命名为writeMin。writeMin具有地址L、新值N等2个参数,如果L中存储的值大于N,则将L中的值更改为N,且返回true,否则返回false。

Algorithm 4 writeMin1:procedure writeMin(*L,N) 2:O ← *L3:r ← false4:whileO>N & !(r = CAS (L,O,N)) do5: O ←*L6:end while7:return r
2 图计算系统的拓展
2.1 深度优先搜索算法
传统的DFS算法需要输入图数据G=(V,E)及源点s,定义一个队列来存储需要遍历的点,定义一个数组来标记访问过的点。首先,将所有点标记为未访问的状态,遍历s所能到达的所有顶点,并存入队列中,将s的标记改为已访问;然后取出队列末尾元素s1,如果s1未被访问过,则将s1所能到达的所有顶点存入队列中,并将s1的标记改为已访问。直到找到问题解或者队列为空,结束搜索。
与传统的遍历方式不同,对Ligra图计算系统拓展后实现的DFS算法,采用分块遍历的方法来尽可能地提高遍历效率。首先,将源点的出度点按照线程数分块,使得每一个线程处理的任务量尽可能相同,各线程并行进行搜索,从而提高运算效率;然后在遍历的过程中,对队列中的任务量进行判断,如果某个线程中的任务量超过阈值,则将该线程的任务进行平分,由两个线程来共同完成,直到各个线程的任务量小于或等于阈值。需要使用#pragmaomptask将任务加入到新的线程中,从而完成任务调度。通过分块遍历的方式来实现搜索,不仅较好地解决了负载不均衡的问题,而且能提高运算效率。
2.2 子图匹配算法
子图匹配算法是在深度优先搜索算法的基础上,对点的映射进行判断的图计算算法。该算法用于找出目标图中的点与子图中点的映射关系。算法需要输入子图g=(v,e)及目标图G=(V,E)。首先,获取子图中每一个点的特征,如入度、出度、关联点,以及该点是关联点的入度点还是出度点等信息;目标图中的每一个点也需要获取特征:入度、出度、入度点、出度点等信息。然后由目标图的0点开始,依次遍历,找到一个与子图0点相匹配的点。假设目标图中a点与0点相匹配,子图中1点作为0点的出度点,则遍历目标图中a点的所有出度点,找到一个与子图中1点相匹配的点。重复这个过程,直到子图中所有的点都找到匹配的点或者目标图遍历完毕,没有找到解。
对Ligra图计算系统进行拓展,实现了子图匹配算法。首先,对子图中每一个点的特征信息进行提取,之后对目标图中的点依次处理,直到找到第一个与子图0点相匹配的点;然后,找到子图中将0点作为关联点的1点。如果0点作为1点的出度点,则通过分块遍历的方式,使用多线程对目标图中与0点相匹配的点的出度点进行并行处理,并将相匹配的点加入到队列中,找到完全匹配的一组点后,令多余点出队列,继续匹配所有的可能性,直到达到处理目的或者完成目标图的遍历。
3 实验结果与性能分析
3.1 实验数据
实验所选取的测试数据均为真实的图数据。soc-livejournal[14]、twitter7[15]和high-twitter[16]是真实的社交网络,其中soc-livejournal包含484万个顶点和6 899万条有向边,twitter7包含4 165万个顶点和14.7亿条有向边,high-twitter包含45万个顶点和1 485万条有向边;uk-2002代表网页间的超链接,包含1 852万个顶点和2.98亿条有向边。图数据规模如表2所示,表格中记录了每一个数据集的点数(用|V|表示)、边数(用|E|表示)及数据大小。

表2 数据规模Tab.2 Data scales
3.2 性能对比
表3的数据是测试high-twitter图得到的结果(包括用传统的图计算算法和基于图计算系统实现的图算法处理图数据得到的结果)。其中,Serial行中的“—”表示1 800 s内仍未处理完毕,解决SSSP问题的Bellman_Ford算法的时间复杂度为O(V·E),几乎无法应用于处理大规模的图数据,子图匹配算法是在目标图中找到100 000 00组不重复的子图所需要的时间。性能加速比是以传统图计算算法的处理时间为基准,来除以图计算系统的处理时间得到的数值。由表3中性能加速比的数值可以看出,图计算系统的处理速度远高于传统的图计算算法。这是由于图计算系统能够更好地利用多核资源,并且通过自下而上与自上而下相结合的遍历方式,解决了并行过程中负载不均衡的问题,使得图计算系统的性能得以提高。

表3 high-twitter 处理时间Tab.3 Processing time of high-twitter
对于其他大规模图数据的处理结果如表4所示。在处理超过900 MB的图数据时,传统的图计算算法已经无法在1 800 s内完成计算。而基于图计算系统实现的图算法依然可以快速地处理大规模图数据,更好地满足人们的需求。
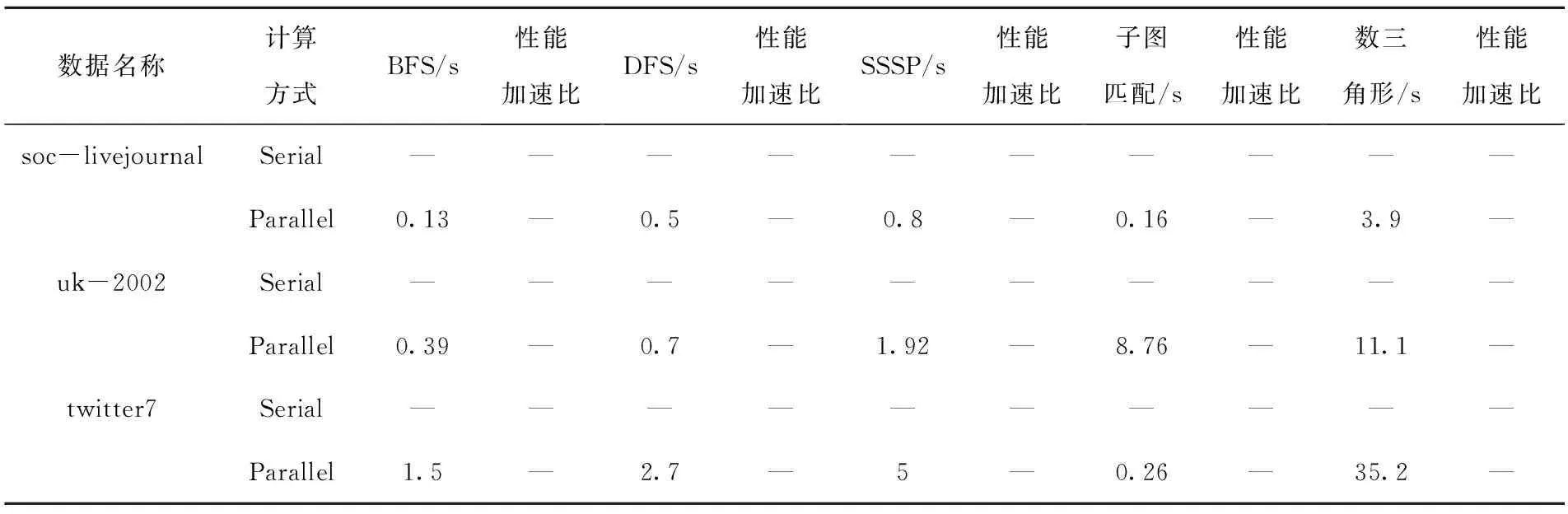
表4 其他数据集处理时间Tab.4 Processing time of other datasets
3.3 CPU利用率
表5为每一个程序在运行时CPU的有效利用率。因为传统的图计算算法都是串行算法,仅使用主线程来完成计算,所以CPU利用率很低。而基于图计算系统实现的图算法为并行算法,能充分地利用多线程资源来完成计算,并且通过合理的遍历方式减少了负载不均衡问题的影响,使得CPU利用率得到提升。

表5 CPU利用率Tab.5 CPU utilization %
图1为处理high-twitter图数据时的CPU利用率。从图1可以发现,基于图计算系统的图算法的CPU利用率仍然不是特别高,这是因为大部分的图计算算法具有不规则性:图中各个点的度数极度不规则,导致负载不规则,使得硬件效率低;图遍历依赖于图结构,导致遍历不规则,使得cache命中率较低;更新依赖于上一层遍历结果,导致更新不规则,使得图计算更加复杂。这是目前图算法问题中亟待解决的难题,也是未来努力的方向。

图1 high-twitter CPU 利用率Fig.1 CPU utilization of high-twitter
4 讨论与结论
本文从传统的图计算算法存在的劣势切入,通过优化图算法来高效地处理大规模图数据。与Shun等[4]实现的图算法不同,本文拓展了DFS 算法及子图匹配算法。在优化图计算的遍历方式时,与Beamer等[5]提出的自上而下与自下而上的混合方式不同,加入CSC格式来简化图数据的访问。同时,还拓展原子操作来代替互斥锁,使得并行计算的运算速度得到提升。算法中,图数据存储为CSR格式,无法将需要遍历的边数据全部存储到cache中,如果能进一步压缩图数据,使其可以存储到cache中,则可以提高算法性能。在以后的研究中,可以尝试使用位图或者分块等方法,对图数据的存储方式进行优化,从而进一步优化图算法。
