基于小波包能熵谱的爆震特征频带及强度分析

薛劲梓，胡春明，刘娜，赵英博，张建飞

(1.天津大学内燃机研究所，天津，300072；2.天津大学机械工程学院，天津，300350)

点燃式发动机的爆震燃烧属于不正常的燃烧现象，爆震会使燃烧室内的压力曲线在上止点附近呈现锯齿状，爆震程度越大，这种形状越发明显、振荡幅度也越大。为了监测发动机的运行状态，需要准确评估爆震强度。相较于缸体振动信号的检测方式，基于缸压的爆震检测指标是一种较为准确的判别方法。

爆震会激发燃烧室谐振，使缸压中的高频成分升高，所以，对于缸压信号，使用4～20 kHz 高通滤波器提取其中的高频分量，将滤波后高频振荡压力的最大幅值(the maximum amplitude pressure oscillation，MAPO)作为爆震强度的评价指标[1-2]，对爆震有一定的指示效果。但是，当缸压信号因外部电信号干扰出现毛刺、噪点时，提取出的MAPO 将会因为干扰存在而不可靠，导致错误的检测结果。为了克服这一缺点，Siemens VDO爆震算法将低通滤波后的最大压力点作为爆震始点，在爆震始点前后部分(参考窗口和爆震窗口)信号进行积分，取爆震窗口与参考窗口高频信号的积分之比作为爆震因子(knock factors，KF)[3-4]，若KF大于一定的阀值则认为是爆震循环。Siemens VDO算法虽然在一定程度上能消除信号出现毛刺的影响，但是其结果依赖于爆震始点、爆震窗口宽度等关键参数的人为主观设置。

近年来，小波包分析作为一种精细的时频分析工具应用在特征信号的提取上，其具有削弱干扰，突出信号特征的优点。史历程等[5]将小波变换和熵原理结合，利用小波分解计算出小波能量熵，得到在不同尺度内的能量分布情况，从而提取出传感器故障信号的特征。与小波分解相比，小波包变换能够提供更高的分辨率，能够对信号的低频和高频部分进行分解，从而得出多级小波包分解树的结构。杨兴国[6]利用小波包变换与双谱估计相结合的方法提取发动机声信号特征向量作为输入，通过机器学习中支持向量机的算法对模型训练来识别发动机的异响。刘成材等[7]在基于加速度传感器检测发动机爆震的研究中，对缸体振动信号进行了小波包分解并重构信号，从重构后的振动信号提取出爆震特征，尤其增强了发动机轻微爆震检测性能。

本文作者使用小波包变换的方法处理缸内燃烧压力的信号，提取其中高频压力分量，计算有效频带的范数能量熵并得到小波包能熵谱。然后，从分析大量爆震试验所获得的样本统计值出发，探究不同爆震强度样本下的小波包能熵谱分布情况。最后基于小波包能熵谱的分析提出一种新的爆震强度指标，验证其可行性和有效性，并利用ROC曲线估计出选定工况下的爆震阈值。

1 小波包变换分析方法

1.1 小波包分解基本原理

在小波变换的基础上，小波包变换可以进一步分解高频区域中信号的详细信息[8]。在每一级信号分解时，除了对低频子带进行分解，也对高频子带进行分解。随着小波包分解的级数增加，其在频域上的分辨率就越高，因此，可以获取信号较高频率的信息分量。

小波函数通过尺度变量和平移变量平移、伸缩获得不同的频域和时间的位置，而小波包Ψji，k是小波函数φj的线性组合[9]：

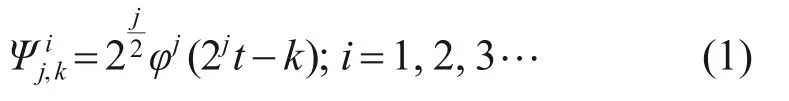
式中：i为调制参数；j为尺度参数；k为转换参数；t为时间参数。小波函数φj由式(2)和式(3)递归计算而得。

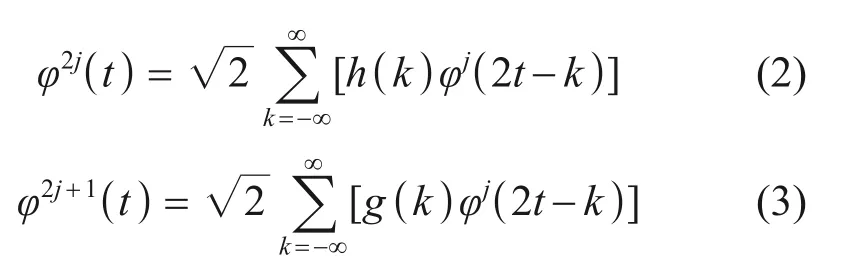
其中：h(k)和g(k)分别为与尺度函数和母小波函数关联的正交镜像低通滤波器和高通滤波器。在母小波函数中，Daubechies小波族函数具有较好的可逆性和正交性[10]，令φ1(t)=φ(t)建立母小波函数，得到满足可逆性和正交性的小波包函数Ψji，k。根据式(4)获得在分解等级z上的第u个节点处的小波包系数。由小波包的重构系数cuz，k(t)和小波包函数Ψji，k的线性组合得到小波包分量信号yuz(t)由式(5)给出[11]。

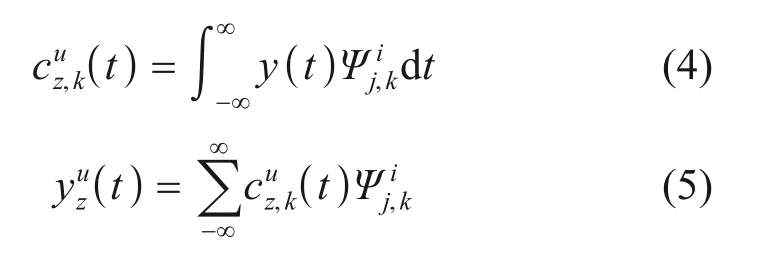
1.2 小波包能熵谱

当系统偏离正常状态时，信号的频率和幅值都将产生较大变化，熵值也会产生相应的变化[12]，并且将小波包和能量熵结合能更好地便于信号特征的提取。范数熵(norm entropy)是小波包能量熵的一种，设时间序列长度为n，对于单变量时间序列xt的范数熵可由式(6)计算可得：

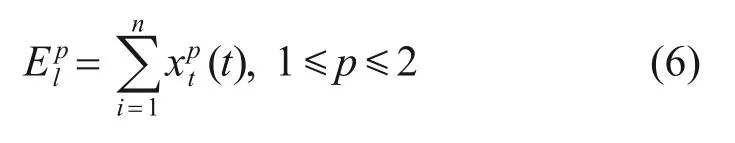
当p=2时，定义的范数熵可以用来代表信号的能量[13]。据此计算小波包分解和重构后各频带分量的时间离散序列yij的范数熵，选取高频分量中能量熵较高的前m个有效分量，忽略能量熵较低的分量，组成小波包能熵谱。小波包能熵谱中各频带的总能量熵E及各频带的能量占比νm由式(7)和(8)可得。

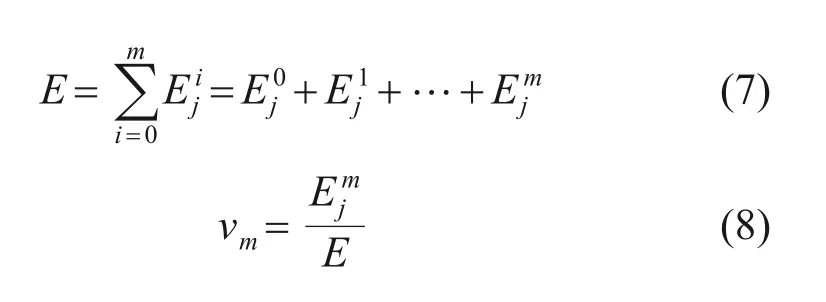
2 直喷煤油发动机爆震试验设计及数据处理

2.1 台架试验

爆震试验在1台自主设计开发的四冲程单缸航空煤油发动机上进行，煤油发动机的各项参数如表1所示。试验台架包括单缸试验煤油发动机、电力测功机、燃油供给系统、冷却系统、燃烧数据采集与分析系统、发动机电子控制系统以及上位机标定与控制系统组成。

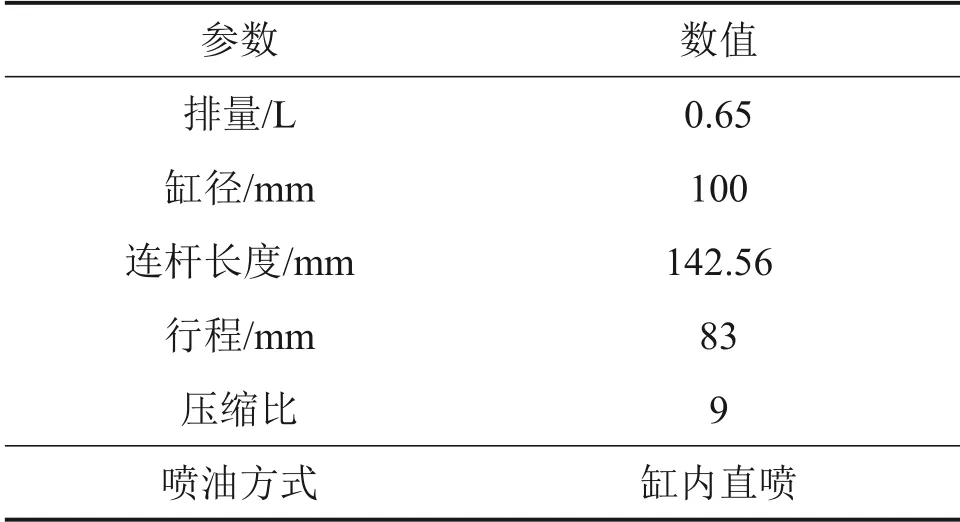
表1 单缸煤油发动机参数Table 1 Parameters of single-cylinder kerosene engine

试验中用于采集和分析缸内燃烧压力的设备有Kistler 6113C 型火花塞式压力传感器、Kistler 5011B型电荷放大器和德维创公司的DEWESoft X3燃烧分析仪。外时钟触发采样，外时钟频率与转速有关，为获取更加准确的爆震高频信号，缸压信号采集分辨率设置为0.1°。为了使爆震强度能够随着点火提前角的变化而发生显著变化，选取发动机中高速小负荷工况进行试验，试验工况参数如表2所示。在爆震试验过程中，通过上位机ECU标定软件增加点火提前角，以获得不同强度的爆震工况。

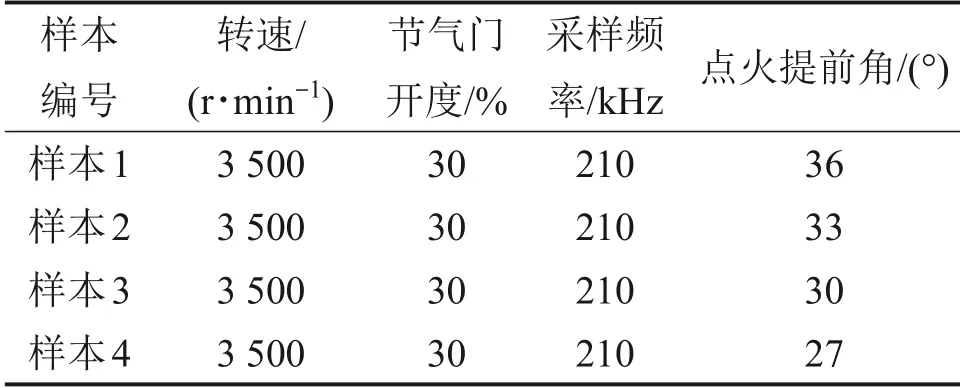
表2 爆震试验工况参数Table 2 Parameters of knock condition for test

2.2 小波包提取爆震压力高频分量及其能熵谱

爆震发生时，燃烧室的末端混合气自燃并释放出大量的能量，能量的快速释放将激发一系列特定的共振模式，即存在多个爆震频率中心。燃烧室中的共振频率取决于燃烧室的形状、尺寸和局部声速，可通过求解如下理论公式来估算[14]：

一天，我和表姐带晓玥出门逛街。路过的天桥上有一个满身泥巴的乞丐。晓玥老远就抓着我们的衣角，躲在我们身后，尽可能地远离乞丐。我们以为她嫌弃这个脏兮兮的乞丐，特意停下来给她2元硬币，要她送到乞丐的碗里去。她怯怯地走到乞丐跟前，小心地把硬币放进去，然后小跑着离开。我不禁感叹：孩子的童真和善良都被这个功利的社会吞噬了！

式中：ρη，δ为振动模态因子，下标η为切向模态数，下标δ为径向模态数；B为气缸直径；C为气体声速。本文使用的发动机内径B=100 mm，气体声速C=1 000 m/s。表3所示为爆震发生时不同共振模态下的预测频率。

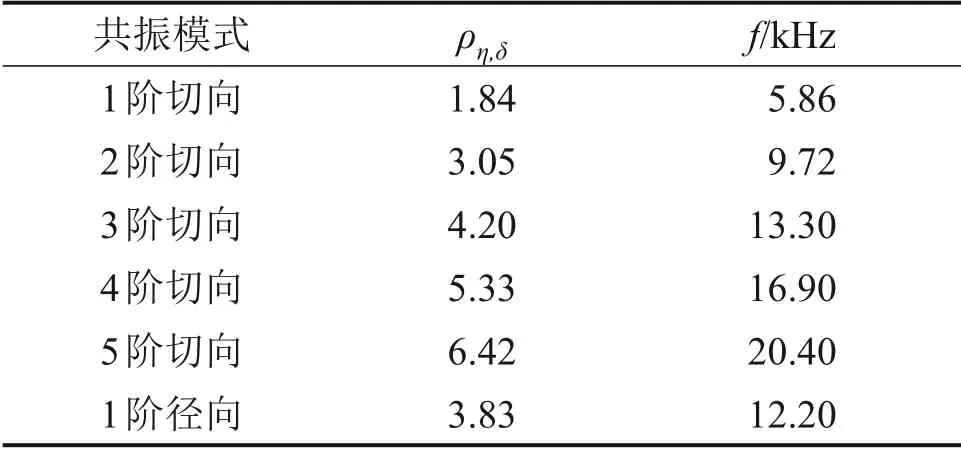
表3 圆柱形燃烧室不同振动模式下的理论频率Table 3 Theoretical frequency under different vibration modes of cylindrical combustion chamber

缸压信号的采样频率为210 kHz，在高频分量的提取过程中使用具有正交性和紧支撑性的db5小波函数[9]，本文依据表3中的爆震频带范围(5.86～20.4 kHz)使用6级小波包分解。经过每层分解，高频滤波部分在下采样后频谱发生翻转，导致频率顺序与节点顺序不同[15]，小波包分解树如图1所示。

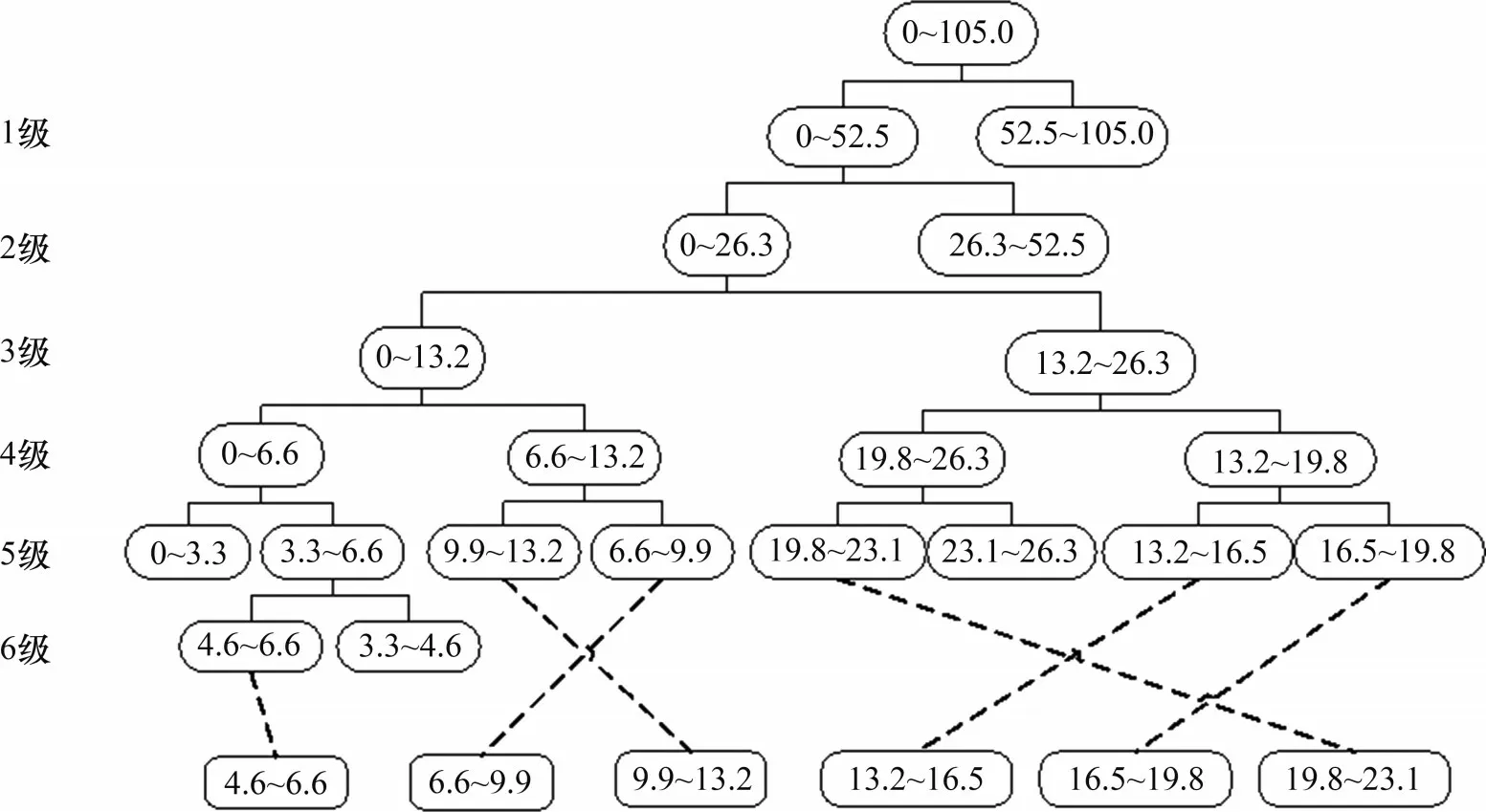
图1 六级小波包分解树Fig.1 Six-level wavelet packet decomposition tree

由于能量熵较小的小波包分量成分容易受到信号噪声的干扰，忽略26.3 kHz 以上的频率成分。根据表3中的理论频率选取6级小波包分解后的有效高频分量：d1(4.6～6.6 kHz)，d2(9.9～13.2 kHz)，d3(6.6～9.9 kHz)，d4(19.8～23.1 kHz)，d5(13.2～16.5 kHz)和d6(16.5～19.8 kHz)。取这6 个高频频带信号的范数能量熵构成小波包能熵谱。

图2所示为某一爆震循环的缸压信号分解得到的不同频带信号的时域图和频域图。图2(a)中每个频带信号是通过对原始缸压信号执行6级小波包分解和重构而得，图2(b)中频谱由快速傅里叶变换(FFT)获得。由图2(b)可知，小波包分解能够有效提取相应频带的信号。图3所示为由此爆震循环的高频频带d1～d6能量熵构建的能熵谱，揭示出爆震循环中各高频频带的能量分布情况。

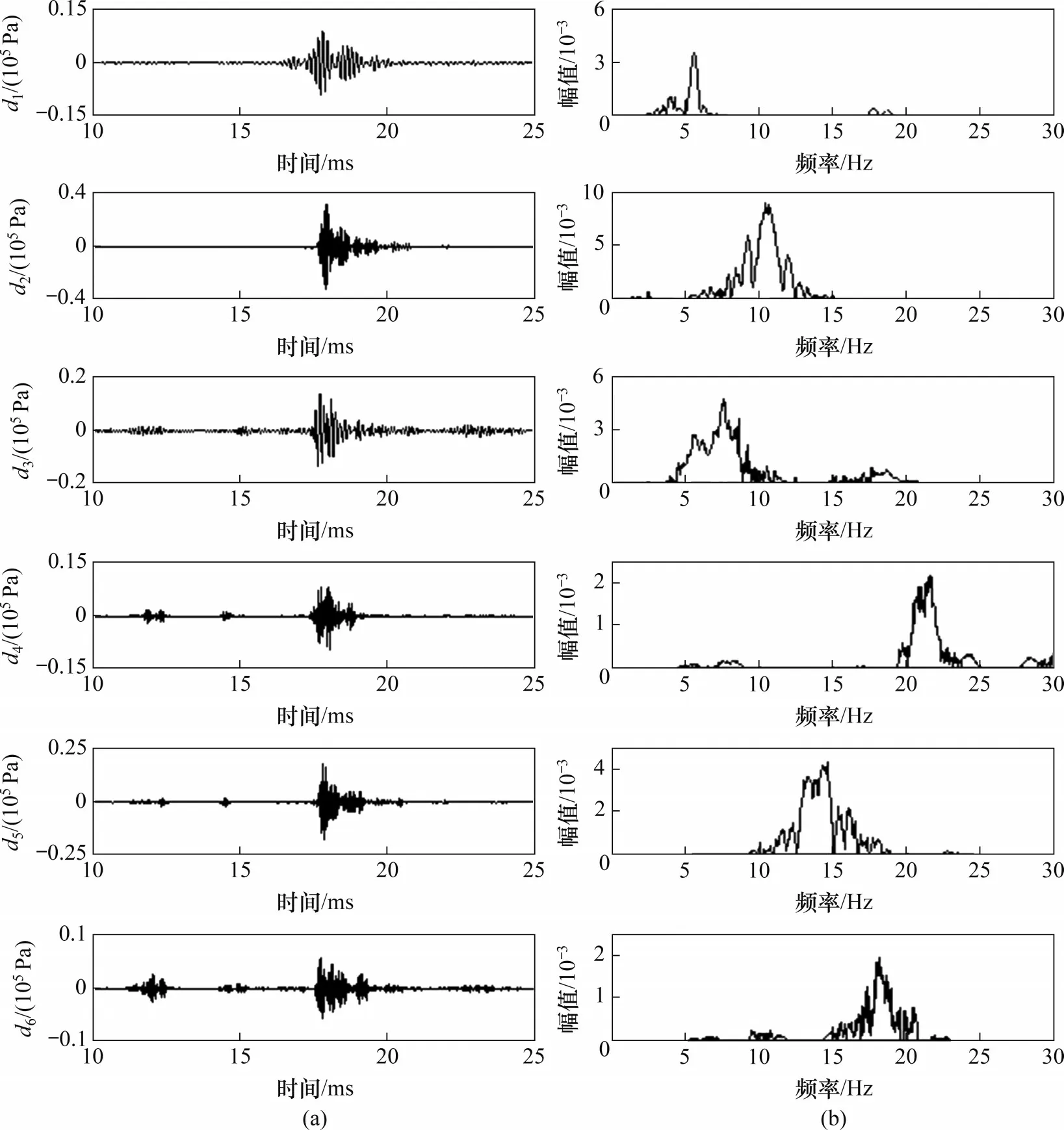
图2 六级小波包分解信号及其频率谱Fig.2 Six-level wavelet packet decomposition signal and its frequency spectrum

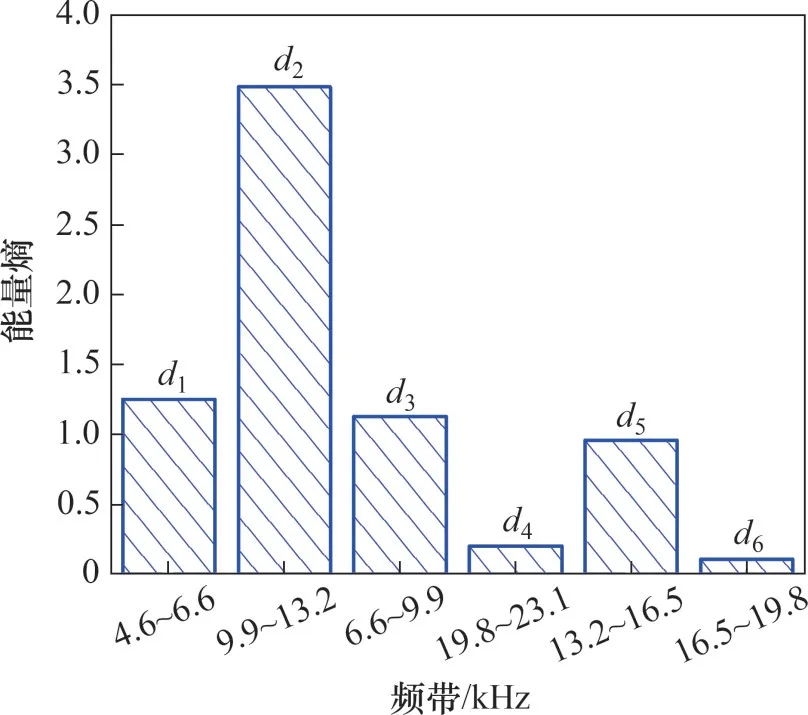
图3 缸压信号高频频带能量熵谱图Fig.3 Energy entropy spectrum diagram of high frequency band of cylinder pressure signal

3 基于小波包能熵谱的爆震分析

从试验获得的4组样本中，利用所采集到的循环缸压曲线基于Siemens VDO 爆震算法计算出爆震因子KF，然后，根据爆震因子KF的大小将爆震强度分为4个等级：严重爆震、中等爆震、轻微爆震、未爆震，如表4所示。由于爆震强度在循环间表现出随机特性，本文将从所得样本的统计值出发，探究爆震现象对小波包能熵谱中高频频带能量分布的影响，并提出一种新的表征爆震强度的指标。

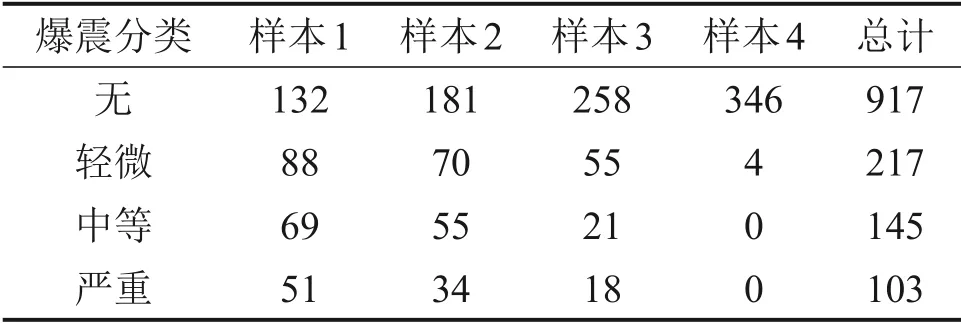
表4 爆震试验不同样本分类情况Table 4 Classification of different samples in knock test个

3.1 爆震强度对能熵谱特征的影响

图4所示为样本中所有不同爆震强度分类下的各频带能量占比的平均统计值。从能量成分上看，d1，d2，d3和d5是爆震频率的主要成分，即爆震能量主要集中在4.6～16.5 kHz频带内。从能量变化幅度上看，随着爆震强度的增加，频带d2(9.9～13.2 kHz)和d5(13.2～16.5 kHz)的能量占比不断增大，d3(6.6～9.9 kHz)和d6(16.5～19.8 kHz)的能量占比却不断下降，d1(4.6～6.6 kHz)和d4(19.8～23.1 kHz)的能量占比基本不变，不受爆震强度的影响。这说明不同频带能量对爆震的敏感性不同，d2和d5频带的能量增长幅度较大，受爆震影响最为显著，d1和d4次之。

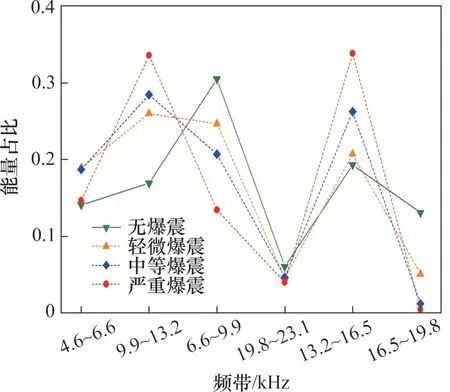
图4 不同爆震强度样本下各频带能量占比的平均统计值Fig.4 Average statistical value of energy ratio of each frequency band under different knock intensity samples

图5所示为样本1～3中各频带能量熵值的变化情况。从图5可知：无论何种爆震水平，爆震能量均主要分布在9.9～16.5 kHz的爆震频带。在同一点火提前角下，随着爆震等级的提升，各爆震频带的能量熵不断增加。点火提前角的不同，并不会改变频带能量的分布情况，这说明爆震特征频率与点火提前角无关。随着点火提前角增大，各频带具有更大的能量熵，这是因为点火角增加使得末端混合气在压缩行程末期温度和压力不断增加，自燃后瞬间释放出更多的热量，缸内燃烧压力急剧升高，在燃烧室内产生压力振荡冲击波导致出现更多的高频压力能量[16]。

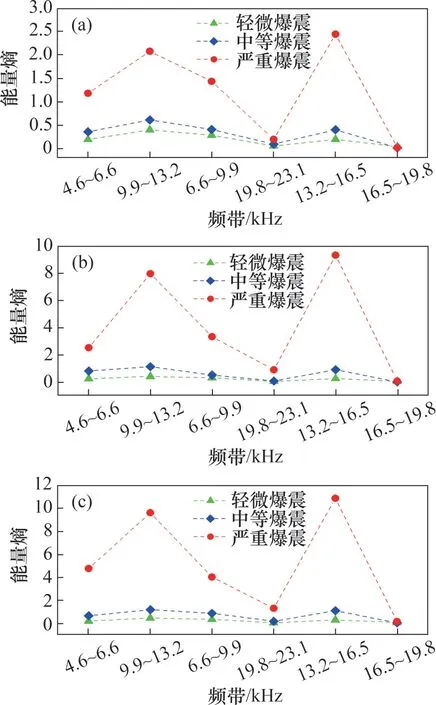
图5 不同点火提前角下爆震频带能量熵的样本统计值Fig.5 Sample statistical value of energy entropy of knock frequency band under different ignition advance angles

各频带的能量反映出爆震强度的等级，这主要是因为爆震发生的瞬间，可燃混合气自燃释放的热量越多，会产生更多的高频振荡压力能量，从而出现不同强度等级的爆震现象。值得注意的是，在d2(9.9～13.2 kHz)和d5(13.2～16.5 kHz)频带内的能量在发生严重爆震强度时明显增加，此频带与燃烧室一阶径向，二阶、三阶切向的理论共振频率相对应。

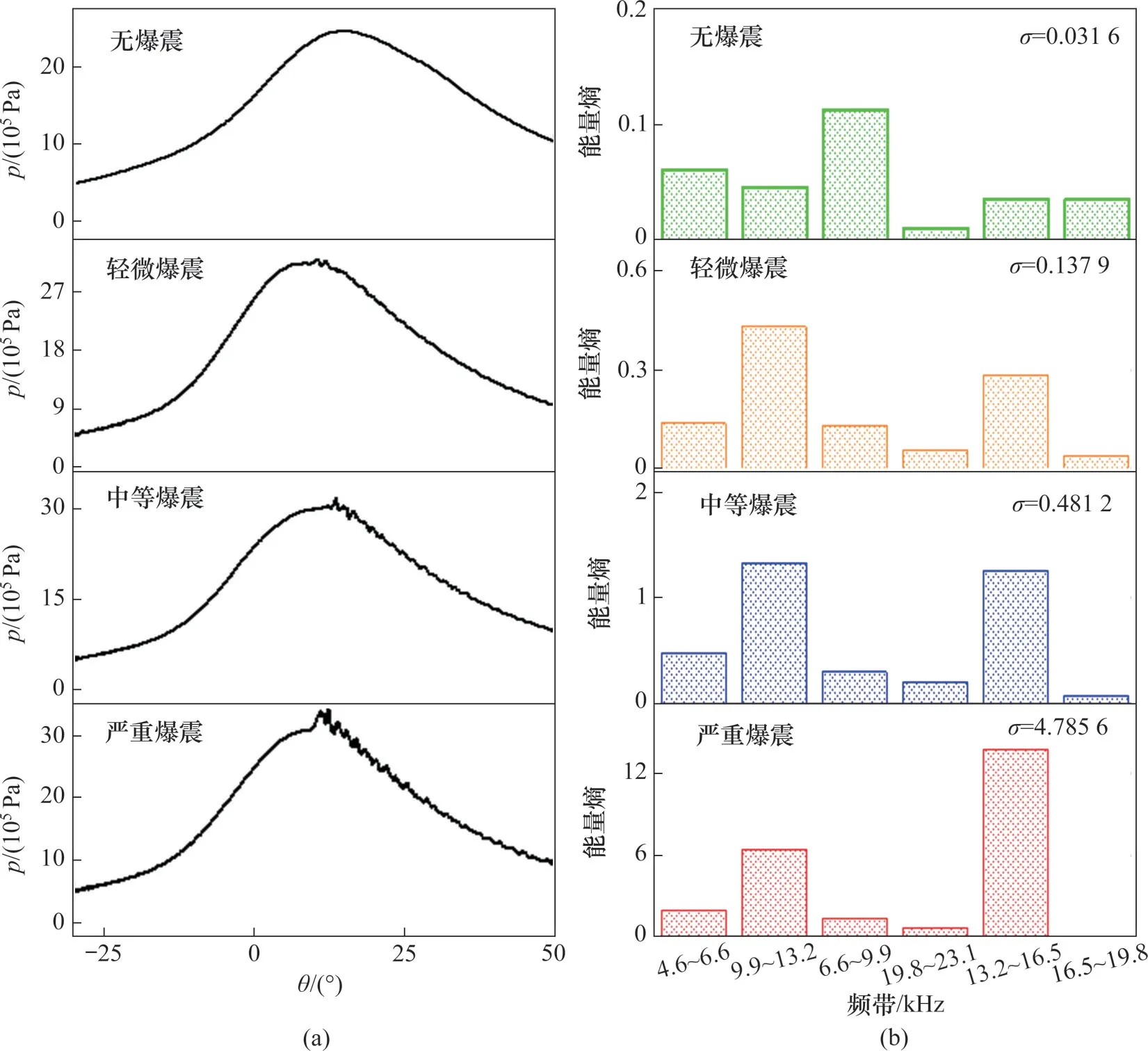
图6 不同爆震强度循环的缸压信号及其爆震频带能熵谱Fig.6 Cylinder pressure signal of different knock intensity cycles and its knock frequency band energy entropy spectrum

多个循环的样本统计值和单个循环样本的小波包能熵谱均能反映出此款煤油发动机的爆震特征频率为9.9～16.5 kHz；没有爆震发生时能熵谱中的能量分布较为均匀，爆震发生时能量分布发生明显变化，爆震特征频带9.9～16.5 kHz所具有的能量熵显著增加。

3.2 基于谱分析的爆震强度表征

不同的循环因为爆震强度不同，各个频带中能量熵最大值也发生相应变化。基于此现象，本文提出将小波包能熵谱中最大能量熵(the maximum of entropy,MOE)作为爆震发生的强度评价指标，即MOE 表征的是爆震时压力信号分布在各个高频频带中能量的最大值。为了检验爆震指标评价的效果，计算样本1～3的各个循环下的爆震指标。与使用Siemens VDO算法得到的爆震指标KF进行相关性检验[17]，并用最小二乘法线性拟合得到分布图，如图7所示。从图7可见：在不同爆震工况循环下，KF 和本文提出的MOE 指标的Pearson 相关系数r均在0.91之上，说明爆震指标KF和MOE指标具有高度的线性正相关关系，所以，MOE 同样能对爆震强度进行合理评价。

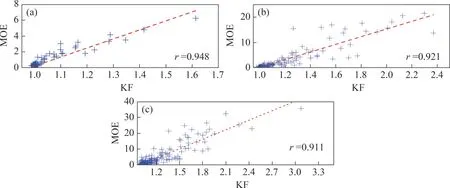
图7 样本1～3中各循环的MOE和KF相关性检验图Fig.7 Correlation test chart of MOE and KF for each cycle in samples 1-3

通过对爆震样本数据分析，爆震频带能量熵通常在频带d2(9.9～13.2 kHz)和d5(13.2～16.5 kHz)处取得最大值，即所提出的爆震指标反映的是与爆震相关特征频带的能量。相比于Siemens VDO 算法的准确度由爆震窗口宽度和起点确定，本文基于缸压信号提出的爆震表征指标MOE可以克服这一不足，且计算简便，对于点燃式发动机爆震强度评价具有一定的参考价值。

图8所示为点火提前角从27°增加到36°的4个样本的爆震强度评价指标MOE的分布图。从图8可以看出：从无爆震工况到爆震工况，评价指标MOE 能清晰地将不同爆震强度等级的工况区分出来，点火提前角增加至36°的过程中，爆震循环的比例逐渐提高。样本标准差(σ)逐渐增大，MOE分布更加离散，即爆震发生的频率增加；样本均值(μ)也不断增大，即高频压力分量的能量水平逐渐提高。这符合点燃式发动机爆震指标分布规律[18]。处于爆震临界状态的循环位于图8中红色方框内，此区域内的MOE 在0.3～0.4 之间，既有无爆震循环，又有轻微爆震循环。

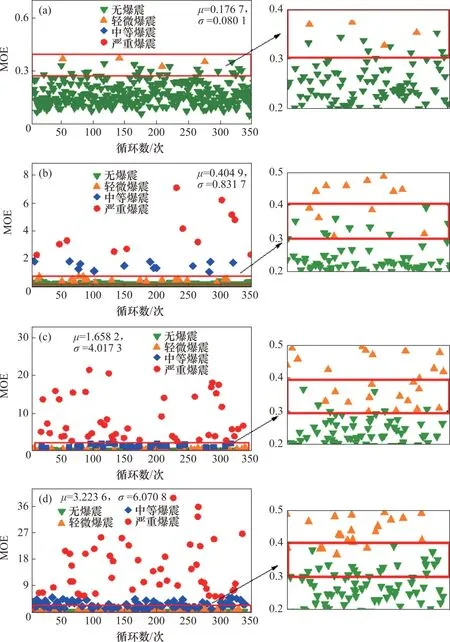
图8 无爆震至爆震工况中各循环的MOE分布图Fig.8 MOE distribution of each cycle from knock-free to knock conditions

划定合理的阈值会减少爆震检测的错误发生率，本文通过ROC 曲线评估不同阈值对爆震检测的准确率。从0.3开始每隔0.05设置爆震阈值，检测的负正类率(false positive rate，FPR)和真正类率(true positive rate，TPR)会随之改变，观测结果如图9所示。从图9可见：爆震阈值设置在0.355 时曲线出现转折，识别出真正类的比例达到94.22%，设置的爆震阈值减小会使负正类率FPR陡然上升，正确检测概率TPR 趋缓，故将MOE 设置为0.355时，在当前工况下，爆震检测有较高的正确率。需要指出的是，在不同工况下，爆震阈值有所不同，需要经过试验标定确定合适的阈值。

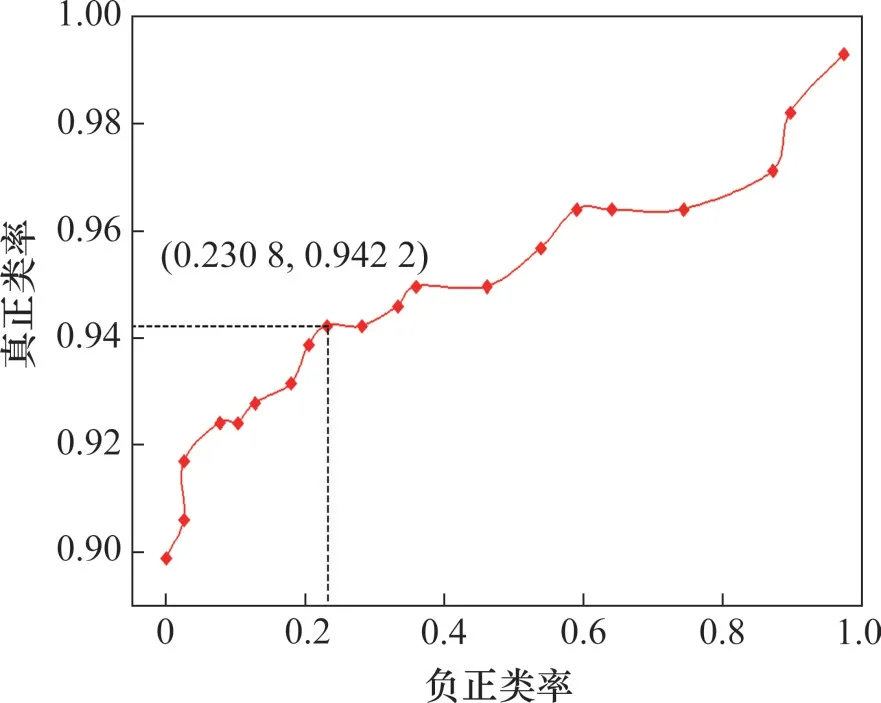
图9 不同爆震阈值对应的正误率ROC曲线Fig.9 ROC curve of correct error rate correspond-ing to different knock thresholds

4 结论

1)通过小波包分解和重构算法可以提取爆震发生时不同频带下的高频压力信号，进而获得小波包能熵谱。该方法为分析爆震各频带的能量变化提供了有效的途径。

2)爆震能量主要集中在4.6～16.5 kHz高频压力内。当爆震强度增加时，小波包各频带分量的能量熵值及其分布会受到影响，9.9～13.2 kHz 和13.2～16.5 kHz 频带能量熵增长迅速，随着爆震的发生而出现明显的变化。

3)本文提出的爆震评价指标MOE 与Siemens VDO 算法计算得到的爆震因子(KF)有较好的相关性，可以作为爆震强度的评价指标。在此款煤油发动机上，在试验工况下，MOE处于0.3～0.4为爆震临界区间，利用ROC 曲线估计时，将爆震阈值设置为0.355作为爆震监测条件更合适。