基于AHP层次分析法的高校学生干部选拔体系探究

阮文杰, 葛克伟, 李建龙

(扬州职业大学, 江苏 扬州 225009)

高校学生干部是高校管理中极为重要的组成部分,优秀的学生干部团队,对营造优良的学风、校风以及创建和谐积极的校园氛围有着重要作用。将层次分析法应用到学生干部选拔综合素质评价系统中,有利于控制由于评价者的主观因素或情绪化倾向而导致的决策不全面问题,将定性的指标尽可能定量化,推进学生干部选拔体系客观化、科学化、系统化进程。

1 层次分析法简介

层次分析法是将与决策有关的元素分解成目标、准则、方案等层次,在此基础之上进行定性和定量分析的决策方法[1]。在利用层次分析法进行众多主观性问题的决策分析时,首先要把问题客观化、层次化、系统化,构造出一个富有多重结构层次的数学矩阵模型,并逐层建立具有直接影响关系的矩阵结构。众多决策者组成的评审团,系统、全面、客观地评估各要素在不同层次结构中所占的层级位置,将这些元素按目标、准则、方案等属性关系构成若干层次结构。按下一层次元素对上一层次的有关元素所占的重要程度,对各层级的组成要素进行相互评价。层次分析法可将这些相互评价转换为在不同分类结构中的比较权重,这些权重形成相对优先级。利用 1—9 度法(见表1)对结构中的每层指标进行两两比较,构建出判断矩阵。计算矩阵的最大特征值对应的特征向量,即为各指标的权重值。这一系列数值可导入学生干部选拔综合素质评价系统中进行数学模型的运算,为最终的学生干部选拔人选提供精准的指导意见。

表1 1—9度法评价标度

2 学生干部综合素质评价模型的构建

评价模型在构建时要遵循全面性原则、层次性原则、拓展性原则、兼容性原则和可行性原则。模型构建时，首先由熟悉学生工作的若干位老师、辅导员、学生会干部组成评审团,对评价体系进行方案讨论、指标分析、层次划分。初步确定了三个评价方向,分别是专业学习能力(B1)、思想道德素质(B2)、工作实践能力(B3),这三个方向作为评价模型的一级评价指标。这三个一级评价指标下又包含十个二级评价指标(见图1)，覆盖了被选拔学生干部的基本素质和能力素质的各个方面,体现了学生干部选拔综合素质评价模型的系统性和全面性。

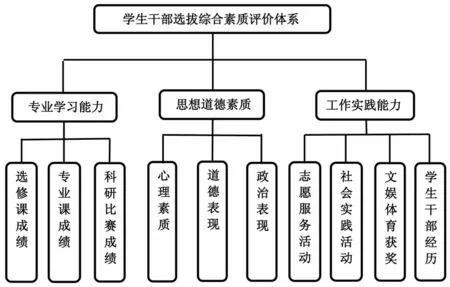
图1 学生干部综合素质评价模型

将学生干部综合素质评价体系的评价指标按积分标准和积分细则转化为学生干部素质评分(见表2),这些积分覆盖了在校期间与学生基本素质和综合素质相关的能力,为进一步进行量化计算提供客观数据支撑。

表2 学生干部素质评分表

3 层次分析法在综合素质评价模型中的应用

3.1 综合素质评价模型矩阵构建及计算

在高校全方位育人的背景下,通过决策者组成的评审团,经多方讨论并投票,最终确定：对于目标层来说,准则层的工作实践能力(B3)比思想道德素质 (B2) 略微重要,根据1—9度法评价标度,Saaty标度因子为3；思想道德素质(B2) 比专业学习能力(B1)略微重要,同样Saaty标度因子为3；工作实践能力(B3)比专业学习能力(B1)重要,Saaty标度因子为5,因此得出的第一个判断矩阵如下:

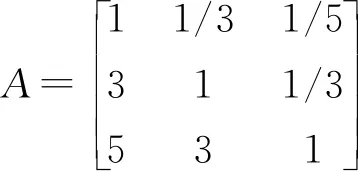
经特征根法进行矩阵运算,计算特征向量的权重系数为WA=(0.106,0.260,0.633)T(见表3)。在计算出最大特征值λmax的基础上进行一致性检验,令CI=(λmax-n)/(n-1),在这里CI为一致性指数。根据相对一致性指标:CR=CI/RI,CR称为一致性比率,RI称为随机指数。一般情况下,当CR<0.1时,可判断为误差较小,一致性可以接受。如比率大于0.1,则说明没通过一致性的检验,要对照矩阵进行逐一检查修改,重新进行计算,直到一致性检验合格。

表3 判断矩阵A及权重WA

对矩阵进行运算求解,经计算最大特征值λmax=3.039,并对判断矩阵A做一致性检验。在判断矩阵中,经最大特征值的一致性指数计算求得CI=0.019,根据RI数值表可查(见表4),RI=0.58,CR=CI/RI=0.033<0.1。比率小于0.1,判断矩阵的一致性检验合格。因此该判断矩阵所得权重向量有效,具有合格的一致性,也就是说权重W是客观和可被接受的。一般学术界认为,不同阶数的倒数矩阵产生不同的一致性指数值。同一阶数矩阵的一致性指数值在大数法则下趋于稳定,逐步接近随机指数值[2]。

表4 RI数值表

同理,经评审团会议商议讨论并投票,确定对于一级指标层专业学习能力(B1)来说,二级指标层中的专业课成绩(C12)比选修课成绩(C11) 重要,科研比赛成绩(C13)与专业课成绩(C12)同样重要,科研比赛成绩(C13) 比选修课成绩(C11)较重要,因此得出的第二个判断矩阵如下:

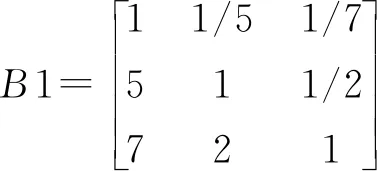
经特征根法进行矩阵运算,计算特征向量的权重系数为W=(0.078,0.435,0.487)T(见表5),在计算出最大特征值λmax的基础上进行一致性检验。

表5 判断矩阵B1及权重W1

对矩阵进行运算求解,计算得最大特征值λmax=3.013,并对判断矩阵B1做一致性检验:令CI=(λmax-n)/(n-1)=0.006,根据RI数值表可查,RI=0.58,在B1判断矩阵中,经检验判断矩阵的权重向量求得CR=CI/RI=0.011<0.1,判断矩阵的一致性可以接受。

同理,对于一级指标层的思想道德素质(B2)来说,二级指标层中的道德表现(C22)比心理素质(C21)略微重要,政治表现(C23) 和道德表现(C12)同样重要,政治表现(C23) 对心理素质(C21)的重要性介于略微重要与重要之间,因此得出第三个判断矩阵如下:

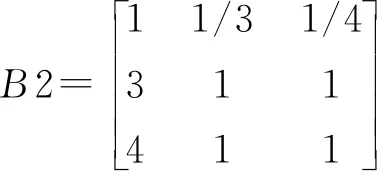
经特征根法进行矩阵运算,计算特征向量的权重系数为W=(0.126,0.416,0.458)T(见表6),在计算出最大特征值λmax的基础上进行一致性检验。

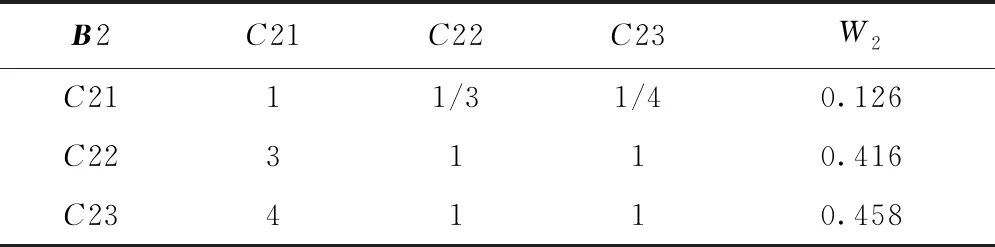
表6 判断矩阵B2及权重W2

对矩阵进行运算求解,经计算最大特征值λmax=3.009,并对判断矩阵B2做一致性检验:令CI=(λmax-n)/(n-1)=0.005,根据RI数值表可查,RI=0.58,在B2判断矩阵中,经检验判断矩阵的权重向量求得CR=CI/RI=0.008<0.1,判断矩阵的一致性可以接受。

同理,对于一级指标层的工作实践能力(B3)来说,二级指标层中的社会实践活动(C32)对志愿服务活动(C31)的重要性介于相同与略微重要之间,文体活动获奖(C33) 比志愿服务活动(C31)略微重要,学生干部经历(C34)比志愿服务活动(C31)重要,文体活动获奖(C33)对社会实践活动(C32)的重要性介于相同与略微重要之间,学生干部经历(C34)比社会实践活动(C32)重要,学生干部经历(C34)对文体活动获奖(C33)的重要性介于相同与略微重要之间,因此得出的第四个判断矩阵如下:

根据特征根法进行矩阵运算,计算得特征向量的权重系数为W=(0.090,0.158,0.268,0.484)T(见表7),在计算出最大特征值λmax的基础上进行一致性检验。

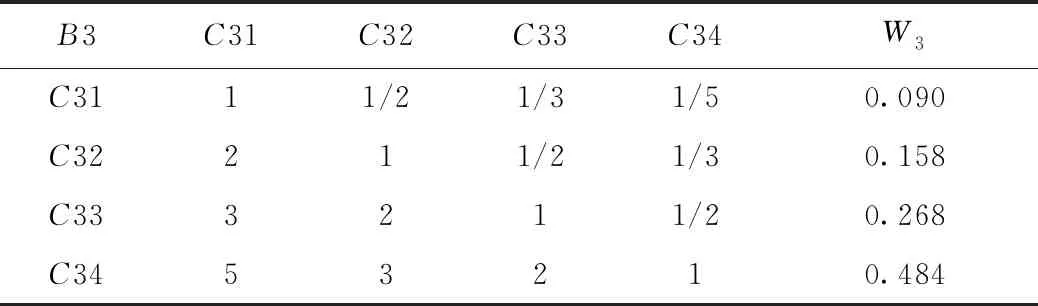
表7 判断矩阵B3及权重W3

对矩阵进行运算求解,经计算最大特征值λmax=4.015,并对判断矩阵B3做一致性检验:令CI=(λmax-n)/(n-1)=0.005,根据RI数值表可查RI=0.90,在B3判断矩阵中,经检验判断矩阵的权重向量求得CR=CI/RI=0.006<0.1,判断矩阵的一致性可以接受。

经计算,四个矩阵一致性判定均检验合格,说明在构建学生干部选拔综合素质评价体系中各层各级的评价指标和矩阵关系具有一定的科学性和合理性,符合当初设计构想。

3.2 模型指标数据的来源

实例验证中,以扬州市某大学某次学生会选拔甲、乙、丙三位学生干部考核为例,利用本次创建的学生干部选拔综合素质评价模型和计算得出的评价指标权重进行分析。

首先，召集学生工作负责人、辅导员、上届学生会主要干部等有关人员组成评审团进行专题会议。在会议上由三名学生干部做自我介绍并提供相应的成绩、获奖情况、参与活动的证明等相关材料,通过对评价体系进行模型讲解、指标分析、数据审核,在评审团充分理解学生干部选拔综合素质评价模型的指标含义、运算规则、权重加成的基础上,发放学生干部选拔综合素质测评表,评审团分别对模型中10个二级子指标进行打分,各项指标打分为百分制,分值范围为0～100 分,权重W的数值由WA与W1、W2、W3分别相乘得到(见表8)。

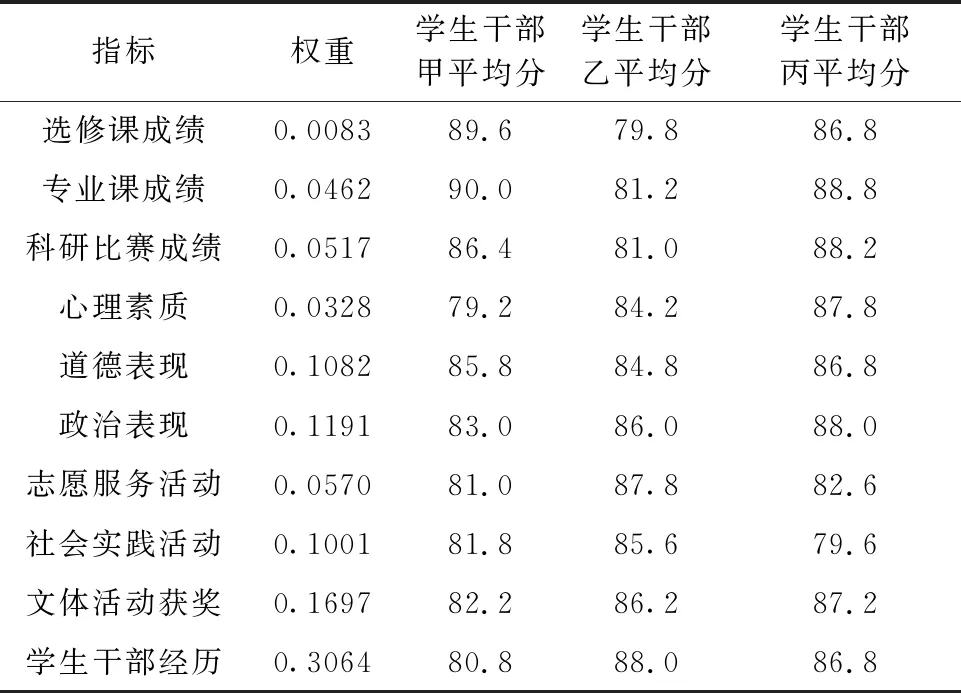
表8 学生干部甲、乙、丙选拔测评表

3.3 模型计算结果

将各准则层的指标平均分与权重系数相乘,最后加总可得出学生干部候选人的最终得分。学生干部甲虽然学习成绩很好,但由于占学生干部选拔权重更高的工作实践能力评分不高,导致最终得分为82.6046分。学生干部乙学习成绩上虽然不突出,但参加实践活动较多,心理素质较好,得分为85.9038分,反而高于学生甲。学生干部丙志愿服务活动和社会实践活动得分相对较低,但专业学习能力和思想道德素质相对较高,占权重最大的二级指标学生干部经历也和学生干部乙相差无几,最终得分为86.1618分,综合素质评价还要比学生乙略高一筹。

通过实例运用可以看出,利用层次分析法能同时分析的评价模型样本数量远远大于上述三例,完全能够满足学生干部选拔的需要。为避免举例中数据冗长,分析复杂,过程繁琐,故提取样本数量从简,未将所有参与选拔的学生纳入评价模型中进行计算。

4 层次分析法构建评价体系的优缺点及对策

层次分析法是对定性问题进行定量化分析的一种多重准则判定方法,将定性问题在一定程度上转化为定量分析,可以克服传统学生干部在选拔考核时人为判断的主观性问题[3]。层次分析法所构建的学生干部选拔综合素质评价体系,使得各项评价指标的权重不再由人工赋予,而是取决于学生之间在某个考核内容上的相对优劣,即相互之间“优秀”的相对程度,对于构建学生干部选拔评价体系是一种行之有效的方法。

4.1 层次分析法评价体系优点

通过学生干部选拔评价体系模型计算得出的结论可以更全面系统地把握所有参与选拔的学生干部情况。由于是通过相对客观的数据构建的数学模型,运算得到的结果也相对客观,更容易得到评委老师、学生干部、同学们的认可和接受。

应用选拔评价体系后的结果反馈,被选拔的学生干部不仅可以获得来自老师和同学对自己的专业学习能力、思想道德素质、工作实践能力等方面的直观评价,也可以较全面、客观地了解自己在学习、生活和工作中的优缺点。

4.2 层次分析法评价体系缺点

在评审过程中,不同评审者与被选拔的学生交流接触的范围不同,对被选拔学生的观察角度不一样,很难做到对其本人有很客观全面的认识,从而使得部分指标客观性失真。评审者对评价指标的认知和理解,也会对评价过程和评价体系运算有所影响。在选拔过程中,被选拔者与评审者处于一个动态复杂的人际关系之中,评审者的感情因素、主观行为等同样会使原始量化指标的客观性受到一定程度的影响,进而影响到最终的计算结果。

众所周知,在设置学生干部选拔体系评价指标时,所设指标不可能覆盖体系中选拔对象的所有方面,必须做出有效取舍,如想尽可能地接近客观实际,需要增加各层各级众多数量的指标,但这样势必增加数据计算的复杂程度和评价指标权重的获取难度,使得层次分析法的实用功能和便捷性消失殆尽。因此,结合相关经验数据和评审团专家意见,选取出相对合适重要的指标,得出最大可能的代表性评价数据将是下一步研究的课题。

4.3 层次分析法评价体系再思考的对策建议

为降低评价者主观因素对评价对象的影响,笔者构想将来利用改进型的层次分析方法对评价体系重新进行权重分配。通过评审者之间的利益评价指标,构建评审者价值矩阵,计算出所有评审者特征向量的权重系数,然后将所得到的评审者价值权重与传统层次分析法得到的指标权重进行加权平均,最后将学生各方面素质得分与评价体系权重进行加权平均,综合计算出学生干部的综合素质得分。这样能够有效避免评审专家基于自身感情倾向对学生干部选拔做出主观性判断。

构建学生干部选拔综合素质评价体系要符合各学校特点和发展层次,各校应根据自身情况进行相应的指标调整和模型改进。该方法尚在实践研究的初步阶段,今后将通过大量样本实践数据研究,检验该模型应用于不同专业、不同层次的应用环境下的可行性,为科学有效地建立学生干部选拔评价体系提供新的思路和途径。