不同卫星截止高度角下GPS观测结果的对比分析

龚 俊 戴煜暄 曾利萍

(1. 浙江省地震局, 浙江 杭州 310013; 2. 浙江省测绘科学技术研究院, 浙江 杭州 311100)

0 引言

长期连续的全球定位系统(global positioning system,GPS)观测是获得区域和全球地壳精细动态变化信息的主要方法之一,规范[1]要求测站位置各方向视线高度角15°以上应无阻挡。特殊困难地区,经项目主管单位批准可在一定范围内(水平视角不超过60°)放宽至25°。在GPS数据精密后处理中,一般设置的卫星截止高度角为15°。但在实际中由于条件所限,有时只能在不满足规范要求的地方建设台站,由于高度角无法满足15°的要求而放弃建设是否恰当;同时对于地壳运动研究来说,GPS观测时间长度如果小于2.5 a,由坐标时间序列得到速度估计的偏差将不可接受,而大于4.5 a的时间长度速度估计的偏差可以忽略[2],不同卫星截止高度角对于长期GPS观测得到的误差、噪声、速度等地壳运动相关信息有什么差异。由于GPS台站在0°—5°卫星截止高度角的卫星信号非常容易受到遮挡和多路径效应的干扰,因此本文对浙江省地壳形变观测网时间跨度为4.2年的GPS数据在5°、10°、15°、20°、25°、30°和35°不同卫星截止高度角下GPS数据进行了研究,以期能提供一些相关的信息。

1 区域构造及监测台网概况

浙江省陆域面积101 800 km2,地处中国大陆东部,地势由西南向东北倾斜,呈阶梯下降,西南是山地,中部是丘陵和山地,东北是平原。中国大陆东部岩石圈具有相当的强度,其构造运动表现为刚性块体的相对运动,内部形变很小,构造稳定[3]。浙江省地震局在“十五”期间开始建设服务于地震监测预报,以全球导航卫星系统(global navigation satellite system，GNSS)观测为主的浙江省地壳运动监测网络,现有23个基准站(含3个中国大陆构造环境监测网络的台站)。

2 模型与算法

2.1 GPS数据处理及分析方法

GPS数据处理采用高精度数据处理软件GNSS在麻省理工学院(GNSS at MIT,GAMIT)计算2016—2020年浙江省地壳形变观测网络基准站坐标和卫星轨道的单日松弛解,同时引入国内及周边25个国际GNSS服务组织(The International GNSS Service,IGS)跟踪站进行同步计算,然后把得到的单日松弛解文件与IGS提供的全球9个子网的单日松弛解文件联合,利用全局卡尔曼滤波器(global Kalman filter,GLOBK)软件进行Kalman滤波,并删除因观测环境、接收机内部噪声等原因造成的少数离群值。

2.2 不同卫星截止高度角GPS双差观测数的差异

GAMIT以星间求差以及站间求差方法得到的双差相位观测量进行解算,双差方式可以消除接收机钟差、卫星钟差等未知参数,削弱大气延迟等影响。GAMIT解算过程记录的q文件有对解算精度和可靠性进行评估的指标,同时有各台站每颗卫星的双差观测数。对各个台站在不同卫星截止高度角下每颗卫星平均的双差观测数进行统计,以站网中视野开阔的湖州基准站计算不同卫星截止高度角在4.2 a时间下每颗卫星平均的双差观测数为例,得到表1。

表1 湖州基准站在不同卫星截止高度角下每颗卫星平均的双差观测数

使用阿努比斯(Anubis)软件[4]绘制2020年1月1日湖州基准站的俄罗斯全球卫星导航系统(global navigation satellite system,GLONASS)和GPS的卫星运行轨迹图(图1)。

图1 卫星运行轨迹(方位角-高度角)

从图1看出湖州基准站在5°以上卫星截止高度角可以保证GPS数据完全的接收,同时由表1中可以得出卫星截止高度角每增加5°,每颗卫星平均的双差观测数相对15°时的观测数减少12%左右。

2.3 GPS坐标时间序列模型

假设GPS台站的时间序列是由确定性的模型和随机噪声组成,确定性的模型可由式(1)[5]表示。

(1)

2.4 GPS坐标时间序列噪声模型

GPS时间序列存在时间相关性,以往的研究表明,GPS位置时间序列作为一种地球物理学现象,其观测噪声可以描述为幂律过程或具有功率谱形式的时域行为[6]，见式(2)。

(2)

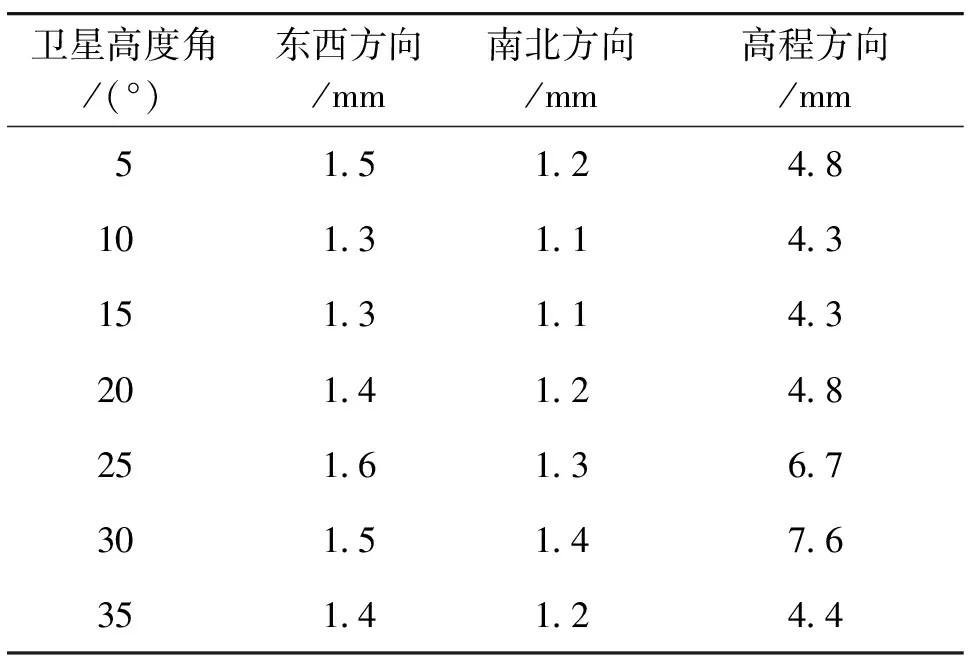
式中,f是时间频率;P0和f0是常数;k是谱指数,由于地球物理现象的噪声特性以低频为主,k越小,表示噪声与时间的相关性越高。通常,谱指数k在[-3,1]范围内,当-1

根据前人的研究结果,最大似然估计能较真实的反映时间序列中的噪声模型,同时可以使用不同的噪声模型组合进行分析,其中白噪声加上闪烁噪声为针对全球GPS台站的最佳模型[7]。为了分析不同噪声模型在时间序列参数估计的占比,本研究使用两种组合进行分析:第一种组合仅考虑白噪声(white noise,WN),而第二种组合同时考虑白噪声、闪烁噪声(flicker noise,FN)和随机游走噪声(random walk noise,RWN)。使用CATS软件[8]在两种组合下分别估计了不同卫星截止高度角下对各台站坐标时间序列的白噪声、闪烁噪声和随机游走噪声分量的大小(图2)。

(a)东西方向

(b)南北方向

(c)高程方向

由图2可以看出,组合一中的白噪声量级大于组合二中的白噪声量级,但明显小于组合二中3种噪声量级的和,两种组合噪声的量级相差2～3倍,说明在进行时间序列分析时如果仅考虑白噪声会高估白噪声,并大大低估时间序列中的总噪声。同时闪烁噪声在3种噪声中占比最大,因此在进行GPS时间序列噪声分析时一定要考虑闪烁噪声,当只考虑两种噪声时白噪声加上闪烁噪声是最佳的噪声模型。

同时可以看出当卫星截止高度角在10°、15°和35°时噪声相对较低,其中35°卫星截止高度角噪声最低。可能的原因是在所研究的23个台站中,部分台站受到短时的遮挡和多路径的影响,而当卫星截止高度角为35°时,虽然每颗卫星平均的双差观测数只相当于15°高度角观测数的一半,但对以天为单元的连续观测来说已经可以得到稳定的结果,同时35°的高度角受到遮挡和多路径影响最小,所以噪声量级最低,因此在保证观测数据量时,高度角越高噪声越低。

2.5 GPS坐标时间序列观测精度分析

在工程形变和地壳形变测量中,常进行定期重复测量,如果考虑工程或地壳的运动变化,在评定实测精度时需排除这种运动变化的影响,在这种情况下,要对测量结果x1,x2,…,xn作一次差分,以消除母体移动的影响,按下式也就是均方连差公式估计测量精度[9](记为q):

式中,q是观测精度的无偏估计[10]。由于GAMIT/GLOBK得到的ENU坐标是在ITRF2014框架下的坐标,属于动态的系统,因此采用均分连差公式进行估计,得到各台站东西、南北和高程3个方向的均方连差精度的均值,得到表2。

表2 不同卫星截止高度角下3个方向的精度表

从表2可以看出,东西方向的观测精度低于南北方向。相对来说在10°、15°和35°的卫星截止高度角下,3个方向的精度较为一致。

2.6 不同卫星截止高度角速度解算的差异

完整、可靠的地壳运动速度场是对构造变形的定量描述,是地球动力学的关键之一[11],采用2.3节中白噪声、闪烁噪声和随机游走噪声模型得到23个基准站GPS结果的速度解,表3展示各个基准站在不同卫星截止高度角下的结果。

表3 不同卫星截止高度角下的速度结果 单位：mm/a

由于GPS台站的速度值是与框架相关的,因此对于一个台站来说并不存在一个绝对正确的速度值可以作为参考,因此以各个台站在不同卫星高度角下得到速度值最大值和最小值的极差作为不同卫星截止高度角下速度值差异的一个研究指标,得到表4。

表4 各个台站在不同卫星截止高度角下3个方向速度值的极差

从表4可以看出大部分台站水平方向速度的极差小于表3中速度误差值的两倍平均中误差,差异并不明显,但对于部分在观测过程受到过多路径影响(江山、余杭、庆元、义乌、卓山)和天线移动(南山头)影响的台站来说极差相对较大。因此就本次研究来说,在没有多路径等外部条件影响下,对于长期观测来说不同卫星截止高度角下的水平速度的差异不大。

3 结束语

对2016年至2020年浙江省地壳形变观测网络在5°、10°、15°、20°、25°、30°和35°卫星截止高度角下的GPS数据进行分析,从各项指标来看:卫星截止高度角增加5度,每颗卫星平均的双差观测数减少12%左右;10°、15°和35°时噪声相对较低,相对来说35°卫星截止高度角噪声最低;在保证观测数据量时,高度角越高噪声越低;东西方向的观测精度低于南北方向,相对来说在10°、15°和35°的卫星截止高度角下,3个方向的精度较为一致;在没有遮挡和多路径等外部条件影响下,对于长期观测来说,5°～35°不同卫星截止高度角下的水平速度的差异不大。