基于多变量自学习与融合策略的多视图聚类算法*

尚晓群 杨海峰 蔡江辉

（太原科技大学计算机科学与技术学院 太原 030024）

1 引言

来自不同数据源的数据类型（如文本、图像、视频等）描述同一对象或主题，形成了多视图数据［1～3］。例如，一个多媒体片段可由视频信号和音频信号同时描述；一个网页的特征可通过文档文本、超链接、图片信息等表示；一张图片可通过不同的特征提取器捕获其相应的表示，如LBP、SIFT、HOG等。多视图数据的爆炸性增长，引发了对其进行有效分析和处理的技术需求增长。在数据挖掘中，聚类分析［4］是一项非常重要的技术，能将相似度高的数据划分到一个簇。在过去的几十年里，许多的聚类方法已经被发展，如K-means，谱聚类，基于核的聚类方法，基于图的聚类方法和基于密度的聚类方法。旨在利用跨视图间数据的互补性和一致性信息，多视图聚类方法［5～6］已引起广泛的关注。

现有的多视图聚类方法主要分为五类：协同训练风格算法、多核学习、多视图图形聚类、多视图子空间聚类、多任务多视图聚类［7］。此外，多视图图形聚类被进一步划分为基于图形、基于网络和基于谱论；多视图子空间聚类被进一步划分为基于子空间学习和基于非负矩阵分解。由于多视图聚类的可扩展性，许多学者做了进一步的研究。杨敏申等［8］在k-means 聚类过程中进行特征降维，改进了多视图k-means聚类。王浩等［9］对基于图形的多视图聚类在通用方法和图形度量两个方面进行研究，提出了一个基于图形的多视图聚类系统GBS。

尽管现有的多视图聚类算法已在不同方面被改进与完善，且取得了不错的聚类结果，但是，合理挖掘视图的一致性信息和互补性信息依然是目前多视图聚类研究的难题与挑战。针对这个问题，本文提出一种新颖的多视图聚类算法MSFC，基于多变量自学习与融合策略过程如图1 所示，该算法自学习数据集对应的视图内全局变量、视图内局部变量和视图间变量，并将其整体投射于一个相似性度量函数，获取融合矩阵，以得到更加准确的聚类结果。

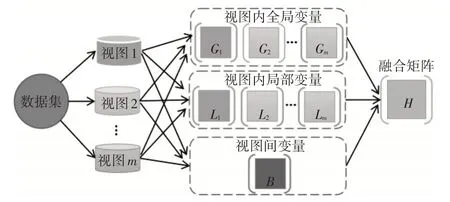
图1 基于多变量自学习与融合策略过程

2 理论基础

2.1 信息熵

信息熵［10～11］是一种信息的度量化方法，基本思想是：用信息量度量信息的多少，再对产生的信息量作期望。对于一个离散随机变量X，所有状态为｛x1，x2，…，xn｝，当状态为xi时，对应的概率为pi，则X的信息熵可以被定义为

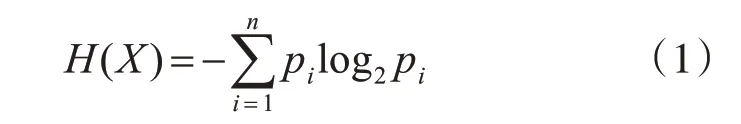
其中不确定性函数H 是概率pi的减函数，即当概率大时，不确定性小；反之，不确定性就大。信息熵反映了离散随机事件的出现概率。

2.2 谱聚类

谱聚类方法［12～13］可归纳为以下三个主要步骤：1）构建数据集的相似度矩阵W；2）通过相似度矩阵，计算度矩阵和拉普拉斯矩阵的前k 个特征值与特征向量，构建特征向量空间；3）利用k-means 或其它经典聚类算法对特征向量空间中的特征向量进行聚类。假设数据集X 有c 个簇，谱聚类的目标函数：

Y=［y1，y2，y3，…yn］T∈Rn×c是聚类指示矩阵，Y∈Idx表示每个样本的类标签向量，即向量yi∈｛0，1｝c×1只包含一个元素1，其他的元素均为0。由于在Y上施加离散约束会导致NP 难问题，为了解决这个问题，对Y 松弛化，得到连续的聚类指示矩阵F=［f1，f2，f3，…，fn］T∈Rn×c，目标函数转换为

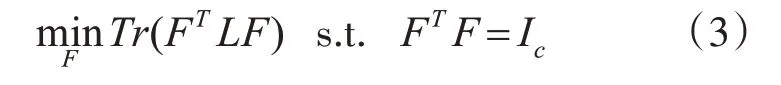
FTF=IC是正交约束，F 的最优解决方法是包含拉普拉斯矩阵L 的c 个最小特征值对应的c 个特征向量。

3 基于多变量自学习与融合策略的多视图聚类算法

3.1 基本思想

本算法相继自学习三种多视图数据的变量，即视图内全局变量、视图内局部变量和视图间变量。为了充分捕获多视图数据的信息，本算法使用信息熵理论来自学习多变量，充分考虑特征与特征、特征与视图和视图与视图的潜在关系。

给定多视图数据X=｛x1，x2，…，xn｝∈Rd×n，其中，d表示每个样例的属性维数，n表示样本个数，X 的第（i，j）项、第i 个样本、第j 个属性分别用xij、xi和xj表示，s表示视图个数，c表示多视图数据的类个数。

视图内全局变量：首先，对于各视图的每个属性，计算所有样本与均值的偏离程度gij，然后，依据偏离程度和聚类个数，得到视图内全局变量中每个项的Gij，其计算公式为

其中，m 是当前视图第j个属性的所有样本的均值，l是该项所在属性的最小偏离值，b是该项所在属性的最大偏离值。

视图内局部变量：根据视图内全局变量和信息熵理论，视图内局部变量中每个属性对应的值可被定义为

果实受到病虫害和鸟类危害之后会严重影响到果实的外部商品性能，还会导致果树出现落果现象，影响到果实质量，从而给养殖户造成更多的额外损失。为了有效预防上述情况发生，在果实形成之后对果实进行套袋处理，能够有效避免上述多种因素损害，同时，还能够保持果实应有的色彩和饱满度。果实套袋时间要结合不同果树品种综合选择，一般情况下，果实套袋时间应该在果实进入膨大期后进行。

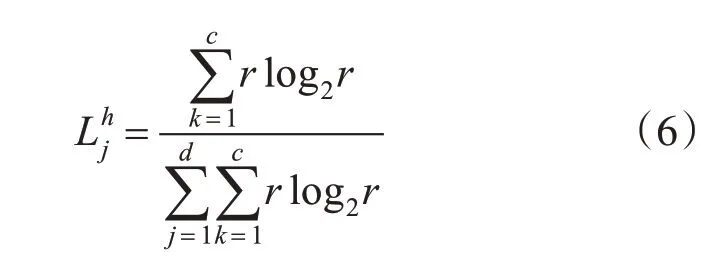
其中，r 是k 在当前属性中出现的总次数占所有样本个数的比值。

视图间变量：基于每个视图的视图内全局变量、视图内局部变量和该视图中属性数目占所有视图属性数目的比例，定义视图间变量中每个视图对应的值，如下所示：

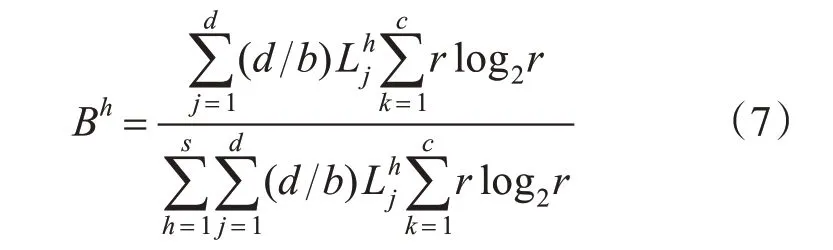
其中，b为所有视图特征的总个数。

融合：相似性度量函数计算公式如下：

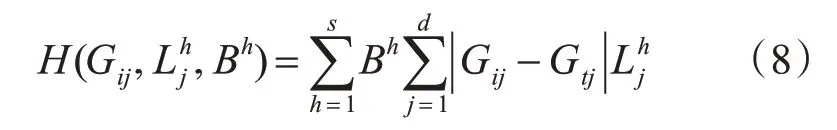
通过式（8），可得到多视图数据的融合矩阵。在此基础上，构建邻接矩阵W。首先，使用K 近邻方法计算中间矩阵P，其基本思想是，若样本点i属于样本点j 的k 近邻样本或样本点j 属于样本点i 的k 近邻样本，则对应的P 矩阵项设为1，否则，为0，公式为

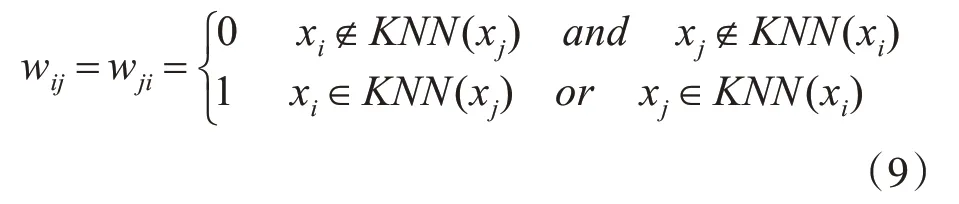
其中，KNN（xi）表示样本xi的k 个近邻样本。然后，由中间矩阵P形成最终邻接矩阵W，其计算公式为

3.2 算法描述

基于多变量自学习与融合策略的多视图聚类算法首先根据聚类数目，通过式（4）和式（5）获取每个视图的视图内全局变量；基于视图内全局变量和信息熵理论，使用式（6）计算每个视图的视图内局部变量；在此前计算的基础上，利用式（7）获取视图间变量。其次，相似性度量函数将基于数据集自学习的多个变量融合为一个矩阵。之后，运用式（9）、式（10）、式（11）相继计算邻接矩阵、度矩阵和拉普拉斯矩阵。通过k-means 获得最终的聚类结果。具体步骤如下：

本文的算法内容主要包括两个部分，第一部分是多变量自学习与融合，第二部分为获取聚类标签过程。多变量自学习与融合的时间复杂度为O（n2），获取聚类标签过程的时间复杂度为O（n2），算法的整体时间复杂度为O（n2）。

4 实验分析

在1 台Intel（R）Core（TM）i5-8250U CPU @1.60GHz 笔记本电脑，Windows 10 操作系统中使用Python语言在Anaconda2的Spyder4.1.5平台实现了基于多变量自学习与融合策略的多视图聚类算法。

4.1 实验设置

本实验采用5 个数据集评估提出的MSFC 算法，包括Handwritten（手写数字0～9 的多视图数据集，共6 个视图）、Anuran Calls（青蛙音节的特征数据集，共两个视图）、IS（室外图像数据集，共两个视图）、Cloud（AVHRR 图像数据集，共两个视图）、3sources（多视图文本数据集，共3 个视图）。将所提算法与6 个多视图聚类算法进行比较，包括AASC［14］（亲和性聚合谱聚类算法）、RMSC［15］（通过低秩和稀疏分解实现的鲁棒多视图谱聚类算法）、MVGL［16］（图学习的多视图聚类算法）、AWP［17］（通过自适应加权普氏分析的多视图聚类算法）、WMSC［18］（基于谱扰动的加权多视图谱聚类）、MCGC［19］（多视图共识图聚类算法）。为了有效评估各个聚类算法的性能，本实验使用四种指标作为评估度量，包含ACC（准确率）、ARI（调整兰德系数）、NMI（标准化互信息）和Purity（纯度）。

对于多视图对比算法，我们按照作者原文中给的参数设定分别运行，并选取参数范围内对应的最佳聚类结果作为实验的最终结果。在所有对比算法的实验中，我们将最近邻的数目kNN 均设置为6。对于带有参数的算法：WMSC（两个参数）、RMSC（1 个参数）、MCGC（1 个参数），这些算法的参数取值范围为｛10-5，10-4，10-3，…，104，105｝m，其中，m为算法参数的数目。

4.2 实验结果与分析

在本节中，在五个数据集上进行实验来验证基于多变量自学习与融合策略的多视图聚类算法的有效性。表1、表2、表3 和表4 分别展示了四个评价指标的实验结果。

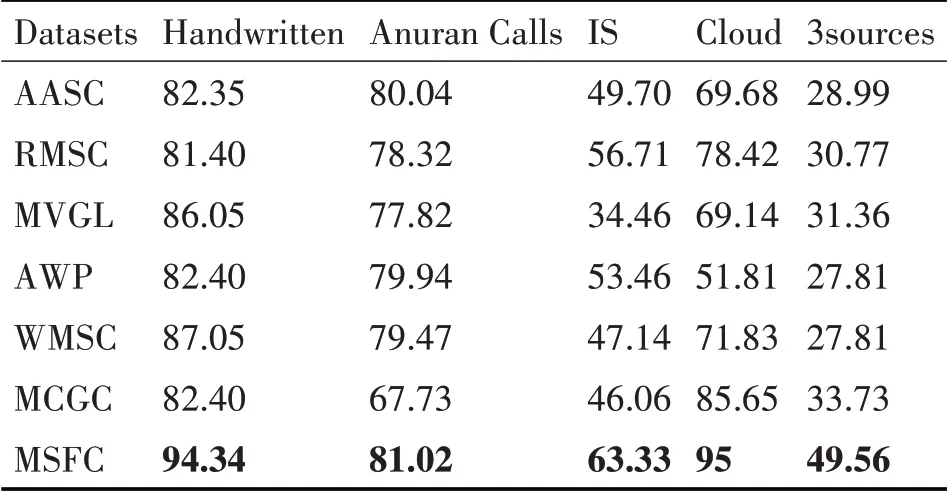
表1 在各个数据集上的ACC实验结果（%）；每列的最高分数用黑体标出

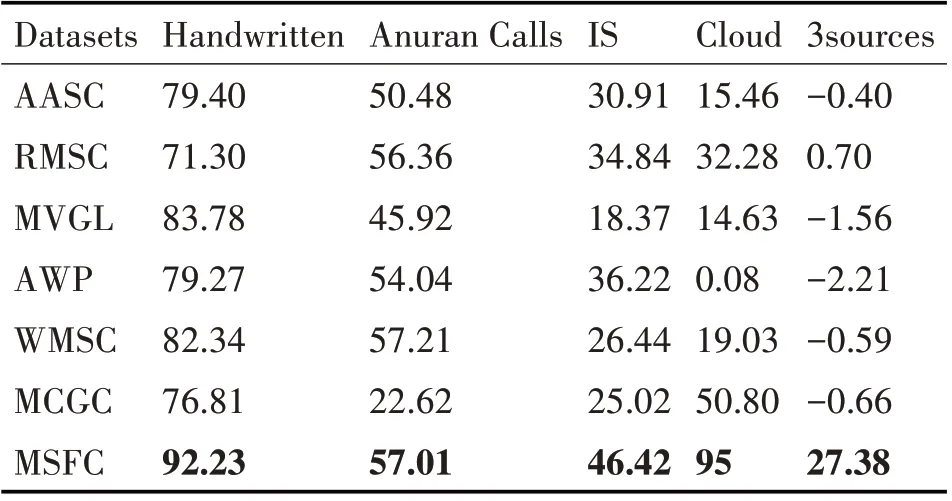
表2 在各个数据集上的ARI实验结果（%）；每列的最高分数用黑体标出

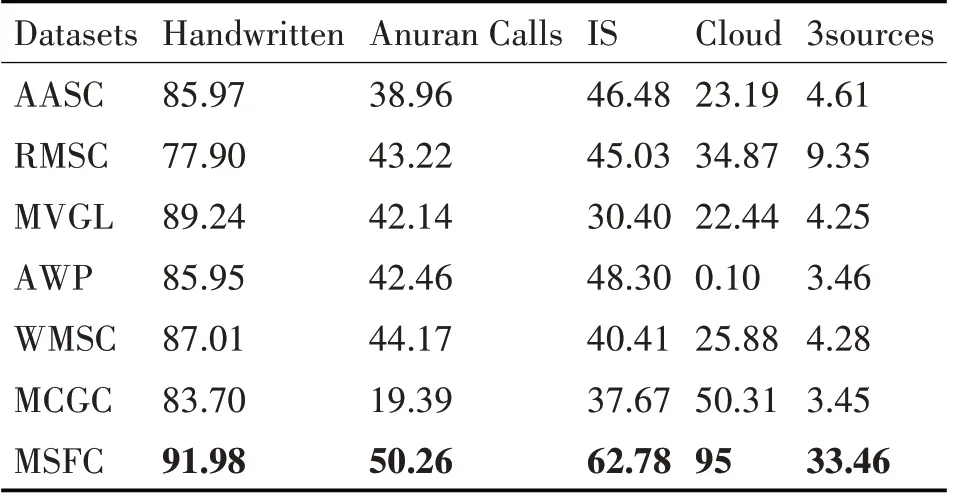
表3 在各个数据集上的NMI实验结果（%）；每列的最高分数用黑体标出

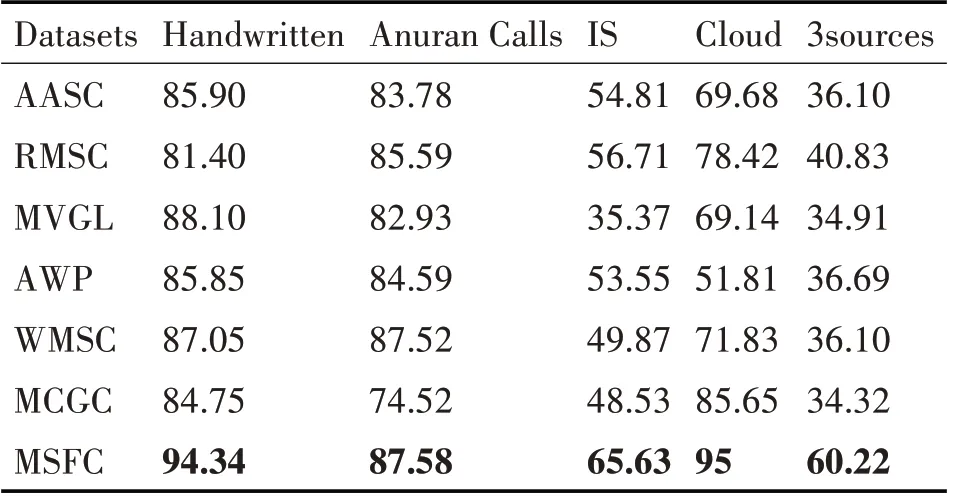
表4 在各个数据集上的Purity实验结果（%）；每列的最高分数用黑体标出

从总体上来看，本章提出的基于多变量自学习与融合策略的多视图聚类算法在多个多视图数据集上均明显优于所有的多视图聚类基线方法（AASC，RMSC，MVGL，AWP，WMSC，MCGC）。相较于对比方法，MSFC 算法的优势主要体现在以下两个方面。一方面，多变量自学习合理提取了多视图数据的潜在结构信息；另一方面，所提相似性度量函数有效度量了样本之间的相似性关系，从而提升了聚类结果。

5 结语

本文提出了一种基于多变量自学习与融合策略的多视图聚类算法，该算法通过聚类数目和信息熵，对多视图数据的三种变量进行自学习，以充分利用视图内与视图间的潜在信息。在此基础上，构建了一个新的相似性度量函数，进行多变量的融合。在多个数据集上的实验结果表明，本文提出的MSFC 算法优于现有的多视图聚类算法，验证了该算法的可行性和优越性。本文下一步的研究方向为考虑如何能提高算法的运行速度，加快完成多视图数据样本分组的任务。