基于Mogi-Coulomb强度准则的竖井井壁压力计算
2022-07-30关晓迪何盛东魏欢欢朱勇锋
关晓迪 何盛东 魏欢欢 马 迪 朱勇锋
(1.西安理工大学 土木建筑工程学院,陕西 西安 710048;2.郑州航空工业管理学院 土木建筑学院,河南 郑州 450046;3.杨凌职业技术学院 建筑工程学院,陕西 咸阳 712100;4.西安交通工程学院 土木工程学院,陕西 西安 710300;5.长安大学 地质工程与测绘学院,陕西 西安 710048)
0 引 言
长期以来,竖井结构被简化为平面问题,大多采用半经验的方法来进行相关设计[1-4];然而竖井结构往往具有空间效应,其围岩土压力是支护设计中研究多年而未能得到很好解决的问题之一。运用能合理反映岩土力学性状的强度准则,可以充分发挥岩土材料的强度潜能,将给竖井等井巷工程建设带来巨大的经济效益[5]。
现阶段,许多相关专家学者对竖井围岩土压力的计算理论开展了较为深入的研究。李造鼎[6]在极限平衡理论的基础上,假定井帮周围土体沿柱状面垂直下滑,推导出了竖井井壁土压力的解析表达式。林小松[7]针对建井工程中井壁面上所受荷载沿深度成多项式变化的特点,推导出了柱面上承受沿深度线性变化的正压力的单层、两层及多层有限长厚壁圆筒应力场。周国庆等[8]通过分析基于空间弹塑性理论对承受地压、附加力及自重的竖井井壁应力,推导出了竖井井壁土压力计算公式。赵彭年[9]以空间轴对称圆形竖井为研究对象,基于哈尔-卡门完全塑性准则,推导出轴对称竖井井壁的主动土压力解析解。刘孟彬等[10]根据竖井设计基本理论,推导出了黄土区竖井井壁土压力计算公式。Zheng Rongming[11]通过引入广义环向压应力系数来修正哈尔-卡门完全塑性假定,推导出了竖井衬砌主动土压力简化滑移线解。周杨等[12]应用双重级数法,推导出了满足所有侧面及端部应力边界条件的弹性解,计算出了某竖井约束内壁治理前后的应力分布。应宏伟等[13]通过建立正交挡墙三维有限元分析模型,推导出了竖井挡墙的主动土压力计算公式。上述研究成果均有益地推进了竖井围岩土压力计算理论的发展和完善。
值得注意的是,据了解,截至目前,针对竖井围岩空间主动土压力方面的研究较少,远滞后于工程实际需要[14]。为此,笔者基于 Mogi-Coulomb强度准则,对轴对称竖井围岩主动极限平衡状态开展分析,推导出井壁结构主动土压力新解,并将所得结果进行比较验证,探讨了中间主应力系数对井壁结构主动土压力分布规律的影响。
1 Mogi-Coulomb强度准则
Mogi[15-16]在多种岩土真三轴试验数据的基础上,提出了Mogi经验强度准则,其通式为

式中:τoct为八面体剪应力;f为单调递增函数;σ13为平均主应力;σ1、σ2、σ3分别为最大主应力、中间主应力和最小主应力。
Al-Ajmi等[17]将Mogi经验强度准则和Coulomb强度准则相结合,建立了Mogi-Coulomb强度准则,其表达式为
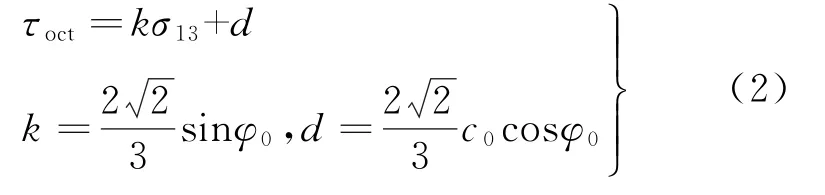
式中:φ0 为岩土的内摩擦角;c0为岩土的黏聚力。
由式(2)可见,Mogi-Coulomb强度准则考虑了中间主应力σ2对岩土强度的影响。工程实践中,常用中间主应力系数b来表示中间主应力与最大、最小主应力的函数关系[18],其表达式为

将式(3)代入式(2),得到Mogi-Coulomb强度准则的主应力表达式:

当中间主应力系数b=0或1时,式(4)退化为Mohr-Coulomb强度准则的主应力表示式,即
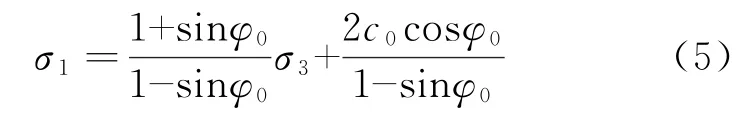
可见,Mohr-Coulomb 强度准则为Mogi-Coulomb强度准则的特例,对应的中间主应力系数b=0或1。
针对轴对称竖井围岩问题,存在应力分量如下:径向正应力σr、环向正应力σθ、轴向正应力σz和剪应力τrz,且σθ=σ2[19-20]。令
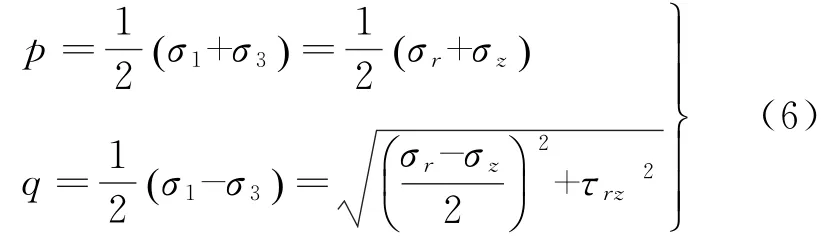
式中:p为平均主应力;q为广义剪应力。
联立式(3)和(6),可得

则轴对称竖井围岩问题的应力分量表达式为
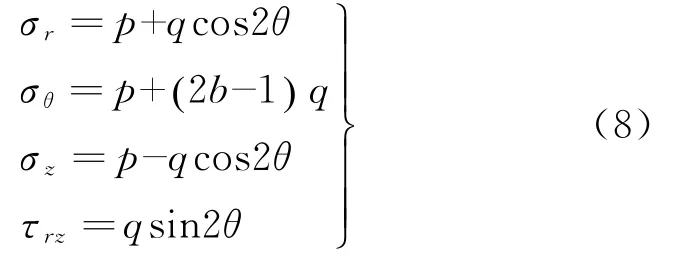
式中:θ为最大主应力σ1与r轴的夹角。联立式(2)和(7),可得

其中,ct、φt分别为
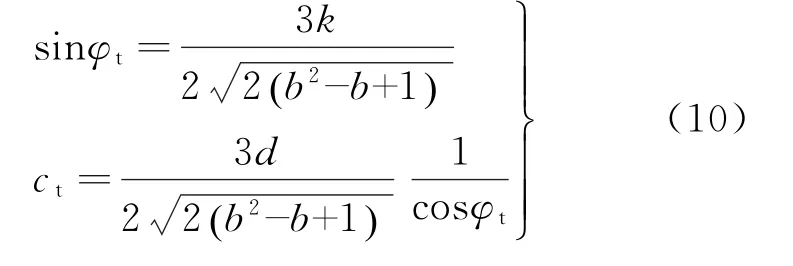
2 井壁结构主动土压力公式推导
图1所示为轴对称竖井围岩任意微元体的受力状态。图中R0为竖井半径,r为竖井围岩任意微元体的半径。轴对称竖井围岩问题的平衡微分方程为
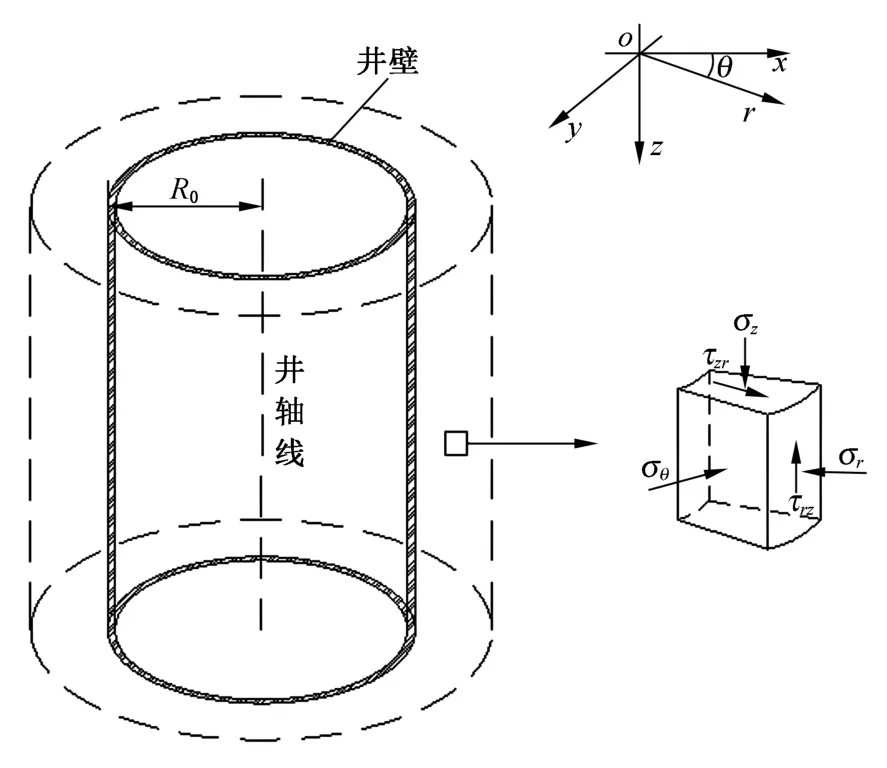
图1 竖井围岩微元体的应力状态

式中:γ为竖井围岩容重。
将竖井围岩的应力分量表达式(8)代入平衡微分方程式(11),可得

若第1族滑移线的弧长用s1表示,第2族滑移线的弧长用s2表示,r-z平面内的井壁围岩的滑移线如图2所示,则式(12)和(13)的特征线方程分别为

图2 r-z 平面内的井壁围岩的滑移线示意
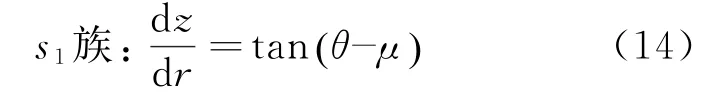

则上述微分方程式(12)和式(13)可转化为体坐标s1和s2的表达式为:

在推导基于Mogi-Coulomb强度准则的竖井围岩空间主动土压力新解过程中,采用空间轴对称问题的统一特征线理论,假定竖井围岩极限状态区被锥形表面圈定,其母线与r轴的夹角为,则在计算竖井围岩空间主动土压力时,可将井壁围岩在r-z平面内的特征线视作2组平行直线,如图3所示。
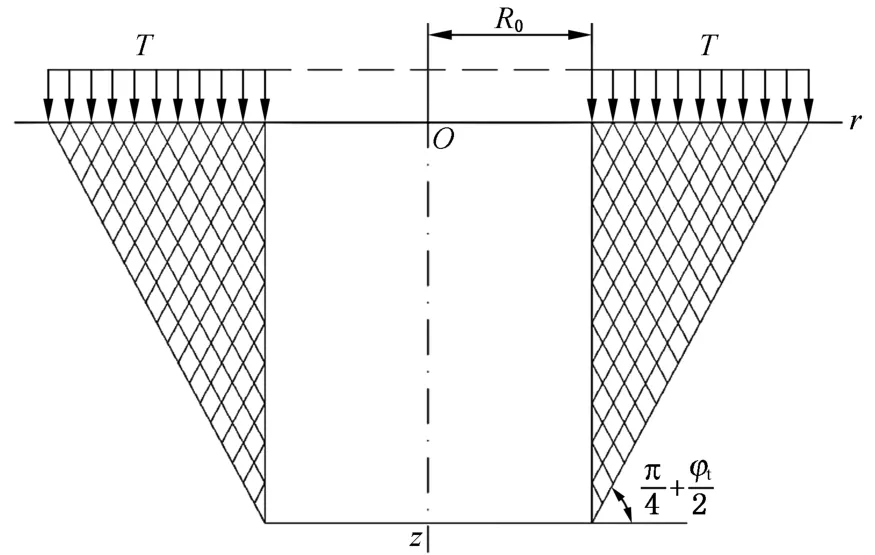
图3 主动极限平衡下的竖井围岩问题计算简图
根据上述假定,则有
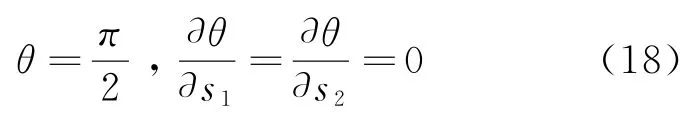
将式(18)代入式(16)和(17),可得

将特征线方程式(14)、(15)代入式(19),可得

将式(9)代入式(21),可得
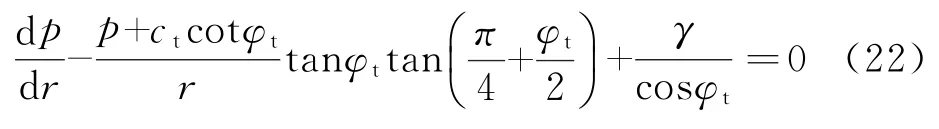
为简化微分方程计算和方便微分形式表达,令

则式(22)可表示为如下形式:
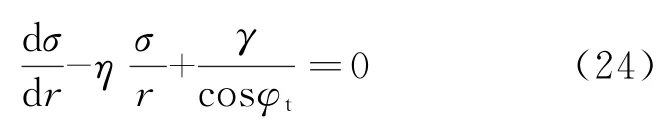
对微分方程式(24)进行求解,得到轴对称竖井围岩在主动极限状态下的应力分量表达式:

式中:C1为积分常数。
若第1族滑移线与井壁交点的纵坐标为za,与水平地表面交点的横坐标为ra,则存在下式:
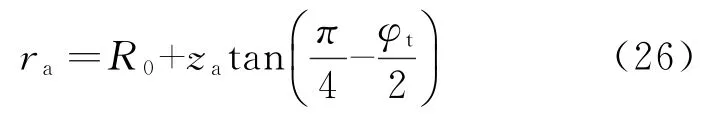

将式(27)代入式(25),可得轴对称竖井围岩在主动极限状态下的应力分量表达式:

令井壁围岩中一点的半径r=R0,将其代入式(28)的第1 式中,可得基于 Mogi-Coulomb强度准则的竖井井壁结构主动土压力新解:

将式(10)、(26)代入式(29),得到基于Mogi-Coulomb强度准则的竖井井壁结构主动土压力pa随着竖井深度za的增加,大致呈幂函数曲线增加的结论;当za→∞时,井壁结构主动土压力趋于常数[9,21],即井壁结构主动土压力为

3 算例分析
为验证推导出的基于Mogi-Coulomb强度准则的竖井井壁结构主动土压力新解的正确性,针对深度z为10 m、半径R0为2 m 的竖井,选取竖井围岩的力学参数如下:黏聚力c0=2 MPa,内摩擦角φ0=20°,容重γ=26×103k N/m3,且表面荷载T=0 k N/m2。
图4所示为竖井深度z=1.0 m 时,不同b值条件下,基于Mogi-Coulomb强度准则的竖井井壁结构主动土压力分布曲线。由图中可知,中间主应力系数b对竖井井壁结构主动土压力值有较大的影响:当0≤b<0.5时,井壁结构主动土压力随着b值的增大而减小;当0.5≤b≤1.0时,井壁结构主动土压力随着b值的增大而增大;且当b=0.5时,主动土压力为最小值。因此,井壁土压力分布曲线呈现出以b=0.5处土压力为对称轴,呈左右对称分布的特点;同时以b=0时的竖井井壁结构主动土压力值(8.57 MPa)作为参照条件,当b=0.1、0.2、0.3、0.4和0.5时,井壁结构主动土压力值分别减小约6.9%、12.9%、17.5%、20.4%和21.4%。
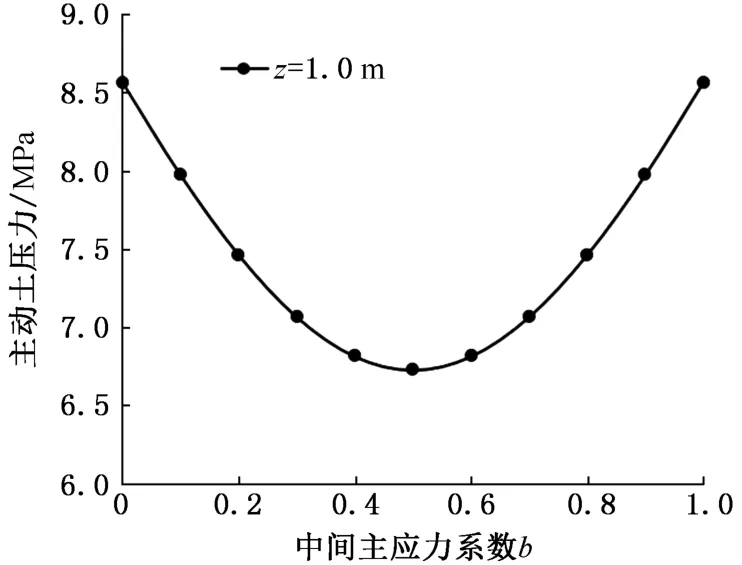
图4 不同b 值对井壁结构主动土压力分布曲线的影响
图5所示为不同b值条件下(由于对称性,选取b=[0,0.5]),基于Mogi-Coulomb强度准则的竖井井壁结构主动土压力随着竖井深度增加的分布曲线。由图中可知,竖井井壁结构主动土压力随着竖井深度的增加,呈幂函数曲线分布;且b值越大,井壁结构主动土压力越小。当b值较小时,随着b值的增大,竖井井壁结构主动土压力的增幅减小。结果表明:基于Mogi-Coulomb强度准则的竖井井壁结构主动土压力值明显小于基于Mohr-Coulomb强度准则(b=0时)的井壁结构主动土压力。这是由于前者在分析井壁土压力时,考虑了中间主应力σ2的影响,使得前者主动土压力值较小。同时基于Mogi-Coulomb强度准则的竖井井壁结构主动土压力值明显小于朗肯主动土压力值。这是由于竖井井壁结构主动土压力具有环形土拱效应,使得竖井井壁结构主动土压力值较小[22]。因此,在工程中,采用基于Mohr-Coulomb强度准则的主动土压力会偏于保守,从而造成井壁支护材料的浪费。

图5 不同b 值条件下的井壁结构主动土压力分布曲线
4 结 论
(1)基于Mogi-Coulomb强度准则,针对轴对称竖井围岩的主动极限平衡状态开展分析,推导出了基于Mogi-Coulomb强度准则的竖井井壁结构主动土压力新解,以期为井壁支护设计提供一定的理论依据。
(2)竖井井壁结构主动土压力随竖井深度的增加,呈幂函数曲线分布;且基于Mogi-Coulomb强度准则的中间主应力系数b对井壁结构主动土压力的影响较大。当0≤b<0.5时,井壁结构主动土压力随着b值的增大而减小;当0.5≤b≤1.0时,井壁结构主动土压力随着b值的增大而增大;且当b=0.5时,主动土压力为最小值。
(3)在工程中,采用基于Mohr-Coulomb强度准则的主动土压力会偏于保守,从而造成井壁支护材料的浪费。引入中间主应力系数b的Mogi-Coulomb强度准则,可更加充分发挥竖井围岩强度潜能,从而可更加经济安全地进行竖井设计与施工。
