改进CEEMDAN算法与分形融合的深度学习轴承故障分析
2022-07-30肖俊青金江涛岳敏楠许子非
肖俊青, 金江涛, 岳敏楠, 李 春,2, 许子非, 孙 康
(1.上海理工大学 能源与动力工程学院,上海 200093;2.上海市动力工程多相流动与传热重点实验室,上海 200093)
21世纪以来,环境保护日益受到重视,目前已列为国家“十四五”规划主要内容,我国将采取必要措施在2030年前达到碳达峰,2060年前实现碳中和,为此必须加强新能源研发力度,促进产业转型[1]。风能、水能以及核能等新能源的发展需要依靠高效稳定的旋转设备,而滚动轴承是旋转设备必不可少的零部件,其运行状况直接影响着整机性能[2]。因此,快速准确地发现轴承故障已成为状态监测和诊断技术分析的主要研究内容。
轴承故障分析虽常用易于大量采集的振动信号,但其复杂的运行环境难以确保信号纯净,且因设备振动和冲击导致信号呈现典型的非线性、非平稳特征,对有效提取特征信息和早期故障预警提出了严峻挑战[3]。而时域分析是诊断领域普遍使用的方法,可有效提取多噪声下非线性信号中的故障信息,可更好地实现机械设备的预防与维护[4]。小波变换(Wavelet Transform, WT)不仅需要分析有、无量纲参数,还需要人工设置分解层数,严重影响了结果的分析精度[5]。经验模态分解(Empirical Mode Decomposition, EMD)方法在信号自适应分解时虽无需人工干预就可保证本征模态函数(Intrinsic Mode Function, IMF)分量良好的完备性,但无法避免模态混叠和端点效应[6];研究者基于传统EMD方法改进提出了集合经验模态分解法(Ensemble Empirical Mode Decomposition, EEMD),在输入信号中添加白噪声可较好地保持数据连续性并抑制模态混叠,但因信号独立性难以分解出相同的数量,并未彻底解决模态混叠的难题[7]。而自适应白噪声总体平均经验模态分解(Complete Ensemble Empirical Mode Decomposition with Adaptive Noise, CEEMDAN)方法可有效避免端点效应,减少冗余和IMF分量中的残余噪声[8]。学者们针对如何准确筛选出有效的IMF分量进行了大量研究,苏文胜等[9]通过IMF分量的峭度与皮尔森相关系数筛选最佳IMF分量;彭畅等[10]使用距离度量因子选择最优IMF分量进行故障分析;蒋超等[11]基于快速谱峭度图挑选敏感IMF分量。以上研究虽取得了一定效果,但均忽略了故障信息不仅存在于单个IMF分量中还可能存在于多个IMF分量中的问题。
大数据时代下,海量、高维数据泛滥,而卷积神经网络(Convolutional Neural Network, CNN)依靠强大的自学习能力广泛应用于故障诊断领域[12]。王丽华等[13]采用短时傅里叶变换对原始数据进行预处理,利用CNN实现了电机故障诊断与分类;雷亚国等[14]利用深度神经网络对机械设备健康状况进行智能诊断,有效挖掘了机械装备大数据中隐藏的信息;Lu等[15]采用重构时间序列输入CNN对滚动轴承进行故障诊断,较好地验证了强噪声下的鲁棒性。以上研究证明CNN善于处理海量、高维数据,且具有强大的自学习能力,但均未考虑噪声对故障诊断的影响。
针对以上不足,笔者采用主成分分析(Principal Component Analysis, PCA)降维与分形盒维数联合方法筛选CEEMDAN算法分解的有效IMF分量并重构,克服了现有研究选取最佳单一IMF分量的不足,并依靠强大自学习能力的CNN对隐含故障信息进行进一步挖掘。通过添加不同信噪比还原实际噪声分析对故障诊断的影响,以验证所提方法的鲁棒性与泛化性。
1 改进CEEMDAN算法
1.1 CEEMDAN算法
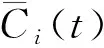
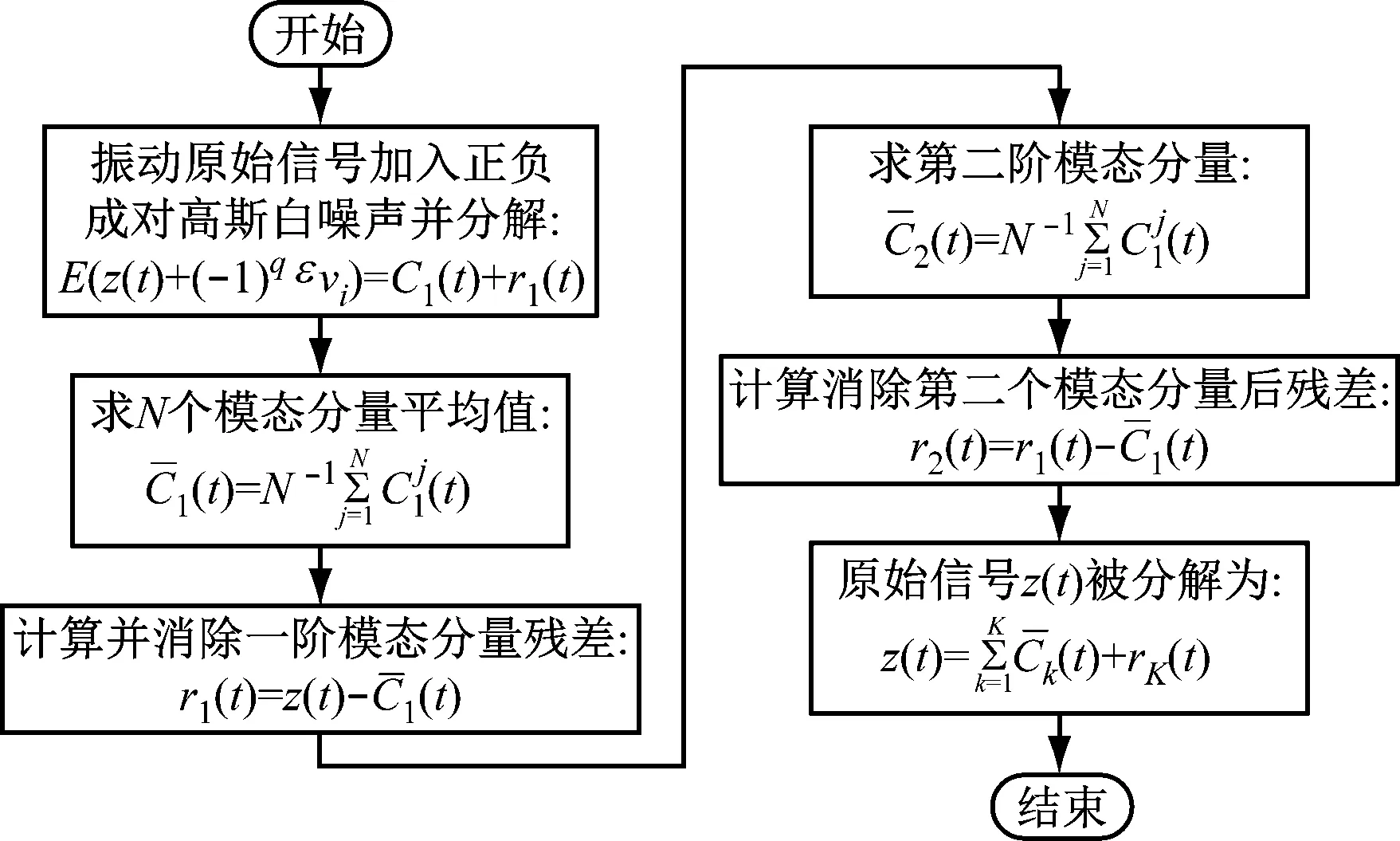
图1 CEEMDAN算法流程图Fig.1 Flow chart of CEEMDAN algorithm
1.2 分形与主元分析
因分形可以较好地分析部分与整体的自相似性、反馈体系无标度性及定量分析,因此深受非线性领域研究者的青睐[17]。而主元分析可对高维、海量数据进行降维处理并提取主要特征信息,简化计算的同时提升效率[18]。
1.3 改进CEEMDAN算法
自适应添加白噪声的CEEMDAN算法,虽有效降低了模态混叠问题,但仍无法彻底消除冗余分量和虚假分量的影响,干扰主分量筛选。而大部分学者采用皮尔森相关系数、峭度以及灰色关联度等方法筛选最优IMF分量[19],忽略了故障信息往往存在于部分IMF分量中,导致有效信息难以完全提取。笔者采用PCA与分形盒维数结合的方法改进CEEMDAN算法,PCA可对数据降维以提取有效故障信息,采用交叉分析法计算降维前后的分形盒维数确定最佳分量组,分形盒维数越大,表明信号越混乱,反之,则信号越稳定。改进的CEEMDAN算法流程图如图2所示。其中,p为最佳IMF分量的个数。
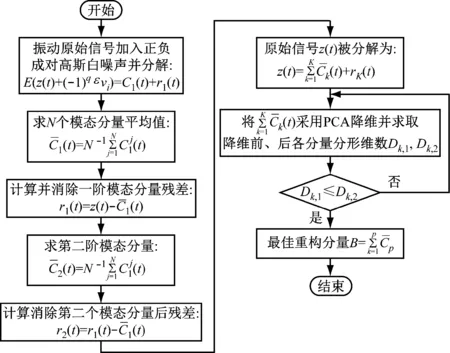
图2 改进CEEMDAN算法流程图Fig.2 Flow chart of improved CEEMDAN algorithm
2 卷积神经网络
卷积神经网络源于灵长动物视觉神经系统神经元,不仅具有深层结构的神经网络,还有强大的数据挖掘与特征提取能力[20]。而局部感受野、权值共享及下采样作为其独有特征,不仅可实现数据特征的深度挖掘,还可增强数据特征的自学习能力,较好地消除算法过拟合[21]。CNN模型结构如图3所示。
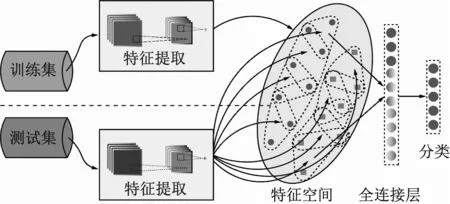
图3 卷积神经网络模型结构Fig.3 Model structure of CNN
2.1 卷积、池化层
卷积层作为CNN的核心,利用卷积核与输入特征重合区域对应乘积并重构,经添加偏置以获取特征值实现特征信息提取。数据经卷积层虽提高了特征信息提取能力,但增加了数据维度,易造成维数灾难,而池化层可在保留其关键特征的同时减少参数量,实现降维和筛选主要特征的目的[22]。其数学表达式为:
pj=f(yi+bj)
(1)
pk=f(βj·ϑ+bj)
(2)
式中:pj为卷积输出;pk为池化输出;yi为输入数据;bj为偏置;βj为网络偏置;ϑ为子采样函数;f(·)为激活函数(Relu);i,j,k∈R。
2.2 全连接层与Dropout
全连接层可对特征信息进行有效分类,其包含的多层感知机隐含层可较好整合卷积、池化后的数据信息[23]。Dropout正则化技术[24]可将隐藏层的部分单元忽略以防止过拟合现象,提高模型的泛化性能,Dropout效果示意图如图4所示。
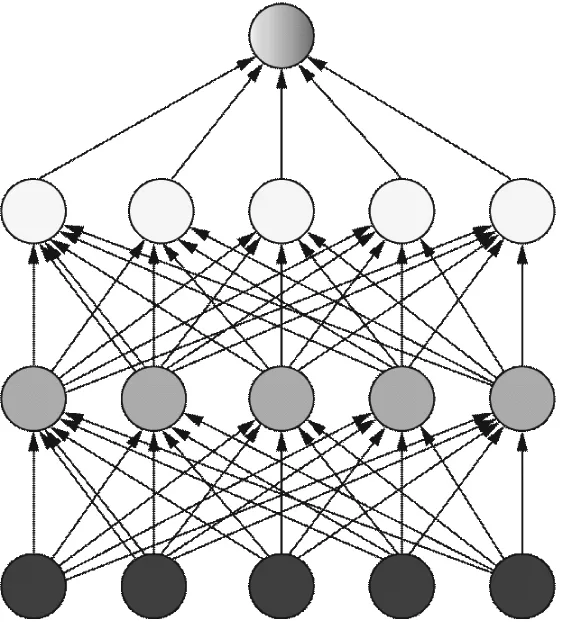
(a) 标准的全连接网络
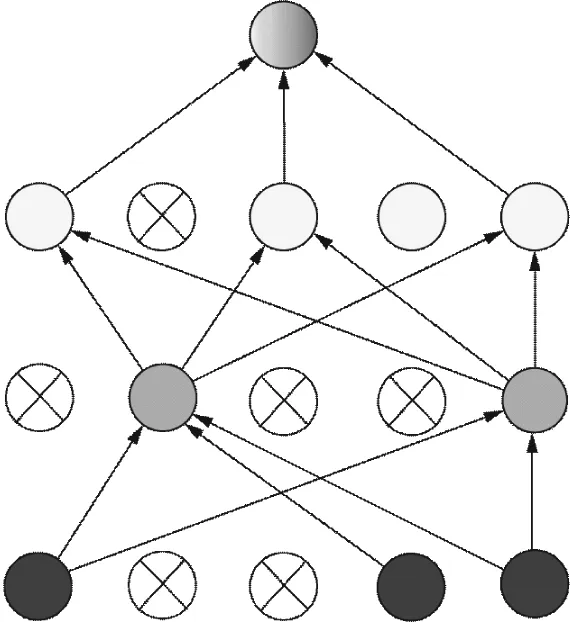
(b) Dropout后的网络图4 Dropout效果示意图Fig.4 Effect schematic diagram of Dropout
3 故障诊断模型
CEEMDAN可有效避免端点效应,减少冗余和IMF分量中的残余噪声;PCA可将难于识别的故障映射到另一子空间进行降维处理以提取关键特征信息;分形盒维数作为最佳重构分量筛选条件,可进一步剔除IMF冗余分量及虚假分量;而CNN依靠强大的数据处理优势,对其故障信息进行准确识别与分类。模型结构如图5所示。
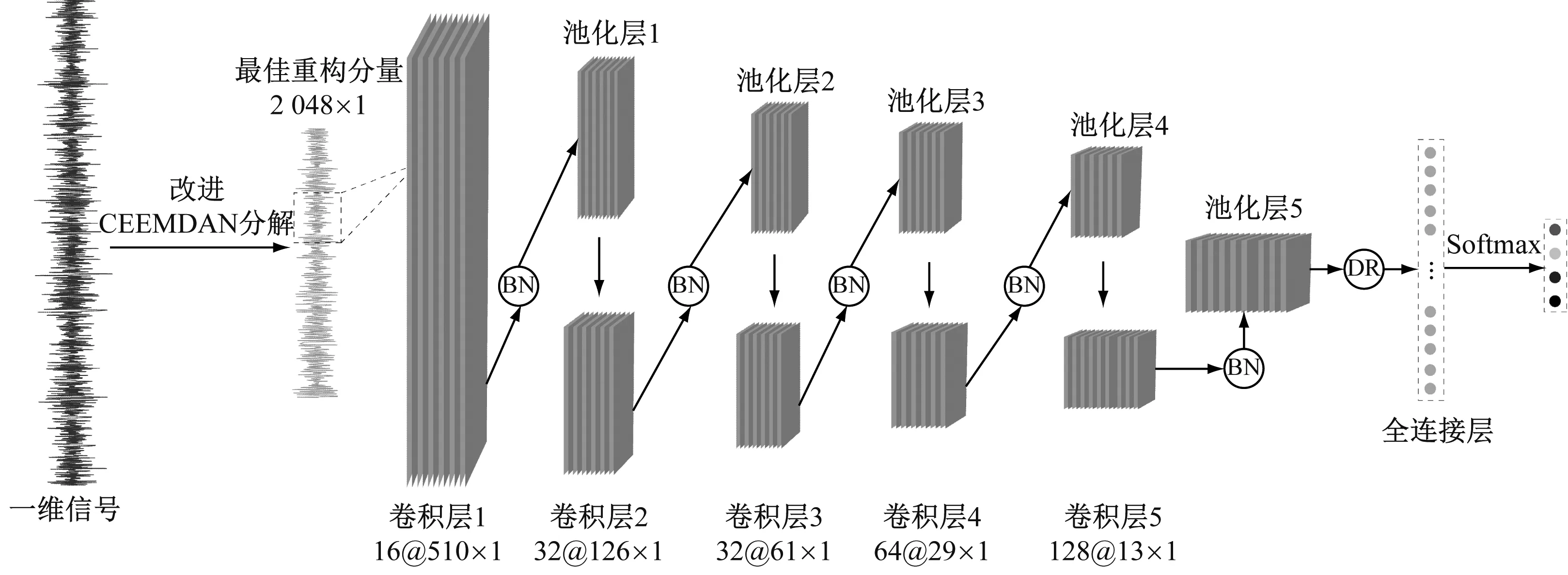
图5 改进CEEMDAN融合CNN模型结构图Fig.5 Structural diagram of improved CEEMDAN fusion CNN
由图5可知,通过改进CEEMDAN分解获取4种故障信号各最佳重构分量,将其导入含5层卷积层、5层池化层、5层Batch Normalization (BN)层和1层Dropout (DR)层和1层全连接层的CNN中,由Softmax进行故障识别与分类。采用BN、DR不仅可简化计算、提高故障识别率,还能有效避免梯度爆炸、过拟合以及梯度消失等现象。
针对单一CEEMDAN和CNN算法存在的不足,笔者提出了一种改进CEEMDAN融合CNN的故障诊断方法,诊断流程如图6所示。
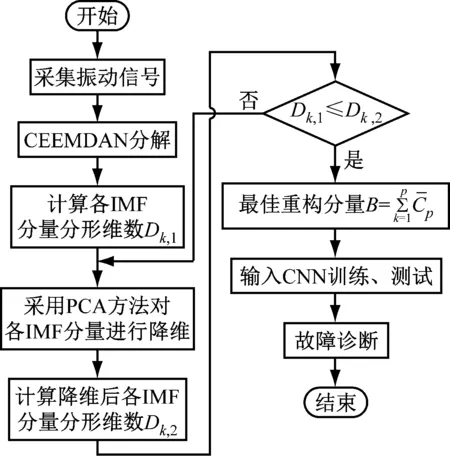
图6 故障诊断流程图Fig.6 Flow chart of fault diagnosis
4 试验验证
4.1 试验参数
为较好地评估实际情况,采用西安交通大学公开的轴承振动数据[25]验证本文故障诊断方法的优越性。轴承试验测试平台如图7所示。

图7 轴承测试平台Fig.7 Test platform of the bearing
试验平台电机转速为2 100 r/min和2 250 r/min,采样频率为25.6 kHz。试验工况如表1所示。由表1可知,轴承存在混合损伤、内圈磨损、保持架磨损及外圈磨损4种故障,其时域、频域图如图8所示,其中f为频率。
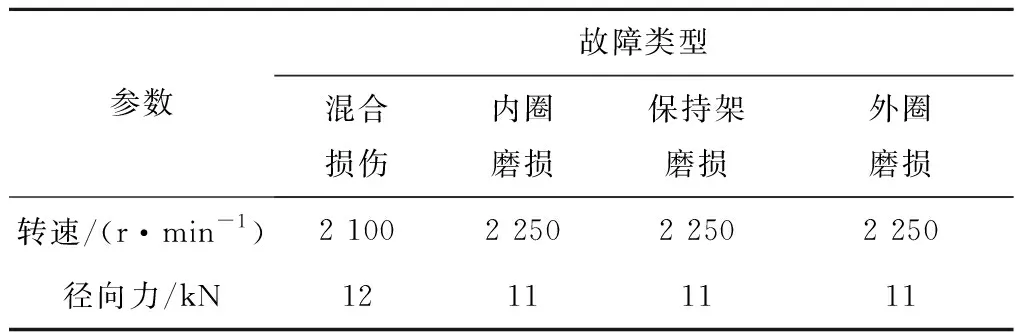
表1 轴承试验工况Tab.1 Test conditions of the bearing
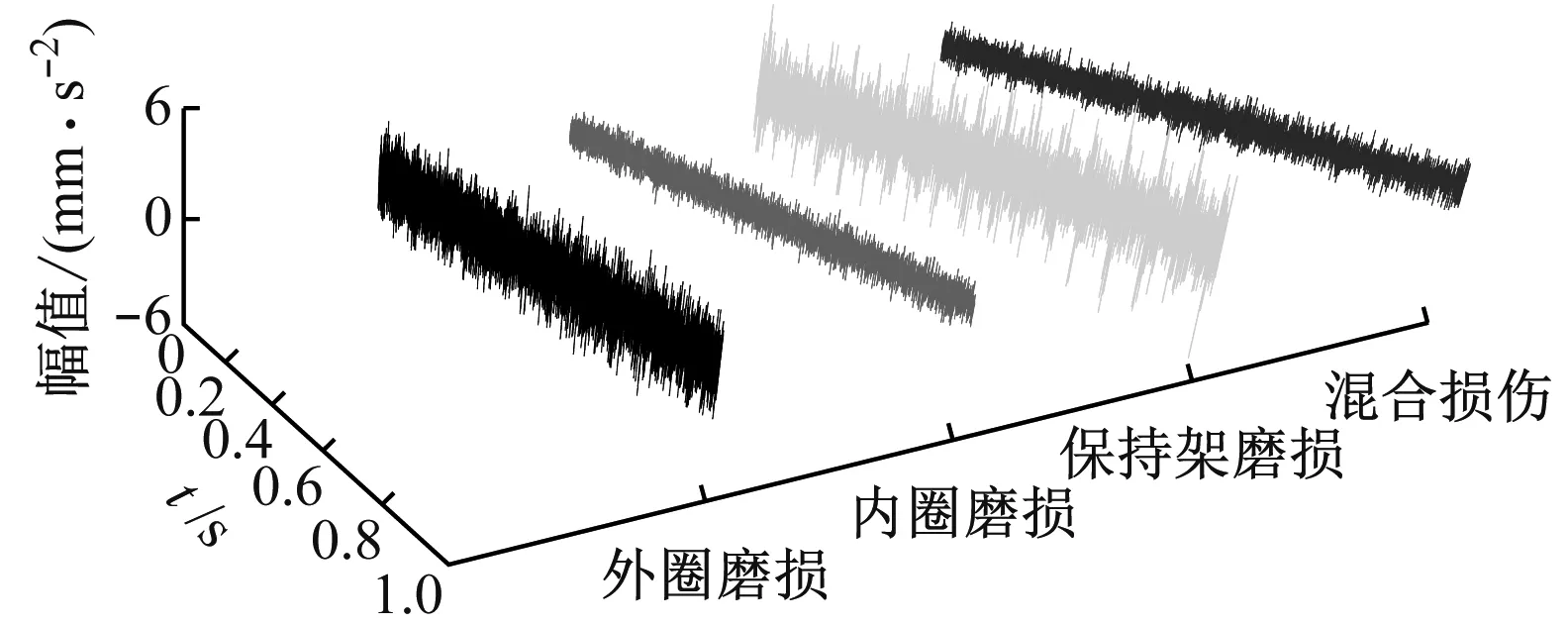
(a) 时域波形
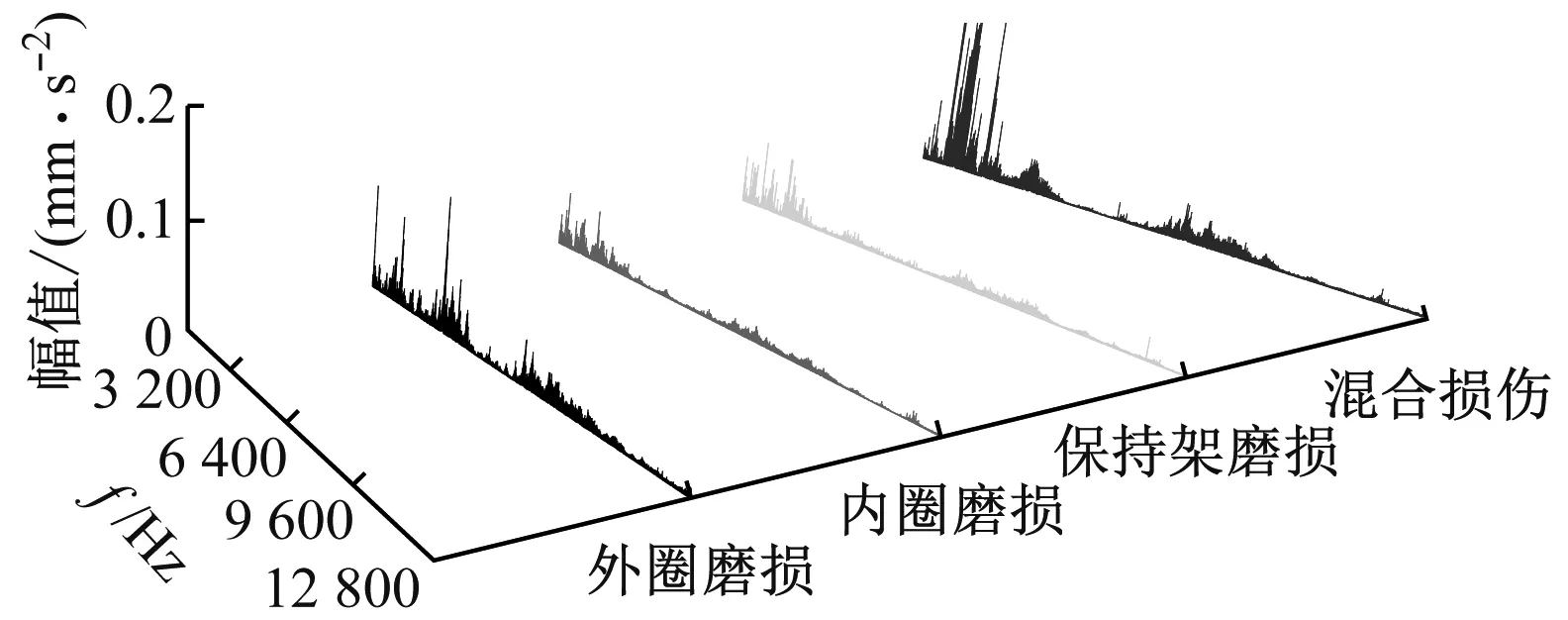
(b) 频域波形图8 轴承振动信号时域和频域波形Fig.8 Time and frequency domain waveform of the bearing vibration signals
由图8可知,滚动轴承不同故障振动信号时域和频域图整体虽有一定差异,但无法直接进行故障识别与分类,更难保证其诊断精度。而提取准确、纯净及有效的故障特征才是诊断的基础,因此需对原始信号进行降噪处理以突显故障信息,增强信号的实用性。
4.2 数据预处理与方法分析
将原始信号分别采用EMD、EEMD以及CEEMDAN 算法实现降噪处理,但因数据过多且无法直接进行诊断,因此仅展示内圈磨损分解结果,如图9所示。
由图9可知,从3种算法的时域和频域图无法准确筛选最佳重构分量进行故障分析,与EMD、EEMD算法相比,CEEMDAN算法虽采用自适应添加白噪声改善模态混叠的影响,但仍无法准确剔除冗余分量和虚假分量。
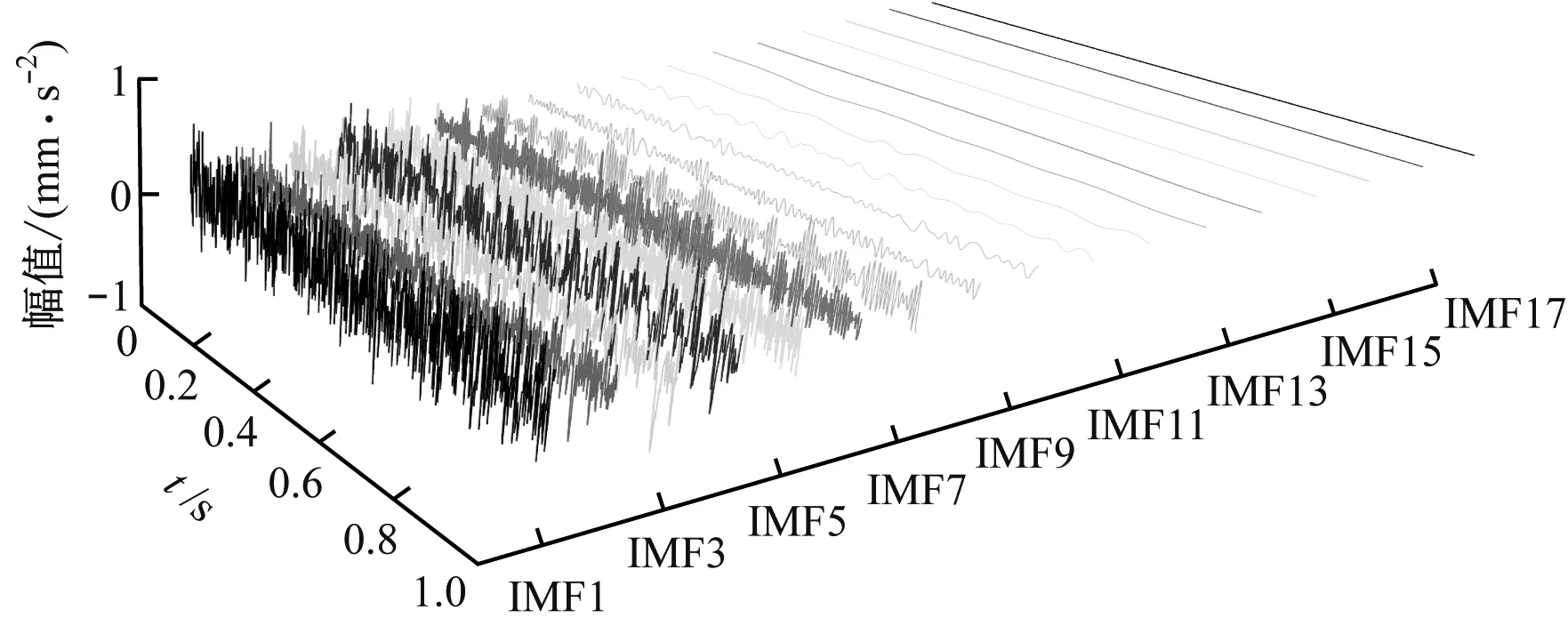
(a) EMD分解结果
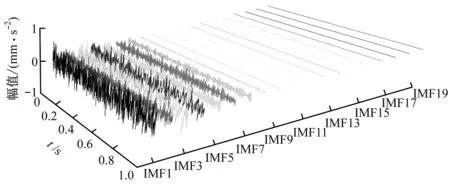
(b) EEMD分解结果
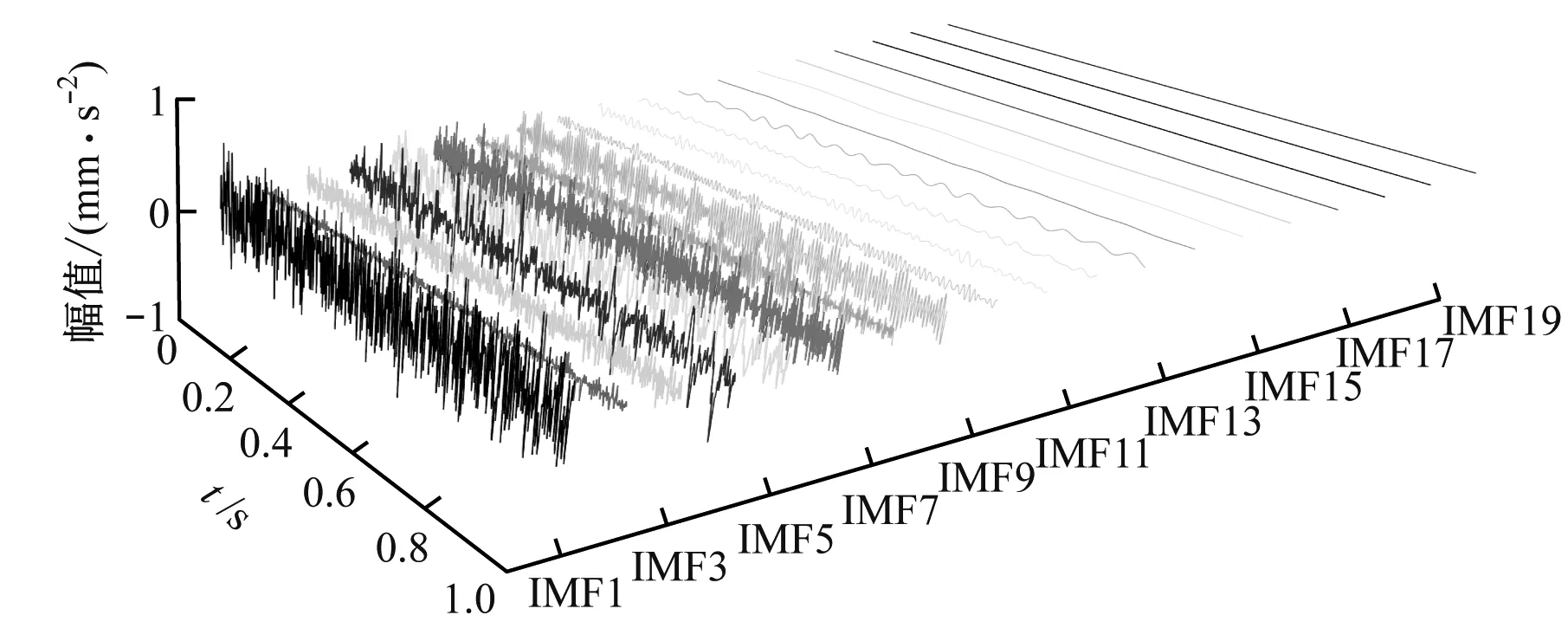
(c) CEEMDAN分解结果图9 内圈故障信号分解结果Fig.9 Decomposition results of inner ring fault signal
基于以上问题,采用PCA降维与分形盒维数结合的方法筛选最佳重构分量,4种故障降维前后的分形盒维数对比结果如图10所示。
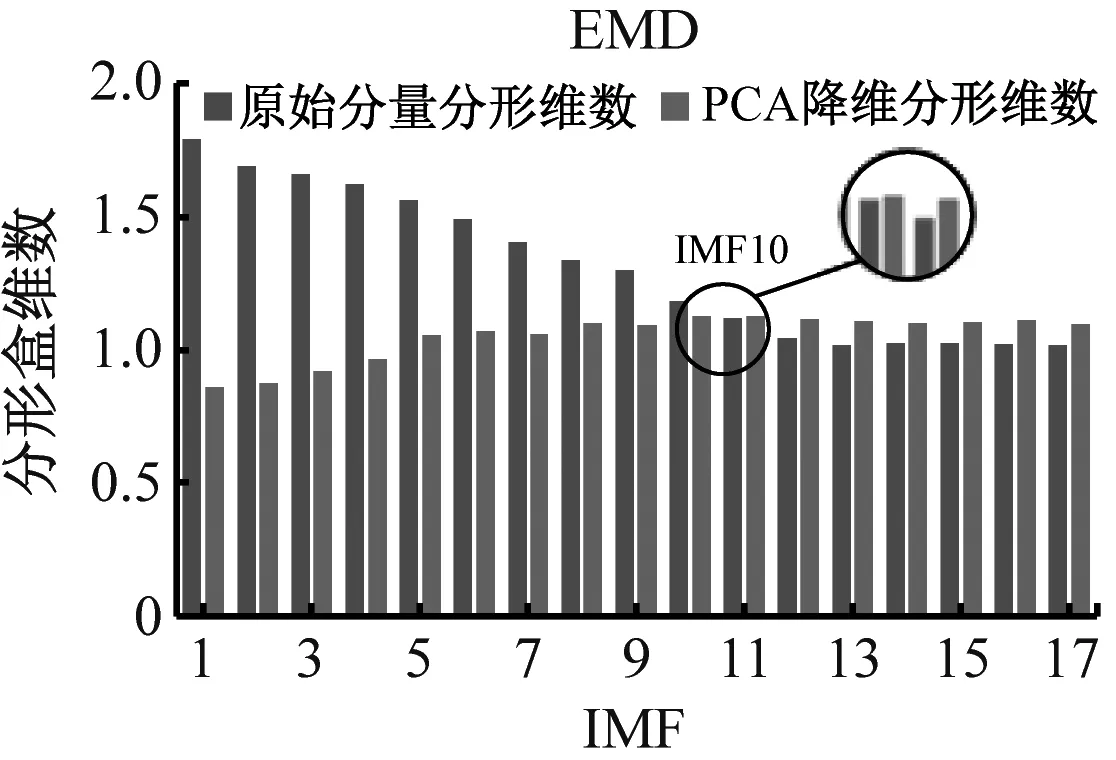
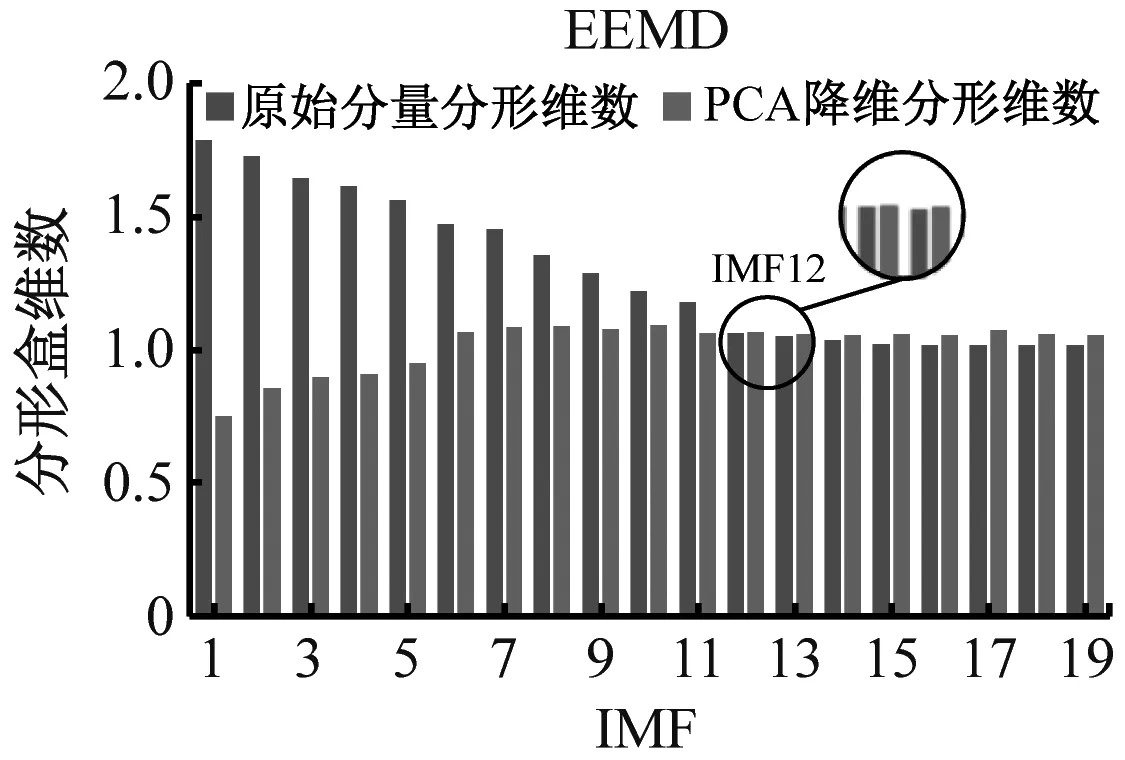
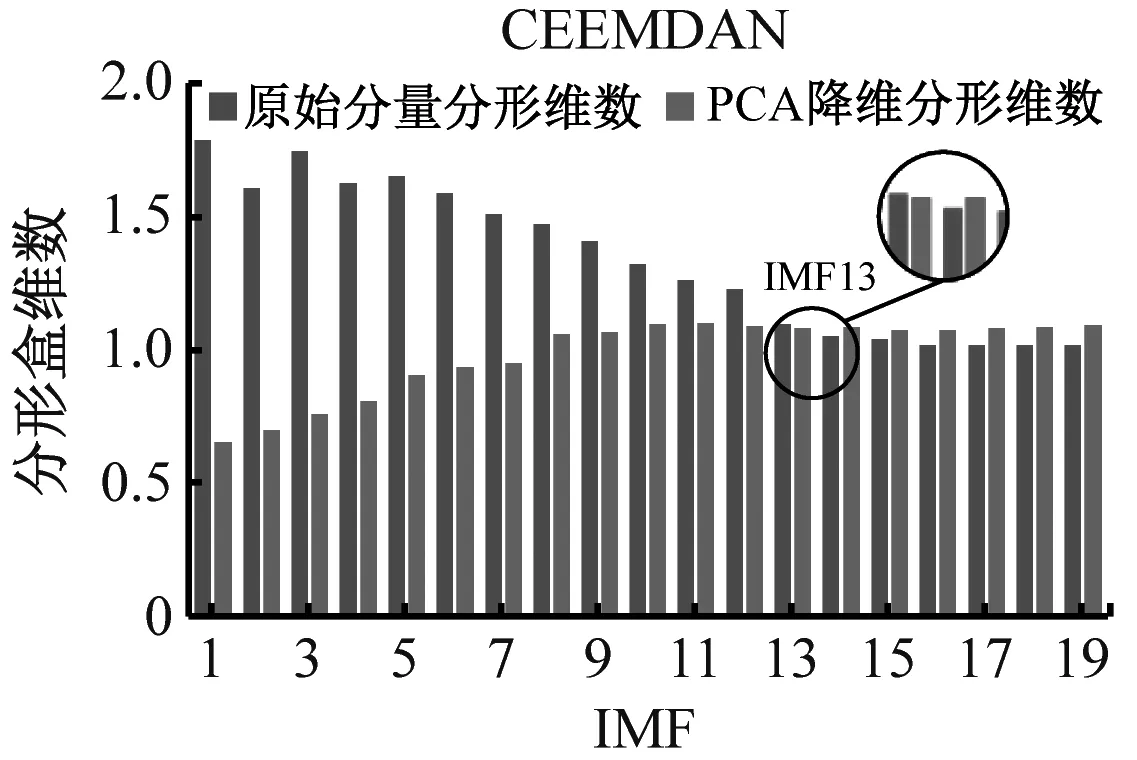
(a) 内圈磨损
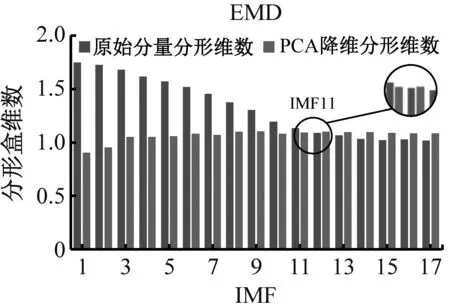
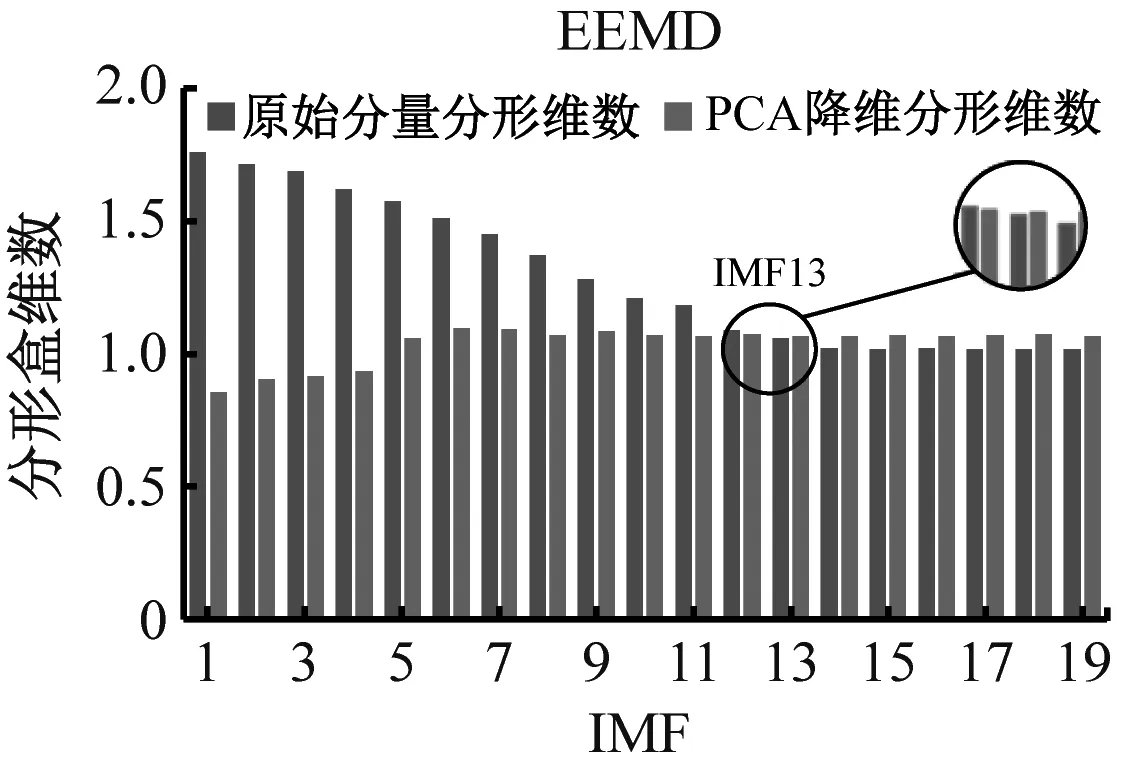
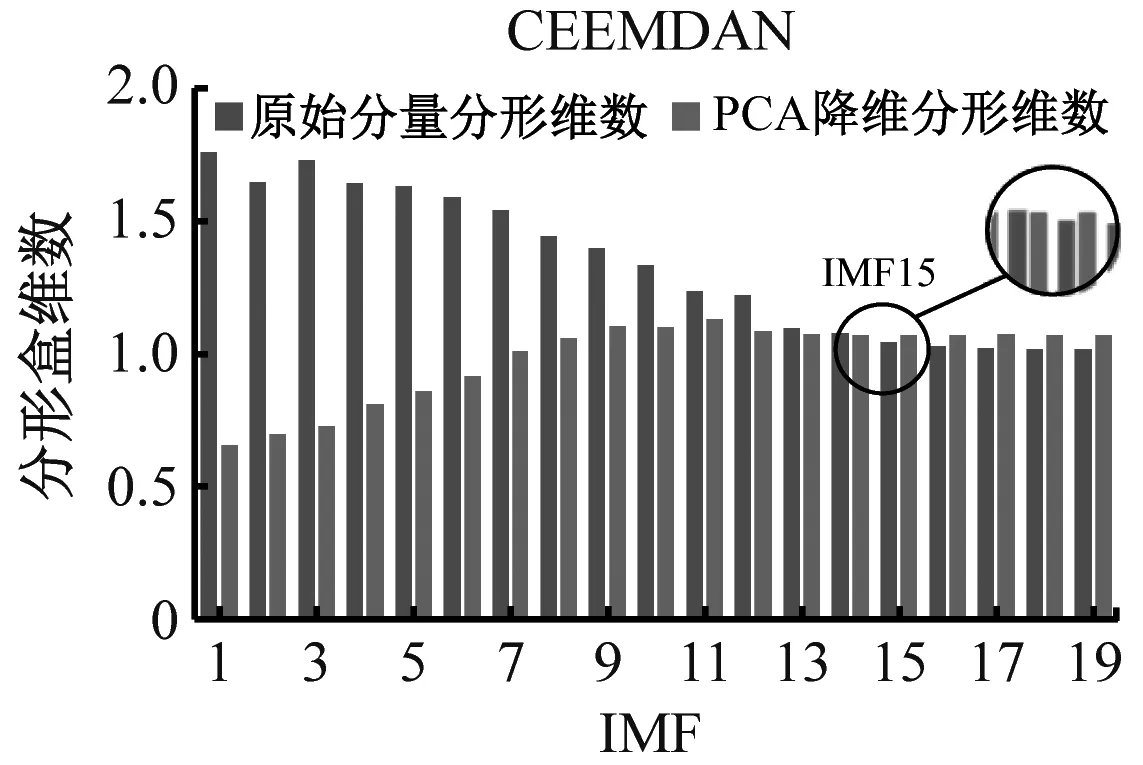
(b) 外圈磨损
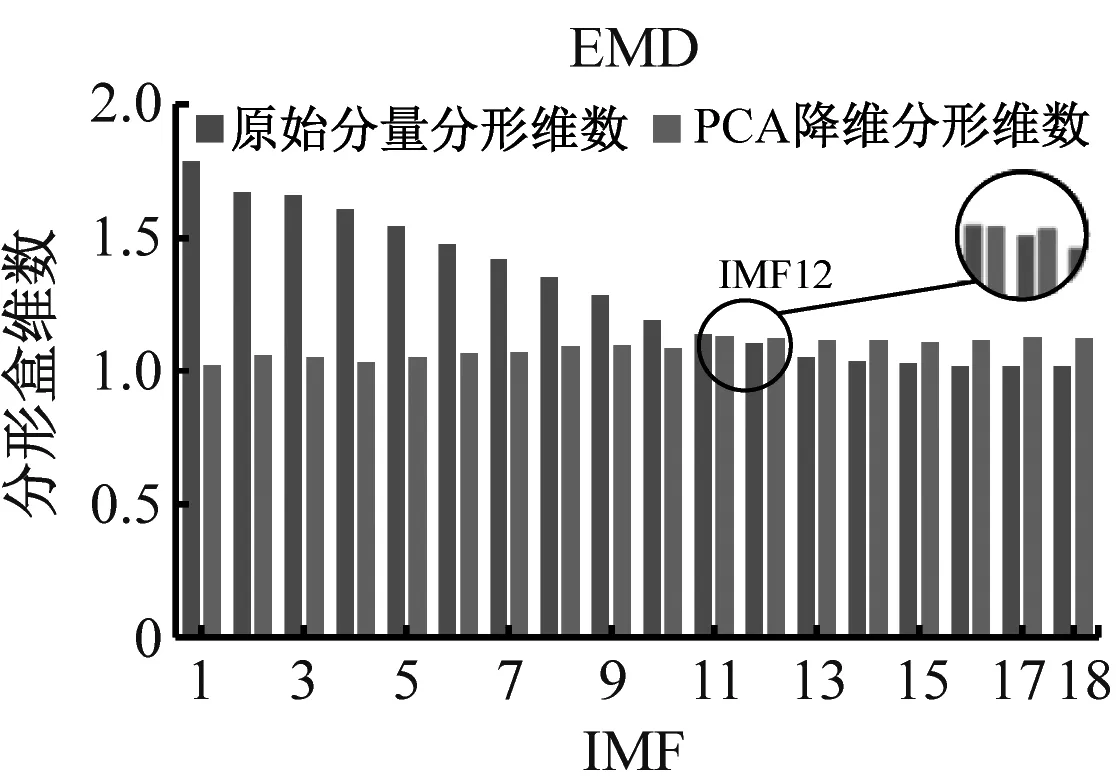
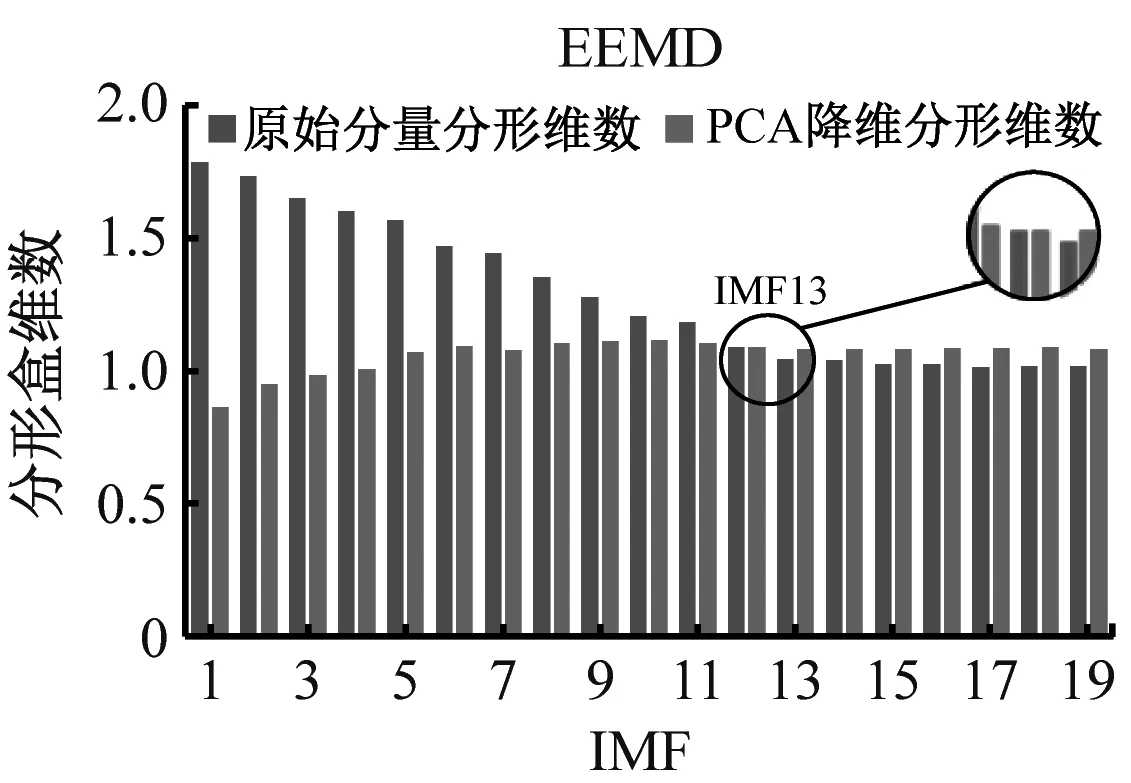
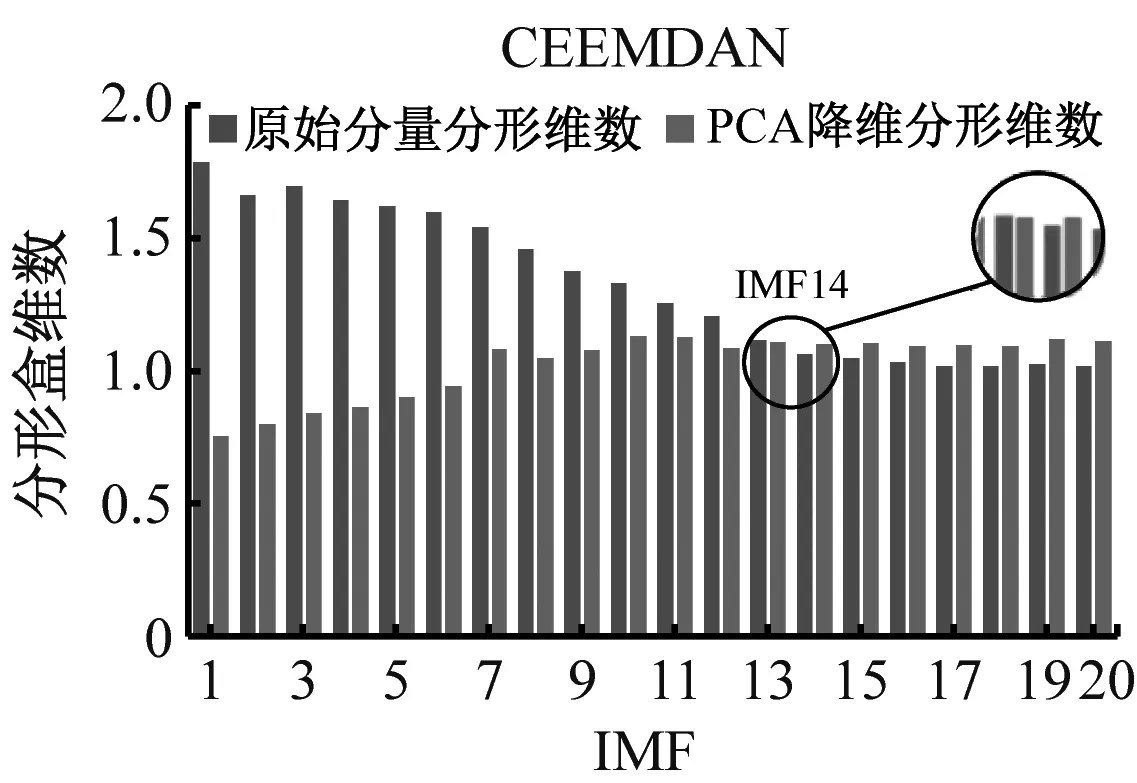
(c) 混合损伤
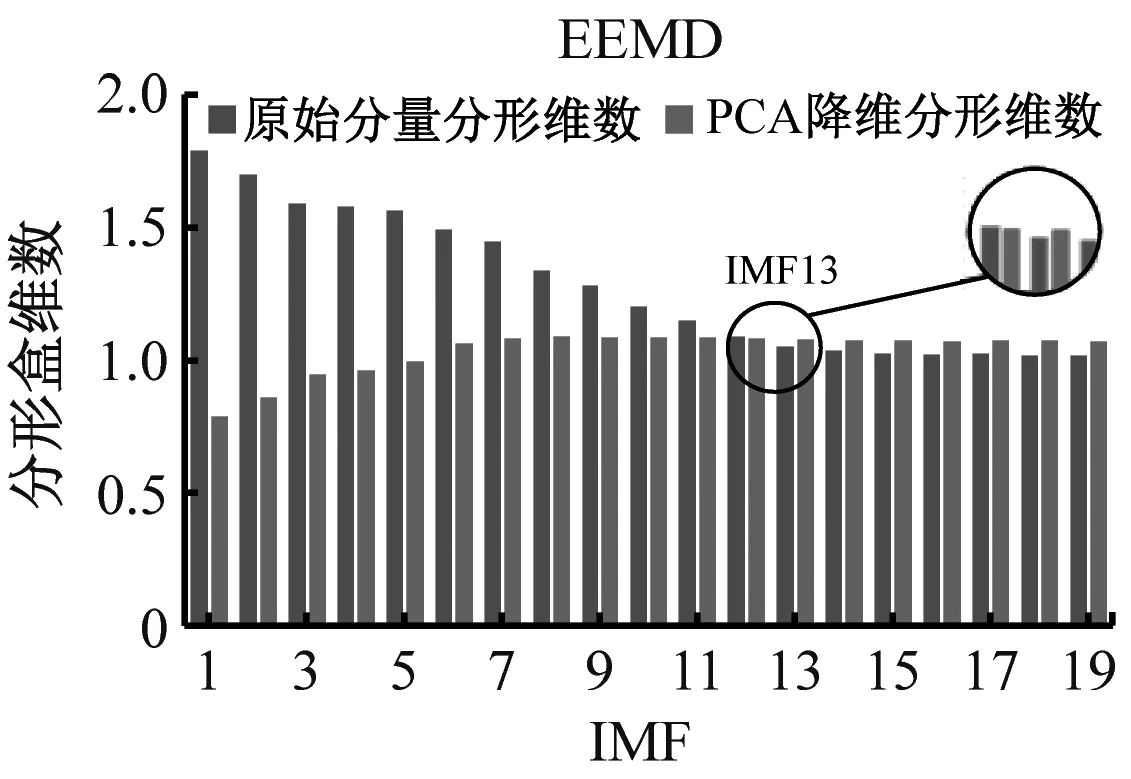
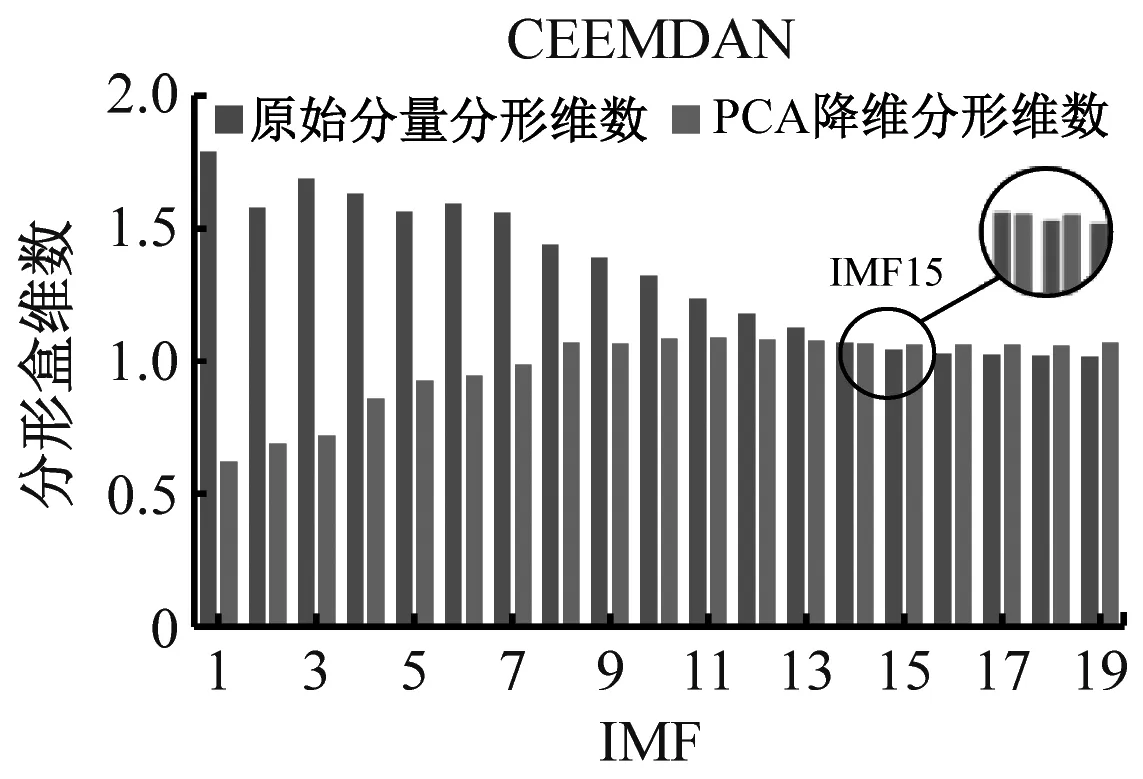
(d) 保持架磨损图10 不同方法对各故障最佳重构分量的筛选Fig.10 Screening of different methods to the optimal reconstructed components of each fault
由图10可知,降维前后分形盒维数呈现负相关现象且CEEMDAN算法明显优于EMD和EEMD算法,基于分形盒维数性质,盒维数大小与信号稳定性呈负相关。PCA降维前,IMF分量中的残余噪声会直接影响整体的稳定性,导致盒维数随IMF分量逐渐减小;降维后,主要故障信息被进一步提取、净化,增强了数据稳定性。通过交叉确定最佳重构分量,不仅可避免残余噪声的影响,还能剔除冗余分量和虚假分量。各故障最佳重构分量时域图如图11所示,其中内圈磨损2代表已重构内圈信号,其余类同。
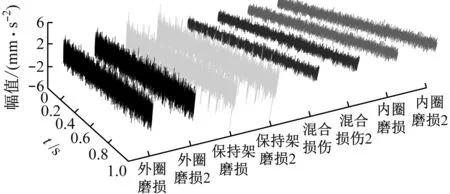
图11 最佳重构分量与原始信号分量时域图Fig.11 Time domain diagram of optimal reconstruction components and original signal components
4.3 鲁棒性验证
根据改进CEEMDAN筛选的最佳重构分量,采用CNN方法验证并与改进EMD、EEMD算法进行对比。将原始信号按8∶1∶1比例进行训练、测试及验证,同时采用重采样方法增加样本数量,提高其识别精度。在无噪声下,最佳重构分量的训练集准确率和损失情况如图12所示。
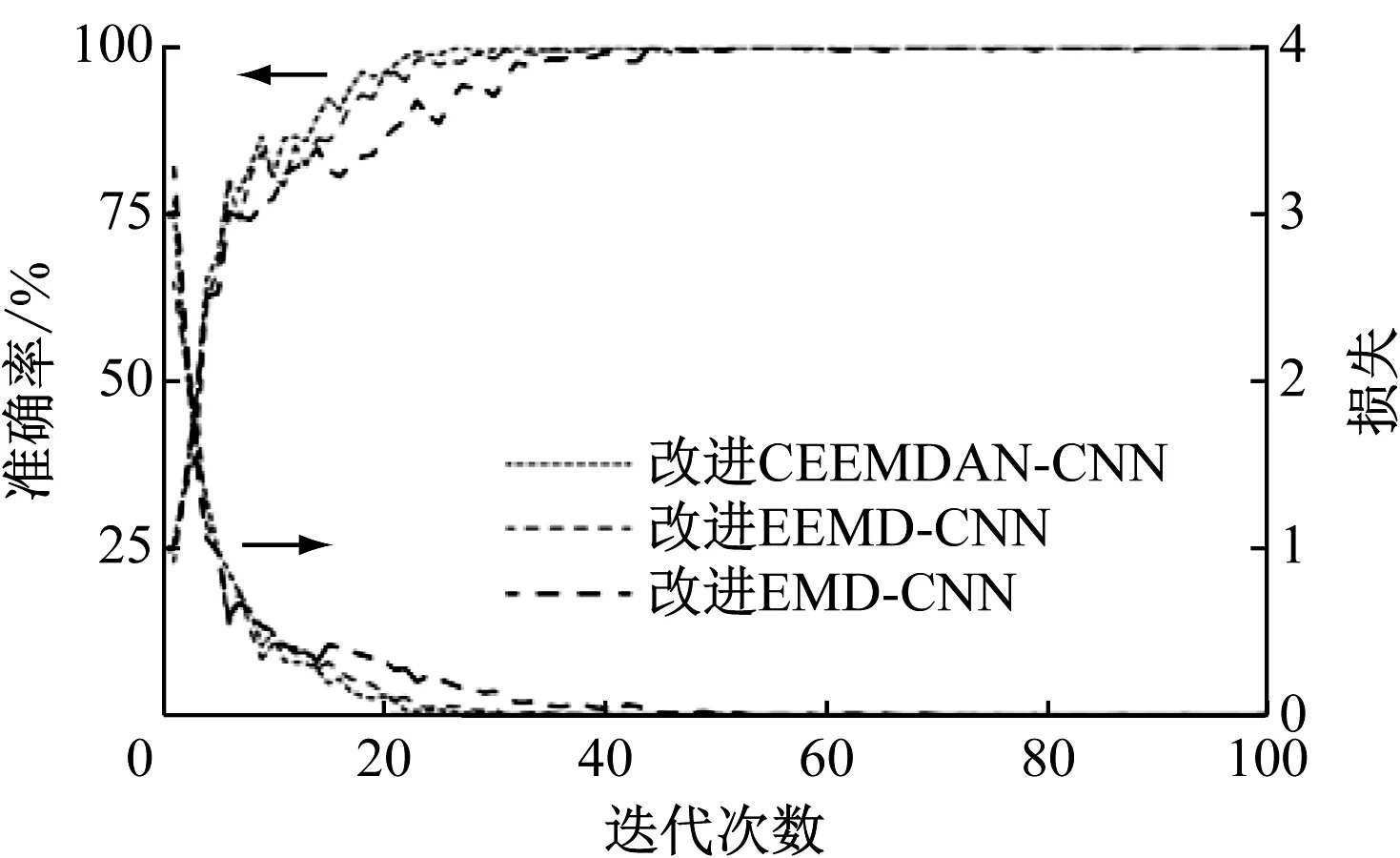
图12 最佳重构分量的训练集准确率和损失Fig.12 Accuracy rate and loss of training set for optimal reconstruction components
由图12可知,改进CEEMDAN-CNN算法的准确率及损失均优于其他算法,具有较好的鲁棒性和可行性。而实际环境中存在混杂噪声,为进一步验证该方法的实用性和泛化性,需尽可能还原实际运行环境,在信号中添加不同信噪比的噪声。
4.3.1 可视化
鉴于直观性,采用t-SNE方法对改进CEEMD-NAN-CNN算法在无噪声下的各层进行可视化,结果如图13所示。

(a) 卷积层1

(b) 卷积层2

(c) 卷积层3

(d) 卷积层4

(e) 卷积层5

(f) 全连接层

图13 改进CEEMDNAN-CNN算法各层可视化分析结果Fig.13 Visualization results of each layer for improved CEEMDAN-CNN algorithm
4.3.2 泛化性验证
为进一步还原实际运行工况,需在原始信号中添加不同信噪比的噪声,各方法不同信噪比下的识别准确率如图14所示。

图14 各方法不同信噪比下的识别准确率Fig.14 Recognition accuracy of each method under different SNR
由图14可知,与其他算法相比,改进CEEMDAN-CNN算法有显著的优越性和良好的泛化性。信噪比可较好地还原实际运行环境,而其与准确率呈正相关,间接反映了噪声对诊断精度的影响。与原始算法相比,改进算法筛选最佳重构分量具有更高的识别与分类精度;所提方法准确率最高可达99.79%,在-6 dB信噪比时识别精度仍有87.13%,较其他算法提高了0.54%~10.33%;改进后的算法可较好地剔除冗余信号与虚假分量并实现降噪,增强有效故障体征提取的准确性,进一步提高了故障诊断识别与分类精度。
5 结 论
(1) 所提改进CEEMDAN-CNN算法可较好地滤除噪声干扰并准确提取有效的故障特征,减小诊断误差。
(2) 采用PCA降维与分形盒维数结合方法筛选最佳重构分量,可有效剔除冗余分量与虚假分量,从而提高CNN故障识别与分类精度,通过对不同工况下滚动轴承进行故障分析,验证了所提方法具有较强的鲁棒性和实用性。
(3) 相比现有方法,本文改进CEEMDAN融合CNN方法在不同信噪比下均具有较高的识别精度,准确率最高可达99.79%。
