基于串联形式智能融合算法的燃气轮机建模与仿真
2022-07-30荀金柱
李 薇, 何 兴, 许 野, 荀金柱, 王 旭, 包 哲
(华北电力大学 环境科学与工程学院, 北京 102206)
近年来,燃气轮机由于对燃料适应性强、启动速度快、功率密度大等优势,已普遍应用于诸多行业,对人类社会发展有着极其重要的作用。其中,以燃气轮机为核心的冷-热-电三联供系统,由于其能源梯级利用、污染物排放低、靠近用户、能源供应安全和运行方式灵活等优点,在世界范围内得到了大规模的推广和应用。燃气轮机仿真模型的构建有助于精确地估算其发电量和余热量,发电量影响联供系统其他发电设施的功率,余热可被溴化锂和余热锅炉利用分别产生冷量和热量。因此,构建合理、可靠的燃气轮机仿真模型至关重要,其准确性将直接决定整个系统的运转情况。
目前,常用的燃气轮机建模方式包括2类:机理建模方法和人工智能建模方法。其中,机理模型基于能量、质量、动量守恒等原理,对各个部件的运行过程进行细致的刻画和描述,因此得到了广泛应用。王伟[1]通过分析燃气轮机的工艺与运行原理,采用机理和经验2种方法进行仿真建模,对燃气轮机的燃烧控制进行了深入研究。陈亚新等[2]构建了压气机机理模型,实现了定转速与变转速2种工况下压气机运行特性的动态仿真。Kim等[3]搭建了重型燃气轮机的动态仿真模型,准确识别了有助于提升模拟精度的压气机关键性能参数。Tzolakis等[4]通过机理模型与数学规划算法的结合,提高了燃气轮机的一次能源利用率和整体的热效率。上述研究在一定程度上反映了机理模型的实用性,但是由于燃气轮机的各部件之间耦合关系复杂,个别部件特性难以获取,导致其关键性能参数的识别存在困难;另外,燃气轮机的运行年限也会对性能参数产生影响,导致机理模型普遍存在构建难度大、精度低等缺陷[5]。
近年来,随着人工智能技术的快速发展,包括BP神经网络在内的人工智能算法开始不断涌现,并在很多领域得到了广泛的应用[6]。由于人工智能算法不必考虑燃气轮机内部的运转过程,只需将整个系统作为黑箱处理,运用大量数据进行训练学习,即可简单而有效地完成动态仿真建模。因此,基于人工智能算法的燃气轮机仿真建模研究受到了国内外学者的广泛关注。吴越文[7]完成了适用于实时仿真的设备模块化建模,并建立了系统仿真平台,为综合能源系统的深入研究奠定了基础。张乔斌等[8]采用径向基函数BP神经网络建立了燃气轮机动态仿真模型,利用该模型可以对燃气轮机进行有效的状态监测与维修。Anvari等[9]以冷-热-电三联供系统的主体设备燃气轮机为研究对象,分别构建了机理模型和基于BP神经网络的智能预测模型,结果显示智能预测模型的拟合效果更佳。Asgari等[10]总结了以神经网络为基础的燃气轮机系统识别、仿真和控制的相关研究,为燃气轮机智能仿真模型的构建提供了参考。
尽管人工智能算法在无需详细了解设备的内部结构和原理、自主学习与快速寻找最优解等方面体现出了一定的优势,但是其存在缺乏理论支持、过分依赖样本数量和质量以及外延性较差等缺陷,在一定程度上制约了该算法在燃气轮机仿真建模领域中的应用。考虑到机理仿真建模与人工智能仿真建模都存在一些问题,实现二者有机组合、优势互补的智能融合算法可以更好地反映系统的运转规律与特性。陈坚红[11]建立了燃气轮机基于机理和BP神经网络算法的智能融合模型。综上所述,智能融合算法很好地实现了人工智能算法与机理模型的优势互补,预测精度明显高于单一建模方法,提高了模型的准确性与可靠性,具有广阔的应用前景。
考虑到目前的智能融合模型多数使用BP神经网络和支持向量机等传统人工智能算法,普遍存在计算量大、泛化能力差、收敛速度较慢和经常出现局部最优解等问题,影响了智能融合模型的模拟精度[12]。因此,笔者在建立燃气轮机机理模型的基础上,选用可以有效处理自变量与因变量之间复杂的线性与非线性关系且能够处理连续及离散型随机变量的逐步聚类分析法(Stepwise Cluster Analysis,SCA)来代替传统的人工智能算法,构建串联形式的智能融合模型。以辽宁某钢厂的燃气轮机为建模对象来验证智能融合模型的实用性和可行性。
1 基于智能融合算法的燃气轮机仿真模型构建
1.1 总体思路
将燃气轮机分为压气机、燃烧室和透平3个模块,在分别构建3个部件机理模型的过程中,发现压气机模块的机理仿真存在一定困难,采用逐步聚类分析法和传统的BP神经网络算法分别构建压气机智能预测模型,并将其与燃烧室、透平的机理模型进行组合,构建了2套串联形式的智能融合模型;通过对智能融合模型与单一的机理模型和智能预测模型的仿真结果进行对比,凸显出智能融合模型的先进性。图1展示了本文的技术路线。

图1 技术路线图Fig.1 Technical roadmap
1.2 燃气轮机机理模型构建
燃气轮机是将热能转换为机械功的旋转式机械,其工作原理是通过压气机连续地从外界中直接吸入空气并且进行压缩,经过压缩后的高压空气进入燃烧室与喷入的燃料混合燃烧,产生的高温燃气再进入透平模块膨胀做功。其中大部分功用来驱动压气机继续压缩空气,剩下的功用来驱动发电机发电。如上所述,燃气轮机机理建模的核心是将3个模块的划分与关联抽象出来,结合部件的关键参数、特性曲线与实际运行情况对每个模块进行理论建模。
1.2.1 压气机模块机理模型
压气机模块关键参数主要包括出口压强p2,出口温度T2和消耗功率Nc。
p2=π·p1
(1)
(2)
(3)
式中:p1为压气机的进口压强,即为外界环境压强,取101.325 kPa;π为压气机的压比;T1为压气机的进口温度,即为外界环境温度,取288.15 K;ka为运行过程中比定压热容与比定容热容之比(即比热容比),取1.4;ηs为压气机效率;qm,1,in为空气质量流量, kg/s;cp,a为空气比定压热容,kJ/(kg·K)。
1.2.2 燃烧室模块机理模型
燃烧室关键参数主要包括燃料质量流量qm,r和出口烟气温度T3。
(4)
(5)
式中:Ngt为燃气轮机实际输出功率,kW;ηr为燃烧室燃烧效率;qr为燃料低位热值,J/kg;qm,2,in为燃烧室进口燃料质量流量,kg/s;hr为燃料的物理焓,J/kg;cp,g为燃料的比定压热容,J/(kg·K);qm,2,out为燃烧室出口烟气质量流量,kg/s。
1.2.3 透平模块机理模型
透平部件关键参数主要包括透平出口烟气温度T4、输出功率NT和燃气轮机实际输出功率Ngt。
(6)
(7)
Ngt=ηgr(NT-Nc)
(8)
式中:T3为透平的进口烟气温度,即为燃烧室出口烟气温度,K;πT为透平膨胀比;ηT为透平效率;kg为燃气平均比热容比,取1.33;ηgr为燃气轮机发电效率。
1.3 基于逐步聚类分析法的燃气轮机智能预测模型构建
逐步聚类分析法基于多元方差分析理论,根据特定的标准将原始的因变量集划分为许多不相关的子集,然后再根据规则进行合并,经过反复多次的切割和合并操作,在所有进一步的切割或合并假设都被拒绝后,最终生成反映变量之间复杂关系的聚类树,可用于未来预测。逐步聚类分析法可以有效处理连续和离散变量以及变量之间的非线性关系,相较于一般数学函数,生成的聚类树可以灵活地反映多个独立变量与因变量之间复杂的相互作用[13-14]。因此,本研究采用聚类树来反映燃气轮机输入变量与输出变量之间的复杂关系。其中,切割或合并的标准是基于Wilks值(W)的Λ统计量,具体计算公式如下:
(9)
(10)
(11)
(12)
(13)

由F近似理论可知,2个样本的Wilks值与F-统计量具有如下关系:
(14)
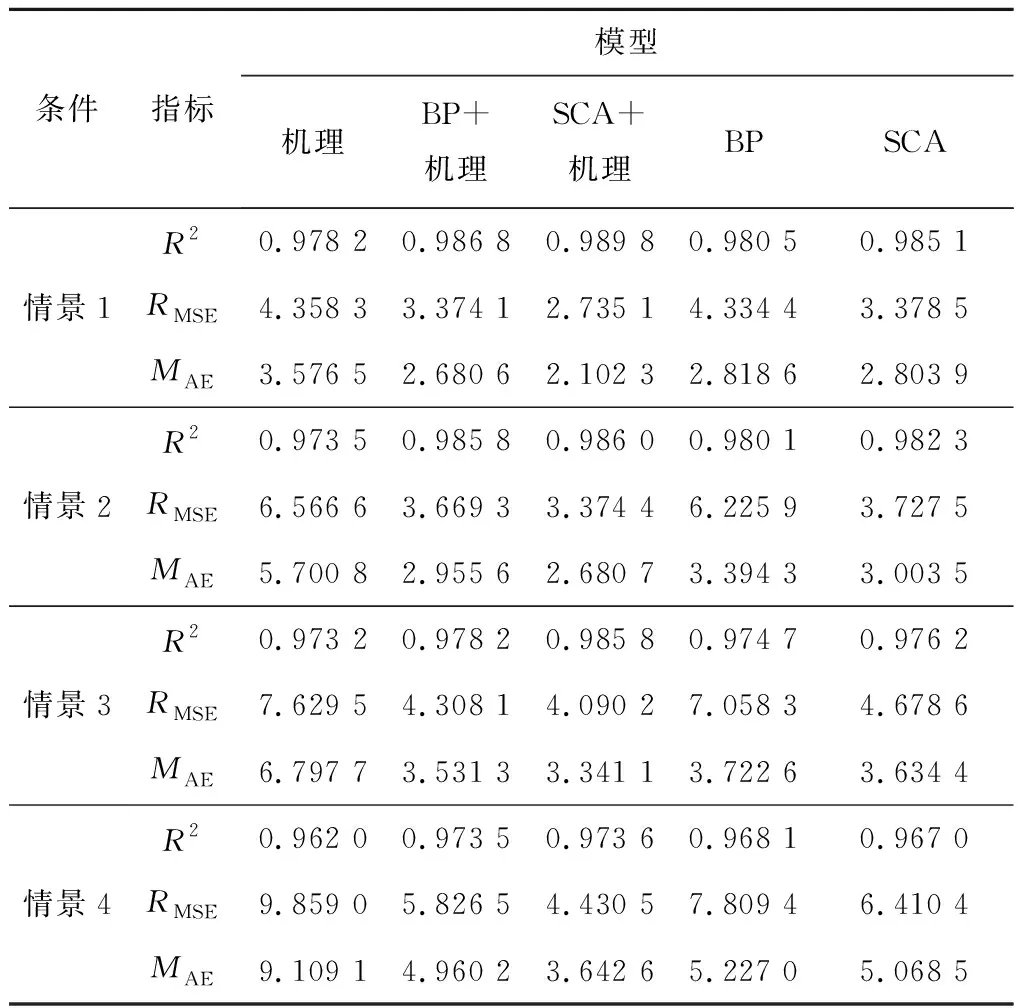
由Wilks的似然比标准可知,Λ值越小,e与f之间的差异越大。因此,可以采用F检验来比较这两组因变量的差异。零假设为H0:μe=μf;替代假设为H1:μe≠μf,其中μe和μf分别为e和f的总体均值。显著性水平定义为α,当F≥Fα时,H0为假,表明这两组之间的差异显著,允许切割;而合并标准是F 考虑到传统的机理建模方法包含大量假设与统计信息,存在过分简化以及无法有效反映燃气轮机多变量、强耦合等特点;人工智能算法无需详细了解设备的内部结构和原理,但其建模过程严重依赖数据质量,缺乏物理基础。智能融合模型的主体思想是将人工智能预测技术充分融合到机理建模过程中,确保已有的对象信息(如历史数据、生产经验等)得到充分利用,形成具有一定智能特色的对象系统描述结构。目前,常见的智能融合模型形式有串联和并联2类[15]。其中,串联结构主要用于过程机理模型中某些方程缺失或者方程中某些参数无法准确识别,且该过程具有大量的输入、输出数据可供使用的情况。在此条件下,使用智能预测模型去描述未知过程,将预测值代入机理模型中,利用机理模型作为整个智能融合模型的基础模型来完成预测。 如前所述,压气机运行过程复杂和参数不易获得的特点导致机理模型的构建存在很大困难[16]。因此,为了保证仿真结果的准确性,本研究选择压气机的进口温度、进口压力和压比作为输入变量,出口温度和压气机功率作为输出变量,构建了基于逐步聚类分析法的压气机仿真模型;然后,将输出参数作为后续燃烧室、透平的机理模型的输入变量,形成串联形式的智能融合模型;最后,以发电量为最终输出参数,对比实际运行数据,选定平均绝对差值(MAE)、均方根误差(RMSE)和决定系数R2作为模型的评价指标,定量评估该智能融合模型的有效性和实用性。 (15) (16) (17) 辽宁某钢厂占地面积约为220 hm2,具有自备发电设备,用于完成自供任务。厂区内设有3台以动力煤为主要燃料、高炉煤气为辅助燃料的火力发电机组和1台燃气-蒸汽联合循环发电机组,后者以高炉煤气与焦炉煤气混合气体为燃料。以工业重型M701S-DAX燃气轮机为研究对象,其主要参数如下:转速为3 000 r/min;发电机额定容量为110 MW。煤气压缩机型式为轴流式,其体积流量为344 380 m3/h。压气机压比为15∶1,压气机效率、燃烧室燃烧效率、透平效率和燃气轮机发电效率分别为0.88、0.89、0.90和0.75。尽管燃气轮机各个部件的效率在不同工况条件下存在一定的差异,但是对燃气轮机运行情况的实际调查和统计结果显示,上述效率值均在较小区间范围内波动。因此,本研究取其平均值作为燃气轮机的关键性能参数。 为了更好地考察仿真模型的可靠性,反映训练样本量对仿真模型精度的影响,随机选取5 000组、4 000组、3 000组和2 000组数据用于模型构建,另选取1 000组数据进行验证,分别命名为情景1~情景4,以MAE、RMSE和R2作为模型的评价指标。图2为4种情景条件下各个模型的仿真结果对比图。除了前述提到的机理模型、基于逐步聚类分析法的压气机仿真模型以及二者的智能融合模型(SCA+机理模型)以外,本研究还分别构建了基于BP神经网络的燃气轮机整机仿真模型(以下简称BP模型)和基于逐步聚类分析法的燃气轮机整机仿真模型(以下简称SCA模型)以及BP神经网络和机理模型的智能融合模型(BP+机理模型),以此来比较逐步聚类分析法和传统智能预测算法的差异性,更好地反映了智能融合模型的优势。由图2和图3可知,4种情景条件下各模型预测结果与实测值的总体变化趋势基本一致,但各模型的模拟精度存在一定差异。 (a) 情景一 (b) 情景二 (c) 情景三 (d) 情景四图2 不同情景条件下各模型的预测结果对比Fig.2 Predicted results comparison of all models under various scenarios (a) 情景1 (b) 情景2 (c) 情景3 (d) 情景4图3 不同情景条件下各模型的模拟精度对比Fig.3 Prediction-accuracy comparison of all models under various scenarios 表1 燃气轮机仿真模型模拟效果对比Tab.1 Comparison of simulation effects of all models for the gas turbine 图3给出了4种情景条件下各模型的模拟精度对比。由图3可知,4种情景条件下智能融合模型的2类误差指标最好。表1则给出了更为直观、详细的对比结果。首先,如表1所示,5种仿真模型的R2均超过90%,具备一定的可信度。其中,3种单一仿真模型中,机理模型的模拟精度最低,4种情景条件下均方根误差为4.358 3~9.859 0,平均绝对差值为3.576 5~9.109 1,R2为0.962 0~0.978 2。2种智能预测模型的模拟效果相对更好,其中基于逐步聚类分析法的智能预测模型的均方根误差为3.378 5~6.410 4,平均绝对差值为2.803 9~5.068 5,R2为0.967 0~0.985 1。基于BP神经网络的智能预测模型的均方根误差为4.334 4~7.809 4,平均绝对差值为2.818 6~5.227 0,R2为0.968 1~0.980 5。其主要原因在于,燃气轮机运行时容易受外界条件干扰,且部件特性曲线和设计参数难以获取。尽管通过一些简化和假设可以得到经验关系式,却不可避免地存在误差。因此,机理模型的拟合表现最差。相较于机理模型,智能预测模型在数据量充足、燃气轮机运行状态比较稳定的前提下,可以忽略内在机理,发挥其强非线性映射优势,准确地捕捉到系统关键输入变量与输出变量之间的关系。至于2种单一智能预测模型,其对比结果显示基于逐步聚类分析法的智能预测模型的总体表现更好,其精确度较高、拟合优度较好。这主要是因为BP神经网络模型存在权值初始化机制不清和容易陷入局部最优等缺陷;相反,逐步聚类分析法根据预先建立的基于切割和合并标准建立的聚类树,可以准确识别变量之间的复杂关系,因此具有极佳的拟合表现。 其次,2种串联形式的智能融合模型的均方根误差与平均绝对差值均小于上述3种单一仿真模型。其主要原因在于,与单一仿真模型相比,智能融合模型实现了机理和智能预测模型的优势互补。一方面,基于智能预测算法的压气机仿真模型根据掌握的输入和输出变量值,直接建立二者之间的响应关系,有效克服了机理建模过程中遇到的特性曲线难以获得和参数取值困难等问题;另一方面,智能融合模型中的燃烧室与透平模块采用机理建模方法,可以充分运用质量、能量、动量守恒等基本定律以及掌握的历史数据、生产经验等对象信息,弥补了智能预测算法缺乏理论基础和外延性较差等的缺陷。 最后,2种智能融合模型的对比结果显示,基于逐步聚类分析法的智能融合模型模拟精度更高。其主要原因在于,如前所述,利用BP神经网络模型对压气机模块建模,尽管优于传统的机理建模方式,但是仍然会出现由于权值不定而使结果陷入局部极小值的情况,最终影响了智能融合模型的模拟精度。由此可见,基于逐步聚类分析法的智能融合模型整体表现更佳,推荐用于考察燃气轮机变工况条件下的整体表现。 以辽宁某钢厂燃气轮机为研究对象,通过建立包括单一机理、智能预测模型和智能融合模型在内的5种燃气轮机仿真模型,模拟得到其变工况条件下的发电量;在此基础上,利用平均绝对差值、均方根误差和决定系数来评估各类仿真模型的性能。对比结果显示,智能融合模型的表现明显优于单一仿真模型,其中基于逐步聚类分析法的智能融合模型的模拟精度最高。 本文创新性地构建了基于逐步聚类分析法的燃气轮机智能融合模型。但是,仍然存在一些问题有待解决:(1) 在数据样本集的准备过程中,只是通过简单计算进行数据筛选和剔除少量异常值,后续可以考虑使用K-means聚类法与马氏距离法完成数据预处理,为提高仿真模型的精度奠定基础;(2) 仅仅采用BP神经网络和逐步聚类分析法完成智能预测,并未使用卷积神经网络、循环神经网络等深度学习算法建立模型,无法很好地考察和反映智能融合模型的优越性。1.4 智能融合模型构建
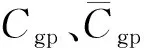
2 案例分析
2.1 案例概述
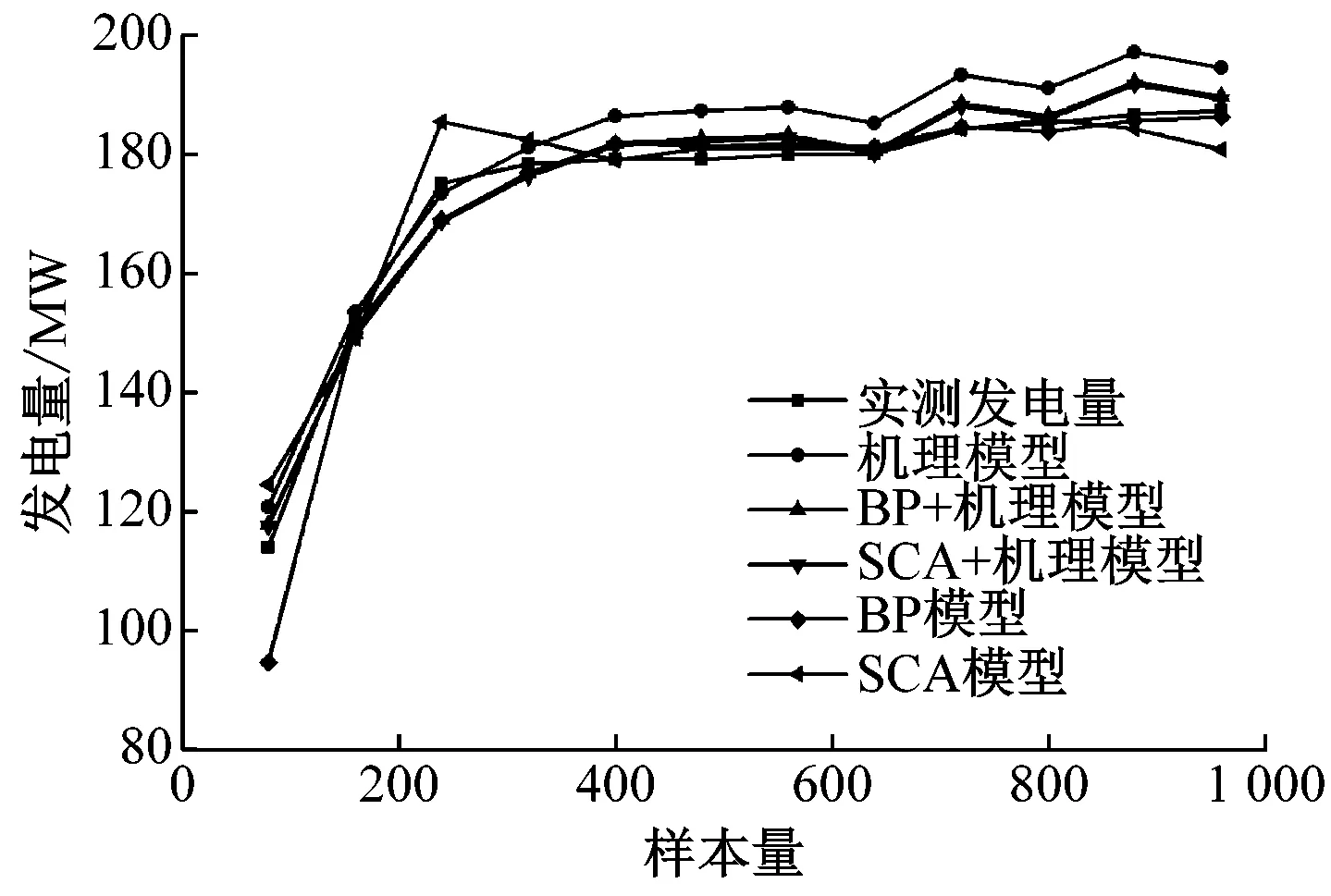
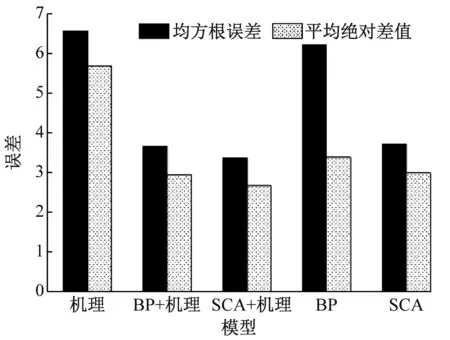
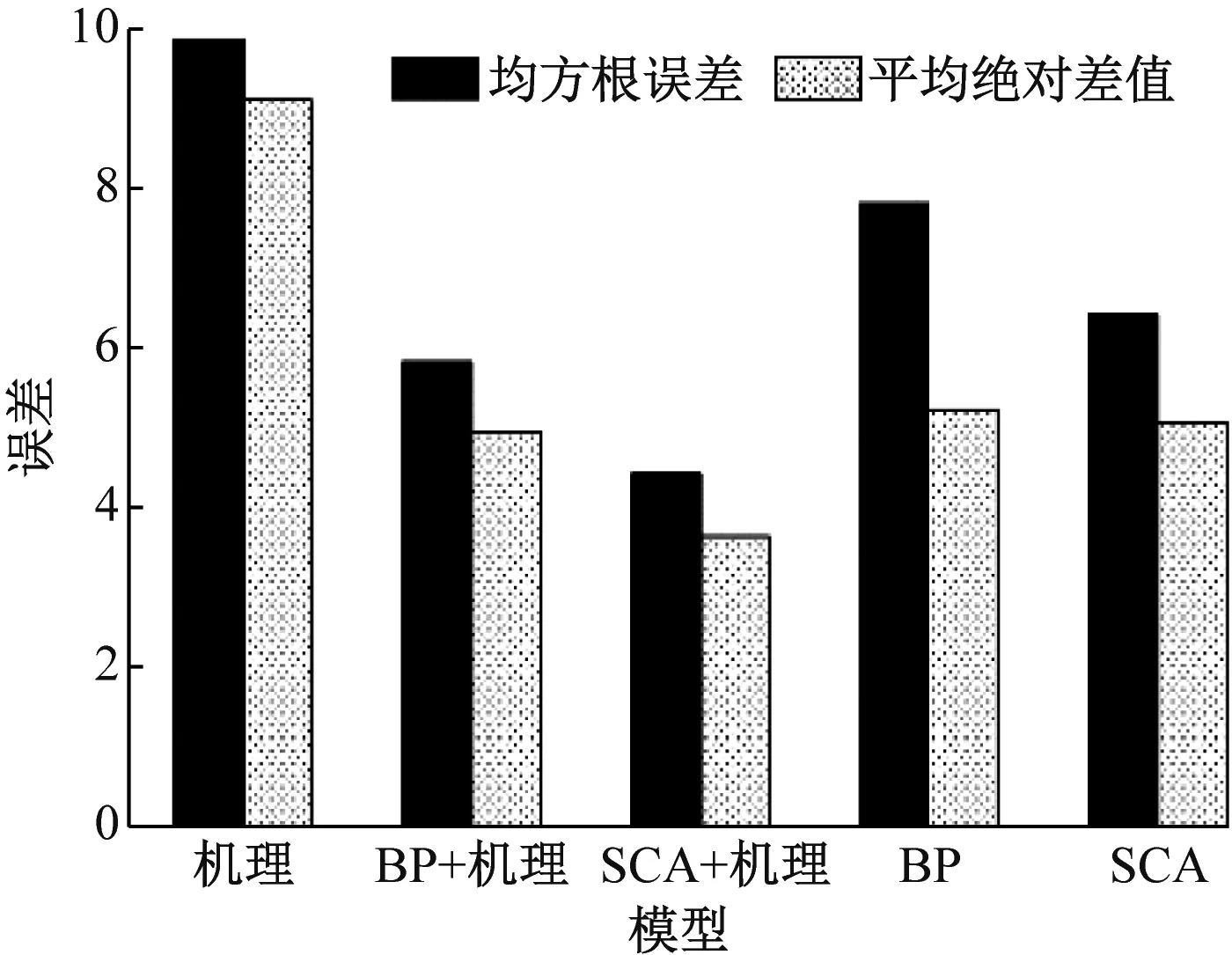
2.2 结果分析





3 结 论
