强干扰环境下声源可视化重建方法的研究进展
2022-07-29蒋伟康
李 豆,蒋伟康
(上海交通大学机械系统与振动国家重点实验室,上海 200240)
0 引言
准确识别噪声源,确定其位置、分布和贡献量,是机电产品低噪声和声质量设计的关键技术。用于空调、冰箱、洗衣机、油烟机、破壁机、吸尘器等家电产品的低噪声设计,可以改善人们的工作和生活环境;用于民用车辆、船舶、飞机、工程机械等的振动噪声控制,可以提高乘坐及操作舒适性。随着研究工作的不断深入,噪声源辨识方法已从最早的依靠主观经验判断、表面声场测量等方法逐渐演变成更先进的以波束形成(Beamforming,BF)技术[1-2]、近场声全息(Nearfield Acoustic Holography,NAH)技术[3-5]等为代表的新型方法。其中,BF 和NAH 方法分别适用于远场高频和近场低频声源的重建。
传统的NAH 和BF 基于自由场假设,要求目标声源辐射声与干扰噪声的信噪比大于 10 dB。但很多机电产品的噪声测试只能在生产、试验和使用现场进行,不满足自由场条件。目标声源的辐射声场可能会受到邻近相干噪声源的辐射噪声、来自壁面及周围其他散射体的散射声场以及背景噪声等的干扰。强干扰环境即目标声源辐射声与干扰噪声的信噪比小于10 dB 的情况,其中,干扰噪声包括了辐射噪声、散射声以及背景噪声等。如果在封闭空间内,还需要考虑混响的影响。对于低频噪声源,采用近场测量方式进行重建时,采集到的直达声的能量通常大于混响声能量,混响影响不大;但对于高频噪声源远场测量重建,混响不可忽略。在这些强干扰环境下,传统的NAH 和BF 方法无法准确重建噪声源,不能有效指导噪声和振动控制,增大了机电产品样机降噪的成本和周期。
本文的声源重建方法包括了声源表面各声学量的重建以及声源定位等,主要分为基于声学传播方程的声源重建和基于信号处理的声源重建两大类进行介绍。其中,基于声学传播方程的声源重建方法包括基于声场分离方法的声源重建、基于逆块传递函数法的声源重建、混响环境下的声源定位和循环平稳声场重建。基于信号处理的噪声分离方法包括基于子空间的方法和基于信号噪声不同特性的方法。
1 基于声学传播方程的声源重建方法
1.1 基于声场分离方法的声源重建
传统近场声全息方法适用于自由场环境,即传声器采集的声压只来自目标声源的辐射声。当传声器阵列远离目标声源的一侧存在干扰源且信噪比低于10 dB 时,传统近场声全息方法无法实现声源的准确重建。声场分离技术(Sound Field Separation Technique,SFST)就是要分离出目标声源以外的干扰源,用自由场下的近场声全息方法进行声源重建。SFST 的声场分离模型如图1 所示。传声器阵列设置在目标声源与干扰源之间。首先,采用双声压测量面、双速度测量面或单层声压速度测量面获得目标声源近场声学量。然后,将采集到的声场信息分解为后传声波和前传声波,其中,后传声为干扰源的辐射声,前传声波包含目标源辐射声,以及干扰源在目标声源表面反射产生的散射声,再根据目标声源表面的阻抗条件分离出该散射声,获得目标声源在自由场下的辐射声。

图1 声场分离模型 Fig.1 The model of sound field separation technique
SFST 根据所采用的传播算法不同可以分为基于空间傅里叶(Fourier)变换的SFST[6-17]、基于边界元的SFST[18-24]、基于等效源的SFST[25-33]、基于统计最优的SFST[34-38]和基于patch 方法的SFST[39-40]等,这些方法的主要特点有:基于空间Fourier 变换的SFST 适用于规则形状声源重建;基于边界元的SFST 和基于等效源的SFST 适用于不规则形状声源重建;基于统计最优的SFST 和基于patch 方法的SFST 适用于局部声源重建。上述SFST 中,干扰源位于阵列远离目标声源的一侧且位置未知。基于单层全息面的声场分离方法与此不同,干扰源位置已知,位于目标声源同侧或异侧,根据声学传播方程可以重建目标声源的表面声学量。下面介绍这五种SFST 的原理以及目前的研究现状。
1.1.1 基于空间Fourier 变换法的声场分离方法
1990 年,Tamura[6]提出了基于空间Fourier 变换的斜入射声压反射系数测量方法,根据平面波传播特性分离入射波和反射波,得到任意入射角下的反射系数。随后,Tamura 等[7]对该方法进行了实验验证。2005 年,合肥工业大学Yu 等[8]提出了基于平面和柱面空间Fourier 变换的SFST,通过双层声压测量,或者单层声压速度测量,分离前传和后传的声波,实现声源面声压和粒子振速等声学参量的重建。2014 年,作者同团队的Hu 等[10]使用双层声压测量面分离前传和后传声波,然后利用声源表面的刚性边界条件进一步从前传声波中分离出散射波,得到目标声源在自由场中的辐射声场。该团队还提出了基于声强测量的宽带声全息方法[11]。Zea 等[12]使用单层声压测量,在声源面和反射面的导纳已知的条件下,分离了有平行反射面的平面声源辐射声场。
基于空间Fourier 变换的SFST 计算速度快,但只适用于平面、柱面和球面等规则形状,要求全息面和声源面共形;其次,由于该算法中全息面数据是在有限孔径上测量得到的,窗效应和卷绕是影响重建误差的重要因素。
1.1.2 基于边界元法的声场分离方法
1999 年,Kim 等[18]提出了基于边界元的SFST,基于边界元的测量技术和局部响应假设,估计空腔边界的阻抗,然后重建封闭空腔内的辐射声场。Langrenne 等[19]使用双声压测量面采集声压,再采用均值和差分算法,获得测量面的声压和振速,分离出前传声波,再根据刚性边界条件分离散射声,重建了噪声干扰环境下机械设备的辐射声压。Langrenne 等[21]还提出了在同一全息面上测量声压和速度,识别半空间中的声源。为了解决基于边界元的SFST 不能用来进行局部重建的问题,Valdivia等[20]提出了基于间接边界元法的SFST。为了提高噪声环境下声源重建的效率,Wu[22]提出了基于修正的亥姆霍兹(Helmholtz)最小二乘和边界元的混合声全息方法。基于修正的Helmholtz 最小二乘法和双声压测量,分离后传声波,计算出全息面上更多测量点处的声压值,再根据边界元法重建声源表面的声学量。Wu 等[23]提出了基于双层声压测量的边界元声场分离方法,两个测量面以及测量点的布置自由,降低了测试成本以及仪器对声场的干扰。毕传兴团队提出了基于边界元的声场分离方法,全息面测点位置不受限制,采用三维扫描技术获得测点坐标[24]。
基于边界元的STFT 适用于任意形状的全息面和声源面。另外,近年来边界元方法的发展解决了奇异性[41]和共振频率处的求解非唯一性[42]等问题,大大拓展了其在近场声全息上的应用范围。基于边界元法的近场声全息,虽然利用积分方程建立了声源和辐射声场的直接联系,但全息面及测点位置对声场重构算子特性及重建结果影响的机理还不够清晰,只能通过网格离散经验或者仿真,并应用正则化技术进行声场重建。
1.1.3 基于等效源法的声场分离方法
毕传兴团队2008 年提出基于等效源的SFST,并采用双层声压测量来分离后传声波[25]。之后,他们不断发展该方法,提出了利用刚性边界条件来分离散射声[26]。Fernandez 等[27]研究了基于等效源的SFST 中声压速度测量和双速度面测量之间的差异,结果表示声压速度测量更为稳健。毕传兴团队使用基于等效源法的声场分离方法重建振动结构体表面振速,根据刚性边界条件分离散射声,比较了双声压测量和双速度测量之间的差异,指出双声压测量在速度重建中更占优势[28]。基于等效源的SFST应用于空腔内[30]以及半空间中[31]的可行性已被证实,其中,空腔内声源重建时,散射声根据刚性边界条件进行分离。最近,毕传兴团队又将基于等效源SFST 拓展到稀疏框架下,使用压缩感知方法进行声场分离和声源重建[33]。
基于等效源法的STFT 不仅适用于任意外形声源,而且全息面数据和声源面声学量之间的传递矩阵构造简单,提高了计算效率。但是等效源一般不具备正交性,布置不合理可能会导致传递矩阵严重病态,求解误差大。如何在未知声源特性的情况下合理布置等效源值得继续研究。
1.1.4 基于统计最优法的声场分离方法
基于统计最优的SFST 适用于局部声源声场分离和重建。Hald 等[34]应用基于统计最优的SFST,采用双层声压测量分离前传和后传声场,然后根据声源表面的吸声系数或导纳来消除散射声强,重建了座舱壁板的辐射声强。Jacobsen 团队研究了基于统计最优的SFST 在双层声压测量和单层声压速度测量下的差异,结果表明在强干扰环境下,两种方法之间没有显著差异[35];并针对阵列两侧的干扰源和声源不对称的场合,进一步改进了基于统计最优的SFST[36];证明了基于双层声压测量的统计最优SFST 比基于单层声压速度测量的SFST 更具鲁棒性[37]。
统计最优STFT 可以实现声源局部重建,即不要求全息面尺寸必须大于整个声源面。但该方法只适合平面和柱面等规则外形的声源,同时测量点和重建点对重建误差的影响也不够清晰,工程应用受到一定限制。
1.1.5 基于patch 法的声场分离方法
基于patch 方法的近场声全息和SFST 相结合可以实现局部声源重建。毕传兴团队提出了一种双面patch 近场声全息技术,首先应用基于Fourier 变换的SFST 分离出前传声波,再基于波数域外推算法进行声源局部重建[39]。随后,该团队又提出了基于等效源的双面patch SFST,并在汽车舱室内实现了扬声器辐射声场的重建[40]。
Patch STFT通过人为增大测量孔径来实现声源局部重建,也继承了所采用的近场声全息方法固有的局限性。
1.1.6 基于单层全息面的声场分离方法
首先介绍干扰源与干扰源位于阵列同侧的情况。2004 年,毕传兴团队[43]建立了基于分布源边界点法[44]的多源声场重建理论,提出了单面测量组合法、多面测量组合法和多面测量消元法三种方法,用于多个相干声源同时存在时的声源重建,并进行了数值仿真验证。随后,该团队对单面测量组合法和多面测量组合法进行了实验验证[45]。针对Helmholtz 方程最小二乘(Helmholtz Equation Least Squares,HELS)法无法准确重建多源相干声场的问题,蒋伟康团队提出了一种改进的HELS 方法,并进行了仿真验证[46-47]。
下面介绍干扰源与目标声源位于阵列异侧的情况。2009 年,上海交通大学Jia 等[48]提出了基于波叠加法的单全息面声场分离技术,在已知干扰源位置的前提下,用镜像源法和波叠加法获得重建面声压,再进行声场分离。该团队又提出了基于波叠加和统计最优近场声全息的单全息面声场分离技术[49],在已知目标声源和干扰源位置前提下,基于波叠加法和全息面声压得到重建面声压,再根据全息面和重建面声压以及统计最优近场声全息方法实现声场分离。浙江工业大学的卢奂采团队提出了基于单层传声器阵列的声场分离技术[50],在已知全息面两侧声源位置情况下,用球谐函数展开,建立全息面声压与目标声源和干扰噪声源之间的传递关系,再根据最小二乘法确定球谐函数展开项数,实现了声场分离。重庆大学的毛锦等[51]在已知目标声源和干扰源位置时,使用基于单层全息面的等效源法完成了声场分离,为了使目标声源和干扰源到全息面的传递函数不同,将等效源布置在了球面上。海军工程大学的田湘林等[52]采用了重采样的方法,将单层全息面声压测量值分为两部分,然后基于等效源方法实现了声场分离。为了保证重建精度,重建采样后得到的测点之间的距离需满足一定要求。
1.2 基于逆块传递函数法的声源重建
逆块传递函数法(inverse Patch Transfer Function Method,iPTF)由法国里昂应用科学学院(INSA)的Aucejo 等[53-54]提出,可以实现强干扰环境下的局部声源重建。该方法的基本思想是将有干扰源时的散射问题转换为无干扰源的内问题,逆块传递函数法模型如图2 所示,其中,pm和vm分别表示全息面上的声压和法向振速。内问题对应的虚拟空腔由全息面和声源面组成,全息面上需要测量声压和速度。全息面声压和声源面振速之间的阻抗矩阵基于诺伊曼(Neumann)边界条件下的格林函数获得。对于规则形状的虚拟空腔,格林函数存在解析解,如简正波格林函数。对于不规则的虚拟空腔,格林函数需要由模态叠加法构造。Aucejo 等[53]用激振器激励L 形钢板的试验,验证了所提方法可以用于不规则形状声源的局部重建。声源表面法向振速基于 截断奇异值分解(Truncated Singular Value Decomposition,TSVD)正则化方法进行求解。随后,Aucejo等[54]以障板上相位相反的两个扬声器为对象,进行了实验验证。
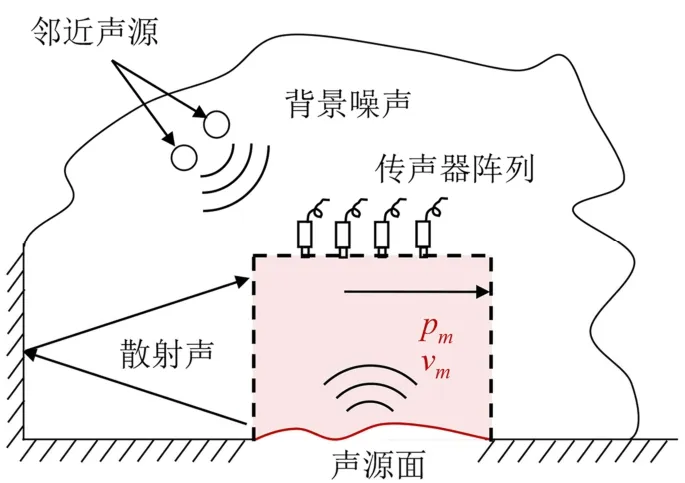
图2 逆块传递函数法模型 Fig.2 The model of inverse patch transfer function method
iPTF 方法能够在强干扰环境下实现声源表面局部振速重建,有很好的工程应用前景,之后发展了多种iPTF 方法。上海交通大学的蒋伟康团队提出了基于倏逝波格林函数的iPTF 方法[55],满足Neumann 边界条件的格林函数由倏逝波叠加得到,适用于矩形空腔,提高了计算效率和计算精度。为了改善iPTF 方法在声学测量方面的便捷性,该团队提出了基于刚性声学阵列的iPTF 方法[56],在刚性壁面上安装传声器阵列,构成刚性阵列,使得声压采集面满足Neumann 刚性边界条件,摆脱了iPTF方法中需要同时采集声压和速度的困难,只测量声压即可实现声源重建。Totaro 等[57]分别以激振器激励的平板和内燃机油底壳实验,验证了iPTF 方法,并且针对L 曲线方法有时无法得到最优解的问题,提出了一种结合L曲线和声功率守恒的正则化参数选择方法。Vigoureux 等[58]基于iPTF 方法进一步重建了嵌于障板上的钢板表面上的声压和声强,该结果同样为总声场信息。使用该方法重建不规则的声源表面的局部振速时,需用有限元法分析模态,并利用模态叠加来得到Neumann 边界条件下的格林函数,随着模态阶数的增加,计算量急剧增大。因此,Li 等[59]提出了基于自由场格林函数的iPTF 方法,避免了Neumann 边界条件下格林函数的复杂构造过程,只需要进行空腔表面二维建模,然后直接使用边界元法计算阻抗矩阵,因此,该方法不仅具有高效的阻抗矩阵构造过程,而且具有声源精确重建的潜力。另外,对于不规则形状的声源,现场测量声源表面局部几何信息费时费力,限制了iPTF方法在现场应用的前景。Li 等[60]进一步提出了基于机器视觉和iPTF 法的声源重建方法,由机器视觉三维建模方法BundleFusion 算法和RGB-D 相机建立目标声源表面的几何形状模型,并确定传声器阵列的位置,从而构建虚拟空腔模型,最终实现声源表面法向振速重建。
1.3 混响环境下的声源定位
在人们生活的房间,以及飞机、车辆等舱室中,声学环境比较复杂,声源主要包括:直达声、早期反射声和后期混响声[61]。腔体内的声场分析方法包括波动声学法和统计声学法[62-64],而且蒋伟康团队从理论上证明了在刚性边界条件下简正波理论与镜像源方法之间是等效的[65]。
Castellini 等[66]提出了一种平均波束形成方法,用于飞机舱室内的声源定位。传声器阵列在不同位置移动,将得到的波束形成结果进行平均,根据振幅和标准差来抑制反射效应。Pavlidi 等[67]通过对到达方向估计的直方图应用匹配追踪算法,联合估计声源的数量及其到达方向。Lobréau 等[68]采用双层半球形阵列进行声学测量,然后基于时间反转方法进行声源定位。Antonello 等[69]基于平面波分解和稀疏正则化来实现混响环境下的声源定位。西北工业大学的王海涛等[70]提出了基于时间反转聚焦的室内声源定位方法。
1979 年,Allen 等[71]提出了镜像源法(Image Source Method,ISM)用于模拟混响室内的脉冲响应函数。ISM 方法假定房间是矩形的,声波在房间边界上产生镜面反射。考虑在三个方向上分布的所有镜像源,将声源与接收点之间的脉冲响应函数,表达为声源和所有镜像源到接收点的贡献之和,广泛应用于混响环境下的声源反演。Villot 等[72]]提出了基于傅里叶级数的NAH 方法用于室内声场重建。室内空间为规则六面体,四周为刚性面,其余两个面为声源面和吸声面,此时空间声场相当于无数个存在对称关系的声源面产生的声场。Wang 等[73]提出了一种迭代波束形成方法进行浅水声源定位,在二维空间中使用ISM 建立声源和声压采集点之间的传播关系,然后通过迭代波束形成方法估计声源位置、源强,以及反射面的功率损耗,交替估计声源贡献并基于这些估计采用波束形成进行声源反演。ISM 中的声源和接收点都是无指向性的,为了考虑扬声器和传声器的指向性,Samarasinghe 等[74]提出了基于球谐函数的广义镜像源法,用于模拟室内声场。哈尔滨工业大学的蒋相斌等[75]基于ISM和广义互相关方法实现强干扰环境下的声源定位。基于ISM 分析声源到传声器的传播路径,然后使用广义互相关方法实现声源定位。
1.4 循环平稳声场重建
循环平稳声场是工程应用中广泛存在的一种声场环境,虽然并不存在干扰源的影响,但是此时声学信号存在严重的调制现象,传统的NAH 方法无法实现声源准确重建。2004 年,万泉等[76]提出了循环平稳近场声全息方法(Cyclostationary Near Field Acoustic Holography,CYNAH),克服了传统近场声全息方法在分析循环平稳声场方面的局限性,该方法可以广泛应用于工程中的旋转机械或者其他具有循环平稳声场特性的设备。CYNAH 的基本思想是以谱密度相关函数作为重建量,根据声学传播方程建立全息面和重建面上谱密度之间的传递关系,最终实现循环平稳声场重建。谱密度相关函数可以提取循环平稳信号的二阶时变统计量的周期性特征,因此能够用于循环平稳声场重建。根据声场空间变换算法不同,CYNAH 可以归纳为以下几类:基于空间Fourier 变换的CYNAH[76-80]、基于等效源法的CYNAH[81-82]、基于边界元的CYNAH[83]、基于 Helmholtz 方程最小二乘法的 CYNAH[84]。其中,基于空间Fourier 变换的 CYNAH 适用于平面声源,基于等效源法的CYNAH、基于边界元的CYNAH 和基于 Helmholtz 方程最小二乘法的CYNAH 适用于任意外形声源。文献[76-78]给出了基于空间Fourier 变换的CYNAH 的详细推导过程,并且以具有循环平稳特性的交流电机为对象在消声室进行了实验验证。还给出了基于空间Fourier变换的循环平稳声场重建参数的确定准则[85]。2008年,张海滨[86]在其博士论文中详细介绍了适用于任意外形声源CYNAH 的变换理论和方法,研究了影响声源重建误差的各种因素,并且进行了相应的实验研究。在循环平稳理论的基础上,万泉等[87]还提出了一种用于循环平稳信号分析的偏相干方法,该方法可以有效实现多声源循环平稳声场的声场分离。随后Wan 等[88]以交流电机为对象,在消声室进行了实验验证。
表1 总结了基于声学传播方程的声源可视化重建方法的基本原理及适用范围。
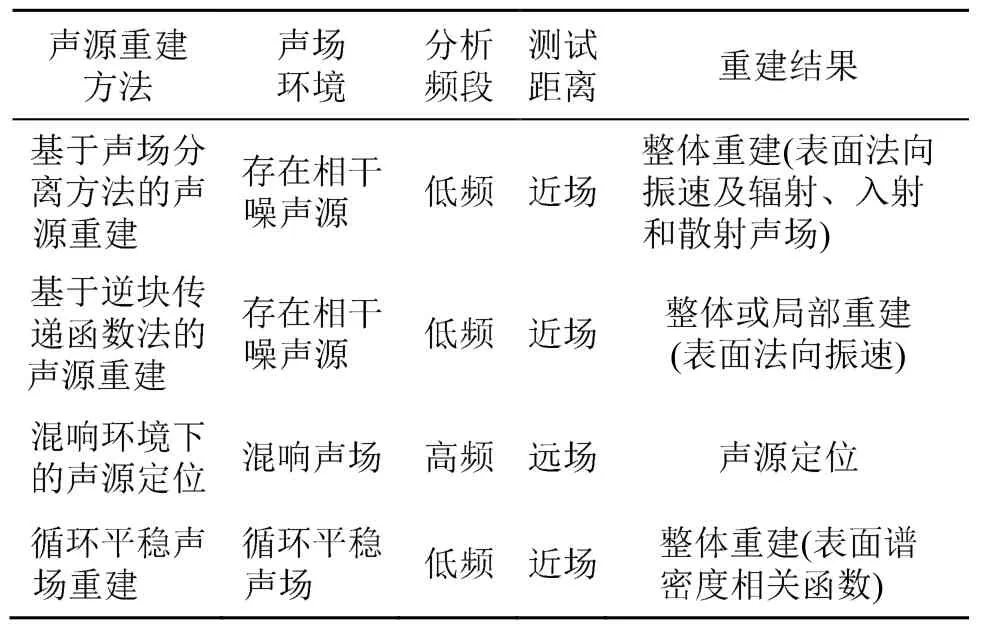
表1 基于声学传播方程的声源可视化重建的基本原理及 适用范围 Table 1 Basic principle and application of visual reconstruct-tion of acoustic sources based on acoustic propaga-tion equation
2 基于信号处理的噪声分离方法
声学测试采集的信号中可能会存在背景噪声以及测量误差等,为了实现声源精确重建,需要首先分离信号和噪声。分离方法主要包括基于子空间的方法以及基于信号噪声的不同结构的分离等。
2.1 基于子空间的方法
基于子空间方法的基本原理是根据互谱矩阵的奇异值分解构建信号和噪声子空间。多重信号分类(Multiple Signal Classification,MUSIC)算法[89]是一种常用的子空间方法,该方法假设信号与噪声不相关,通过将噪声子空间对应的特征值置为零进行信号降噪。在此基础上,Wax 等[90]通过赤池信息准则(Akaike Information Criterion,AIC)或最小描述长度(Minimum Description Length,MDL)准则来确定信号中声源的数目。随后,各种准则被提出用于确定声源数目,如修正AIC(corrected AIC,AICc)[91]、贝叶斯信息准则(Bayesian Information Criterion,BIC)[92]、Kullback 矢量校正信息准则(Vector Corrected Kullback Information Criterion,KICvc)[93]和加权信息准则(Weighted-Average Information Criterion,WIC)[94]等。Chen 等[95]比较了AIC、BIC、AICc、KICvc、和WIC 等准则在MUSIC 方法确定声源数目时的性能。余亮等[96]提出了(Stein Unbiased Risk Estimation,SURE)收缩与最优收缩准则,并且证明这两种准则可以进一步去除存在于信号子空间中的噪声。
2.2 基于信号噪声不同特性的方法
基于信号与干扰噪声不同特性,例如波数域分布特性的差异,或者信号和干扰噪声的低秩和稀疏特性等。在基于空间Fourier 变换的NAH 方法中,高波数的倏逝波很可能会被噪声淹没,导致声源重建结果误差剧增,因此需要波数域低通滤波[97]。Arguillat 等[98]根据湍流边界层噪声对应于高波数区域进行低通滤波,实现降噪处理。Gao 等[99]根据互谱矩阵中声源低秩和背景噪声稀疏的特性实现了信号和噪声的分离,该方法不仅适用于不相干的背景噪声分离,还适用于强干扰环境下的部分相干背景噪声分离。Yu 等[100]还根据信号和噪声具有不同的统计特性,设计了一种反向循环维纳滤波器,能够从包含平稳噪声源或者具有不同循环频率的循环平稳声源中提取出目标频率的循环平稳声源。
3 强干扰环境下声源重建研究展望
经过约30 年的不断发展,强干扰环境下的声源重建理论和技术已经取得了丰富的成果,并得到日益广泛的工程应用。但是仍然存在一些问题有待解决:
(1)逆块传递函数法假设声源表面的法向阻抗远远大于传播媒质的阻抗,即入射声和散射声不能影响声源表面的振动。但是对于气动噪声源、水下板壳辐射声源等,该假设通常不成立。因此,阻抗边界条件下的逆块传递函数法,是值得深入研究的课题。
(2)根据镜像源方法可以建立房间内声源和接收点之间的传递函数,该方法仅适用于矩形房间。对于不规则房间或者房间内有其他散射体的情况,如能建立房间内的脉冲响应函数,将有力地推动混响环境下声源重建的工程应用。
(3)相干噪声源存在时的波束形成算法。波束形成算法基于单极子假设,相干噪声源存在时无法准确实现声源反演。
