超声导波混频表征和定位早期局部损伤的研究进展
2022-07-29孙茂循项延训邓明晰
孙茂循,项延训,肖 飚,邓明晰
(1.上海理工大学机械工程学院,上海 200093;2.华东理工大学机械与动力工程学院,上海 200237;3.上海市特种设备监督检验技术研究院,上海 200062;4.重庆大学航空航天学院,重庆 400044)
0 引言
超声导波检测相较于超声体波的逐点式扫描,可以快速、有效地大范围扫描被测构件[1]。另外,超声导波的发射换能器和接收换能器可布置在被测件的同一侧,用于检测位于水中、地下、水泥浇灌结构中的构件或者带有涂层、保温层的构件,弥补了超声体波检测的不足[2]。传统超声导波可用于检测如宏观裂纹等尺寸与波长相近的损伤[3],但对疲劳、蠕变、塑性变形、微裂纹等无明显声反射界面的变化不敏感[2]。出现宏观裂纹后构件的剩余服役寿命通常十分短暂,不利于设备的维护和保养[4-5]。再者,构件中关键位置的损伤将会加速设备的整体失效。因此,对构件中关键位置的早期损伤的检测和维护显得尤为重要。与传统的超声导波相比,非线性超声导波主要研究频率与基频不同的高阶谐波,对尺寸远小于波长的缺陷或损伤比较敏感[6-7]。其中,位错、析出相、微裂纹或微孔洞等微观组织演化对高阶谐波的幅值有明显的影响,但对基波的影响较小[8]。因此,非线性超声导波因为具有远距离传输和感知微观组织演化的特性,近几十年来逐渐引起学者们的兴趣[9]。
超声导波中二次谐波的应用较为广泛,其中具有累积性的二次谐波与传播距离呈线性增长关系,因其对微观组织的演化更加敏感而备受关注[10-12]。目前,使用较为广泛的非线性超声导波包括非线性瑞利波和非线性兰姆波。本文根据激发具有累积效应二次谐波的难易程度进行回顾。其中,非线性瑞利波的能量主要集中在介质的表面,并随深度的增加而逐渐衰减,对表面损伤比较敏感。因为瑞利波的非频散的特性,非线性瑞利波中基波和二次谐波的相速度和群速度完全相等,即满足相速度和群速度匹配准则,较易产生具有累积效应的二次谐波[13-14]。目前,非线性瑞利波已被用于检测高温镍基合金中的塑性变形和低周疲劳[15]、AZ31 镁合金中涂层的早期损伤[16]、A36 钢中的疲劳损伤[17]、碳钢中的应力腐蚀裂纹[18]、17-4PH 不锈钢中的热老化[19]、钛合金中的塑性变形[20]、弯曲混凝土中的表面裂纹[21]和6061-T6 铝合金中的微裂纹[22]等。由于兰姆波具有频散性和多模式性,非线性兰姆波相较于非线性瑞利波较难产生具有累积效应的二次谐波。Deng[23-24]和de Lima 等[25]指出非线性兰姆波产生具有累积效应的二次谐波,需要同时满足相速度匹配和非零能量流准则。非零能量流准则可以理解为反对称模式或对称模式的基波仅能产生对称模式的二次谐波。Pruell 等[26-27]指出群速度匹配也是产生具有累积性二次谐波的必要条件。其中,S1-S2,S2-S4,A2-S4模式对(如S1-S2模式对表示S1模式的基波生成S2模式的二次谐波,其他模式对类似)使用较为普遍,已被用于量化评估铝板的拉-拉疲劳[28-29]、铝板中微裂纹的尺寸和方向[10]、1100-H14 铝合金中的塑性变形和疲劳损伤[26-27]、2024-T4 铝合金板中高速冲击引起的点蚀损伤[30]、6061 铝合金板中的疲劳裂纹[31-32]、复合材料中的热疲劳[33]、钢板中的微裂纹[34]、不同回火温度下改良9Cr–1Mo 钢[35]和改良9Cr–1Mo 钢的蠕变损伤[36]等。Xiang 等[37-39]利用非线性兰姆波表征高温下金属材料的力学性能退化,并关联声学非线性参量与微观组织演化。另外,近似相速度匹配的S0模式由于较易激发、模式单纯、后期数据较易处理等优点,逐渐引起学者们的兴趣。Zuo 等[40]、Wan 等[41]和Ding 等[42]指出在一定距离内,低频S0模式的二次谐波幅值与传播距离呈近似线性增长关系,可以用于检测材料中的微观组织演化。Sun 等[43]、Liu 等[44]、Zhao 等[45]和Mori 等[46]从理论分析或数值模拟的视角研究了声学非线性参数与塑性变形、微裂纹和接头缺陷的关系。但是测量系统和材料的非线性,例如设备的非线性、耦合剂的非线性,都将产生二次谐波,影响二次谐波来源的判断。另外,测量的二次谐波为发射换能器和接收换能器之间介质声学非线性的平均值,无法对指定区域的非线性进行评估[47]。
超声导波混频在频率、模式和传播方向等选择上具有一定的灵活性,可以解决上述问题[48]。de Lima 等[25]和Chillara 等[49]对超声导波同向混频给出有效共振发生的条件,即相匹配和非零能量流准则。Li 等[50]将上述理论进一步推广到三阶谐波的同向混频中,并设计实验进行验证。Hasanian 等[51-52]和Ishii 等[53]首次将矢量分析应用到任意方向的导波混频中,进一步解释超声导波混频的机理。超声导波的同向混频和相向混频在理论分析、数值模拟、实验验证和损伤检测方面取得了一定的进展[25,48-51,53,54-64]。但是,超声导波的非共线混频的研究目前主要集中在理论和模拟层面[52,65-66],相关实验验证和损伤检测报道较少[67]。
1 超声导波混频理论
Deng 等[24,50]利用二阶微扰近似和正交模式展开法,首次研究超声导波的二次谐波,并将上述理论推广至超声导波混频中,研究超声导波混频产生的二阶谐波(包括差频谐波、和频谐波和二次谐波)和三阶谐波。本文仅展示导波混频中二阶谐波的推导过程。非线性兰姆波的运动方程可以写为

薄板的表面应力为:

其中:σ,f,u分别为第一Piola-Kirchhoff 应力,体力向量和质点位移向量,ny是与y轴平行的单位向量。其中,第一Piola-Kirchhoff 应力σ由线性项σL和非线性项σNL组成:

假设二阶谐波的位移远小于基波的位移。根据二阶微扰法,总位移场可以表示为

式(6)可以理解为表面自由的薄板的求解问题。而式(7)可以理解为表面受载的薄板的求解问题。
Auld[68]的互易性关系(reciprocity relation)指出,利用正交模式展开法可以求解式(7),差频谐波或和频谐波的位移场为频率等于差频或和频的一系列m阶的传播模式的组合:
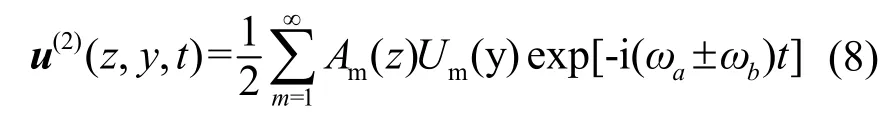
其中:ωa和ωb为基波的频率,Um(y)为m阶的传播模式的波结构。幅值Am(z)可由式(9)解得:

其中:ka和kb为基波a和b的波数。式(9)的解为

其中:Aa、Ab和A±为z=z0时表面处接收的基波a、基波b和差频谐波或和频谐波的幅值。
上述公式推导是基于连续波的同向混频,未考虑群速度和传播方向的影响。Jones 等[69]将矢量分析应用于超声体波混频中,提出了5 种超声体波混频的模式。Hasanian 等[51]首次将矢量分析应用到任意方向的超声导波混频中,并利用水平剪切波SH0模式的相向混频,从模拟和实验层面,验证了矢量分析在超声导波相向混频中的可行性。根据矢量运算可知,超声导波混频中波数之间的关系为

其中:k±为差频谐波或和频谐波的波数,α为两基波的夹角。
超声导波混频可以评估混叠区内材料力学性能的退化,通过改变基波的激发时间以扫描被测试样,确定被测试样中损伤的空间分布。因此,定位的精度与混叠区的尺寸密切相关。Sun 等[62]基于超声导波的相向混频,指出定位的精度Rslt取决于基波的频率、相速度、群速度和周期数,表达式为

Sun 等[62]将时域信号分析法应用于超声导波混频中,研究混叠区内外和频谐波的幅值和时域长度的变化情况。其中,和频谐波的时域长度与传播距离的关系为
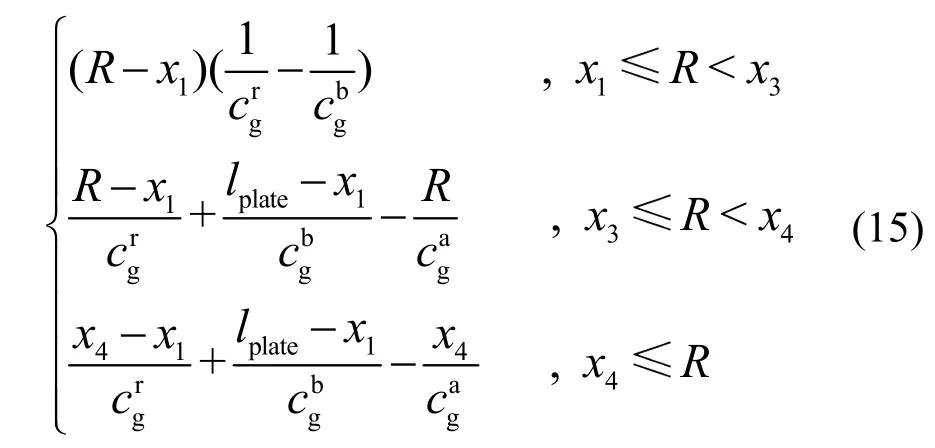
其中:lplate为薄板的长度,R为接收换能器的位置,为和频谐波的群速度。首先,基波a 和b 的前端在x=x3处接触,其中x表示距薄板左端的距离。然后,基波a 的前端与基波b 的后端于x=x4处接触。最后,基波a 的后端与基波b 的前端于x=x1处接触。Chen 等[63]基于有限元仿真将兰姆波的相向混频推广至双层板中。上述方法也可以应用到其他形式的超声导波混频中,具有一定的适用性。
2 超声导波混频
根据超声导波交汇的方式,超声导波混频可以分为同向混频、相向混频和非共线混频。超声导波的同向混频中基波的传播方向相同,未涉及交汇的角度,de Lima 等[25]早在2003 年就已提出较为完善的理论。之后,上述理论也经过后续模拟和实验的验证,已用于表征微观组织演化。但是,超声导波的同向混频混叠区较大,不利于局部损伤或缺陷的定位。超声导波的相向混频和非共线混频中基波的传播方向呈一定角度,可以克服上述缺点。但是,同向混频的理论不完全适用于超声导波的相向混频和非共线混频。相关研究发展较为缓慢,直到2017 年Lissenden 课题组才开展较为完善的理论、模拟和实验研究[51-52,54,64],后续又跟进了一些模拟和试验报道[67]。本文根据超声导波混频发展的时间脉络,依次回顾不同类型超声导波混频的发展状况。
2.1 超声导波的同向混频
Shan等[54]利用SH0模式的混频产生具有累积效应的S0模式,以表征2024-T6 铝板中的疲劳损伤。图1 为当铝板疲劳寿命达到0、25%、50%、75%时,作差信号的幅值与传播距离的关系[54]。差频信号的幅值与传播距离在不同被疲劳寿命时的拟合关系为:0 时,y=0.001 855x+0.108 7 ;25% 时,y=0.002 338x+0.102;50%时,y=0.002 397x+0.106 4;75%时,y=0.002 692x+0.095 16。由图1 可知,当疲劳寿命达到75%时,斜率增加了45%。如图2 所示,误差远小于斜率的增幅,说明实验测量中材料非线性所引起的变化远大于系统非线性所引起的变化。

图1 当铝板疲劳寿命达到0、25%、50%、75%时,作差 信号的幅值与传播距离的关系[54] Fig.1 Amplitude Aab of the difference signal versus propagation distance for aluminum plates cycled to 0,25%,50%,and 75% of the fatigue life[54]

图2 四个试样中,作差信号幅值的归一化斜率与 疲劳寿命的关系[54] Fig.2 Normalized slope of the amplitude of difference signals versus the fatigue life for the four samples[54]
Jiao 等[55]利用S0模式的同向混频产生的和频谐波表征钢板中微裂纹。有限元仿真中微裂纹尺寸对声学非线性参数的影响[55]如图3 所示。图3(a)中,声学非线性参数与微裂纹长度之间呈单调递增的关系。其中,声学非线性参数对微裂纹长度为1.1~1.5 mm 的微裂纹更加敏感。图3(b)中,有限元仿真中声学非线性参数与微裂纹宽度呈单调递减的关 系。当宽度小于20 μm 时,声学非线性参数对微裂纹更加敏感。实验测量中也观察到相似的结果,如图4 所示。

图3 有限元仿真中微裂纹尺寸对声学非线性参数的影响[55] Fig.3 Influence of micro-crack size on acoustic nonlinearity parameters in finite element simulations [55]
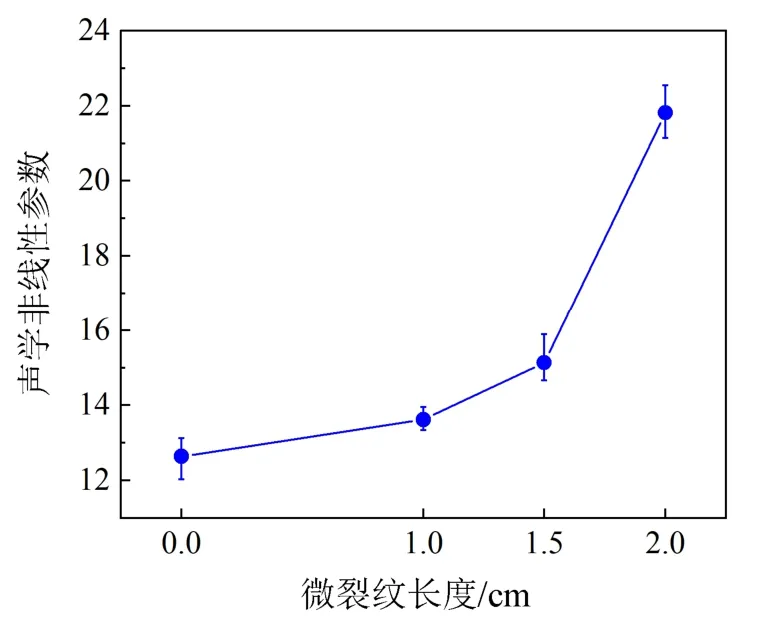
图4 实验中声学非线性参数与微裂纹长度的关系[55]Fig.4 The measured acoustic nonlinearity parameter versus the length of micro-cracks in experiment[55]
Li 等[56]利用S1模式的同向混频表征复合多层板的冲击损伤。混频峰值随冲击能量的变化趋势[56]如图5 所示。混频峰值的计算值与试样中施加的冲击能量成正比。上述方法主要利用混频中的和频谐波,有效地避开测量系统的非线性干扰,但仍无法定位板中的材料损伤。

图5 混频峰值随冲击能量的变化趋势[56]Fig.5 Relationship of the mixing frequency peak value and impact energy[56]
Metya 等[57]利用S0模式的混频评估改良9Cr-1Mo钢蠕变期间的局部变形。不同中断时间t及相应蠕变应变S时的归一化Aω1+ω2与位置的关系[57]如图6所示。归一化Aω1+ω2在100 h 前变化较小,200 h 后当蠕变应变达到1.8% 时开始增加,其中位置2 和3处的归一化Aω1+ω2增长更快。另外,试样失效的位置恰好位于试样失效前归一化Aω1+ω2最大的位置[57]。

图6 不同中断时间及相应蠕变应变时的归一化Aω1+ω2 与位置 的关系(插入图片为440.5 h 后失效的试样)[57] Fig.6 Normalized Aω1+ω2 (evaluated from wave mixing) along the gage length and interruption time versus corresponding creep strain;inset:a view of the failed specimen after 440.5 h [57]
Li 等[58]和Ding 等[59]将体波One-way Mixing 理论推广至低频超声导波混频中。Ding 等[59]基于有限元仿真,利用S0和A0模式的同向混频产生的反向传播的A0模式定位铝板的微裂纹区。Sun 等[60]提出 超声导波中One-way mixing 的普适性共振条件。基于有限元仿真验证上述理论,上述方法用于定位薄板中局部损伤,相关结果如图7 所示。Li 等[61]从理论和仿真的层面研究了管中超声导波的One-way mixing 现象。超声导波的One-way mixing 可以在同一区域发射或接收超声信号,甚至可以通过双工器的辅助,实现同一探头发射和接收超声信号,具有良好的应用前景[66]。

图7 共振波的归一化幅值与混叠区位置的关系[60]Fig.7 Normalized amplitude of the resonant mixed wave versus location of the mixing zone[60]
2.2 超声导波的相向混频
磁致伸缩换能器(Magnetostrictive Transducer,MST)产生的0.31 MHz 和1.7 MHz 的SH0模式的相向混频产生2.01 MHz 的S0模式将用于表征7075-0铝合金的热损伤[51]。换能器的布置如图8 所示,混叠区 1 和混叠区2 分别位于局部热损伤区内外。其 中,铝板的局部热老化是经过加热到327℃再冷却3 h 后制得。由图9 可知,加热前后区域1 和区域2的作差信号的比值均小于1,说明S0模式在混叠区外不具有累积效应。另外,热老化后微观组织演化引起上述比值的显著增加。

图8 定位热老化的测试装置:热损伤区的尺寸和位置[51]Fig.8 Test equipme nt for localized heating:size and location of mixing zone and heated region[51]

图9 热老化前后区域1 和区域2 的作差信号的比值[51]Fig.9 Difference signals received in zone 1 normalized with difference signals received in zone 2[51]
Cho 等[64]利用聚偏氟乙烯(Polyvinylidene fluoride)换能器接收相向混频产生的S0模式的和频谐波,以检测1 mm 厚的2024-T3 铝合金板中的高周疲劳。实验中的缺口试样如图10(a)中虚线所示,其疲劳损伤主要集中在缺口位置。通过机加工切割出如图10 所示测量试样。

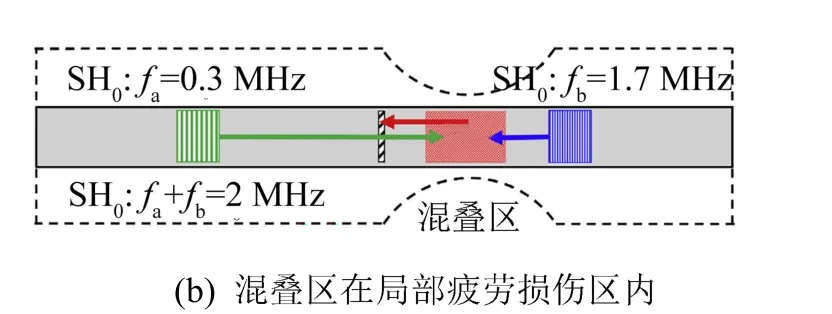
图10 定位局部疲劳损伤的波束混频的装置[64]Fig.10 Schematic of wave mixing test equipment to detect the localized fatigue damage[64]
如图11(a)所示,原始试样中存在6 个不同的、相互重叠的混叠区。原始试样中混叠区的幅值比Aab/(AaAb)的平均值为2.10 V-1。疲劳试样的测量结果如图11(b)所示,疲劳损伤区外混叠区的幅值比Aab/(AaAb)的平均值为2.27 V-1,而疲劳损伤区内混叠区的幅值比Aab/(AaAb)的平均值为3.56 V-1。该测量结果说明上述扫描方法可以表征和定位板中的局部疲劳损伤。

图11 Aab/(AaAb) 与混频区位置的关系[64]Fig.11 Bar graphs showing Aab/(AaAb) vs.the location of mixing zone in the plates[64]
2.3 超声导波的非共线混频
Blanloeuil 等[67]基于接触声学非线性(Contact acoustic nonlinearity)模型研究了SH0模式的非共线混频,在实验中观测到S0模式的和频谐波,指出利用此方法的应用前景(即测量裂纹类缺陷或界面的接触声学非线性)。Hasanian 等[52]基于有限元仿真验证非共线混频的模式对,即频率为 0.78 和1.5 MHz 的SH0模式成90º混频可产生频率为2.28 MHz 的S0模式,评估基波到二阶谐波的传输效率,统一导波混频与体波混频的理论公式。Hasanian 等[52]还提出简化解析模型分析有限尺寸混叠区的影响,发现二阶谐波的幅值与混叠区尺寸相关,指出群速度不匹配并不影响基波到二阶谐波的能量传输。Ishii 等[65]利用有限元仿真研究低阶反对称模式的瑞利-兰姆波混频,指出共振波的幅值不仅取决于基波的频率、幅值、交汇角,还取决于模式对的选择,与基波到共振波的能量传递效率相关。Lv 等[66]采用有限元仿真研究A0模式的非共线混频,用于表征微裂纹的尺寸和方向。S0R的传播方向随微裂纹的倾斜角线性增长,相关增幅是微裂纹倾斜角增幅的两倍,S0T的传播方向未受微裂纹倾斜角的影响,如图12 所示。同时S0T和S0R的幅值与微裂纹宽度呈线性递减关系。因此,S0T可用于测量微裂纹的尺寸,S0R可用于辨识微裂纹的方向。另外,Lv 等[66]指出A0模式混频与微裂纹作用的物理机制和横波混频与微裂纹作用的物理机制相似。
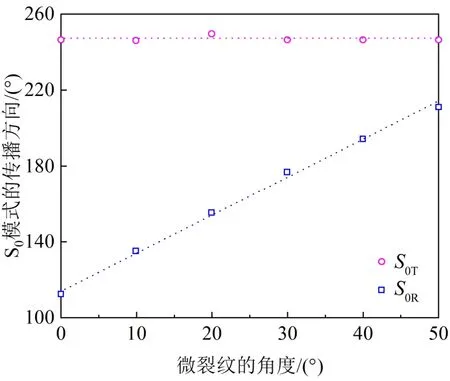
图12 S0R 和S0T 的传播方向与微裂纹方向的关系[66] Fig.12 Propagation direction angles of generated S0R and S0T waves for cracks with different orientations[66]
2.4 小 结
群速度相等或相差较小的导波同向混频,混叠区相对较大,不利于板中局部损伤的精确定位,但能产生能量较大的差频谐波或和频谐波,对板中微观组织的演化比较敏感。超声导波相向混频的混叠区较小,可以排除测量系统的非线性干扰,利于板中局部损伤的精确定位。超声导波的非共线混频在频率、模式、传播方向等的选择上具有一定的灵活性,同时存在较难激发的问题。
3 结论
超声导波混频在理论方面的研究已较为完善。从连续波的同向混频产生具有累积效应的差频谐波或和频谐波,到相向混频和非共线混频中矢量分析的运用,在公式推导上都取得了一定的进展。
超声导波混频在有限元模拟方面的研究也趋于成熟。数值仿真基于三阶弹性常数(Third-order elastic constants)模型研究基波在连续介质中交汇产生具有累积效应的差频谐波或和频谐波。数值仿真还基于接触声学非线性(Contact acoustic nonlinearity)模型,研究基波与微裂纹交汇产生的差频谐波或和频谐波。
在实验验证方面,超声导波的同向混频由于基波与差频谐波或和频谐波的传播方向一致,易于激发而报道较多。超声导波的相向混频中,两束基波的传播方向相反,混叠区尺寸较小且差频谐波或和频谐波能量较小,激发相对困难,因而报道较少。超声导波的非共线混频中,基波与二阶谐波的频率、模式、传播方向等需同时满足共振条件才能产生具有累积效应的差频谐波或和频谐波,因此非共线混频的激发较为困难而报道较少。
在无损检测方面,超声导波的同向混频已被用于评估金属材料中处于早期阶段的微裂纹、低周疲劳、冲击损伤、蠕变中的局部变形等;超声导波的相向混频也被用于表征和定位早期阶段的热老化、高周疲劳等;超声导波的非共线混频的应用还有待进一步研究。对于金属板中塑性变形和低周疲劳,无论是超声导波的二次谐波还是超声导波混频,声学非线性参数与塑性应变或疲劳寿命率均呈单调增加的关系,其中在塑性变形和低周疲劳的早期增加较快,后期逐渐趋于平缓;对于金属板中的微裂纹,无论是超声导波的二次谐波还是超声导波混频,声学非线性参数与微裂纹长度或宽度均呈单调变化的关系。另外,当声波传播方向与裂纹长度方向垂直时,声学非线性参数对微裂纹最敏感。
超声导波混频的应用仍面临着许多挑战。首先,目前超声导波混频的研究主要涉及低频段水平剪切波和兰姆波的混频(如SH0、S0、A0模态),复杂的高频段水平剪切波和兰姆波的混频仍有待进一步的探索。再者,实验测量中兰姆波相向混频或者非共线混频生成的差频谐波或和频谐波的传播性仍有待进一步验证。在低频段水平剪切波同向混频、相向混频和非共线混频的实验中,研究者已经测出了能够传播的差频谐波或和频谐波。另外,低频段兰姆波同向混频生成的差频谐波或和频谐波的传播特性也得到了证明。但对于兰姆波相向混频或者非共线混频,差频谐波或和频谐波传播性的相关报道仍然较少。作者认为出现上述问题的原因可能是,筛选模式组中基波到二阶谐波的能量传递效率太低,所以差频谐波或和频谐波的信号较弱。最后,差频谐波或和频谐波能定位及表征的损伤类型有待进一步增加。
综上所述,超声导波混频可以表征和定位板状或管状结构中的早期局部损伤,是一种新兴的结构健康检测或监测方法,具有良好的工程应用前景。
