闸门有限元静力计算及振动特性分析

2022-07-29薛海朋黄叶雯

江苏水利 2022年7期

蒋涛，薛海朋，刘斌，黄叶雯

（1.江苏省骆运水利工程管理处，江苏宿迁 223899；2.江苏省秦淮河水利工程管理处，江苏南京 210022；3.河海大学能源与电气学院，江苏南京 211100）

水工建筑物包含了众多物件，而闸门是其中非常重要的组成部分，对水利工程来说十分关键［1］。当闸门闭合开启时，可以通过其角度的改变来调节上下游水位和流量，可以用来挡水、泄水，还可用在防洪、灌溉、航运等多方面。按照水闸的作用划分为进水闸、节制闸、冲沙闸等，按照闸室结构划分为2种，包括开敞式和涵洞式水闸［2］。水工建筑物的进出口位置是水闸所在处，闸门通过开启闭合来保障其运行以及安全。实际运行中闸门在挡水的过程中，水流内部的脉动压力作用在闸门上，会使得闸门发生振动，这与闸门的固有特性和外部激励载荷有很大的联系，倘若振动剧烈，对整个枢纽工程的安全稳定运行有严重的影响［3］，所以研究闸门自身结构的的自振特性对实际水利工程的安全稳定具有重要的意义［4］。

2016年，受连续强降雨、多次台风等因素影响，秦淮河流域水位持续走高。10月秦淮河流域又发生了严重秋汛，汛后检查发现，秦淮新河闸在汛期和秋汛期间长时间行洪，下游河道局部冲刷和右岸砌石护坡小部分坍塌，管理处随即对该段堤防附近水域进行了水下检查。检查结果表明，该段水下河道断面存在一定冲刷，河底高程较河道标准断面低，经分析与闸下流态有一定影响。因此，本文针对秦淮新河的实际问题来研究闸门的振动问题，对闸门进行有限元静力计算以及模态分析，寻求闸门振动频率的规律和振动的响应关系，对减轻甚至避免振动的发生以及保证闸门的安全运行有重要作用。

1 闸门有限元计算

1.1 闸门结构形式

本文针对秦淮新河水利枢纽节制闸进行研究分析。该闸门为平面钢闸门，共12扇，门叶材料采用Q235，焊条采用E4303，闸门吊头利用原下扉门吊头，然后吊头底板用螺栓连接到其底座上。门叶上布置了4道实腹式主梁，6道纵梁，边梁两边各1个，而边梁的内外腹板之间是主轮所在之处，门叶采用下游止水。吊点间距为5.19 m，中间3根梁为16＃b型槽钢，闸门构件的材料为Q235钢，Q235在厚度小于等于16 mm时的弹性模量为2.06×105MPa，泊松比为0.3，密度为7 850 kg/m3。根据《水利水电工程钢闸门设计规范》（SL74—2019），闸门的抗拉、抗压和抗弯强度均为160 MPa。

1.2 闸门有限元静力计算

1.2.1 闸门模型建立

平面钢闸门实际结构较为复杂，故在UG建模软件中将其简化，如图1所示，后导入计算软件ANSYS。将2个软件中的模型进行对比观察，保证模型的完整及可靠。

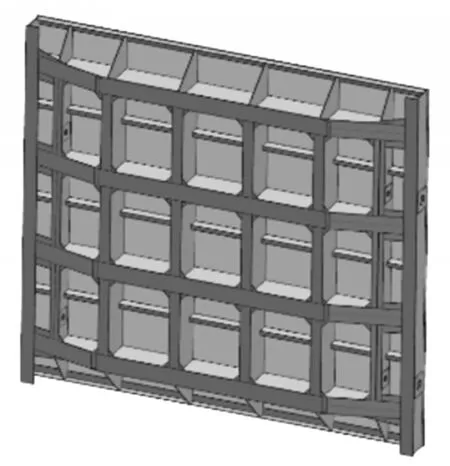
图1 闸门简化三维模型

平时运行中，上游的水压通过比较大，所以平面钢闸门的门体结构在一定程度上会发生弯曲、扭转、拉压、剪切等共同作用下的变形。为了更真实地模拟出闸门在实际运行中的工作状态，将闸门结构设置为板、壳、梁等的组合结构体，同时将型钢设置为板壳单元，它在闸门中主要起到联结作用。当闸门受到水流载荷的影响时，各面板、主副梁板等部位都会发生微小的变形，本文主副梁板则选取适宜分析中等厚度的SHELL 181单元作为壳体单元，其特点是能够承受大变形与扭转，2种类型的横梁选取beam189单元，整体网格划分见图2所示。

图2 闸门有限元模型

1.2.2 边界条件及结果分析

闸门整体方向设定为：x方向即闸门的跨度，y方向即闸门的高度，z方向即上下游水流流向，而面板底部中心即为坐标原点的位置。

边界条件：z方向门槽约束左右滚轮，主梁板在x方向上限制变形，即受到约束，闸门底部在y方向上也受到约束。迎水面面板受到静水压力的作用，重力加速度即9.81 m/s2，流体密度即为水的密度。

将闸门4个主横梁由上到下依次编号为1＃主横梁、2＃主横梁、3＃主横梁、4＃主横梁，纵梁板从左到右编号1＃～6＃。本文中所说的最大、最小应力以及应力分布图均为Von mises stress等效应力。

（1）主横梁

主横梁的最大剪应力、最大等效应力列于表1中。

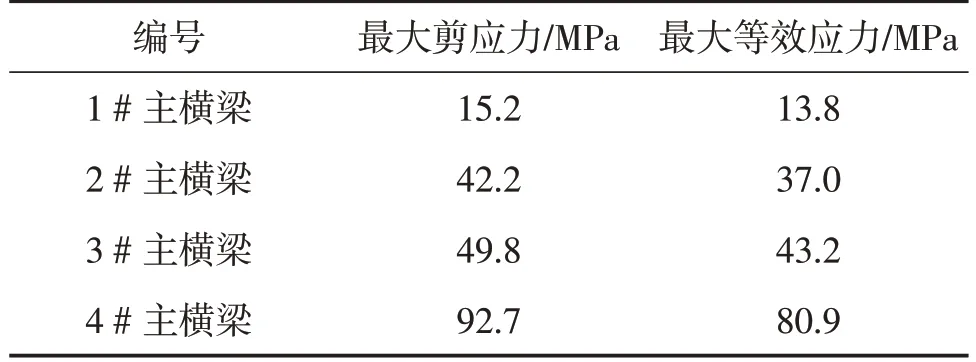
表1 闸门主横梁最大剪应力、最大等效应力

整个闸门的最大应力出现在右边柱上，最大应力为90.7 MPa；1#主横梁、2#主横梁、3#主横梁最大应力均在左边缘处，最大应力值分别为13.2 MPa、37.0 MPa、43.2 MPa。4＃主横梁最大应力在右边缘处，最大应力值为80.9 MPa；4个主横梁的最小应力均在中心处，且应力值从上到下越来越大，4#主横梁所受的应力最大。

（2）纵梁

由纵梁应力分布可知：最大应力出现在5#纵梁板上，最大应力值为18.5 MPa，最小应力出现在6#纵梁板上。纵梁板的应力值与主梁板相比较小，闸门大部分的应力都集中在主梁板上，同时每个纵梁板应力分布基本一致。

（3）边柱与面板

由边柱应力分布可以看出，左右边柱应力分布基本对称，最大应力在右边柱与4#主横梁相连接的地方，数值为90.7 MPa。最大应力在与4#主横梁相连接的附近，最大应力值为54.6 MPa。整体呈对称分布，从上到下应力值越来越大，大应力集中在面板底部。

（4）闸门刚度

闸门最大的变形为5.3 mm，出现在面板底部，作为闸门的主要受弯构件，4个主横梁的最大挠度从上到下分别为0.9 mm、1.7 mm、2.6 mm、3.6 mm。

2 闸门模态分析

2.1 模态分析基本原理

模态分析是进行动态分析的前提和基础，对于解决复杂结构的振动问题是非常有效的分析手段。对系统方程特征值和特征向量进行不同程度的求解，就能够得出其固有频率，而与此相匹配的振型也能显示出来。闸门在运行时分别要考虑两种状态，分别为干模态和湿模态分析，对两种情况都要进行分析。

闸门无水状态下，结构系统内部的运动微分方程为

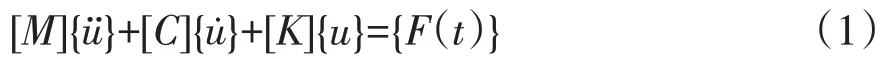
式中：[M]为质量矩阵，[C]为阻尼矩阵，[K]为刚度矩阵，{̈}为节点加速度列向量，{̇}为节点速度列向量，{u}为节点位移列向量，{F}为激励载荷向量。

没有阻尼时，其运动方程表示为

在某一初始条件下，系统按某一频率做简谐运动，其位移情况为

对式（3）求导后带入到式（2）可得：

则系统的特征方程为

当闸门中有了水流作用时，此时两者之间就会发生耦合，这就会影响闸门自身的振动特性。所以闸门振动方程需要考虑到水体所带来的的影响，通常选择质量矩阵中增加附加质量，以此可以模拟闸门在受到水流作用时的实际状态。此时结构系统的运动微分方程［5］又可以表示为

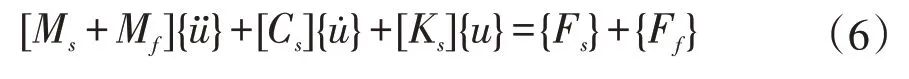
式中：[Ms]为质量矩阵，[Cs]为阻尼矩阵，[Ks]为刚度矩阵，[Mf]为水流作用的附加质量矩阵，[Ff]为水流引起的载荷向量，[Fs]为闸门结构上的其他载荷向量。

所以最终得到的闸门系统特征方程为

ANSYS软件采用非对称法来提取结果，该种方法能够有效解决质量矩阵与刚度为非对称的相关问题。分析步骤即为先进行干模态分析，再对闸门进行湿模态分析。在计算过程中所获取的结果呈现无限多阶的模态［5］，而对于实际工程并不要运用到所有的数据，只有前几阶具有参考价值，故本文仅提取了平面钢闸门在两种状态下的前八阶模态用以分析对比。

2.2 干模态分析

干模态即无水状态时，对闸门进行计算可知，一阶振型明显振幅偏小，而二阶振型中闸门开始发生变形，集中表现为上半部分向顺水方向发生一定程度的弯曲，到了三阶振型变形方向不变，部位集中在了闸门下半部，四阶振型为闸门顶部x和z方向的变形弯曲，五到八阶振型的形式基本都为闸门内部梁系结构的振动。

2.3 湿模态分析

对闸门结构在有水状态下的振动特性进行计算，对其施加附加质量模拟闸门在动水中的运动形态。一阶振型时闸门整体上没有发生明显的变形，到了二阶振型时闸门上半部尤其是顶部出现了集中区，表明该处变形相对较大，整体向顺水方向弯曲，三阶振型时闸门的下半部开始发生变形，方向同样是顺水向，再往后到了四阶振型，其形式为闸门在z方向翻转扭曲，五阶振型的形式为闸门除中心部分向四周弯曲，六到八阶振型的形式都为闸门内部梁系结构的振动。

2.4 对比分析

将两种模态的振型进行对比可以发现，湿模态时前五阶振型基本上都是闸门外部上的整体变形振动，而干模态时只有前四阶保持这样的状态，剩余的均为内部梁系结构的振动，这就说明有水无水即水体的出现对闸门会产生一定的影响。表2为闸门有水无水前八阶振动频率对比，从表中可知闸门在湿模态时除个别数据外均比干模态固有频率低，到了高阶两者差距开始缩小，相差无几，而这些都表明水体的存在增大了闸门共振的机率。因为闸门在有水的情况下，如果产生振动会引起流场内部的流态变化，其会反作用于闸门本身对其造成影响，从而产生更强烈的振动，由此可以看出闸前有水时的耦合问题不容忽视。