基于三维激光扫描的吊索钢丝锈蚀形貌分析

马亚飞，白浩，苏小超，阳健，王磊，张建仁

（长沙理工大学 土木工程学院，湖南 长沙 410114）

桥梁腐蚀、损伤等病害在车辆反复荷载和外界不利环境作用下日益突出。已建的中下承式拱桥、悬索桥等大跨度桥梁吊索，长期处于高应力状态，若防护不当，吊索内高强钢丝易发生腐蚀[1-2]，会显著降低吊索的使用寿命。近年来，已发生多起因腐蚀导致的吊索安全事故，带来巨大的人身伤亡和财产损失。桥梁管理部门将腐蚀吊索及时更换，以防该类事故的发生。钢丝锈蚀分为均匀锈蚀和局部锈蚀，而局部锈蚀易引起钢丝局部应力集中，加速疲劳裂纹扩展，对结构性能更为不利。因此，研究钢丝的坑蚀特征，对研究其力学性能退化规律尤为重要。

目前，针对锈蚀导致结构性能退化的研究已有较多成果。NAKAMURA 等人[3-4]发现镀锌钢丝的伸长率和扭转强度均随锈蚀程度的增加而降低，待表面镀锌层完全锈蚀后，钢丝延性显著降低。李晓章等人[5-6]研究表明：高强钢丝极限应变的下降源于锈蚀钢丝横截面的不均匀损失，钢丝局部的微小锈坑成为裂纹萌生源。兰成明等人[7]建立了考虑腐蚀影响的三参数Weibull 模型，发现随着钢绞线腐蚀程度的增加，疲劳寿命迅速减小，指定疲劳寿命下的许用应力幅迅速降低。FURUYA 等人[8]通过自然环境腐蚀试验，指出高温和水分是拉索内钢丝腐蚀的主要诱因。张威等人[9-10]分析了蚀坑分布状况，认为蚀坑长度、宽度和深度均服从对数正态分布，蚀坑深宽比服从正态分布，而最大蚀坑深度服从极值Ⅱ型分布。ZHANG 等人[11]发现锈蚀平均截面积与最小截面积之比服从Gumbel极值分布，随着锈蚀的发展，其均值和均方差也随之增大。楼纪昂等人[12]通过ANSYS 仿真模拟，探讨高强钢丝蚀坑长度、宽度和深度等因素对应力集中系数的影响程度，发现最大影响因素为蚀坑长度，深度次之，宽度最小。蒋超等人[13]发现高强钢丝均匀腐蚀深度的变异系数随腐蚀时长减小，最大点蚀深度服从极值I 型分布，并建立了均匀腐蚀深度与最大点蚀深度的预测模型。然而，现有研究多采用通电加速腐蚀的方法获取锈蚀试件，这与自然环境存在较大差异，测试结果难以反映现实情况。而考察参数局限于最大腐蚀深度、宽度等，忽视了整体腐蚀的影响。因此，本研究以服役实桥上更换的吊索为研究对象，对其内部高强钢丝进行酸性盐雾试验模拟自然环境腐蚀，得到了质量损失率与锈蚀时间的变化规律。通过对锈蚀钢丝进行三维激光扫描（3D激光扫描），测得了不同位置的蚀坑深度。拟以点蚀系数表征局部锈蚀程度，考虑钢丝整体锈蚀的影响，经统计分析高强钢丝局部锈蚀参数的概率分布特征，以期为研究高强钢丝力学性能规律提供借鉴。

1 自然环境模拟锈蚀试验

1.1 试件制作

四川某桥是一座中承式混凝土拱桥，于2016年进行了吊索更换，拆除时吊索已服役14 a。该吊索由109根直径为7 mm的平行镀锌高强钢丝组成，钢丝抗拉强度标准值为1 670 MPa。拆除的部分吊索运回实验室，经切割加工后，得到60 根长度为400 mm的钢丝样本。

采用酸性盐雾试验，模拟自然环境对高强钢丝的腐蚀，样本分6 组，每组10 根，试验周期分别为15、30、60、90、120 和150 d。主要设备为CK/YW-60C 的盐雾腐蚀试验箱和ATC 系列笔式酸度计。电导率不超过20 μs/cm 的蒸馏水和50±5 g/L的化学纯氯化钠配制盐溶液，通过冰乙酸和化学纯氢氧化钠，控制溶液PH 值在3.0～3.1[14]。盐雾试验控制温度为25℃。在500 mL密度为1.19 g/mL的盐酸中，加入3.5 g六次甲基四胺和适量蒸馏水，配制成1 000 mL的除锈液。

先用丙酮擦拭试件表面，称重，放入试验箱，待试验周期结束时取出各组试件，自然风干30～60 min，用温度不高于40℃的清洁流动水冲洗钢丝表面，去除残留锈蚀液。

钢丝锈蚀后，外观如图1 所示。在图1 中，白色物质和红色物质分别为钢丝表面镀锌层和内芯基体的锈蚀产物。从图1 中可以看出，盐雾暴露15 d之后，钢丝表面镀锌层已开始锈蚀，基体内芯出现了局部点蚀，随着盐雾暴露天数的增加，腐蚀向钢丝基体内芯发展，腐蚀程度愈发严重，钢丝截面呈不规则变化。

图1 不同暴露时间下钢丝锈蚀形貌Fig.1 Corrosion morphology of steel wire after different exposure time

1.2 高强钢丝质量损失

先将钢丝表面烘干，在室温环境下用配置好的除锈液清洗试件10 min，用软毛刷轻轻擦拭试件，除去钢丝表面膨松的锈蚀物。再用清水将试件充分冲洗，烘干，冷却至室温，再次称重并记录。锈蚀高强钢丝清洗后的外观如图2所示。在锈蚀初始阶段，仅钢丝表面镀锌层发生锈蚀，部分腐蚀严重区域出现点蚀，钢丝表面出现微小蚀坑，钢丝截面直径未有明显变化，随着暴露时间的增加，钢丝表面点蚀加重，腐蚀产物覆盖整个试件表面，局部出现较大蚀坑，钢丝直径明显变小。

图2 除锈后钢丝样本Fig.2 Steel wire samples after derusting

经本试验配置的酸性盐雾加速锈蚀后，得到试件的质量锈蚀率见表1。

表1 钢丝质量损失Table 1 Mass loss of steel wires

钢丝质量损失率的计算式为：

钢丝平均质量损失率与盐雾环境暴露时间的变化关系如图3所示，经回归分析得：

式中：t为盐雾环境暴露时间，d；t0为短期酸性盐雾暴露环境下镀锌高强钢丝开始发生锈蚀所需的时间，d，本试验t0=15。

从图3可以看出，由于钢丝表面镀锌层先发生锈蚀，锈蚀是一个从无到有的过程。因此，初始质量损失速率较快，待到钢丝表面覆盖的锈蚀产物形成一道保护膜后，腐蚀速率趋缓，随着锈蚀程度进一步加剧，部分锈蚀产物脱落，钢丝再次暴露在盐雾环境中，锈蚀速率有所回升。

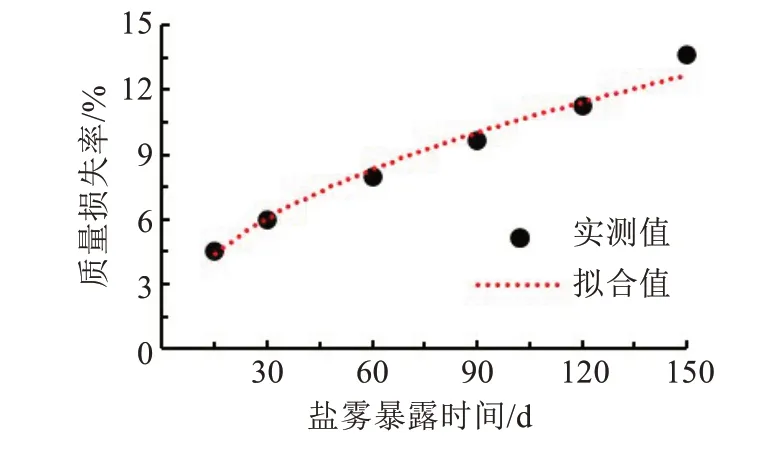
图3 平均质量损失率与盐雾暴露时间关系Fig.3 Relationship between average mass loss rate and salt spray exposure time

2 三维激光扫描

为研究高强钢丝的局部锈蚀特征，利用三维激光扫描技术测量钢丝表面的蚀坑特征。本试验采用仪器为精度0.02 mm 的FARO Laser Scan Arm3D 激光扫描测量仪。从6 组锈蚀试件中各取3根，共计18根样本，对其中间200 mm 区域进行扫描，经配准、简化、去噪等流程，得到原始点云数据。通过三维数据处理，删除多余点、点云数据封装、划分网格等流程，得到多边形钢丝网格模型。然后，沿钢丝轴向每隔2 mm 剖切1 个横断面，如图4所示。固定圆心，在坐标系中构建钢丝平均锈蚀深度圆截面和半径R0=3.5 mm 的原始圆截面，测得原始截面圆心到锈蚀钢丝表面最近点的距离s，通过计算得到钢丝表面蚀坑深度d，其计算式为：

图4 钢丝模型横截面截取Fig.4 Cross section interception of steel wire model

2.1 最大点蚀深度

不同盐雾暴露时间下，18 根钢丝表面最大点蚀深度纵向、轴向分布情况如图5 所示。从图5 可以看出，最大坑蚀深度沿钢丝轴向存在较大差异，相同盐雾暴露时间下同组钢丝最大坑蚀水平较接近。钢丝最大坑深随盐雾暴露时间的增长逐渐增大，如图5(g)所示，但纵坐标轴方向的波动范围逐渐变小，表明钢丝轴向腐蚀程度趋于均匀。

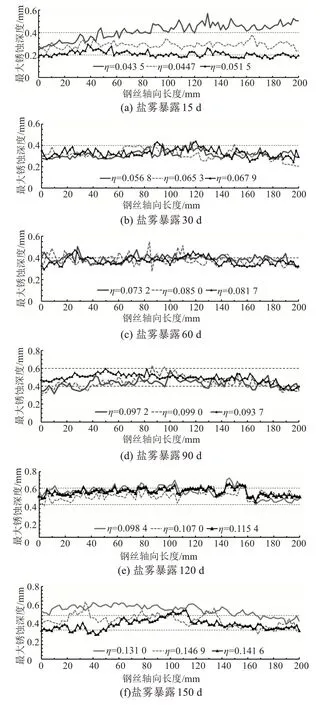
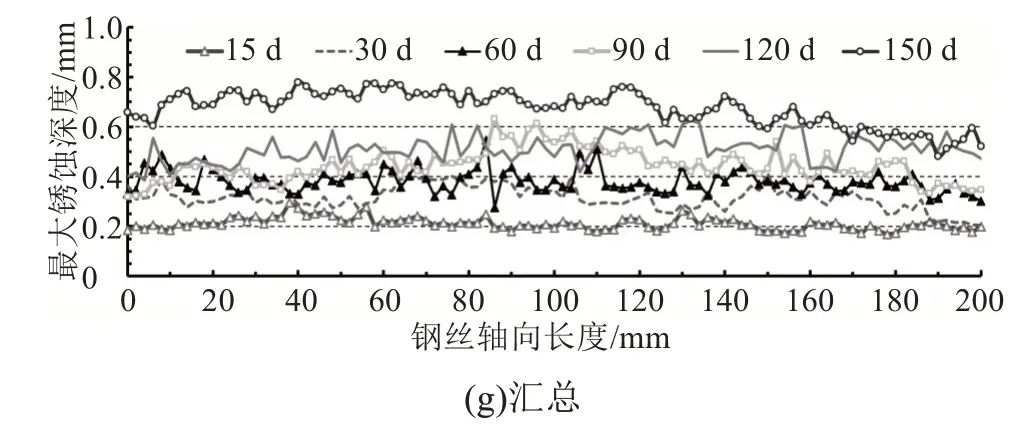
图5 不同盐雾暴露时间下最大锈蚀深度沿钢丝轴向分布Fig.5 Distribution of the maximum corrosion depth along the axis of steel wire under different salt spray exposure time

2.2 点蚀系数

许多学者在研究钢丝局部锈蚀规律时，仅研究较为严重的腐蚀区域，而忽视了其他蚀坑的情况。钢丝局部锈蚀的考察参数不应局限于最大点蚀深度和宽度，还应考虑钢丝整体锈蚀的影响。因此，本研究引入点蚀系数α和β，表征钢丝局部腐蚀程度。通过本试验三维激光扫描得到数据，对18根锈蚀钢丝共约1 800个钢丝截面进行计算分析，研究了钢丝整体锈蚀情况，并考虑了钢丝整体锈蚀深度对最大点蚀深度的影响，点蚀系数计算式为：

式中：dl,max为整根钢丝最大锈蚀深度；dl,av为整根钢丝平均锈蚀深度；dm,max为钢丝断面最大锈蚀深度；dm,av为钢丝断面平均锈蚀深度。

各参数如图6 所示。点蚀系数α和β均不小于1。当α越大，则钢丝轴向各截面坑深差别越大，腐蚀程度越不均匀。同理，当β=1时，钢丝在径向发生均匀腐蚀，横截面直径变小，仍近似保持圆形；当β越大，则钢丝微段表面轮廓线越不规则。

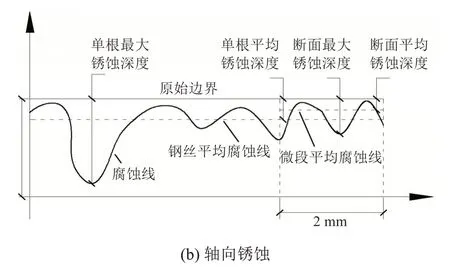
图6 锈蚀钢丝径向及轴向示意Fig.6 Schematic diagram of corroded steel wire in radial and axial direction

系数α随质量损失率变化曲线如图7 所示。从图7可以看出，随着钢丝质量损失率的增加，点蚀系数α逐渐减小，表明钢丝轴向锈蚀程度随锈蚀水平增大趋向均匀。

图7 点蚀系数α和质量损失率的关系Fig.7 Relationship between pitting coefficient α and corrosion rate

不同盐雾暴露时间下钢丝试件β的频率直方图如图8 所示。从图8 可以看出，盐雾环境下暴露60 d 和120 d 的钢丝的点蚀系数服从正态分布，其余钢丝的均服从对数正态分布。随着钢丝锈蚀程度的加大，β的期望值逐渐变小。表明：钢丝径向的腐蚀程度也趋于均匀。

图8 参数β的频率直方图和拟合曲线Fig.8 Frequency histogram and fitting curve of parameter β

不同暴露时间下各钢丝β值沿钢丝轴向变化曲线如图9 所示。从图9 可以看出，在暴露时间较短时（15～30 d），β曲线相对平滑，随着暴露时间的增长（60～90 d），曲线波动范围逐渐变大，待暴露时间到达120 d 时，曲线再次趋向平缓。表明：钢丝锈蚀初期，钢丝各微段的均匀锈蚀情况沿长度方向差异不明显。随着锈蚀的加剧，各微段锈蚀程度差异逐渐较大，当钢丝锈蚀到达120 d时，各微段锈蚀情况又趋于平缓。

图9 不同锈蚀程度钢丝点蚀系数β沿长度方向变化趋势Fig.9 Trend of pitting coefficient β of steel wire with different corrosion degrees along the length direction

统计18 个α值和1 800 个β值，得到了其频率直方图和拟合的概率密度曲线，如图10 所示。从图10 可以看出，α值主要分布在1.5～1.7，84.7%的β值集中在1.1～1.6，经检验，α和β均服从对数正态分布。

图10 α和β的频率直方图Fig.10 Frequency histogram of coefficients α and β

3 结论

对拆除的实桥吊索钢丝进行酸性盐雾加速腐蚀试验，基于三维激光扫描技术精确呈现了高强钢丝的锈蚀规律，引入点蚀系数描述钢丝不均匀锈蚀特征。得到结论为：

1）暴露在盐雾环境中的镀锌高强钢丝，质量损失率随锈蚀时间的变化呈近似幂函数的规律变化。

2）当高强钢丝在酸性盐雾环境中暴露时长达120 d 时，其点蚀系数趋近于1，即径向和轴向最大蚀坑深度趋于平均蚀坑深度，钢丝锈蚀特征趋向于均匀锈蚀。

3）引入点蚀系数α和β来表征钢丝局部腐蚀程度，统计分析了18 个α值和1 800 个β值，结果表明：高强钢丝的点蚀系数α和β服从对数正态分布。

桥梁吊索中钢丝在自然环境下腐蚀过程复杂，本研究采用盐雾腐蚀模拟自然环境与实际仍存在一定差异，需要开展大量试验进一步验证。