具有未知扰动上界的气垫船全鲁棒滑模控制
2022-07-29付明玉董李晶
付明玉,白 丹,张 坦,董李晶
(哈尔滨工程大学自动化学院,黑龙江哈尔滨 150001)
1 引言
由于气垫船特有的“两栖性”,近几年在军事和民用等领域得到了广泛应用[1].全垫升气垫船较一般水面船特有的半密封柔性裙板气垫系统,使其在航行时与水面的接触很小,因此具有较高的航速,但对环境干扰,特别是风干扰更加敏感,受到的力较其他水面船更加复杂[2].如图1所示,由于气垫船航道的复杂多变[3],阻尼系数变化范围较大,在实际中很难精确测量,也很难根据历史经验获得,这给气垫船的轨迹跟踪控制带来了更大的挑战[4–5].其中基于各种观测器进行前馈补偿,同时结合快速收敛的滑模控制器是解决系统强不确定的一种重要的研究方法[6],并已经被很多专家学者成功的应用到一些实际问题中[7].

图1 行驶在复杂的环境中的气垫船Fig.1 Hovercraft traveling in a complex environment
随着气垫船控制系统复杂程度的增加,系统不确定问题的产生原因增多.文献[8]根据干扰进入系统的渠道不同,将系统的不确定性分为非匹配扰动和匹配扰动.对于随机进入系统并且比较复杂的非匹配扰动,目前设计有效的观测器是较为可行的方法,同时结合控制器达到提高系统鲁棒性的目的.文献[9]研究带有随机综合不确定的飞行器轨迹跟踪控制问题,设计了一种扰动观测器和非奇异终端滑模控制器结合的控制系统.文献[10]采用反步控制器和非线性扰动观测器结合的方法改善存在建模误差和非匹配扰动的高阶控制系统.针对强耦合的内部摄动和外部未知干扰带来的高速飞行器非匹配不确定控制问题,文献[11]采用一种新的扩展观测器.文献[12]针对具有非匹配扰动,未建模动态和执行器故障的系统,提出了一种完全分布式观测器,并结合反步法设计了整个自适应控制系统,同时采用神经网络拟合非线性动态.关于气垫船非匹配扰动不确定问题的研究成果目前还不是很多,也不是非常深入.文献[13]假设阻尼系数是有界的时变参数,设计了一种线性时变系统的通用参数观测器,虽然达到了控制目的,但不能精确的描述气垫船的特点.文献[14]设计了一种鲁棒运动控制器,解决模型的不确定参数和未知扰动问题,不包括侧倾运动.文献[15]中使用模型知识神经网络(model knowledge neural networks,MKNN)的方法来处理四自由度ACV的参数不确定性,没有考虑拟合误差和环境干扰等问题.现有文献考虑未知参数和外部扰动的自适应控制方法研究中,文献[16]提出的主动实时估计和补偿系统内的不确定性,用状态观测器(status observer,SO)来观察外部扰动和相关参数的主动扰动控制,进而增强鲁棒控制.文献[17]结合参数不确定性的状态观测器SO和非线性干扰观测器(non-linear disturbance observer,NDO)估计未测状态的未建模动力学以及未知干扰.文献[18]提出了一种基于双观测器的自适应鲁棒控制方法.上述的观测器都是建立在已知扰动上界的条件下,但是气垫船在实际作业环境中,由于环境的多变复杂,往往上界的信息无法通过历史经验获得.关于扰动上界未知的干扰观测器设计问题,近两年有了一些研究成果应用在船舶领域,文献[28]针对海上船舶起重机的故障信息和未知上界扰动设计了一种模糊复合观测器,采用两个自适应律来补偿模糊逼近误差.文献[29]利用径向基神经网络逼近扰动观测器参数,但是对于模糊观测和神经网络的黑箱操作,无法进行系统的理论性分析,同时神经网络会消耗大量调节参数的时间,因此本文设计的观测器不需要外界扰动的上界信息,并针对内部不确定性的特点设计了合适的自适应调节率,同时设计了观测补偿项,减少系统的观测误差.
众所周知,大多数扰动观测器建立在可测系统状态的基础上,在测量中难免会有一定的误差,因此轨迹跟踪任务下的反馈控制器的设计在整个系统控制中也至关重要.文献[19]针对带有参数不确定和环境扰动的三自由度气垫船模型设计了一种有限时间收敛的终端滑模控制器,虽然收敛效果较好,但执行器输出量具有较剧烈的抖振问题.刘金琨等在文献[20]中提出了满足全鲁棒滑模控制的设计条件,并应用于带有内外不确定因素的直流电机无刷系统,结果证明该方法具有很强的鲁棒性.文献[21]提出了一种改进的全鲁棒滑模控制面和一种新的控制律来满足滑模的到达条件,与传统方法比,可以消除到达相位,较小振荡且制动距离和制动时间较短.文献[22]设计了一种分层全鲁棒快速终端滑模控制器(hierarchical-global fast terminal sliding mode controller,H-GFTSMC)来实现桥式起重机系统的防摇控制.本文采用一种具有新颖切换函数的全鲁棒滑模变结构进行反馈控制,根据跟踪误差的初始值,设计控制器的参数,使系统状态从初始点到平衡点的整个过程具有较强的鲁棒性,同时大大减小系统的抖振.综上所述,本文的主要贡献是:
1) 采用一种综合观测器,针对气垫船内部参数不确定性和外部扰动的机理特点,分别设计观测器的自适应率,设计的观测器补偿项进一步减小观测器的观测误差.
2) 根据气垫船运动特性,合理假设系统总扰动的上界未知,通过一种不需要已知上界的自适应非线性干扰观测器(adaptive non-linear disturbance observer,ANDO)补偿系统外部扰动.采用主动预测和补偿的方法解决气垫船扰动“跳变”以及上界范围未知带来的控制困难问题.
3) 在此基础上,提出一种新颖的全鲁棒滑模控制器,利用带有双曲正切函数滑动切换函数,在保证系统误差快速收敛的同时,使其更接近原点附近,同时减小系统的抖振现象,使整个联动系统具有较强的鲁棒性和实用性.
通过仿真验证,该方法在处理气垫船强不确定性和强非线性系统的运动控制中具有较好的效果.在第2节中,主要介绍了气垫船的动力学系统和相关定理;第3节描述了综合观测器的设计和证明,同时给出了轨迹跟踪控制器的分析与证明;第4节是仿真实验和结果;最后,第5节是本文的结论以及待解决问题的展望.
2 气垫船的建模与预备知识
本节主要给出了全垫升气垫船的运动学和动力学模型,同时描述了在后面章节中可能引用到的相关引理.针对给出的机理模型提出气垫船在轨迹跟踪过程中存在的内外不确定问题.
2.1 预备知识
引理1[23]已知∀t ∈Rn{0},存在一个连续函数V(t)≥0正定,并且函数V(t)存在一阶导数(t),总是满足
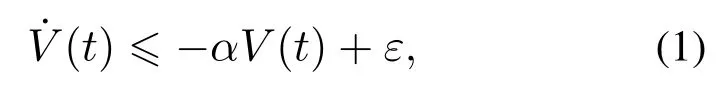
其中:α和ε表示正常数,α,ε>0,对上述不等式进行积分可得
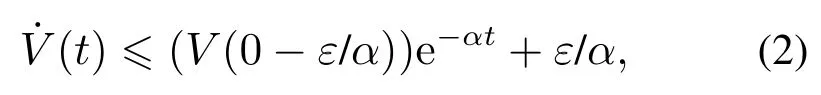
由上式可知V(t)可以指数收敛于半径为ε/α0.5的开邻域,其中V(0)是V(t)的初始值.
引理2同引理1存在函数V(t)和它的一阶导˙V(t),如果满足下面不等式:
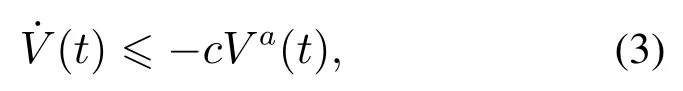
其中0
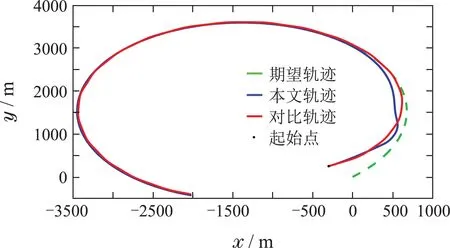
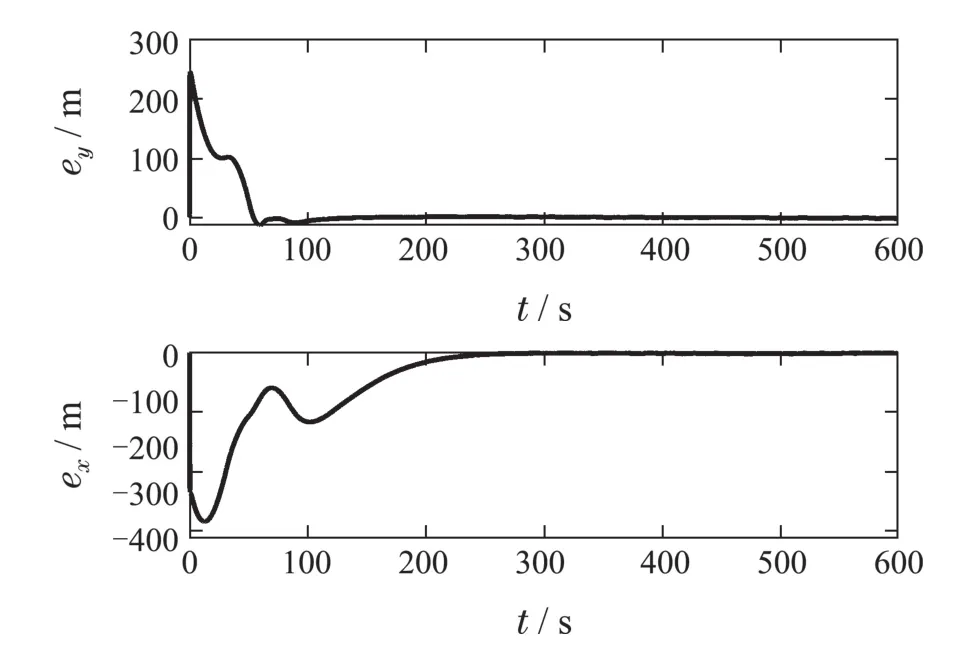
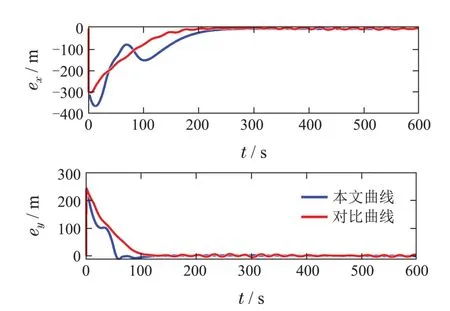
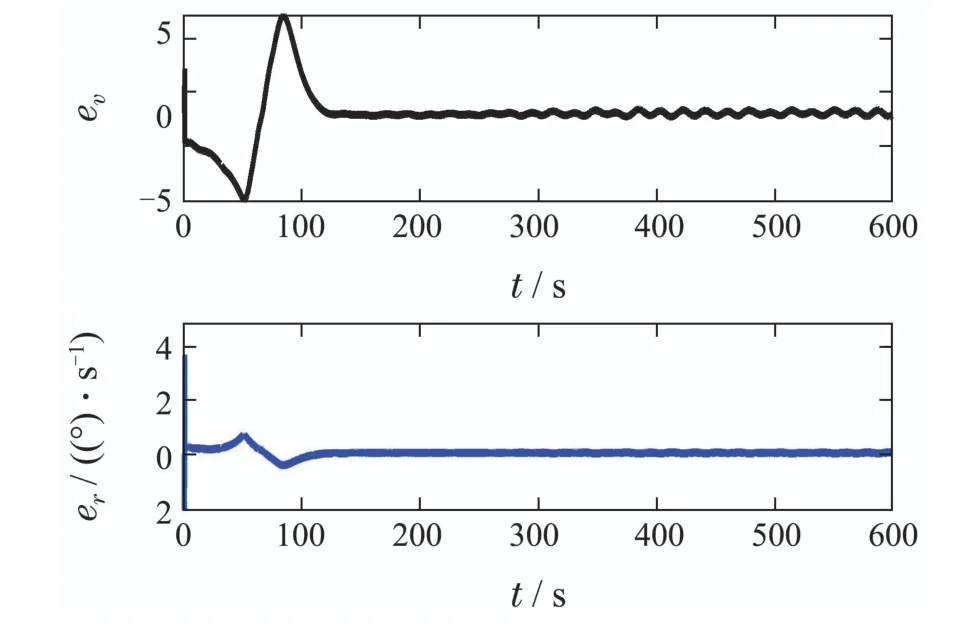
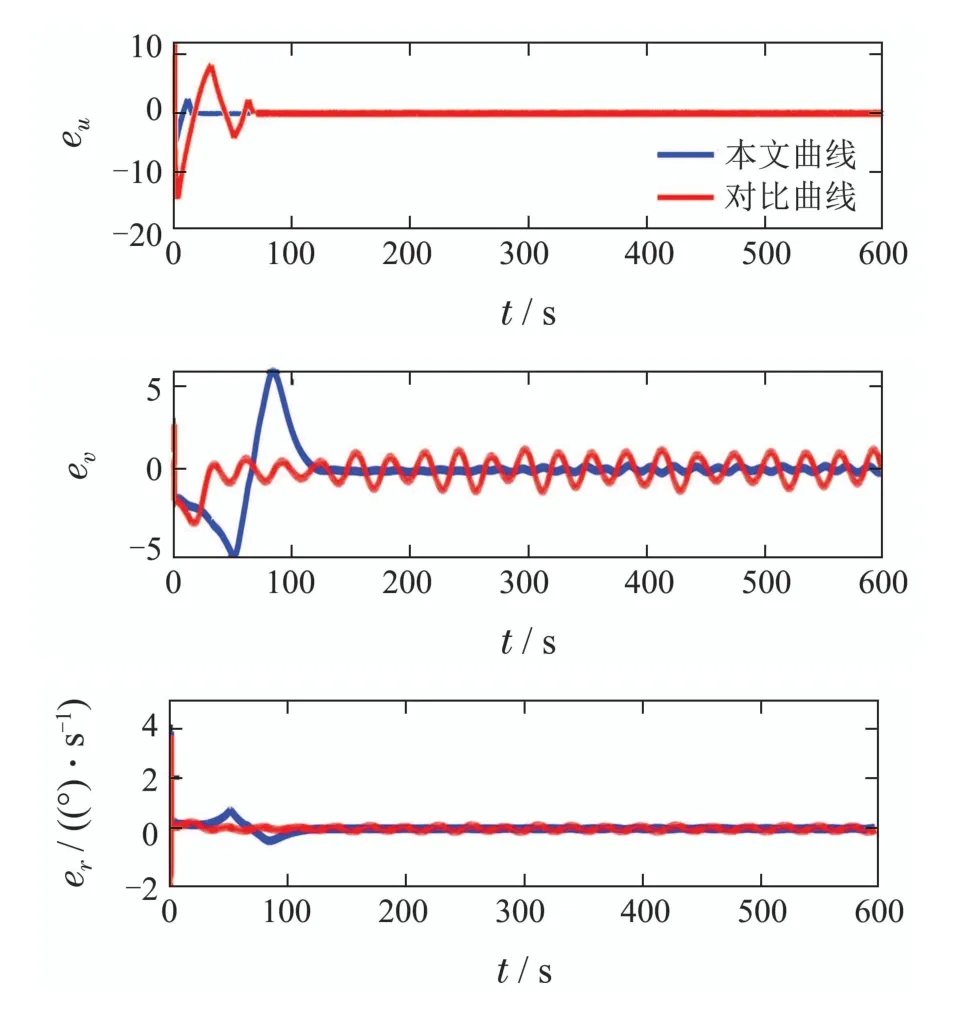
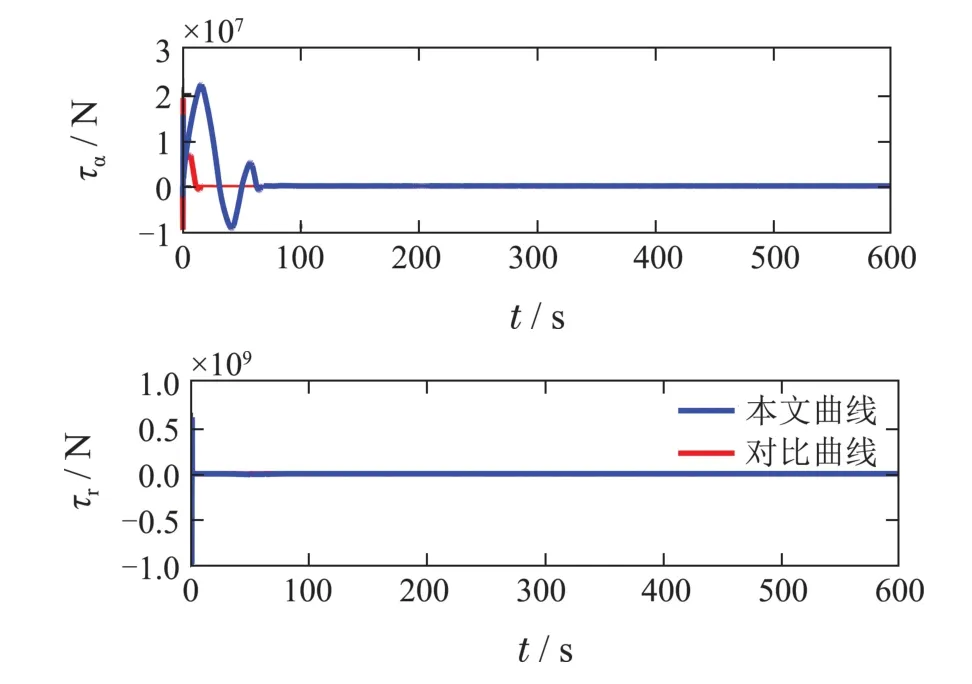
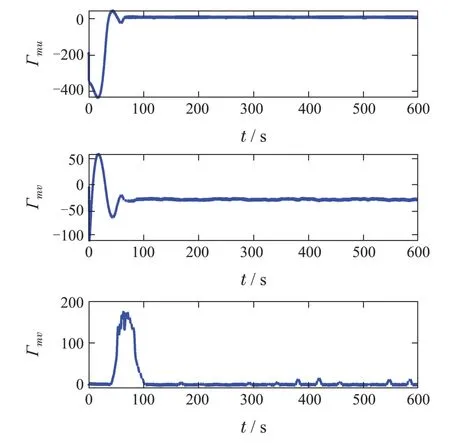
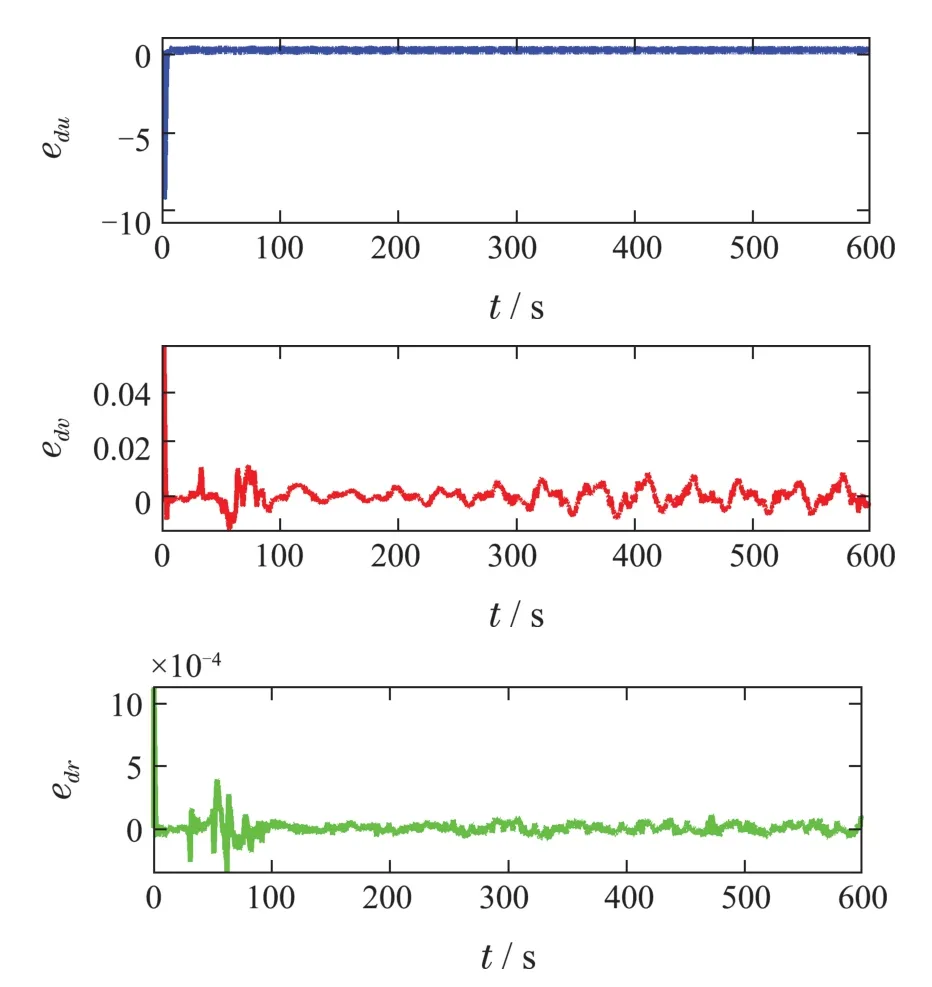
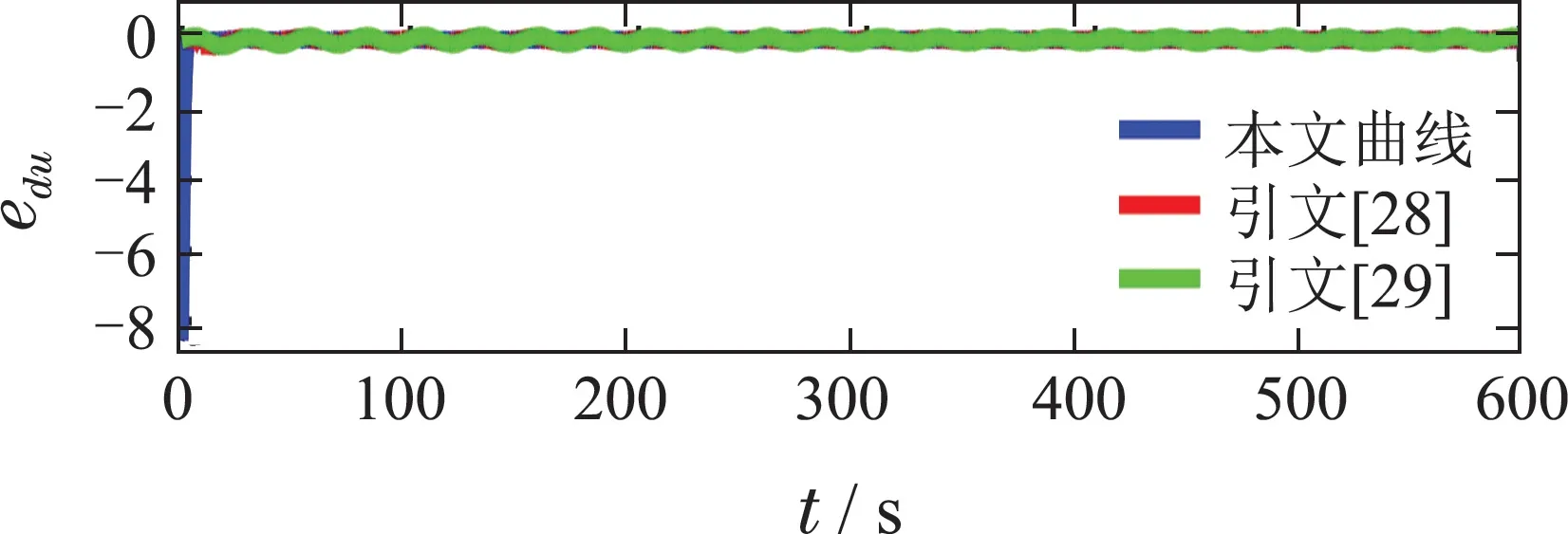
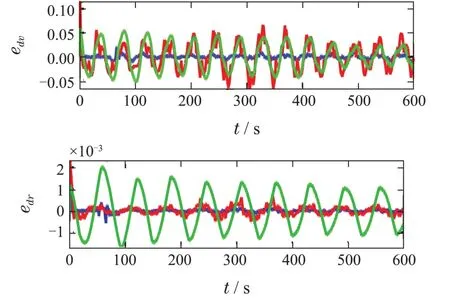
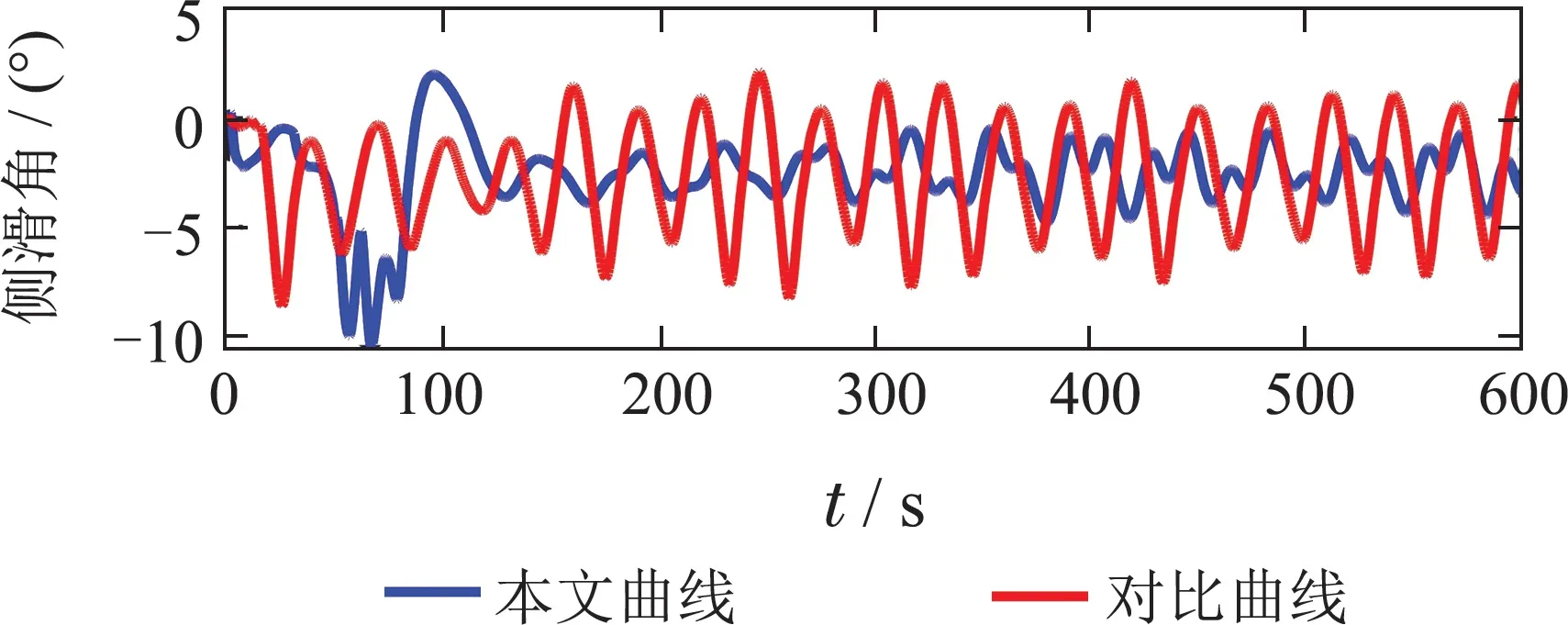
引理3假设a,b是非负实数,m>1,0 等号成立当且仅当am=bn. 在本文中,∥·∥表示Euclidean范数,|·|表示变量的绝对值,Σ(·)表示多个变量求和,[·]T表示矩阵的转置,为变量的估计值,为变量的估计误差,或是变量的控制误差. 根据Fu等人在文献[24]中所提出的气垫船4个自由度矢量模型,结合实船的基本特性,本文气垫船的运动学和动力学模型如下所示: 其中 η=[x y φ ψ]T表示气垫船在大地坐标系下的位置状态,x,y分别是沿着x和y方向的纵荡位置和横荡位置,φ和ψ分别是艏摇角和横倾角.v=[u v p r]T表示气垫船在船体坐标系下的速度状态,u和v分别为船的纵横方向的速度,p为船的横摇角速度,r为艏摇角速度. 其中:M=¯M+∆M,m,Jx,Jr分别为气垫船的质量和惯性矩,∆m,∆Jx,∆Jr是未知附加质量和惯性矩,C(v)为科里奥利力矩阵,D(v)为非线性的阻尼矩阵,是与船体坐标系中的风速矢量有关的阻尼矩阵为扰动. dij(i,j=1,2,3,4)是与系统状态相关的未知函数,k(·)为未知常数,具体描述详见文献[24],τ=[τu0 0τr]T是控制器的输出. 注1已知D(v)v和是与不确定参数和状态有关的函数,是气垫船受到的空气阻力,空气动量力,围裙阻力,泄流力以及气垫力有关的合力,详见文献[25]. 结合系统动力学模型(5)和注1,将模型简化为如下表达式: 假设1根据上述描述,本文合理假设,Γm满足如下等式: θ是未知并且可导函数,将会是与系统状态有关的函数,具体描述在下一节中给出. 考虑全垫升气垫船在高速航行状态下的轨迹跟踪控制问题,采用全鲁棒滑模变结构控制(global sliding mode control),一种全程滑动模态的滑模控制器.这种控制器使系统控制的全过程都具有鲁棒性,消除传统滑模控制中存在的趋近过程,在满足对外部扰动和内部参数摄动不敏感的同时,达到了缩短达到时间的优点.文献[20]给出了全鲁棒滑模设计通用的非线性动态滑模面,已知滑模面为f(t)应该满足的3个条件: 注2与现有研究成果[21,26–27]相比,本文设计的滑线,更容易捕捉到运动点,更适合具有很难预测阻尼系数变化范围的气垫船控制系统,同时对外部扰动具有更强的鲁棒性. 在本节中,一种改进的带有观测补偿项的综合观测器用来估计和补偿气垫船运动系统的内外不确定扰动,此观测器不需要扰动的上界信息,同时设计了一种新颖的带有双曲正切函数的全鲁棒滑模控制器,使系统能够在完成设定轨迹的同时减小抖振和跟踪误差,大大增强了整个系统的鲁棒性. 根据动力学模型(11),设计如下的综合观测器: 注3与现有的一般参数观测器[13]不同,本文气垫船动力学模型中总的力和力矩的非线性项的上界可以是未知的,θ的有界条件被释放. 假设2设定总扰动的上界为ξ,满足如下不等式: 注4本文的总扰动是未知的,并且总扰动的上界信息也是未知的,这与现有文献[30]中需要已知扰动上界的观测器相比,更符合气垫船在实际航行环境中遇到的外界不确定问题. 假设3存在两个正对称矩阵P和Q使得下面不等式成立: 根据假设3,接下来给出本文观测器的证明与分析,首先定义一个Lyapunov函数Vo, 根据不等式(32)和引理1,证明系统误差可以收敛于半径为(εo/αo)0.5的球域. 定义系统的轨迹跟踪位置误差为ex=x −xd和ey=y −yd,根据系统(5)有以下等式: 其中µu >0,µv >0,πu和πv是中间变量,会在下面的证明中给出具体描述. 根据全鲁棒滑模控制器设计应满足的3个条件以及系统状态的特点,设计如下滑模面: 设计γη使得αη >0.为了让位置误差快速收敛到原点附近,接下来设计速度滑模面: 轨迹跟踪控制器设计如下: 接下来证明控制器的稳定性,整理等式(11)和式(40)–(43),求导可得 设计Lyapunov函数, 对Vc求导得 其中 并且满足αc >0. 根据上述不等式(39)和(47),以及引理1和引理2可知,本文提出的全鲁棒滑模控制器,对于给定的任意初始条件,系统的跟踪误差总是能在有限时间内快速收敛到原点附近的某一邻域内. 本文采用一艘气垫船进行仿真实验,模型的基本参数参考文献[7],其中g=9.8 m/s2,m=4×104kg,Jr=2.5×106kgm2,Jx=1.8×106kgm2.海洋的环境干扰采用正余弦的形式来模拟,产生的力和力矩的数学描述为 其中wb ∈R4是零均值高斯白噪声向量, 一阶水动力系数系数与状态变量的关系 其中C˙v,C˙r,Ckr,Cnr为已知的变动系数,Lc=29 m,仿真步长为0.2 s. 气垫船运动学和动力学系统的初始值 设计的期望速度 观测器和控制器中的参数设定如表1所示. 表1 观测器与控制器中的参数Table 1 Parameters in the observer and controller 图2和图3描述了气垫船轨迹跟踪的具体情况,分别表示了本文控制系统和文献[21]控制方法下的轨迹跟踪时间响应曲线以及设定的期望轨迹曲线.从图中可以看到本文的控制方法可以较好的完成轨迹跟踪控制的任务. 图2 轨迹跟踪的时间响应曲线Fig.2 Time response curve of the trajectory tracking 图3 轨迹跟踪误差的时间响应曲线Fig.3 Time response curve of the trajectory tracking error 图4中可以清楚的看到相较于对比方法,本文的控制器能够将轨迹跟踪误差稳定的减小到更接近零点附近的区域内,图中被放大的部分可以清楚的看到这一点. 图4 位置误差的对比曲线Fig.4 Comparison curve of position error 图5和图6为速度跟踪误差与误差对比曲线,从图中不难看出本文方法针对具有欠驱动控制的气垫船来说,具有较好的控制效果. 图5 速度误差的时间响应曲线Fig.5 Time response curve of the speed errors 图6 位置误差的对比曲线Fig.6 Comparison curve of position error 图7为推进器控制输出的时间响应曲线,可以从图中明显的看出本文的控制器响应曲线虽然在前80 s内有波动,但后面相较对比曲线没有严重的抖振现象,能够较好的保证执行器的平稳输出. 图7 推进器控制输出的时间响应曲线Fig.7 Time response curve of the thrusters control output 图8为合力与合力矩的观测器估计误差时间响应曲线,图9为外界扰动的估计误差,从两个图中可以看出不同观测率对内外扰动观测的有效性.图10为本文干扰观测器与文献[28–29]干扰观测器对比的估计误差时间响应曲线图,不难看出本文方法的优势,而且是在扰动上界未知的条件下得到了较小的估计误差. 图8 Γm的估计误差时间响应曲线Fig.8 Estimation error time response curve of Γm 图9 外界总扰动的观测误差的时间响应曲线Fig.9 Time response curve of observation error of total external disturbance 图10 扰动估计误差的对比曲线Fig.10 Comparison curve of disturbance estimation errors 此外也在图11中看到了本文漂角的时间响应曲线变化没有对比实验的那么剧烈,这说明了整个系统处在一个相对平稳的状态. 图11 漂角的时间响应对比曲线Fig.11 Time response comparison curve of drift angle 本文研究了气垫船在存在未建模动态,内外不确定性的情况下的轨迹跟踪问题.首先在4个自由度矢量模型的基础上,提出了一种不需要扰动上界信息的综合观测器,同时提出了一种新颖的全鲁棒滑模控制器,成功减小跟踪误差的同时大大的改善了一般滑模控制器带来的抖振问题,避免了推进器的物理寿命受损.在观测器设计过程中,分别考虑内外扰动的性质差异,设计不同的观测率,同时增加一个补偿项,实验结果证明了该方法的有效性.最后利用Lyapunov函数证明了整个系统的稳定性,通过上一节的实验结果验证了本文方法的有效性.在未来的研究中,将会把执行器故障等因素考虑在系统中,设计更有效观测器和控制器,争取更好的完成容错控制下的轨迹跟踪任务.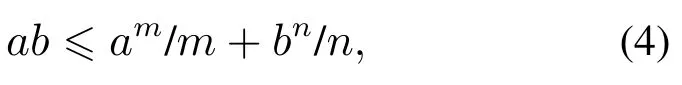
2.2 气垫船运动学模型
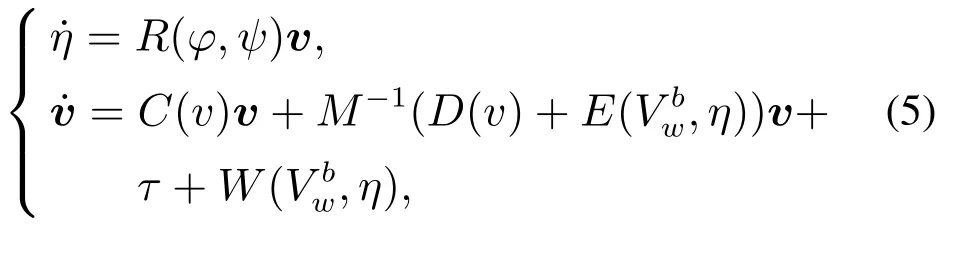
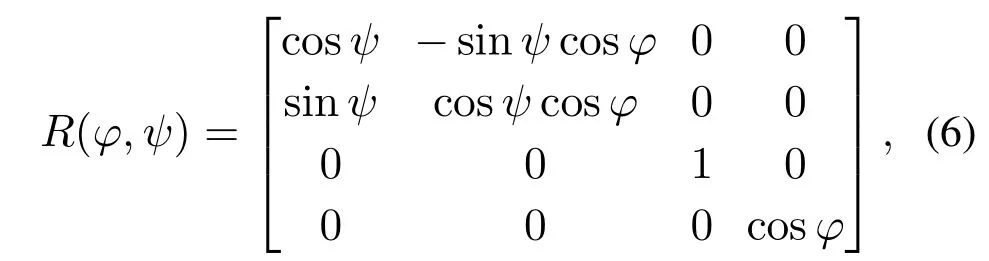
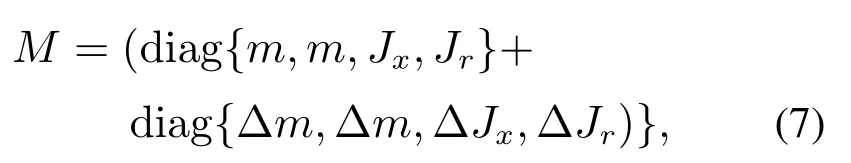

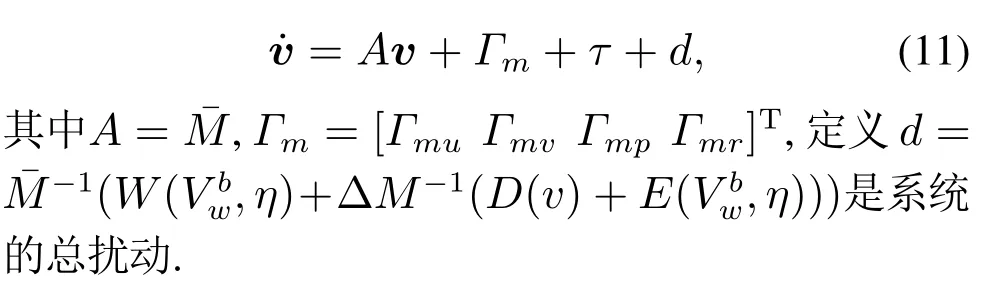

2.3 全鲁棒滑模控制器

3 观测器和控制器的设计与分析
3.1 观测器的设计与分析



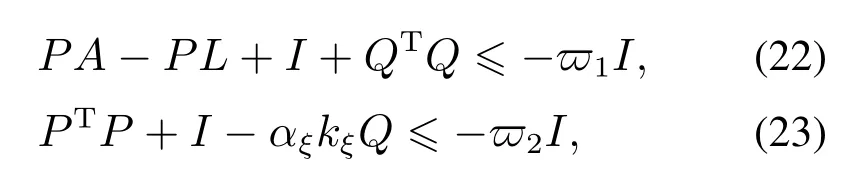
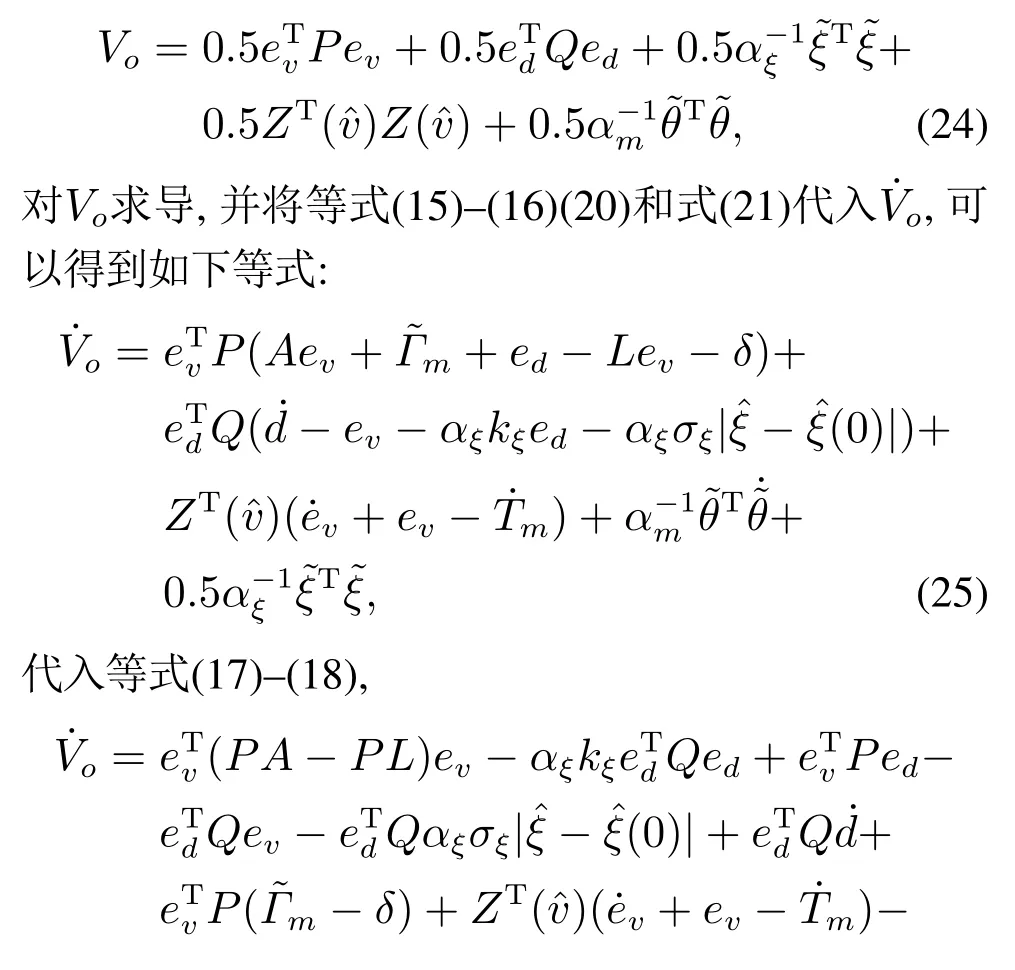

3.2 控制器的设计与分析


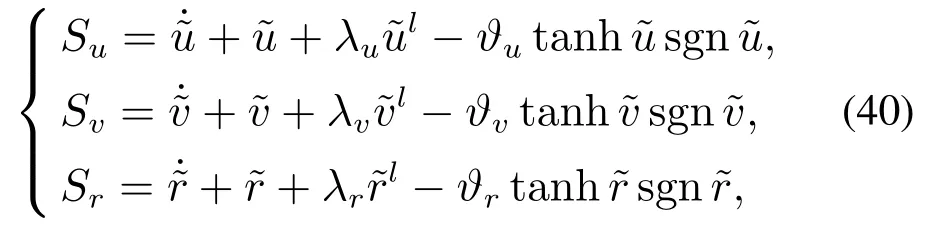
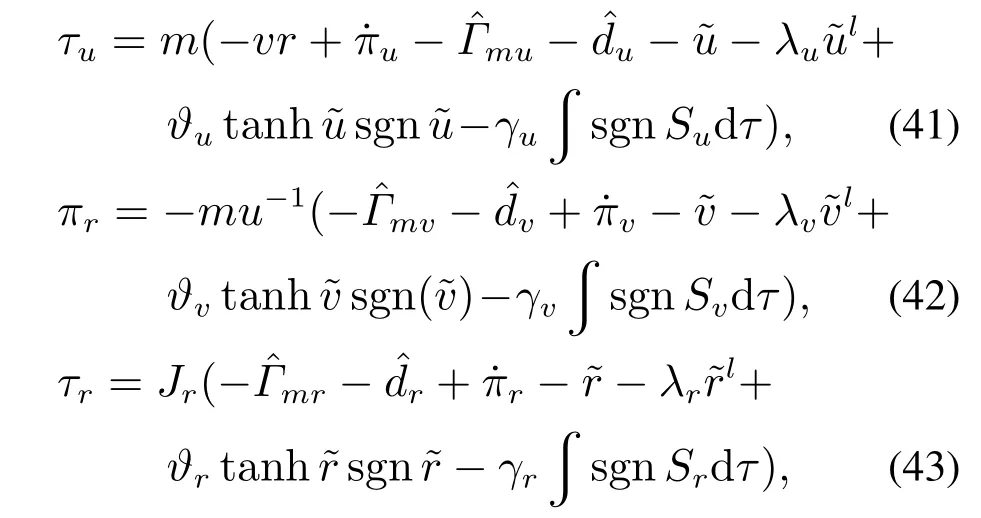
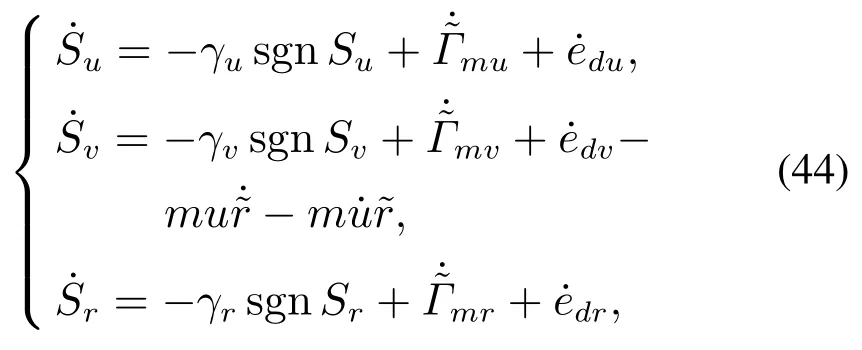
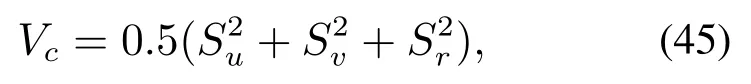
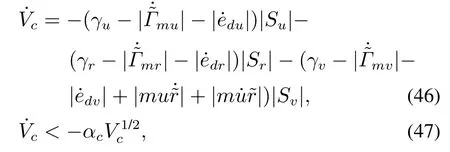
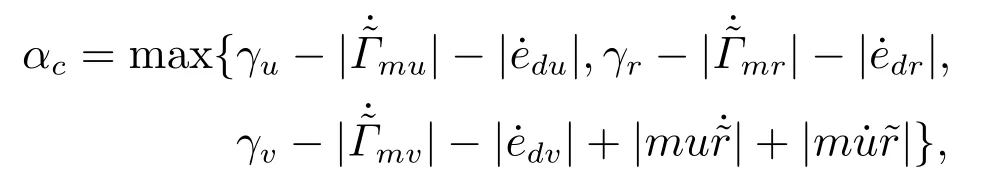
4 仿真实验
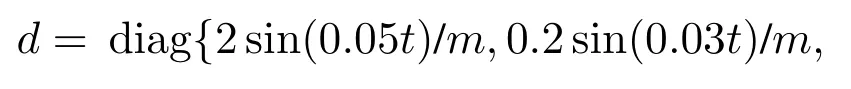
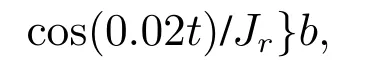
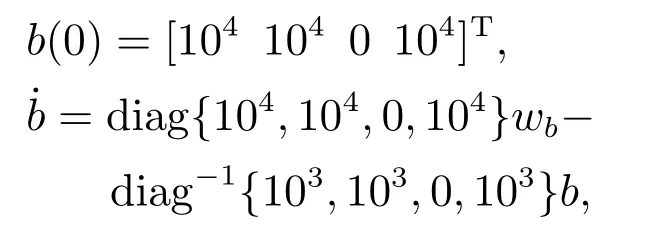
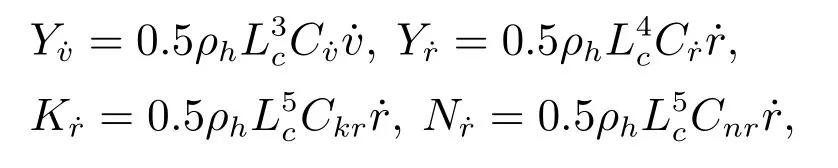
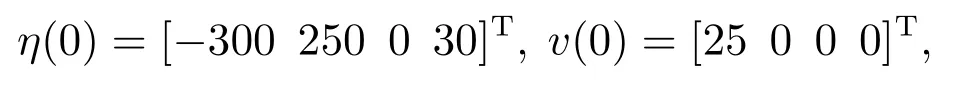
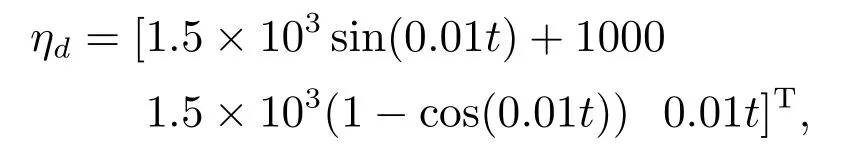


5 结论
