基于模态曲率差归一化的简支梁损伤识别
2022-07-28狄生奎李永广项长生王立宪
狄生奎, 李永广, 项长生, 王立宪
(兰州理工大学 a. 甘肃省土木工程防灾减灾重点实验室, b. 西部土木工程防灾减灾教育部工程研究中心, 兰州 730050)
改革开放后,桥梁作为跨越空间障碍物的关键结构被大量建设.近年来,由于桥梁结构材料的老化、承受过量荷载和疲劳载荷等影响,主要受力的梁结构损伤由小变大,当损伤达到某一极限时导致结构整体破坏,引发大量的安全事故[1-2].由欧进萍院士提出的结构健康监测作为“结构工程第四驱动之轮”越来越受到国内外工程师的关注和重视.
结构一旦产生损伤,将降低刚度增加阻尼,改变结构的固有模态.故利用动态测试方法获取结构的振动模态信息,进而识别损伤.损伤识别指标一般要求结构发生损伤后能定性判断损伤是否发生,对损伤位置进行定位,评估损伤大小进而对结构剩余寿命进行预测,损伤识别关系[3]如图1所示.Pandey等[4]提出了一种以模态曲率作为识别和定位损伤的方法,该方法为传统的利用模态信息识别损伤奠定了基础;狄生奎等[5]提出了基于柔度曲率差作为识别损伤的方法,该方法直接利用损伤前后的柔度曲率差,然而识别结果在高阶模态下误判性较大;战家旺等[6]提出了一种基于冲击响应的装配式板梁桥铰接缝的病害动力评估方法;张宇飞等[7]提出了基于频响函数虚部的梁结构损伤检测方法对损伤进行识别,当损伤较多时,频响函数虚部矩阵庞大,在工程实际应用中存在困难;李林等[8]提出了基于振型转角改变的框架梁损伤检测方法,该方法以敏感性分析为基础,以节点振型转交改变为损伤指标,得到的实际损伤与预测损伤基本一致,具有较好的优越性,然而由于该方法采用迭代算法,当结构自由度较多时可能导致结果不收敛;宋福春等[9]以某市绕城高速公路互通式立交桥的健康监测作为依托背景,根据现场大量的温度、位移和应变的实时监测数据,利用灰色关联分析法对所获得的监测数据进行分析,表明健康监测对城市桥梁安全使用的重要意义;徐凌等[10]采用半包粘贴CFRP加固桥梁为损伤结构的继续使用提出了新方法.

图1 损伤识别层次Fig.1 Damage identification hierarchy
由于频率反应结构的整体特性不能用于损伤识别,而振型虽对损伤具有一定的敏感性,但传统的直接利用振型的损伤识别方法对识别结果仍然具有一定的模糊性,不能对损伤进行精确定位.基于上述原因,本文以一简支钢梁为研究对象,以损伤前后振型曲率差为基础,对曲率差进行归一化,再利用归一化的结果构建指标对损伤识别进行研究.由于结构的模态信息易于测得,且指标识别结果准确,因此在工程上具有很高的利用价值.
1 损伤判别因子理论基础
由材料力学可知,梁中性面的曲率方程为
(1)
式中:K(x,t)为梁上任意点任意时刻的曲率;ρ(x,t)为梁上任意点任意时刻的曲率半径;M(x,t)为梁上任意截面任意时刻的弯矩;EI(x)为梁上任意截面的抗弯刚度.
1) 损伤的两种假定:
① 材料的弹性模量降低,而质量和截面形状不发生变化;
② 结构的截面面积减小而其余不变.
2) 本文的三个假设:
① 梁结构的质量和截面形状在损伤前后均不发生改变,仅由于弹性模量的降低造成损伤.
② 损伤程度为d,其表达式为
(2)
式中:E为梁结构无损伤时的弹性模量;E′为梁结构损伤后的弹性模量.本文仿真算例d=5%、15%、25%.
③ 假定梁结构在发生损伤后仍处于线弹性阶段,即材料不发生非线性.
基于以上假定,假如结构发生损伤,则其弹性模量由E降低为dE,由式(1)可知,梁上曲率K(x,t)增大,即x点处的曲率发生突变.图2为梁上x1、x2、x3处发生损伤后的曲率图[11].由图2可以看出,梁在发生损伤后损伤处曲率发生突变,即可以根据曲率的变化来识别损伤.假定某一梁在x点处发生了损伤d(x),可得损伤后弹性模量E′,其表达式为
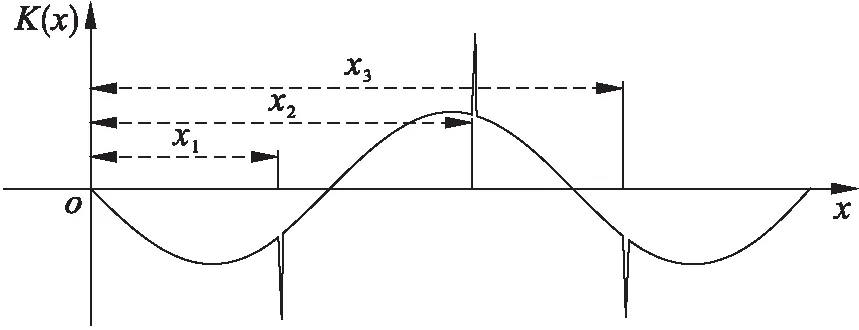
图2 梁损伤后模态曲率图Fig.2 Modal curvature after beam damage
E′=d(x)E
(3)
(4)
令δ(ω)为损伤前后对应点处的模态曲率差,则有
δ(ω)=|K(x,t)-K′(x,t)|=
(5)
由式(5)可知,δ(ω)与d(x)成比例关系.故通过δ(ω)可以识别出损伤.在某一损伤工况下,d(x)为确定值,取δ(ω)中的最小值δ(ω)min、最大值δ(ω)max,即
δ(ω)min=|K(x,t)-K′(x,t)|=
(6)
δ(ω)max=|K(x,t)-K′(x,t)|=
(7)
利用δ(ω)的最小值δ(ω)min、最大值δ(ω)max对δ(ω)进行归一化,得到DFj,即
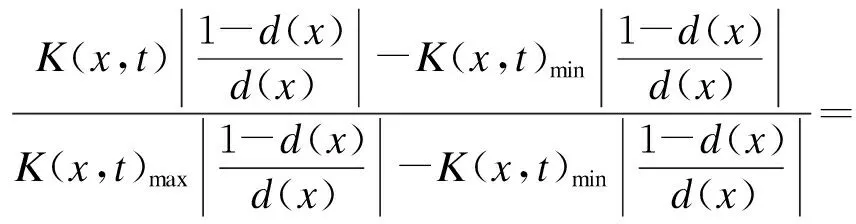
(8)
式(8)为对各点模态曲率差归一化的结果,由式(8)可知,DFj实际是对刚度的归一化,而结构的损伤导致刚度发生变化,故而DFj能对结构的损伤进行识别.由图2可知,利用模态曲率可以识别损伤,因而DFj可以用于损伤定位.归一化提高了计算精度,使模态曲率在(0,1)内变化,因此避免了利用原始数据识别时,突出原始数据中较高指标在分析中的影响和削弱数值较小指标的作用这一问题,归一化后保证了结果的可靠性,对识别结果更准确.
2 损伤判别因子DDF
由中心差分公式可得i点处振型曲率为
(9)
式中:φj(i-1)和φj(i+1)为与φj(i)相邻的i点第j阶模态的振型;li为相邻两点的距离.若结构无损伤,则振型曲率曲线连续且可导,可近似表示为一光滑的曲线,即
S(ω)=a0+a1x+a2x2+a3x3
(10)
式中:S(ω)为振型曲率曲线拟合函数;ai为拟合函数系数;x为曲线上任意一点.
若结构产生损伤,则损伤节点处刚度降低,图像将不再光滑而产生突变.由无损曲线上各点的振型曲率值与实际损伤后相应点的曲率值做差将得到损伤突变值,即
δ(ω)=|S(ω)-G(ω)|
(11)
式中:δ(ω)为曲线上各点损伤前后模态曲率差;S(ω)与G(ω)分别为损伤前后的模态曲率.
对δ(ω)进行归一化得到第j阶模态下测点i的损伤判别因子,即
(12)
Pandey等[12]提出将振型针对质量矩阵归一化后,可得到利用频率和振型表示的模态柔度矩阵,即
(13)
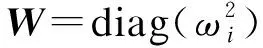
(14)

由式(10)~(14)可以看出,相对于文献[5-6],本文所采用指标在基于振型曲率的基础上推导,最终融合了前j阶模态信息,可以突出损伤处的模态信息.
3 损伤识别数值算例
3.1 数值模型
模型为一简支钢梁,长60 cm,截面尺寸b×h=8 cm×0.4 cm,钢材采取GB-50917-13(S) Q235型号钢,钢材弹性模量E=2.06×1011N/m2,泊松比μ=0.3,线膨胀系数α=1.20×10-5℃-1,容重C=7.85×104N/m3,使用质量密度ρ=8 005 N·m-3·g-1.该数值模型模拟理论简支梁受力,共21个节点,20个单元,边界条件及示意图如图3所示.

图3 简支梁有限元模型Fig.3 Finite element model for simply supported beam
3.2 损伤工况
考虑简支梁在实际工程中发生多种损伤,数值模拟7种工况,各工况的损伤通过降低弹性模量来实现,损伤程度共分为3个等级:5%、15%、25%,损伤情况分为单点损伤(5#单元)及多点损伤(5#和15#单元),各工况如表1所示.

表1 简支梁损伤工况Tab.1 Damage conditions of simply supported beam
3.3 损伤对固有频率的影响
基于上述各损伤工况,结构固有频率损伤前后变化情况如表2所示.由表2可知,各个工况同阶频率随着损伤的增大,结构的固有频率逐渐减小,与实际结果相仿.但变化的幅度不能准确对损伤进行定量及定位.
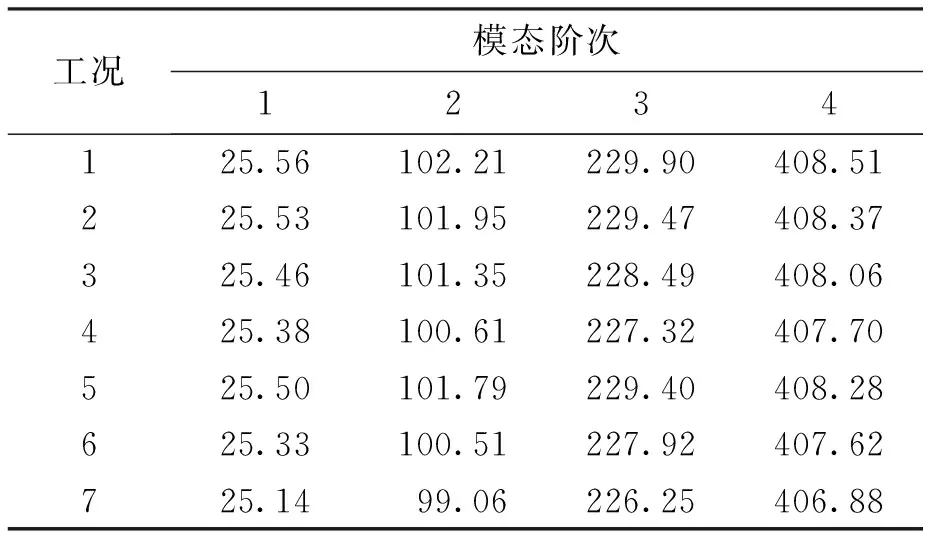
表2 损伤前后模态频率变化Tab.2 Change of modal frequency before and after damage Hz
4 分析与讨论
4.1 单个损伤情况
在工况2~4只有简支梁5#单元存在损伤,利用式(9)~(12),得到对应工况下前四阶损伤指标值DFj,由式(14)得到各工况下损伤判别因子DDF.
图4~7分别为工况2(d=5%)下,各测点前四阶DFj值.图8为工况2下各测点损伤判别因子值DDF.由于DFj与DDF为曲率指标,所以对两个边界点不能进行计算,但对于边单元依然具有识别效果.
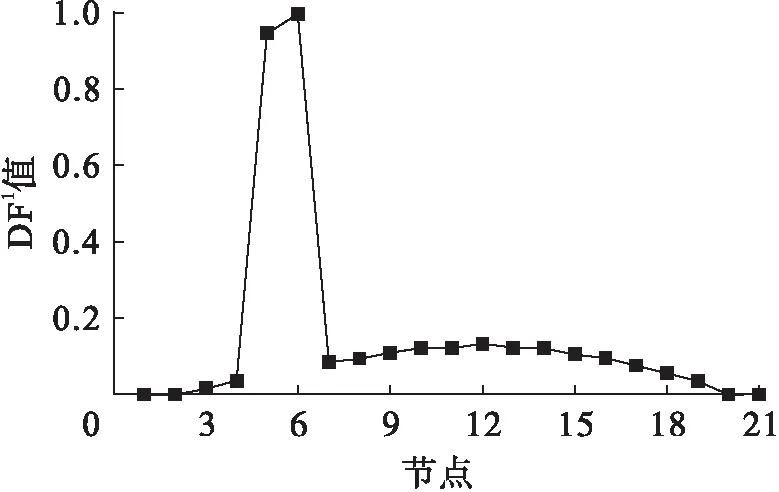
图4 工况2下各测点第一阶DF1值Fig.4 First order DF1 values at various measuring points under second damage case
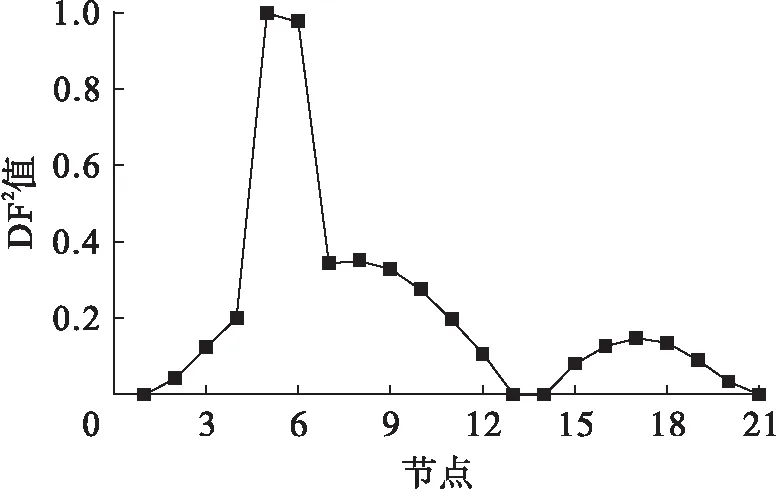
图5 工况2下各测点第二阶DF2值Fig.5 Second order DF2 values at various measuring points under second damage case
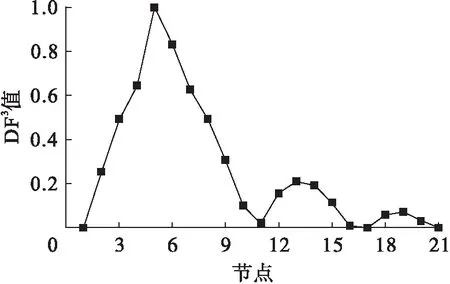
图6 工况2下各测点第三阶DF3值Fig.6 Third order DF3 values at various measuring points under second damage case
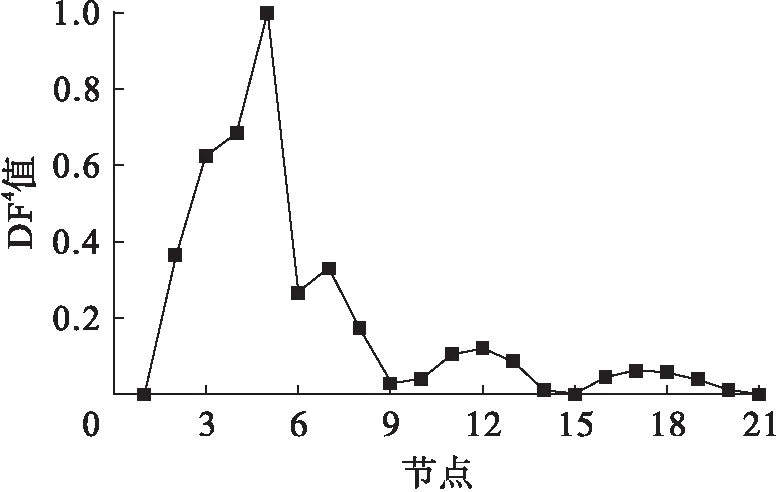
图7 工况2下各测点第四阶DF4值Fig.7 Fourth order DF4 values at various measuring points under second damage case
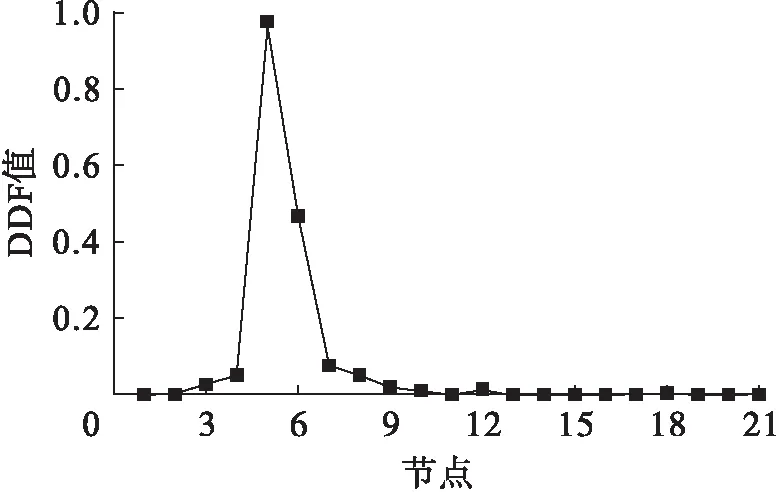
图8 工况2下各测点DDF值Fig.8 DDF values at various measuring points under second damage case
由图4可以看出,在损伤5%的情况下,DFj图形发生了尖峰突变,由DFj最大值对应的节点(节点5、6)容易识别出损伤单元.然而随着模态阶数的逐渐递增,DFj图形除在损伤单元处凸起外,在其余无损单元亦出现了凸起,即在高阶模态下对识别结果不是很理想.
由图8可以看出,融合后的指标识别效果更加准确.在一定程度上能消除在高阶模态下DFj值存在的“误判”,同时弥补在低阶模态下损伤处DFj值“不突出”的缺陷.识别结果以损伤判别因子DDF最大值对应的节点方式给出.
对比图4~7、8,指标DDF更能准确地定位损伤.图9~10为经过DFj值融合后工况3和工况4的DDF值图形.由图8~10可以看出,根据DDF最大值对应的节点能识别出损伤,因而,在任意损伤情况下,均能由DDF值进行损伤定位,且识别结果是准确的.
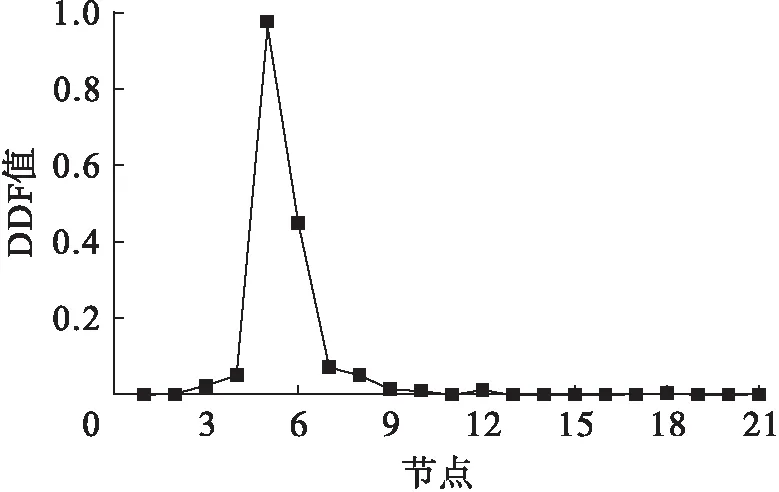
图9 工况3下各测点DDF值Fig.9 DDF values at various measuring points under third damage case
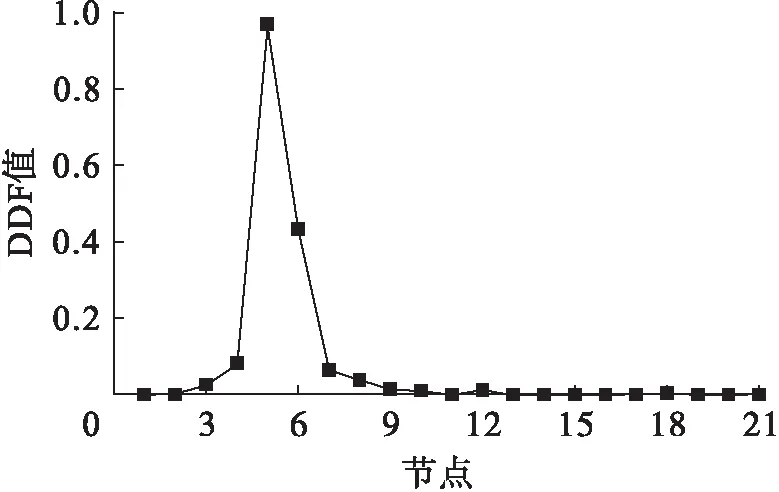
图10 工况4下各测点DDF值Fig.10 DDF values at various measuring points under fourth damage case
4.2 多个损伤情况
在工况5~7下简支梁5#单元和15#单元同时存在损伤.与单个损伤类似,依次求得DFj及DDF值并绘制成图.图11~14分别为工况6(d=15%)下,各测点前四阶DFj值.图15为工况6下各测点损伤判别因子值DDF.
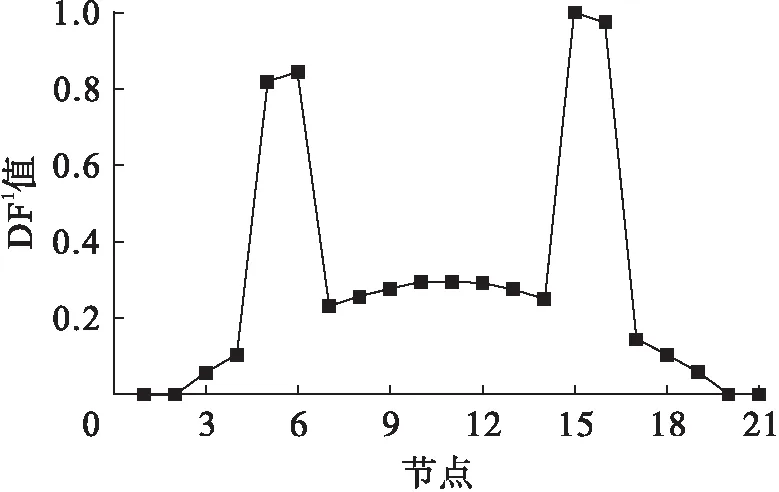
图11 工况6下各测点第一阶DF1值Fig.11 First order DF1 values at various measuring points under sixth damage case
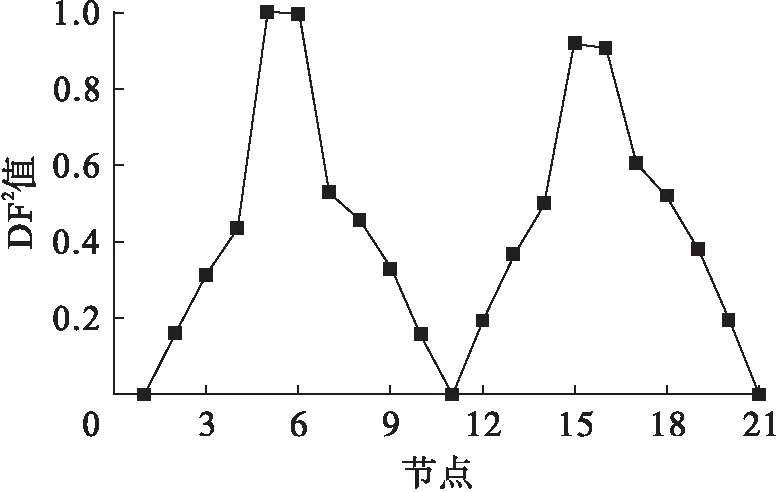
图12 工况6下各测点第二阶DF2值Fig.12 Second order DF2 values at various measuring points under sixth damage case
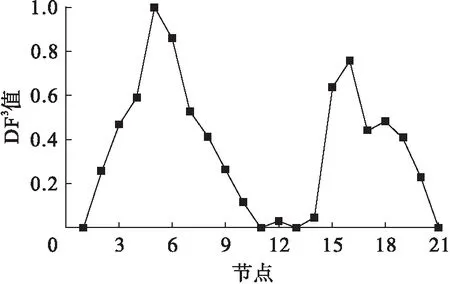
图13 工况6下各测点第三阶DF3值Fig.13 Third order DF3 values at various measuring points under sixth damage case
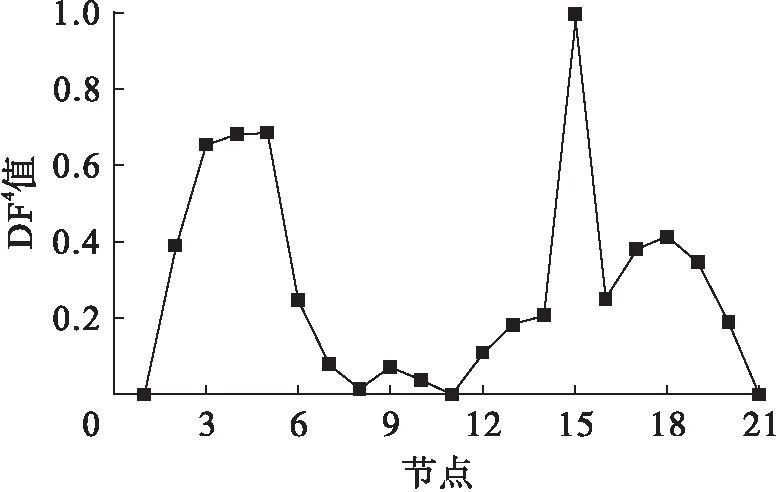
图14 工况6下各测点第四阶DF4值Fig.14 Fourth order DF4 values at various measuring points under sixth damage case
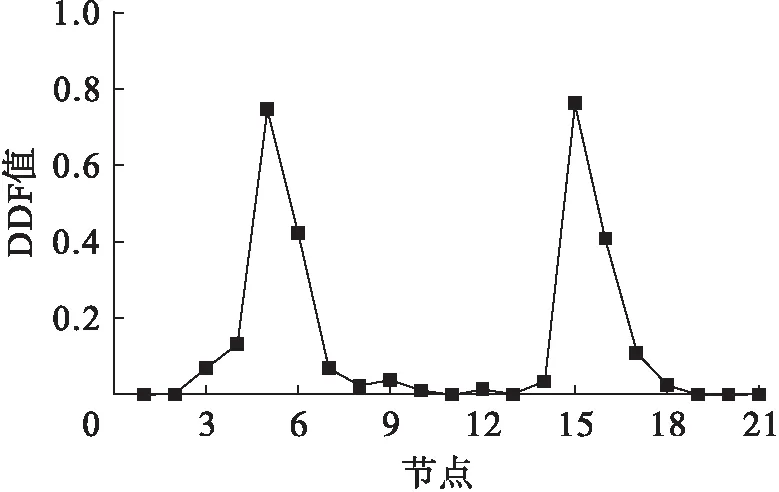
图15 工况6下各测点DDF值Fig.15 DDF values at various measuring points under sixth damage case
由图11~14可见,与单一损伤结果一致,根据DFj图最大值所对应的节点能识别出损伤单元5#及15#.然而,由于模态阶次逐渐增高,无损单元处局部凸起,对识别造成了一定的干扰.
由图15可知,利用DDF最大值对应的节点能准确识别出损伤单元.相对于DFj,DDF在一定程度上消除了低阶模态和高阶模态时的不足,识别位置是准确的.对比图11~14、15,对损伤位置的识别而言,DDF比DFj更具有鲁棒性.
图16~17给出了工况5和工况7的DDF值图形.结合图15~17可以看出,利用DDF值在任意工况下,对损伤单元均可以进行定位.
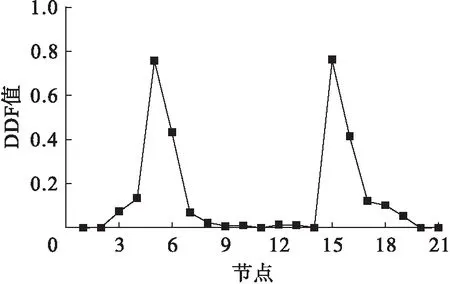
图16 工况5下各测点DDF值Fig.16 DDF values at various measuring points under fifth damage case
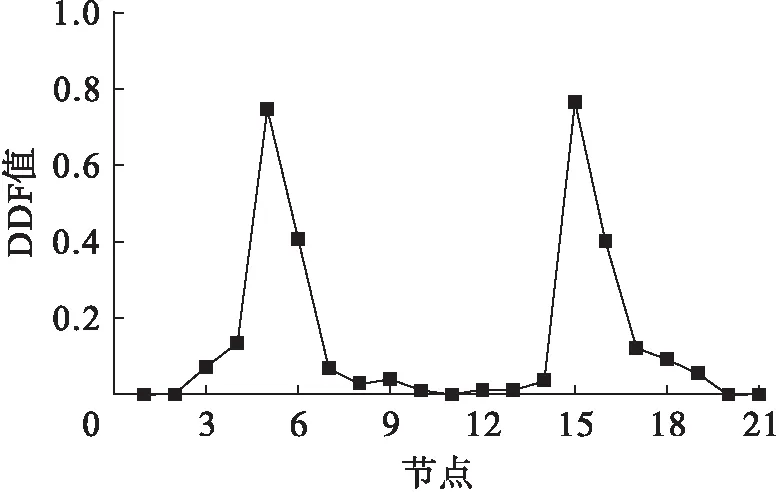
图17 工况7下各测点DDF值Fig.17 DDF values at various measuring points under seventh damage case
5 损伤曲线
δ(ω)反映了无损曲线上各点的振型曲率值与实际损伤后相应点曲率值的差,取各阶模态下δ(ω)的最大值,如表3所示.通过MATLAB利用polyfit(x,y,n)函数将表3各工况下δ(ω)最大值进行数据拟合,各式均由无损伤至损伤25%时δ(ω)最大值进行拟合.

表3 各工况下δ(ω)最大值Ⅰ
5#单元损伤5%、15%、25%的损伤评估函数见式(15)~(18);5#及15#单元损伤5%、15%、25%的损伤评估函数见式(19)~(22).构造损伤曲线如图18~19所示.
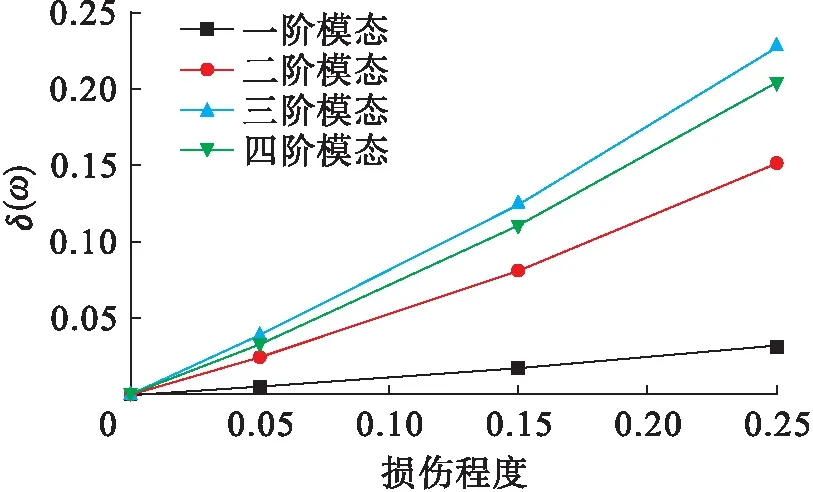
图18 单点损伤评估曲线Fig.18 Single point damage evaluation curves
F1(x)=0.146 7x3+0.084x2+0.097 4x
(15)
F2(x)=0.593 3x3+0.368x2+0.474 1x
(16)
F3(x)=0.593 3x3+0.568x2+0.730 1x
(17)
F4(x)=0.646 7x3+0.544x2+0.639 2x
(18)
F5(x)=-0.86x3+0.472x2+0.060 5x
(19)
F6(x)=-3.346 7x3+1.816x2+0.259 6x
(20)
F7(x)=-6.593 3x3+3.151 2x2+0.494 9x
(21)
F8(x)=-6.873 3x3+3.848x2+0.528 8x
(22)
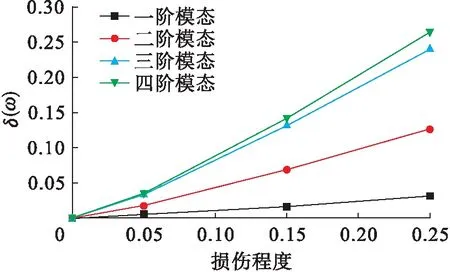
图19 多点损伤评估曲线Fig.19 Multiple point damage evaluation curves
结构振动的模态参数与物理参数息息相关,因此,结构物理参数的变化一定会导致结构振动模态参数的变化.由图18~19可知,随着损伤程度的增大,损伤前后模态差值δ(ω)逐渐增大,说明与实际结果相仿.式(15)~(22)与图18、19均是由损伤前后的曲率差值δ(ω)得到,而基于模态信息进行损伤检测的各种指标都是以此差值为基础进行构造,该差值包含了损伤最原始的模态信息,且实际操作中最易获得,故而以此进行损伤定量的推断具有一定的准确性.
损伤曲线代表了结构随着损伤程度的增加,结构损伤状况的发展趋势.随着使用年限的增加,损伤逐渐积累,因此损伤程度与结构的服役期限紧密相关.在工程实际中,可以通过不同使用期限的曲率差峰值绘制损伤曲线,即可通过损伤函数曲线对不能实际得到的损伤程度进行描述.
6 寿命预测
桥梁损伤识别的最终落脚点是对桥梁剩余寿命进行评估.桥梁结构使用寿命是服役桥梁耐久性的衡量指标,可以分为物理寿命、功能寿命和经济寿命.桥梁结构使用寿命预测方法有经验法、类比法、快速试验法、数学模型法和概率分析法等.
桥梁在服役过程中受环境、人为等因素的作用,损伤由微观裂缝发展至结构整体刚度下降,模态信息包含了不同时期损伤的发展与演化.损伤程度与结构使用周期密不可分,因此利用类比法对损伤程度进行评估,继而预测剩余寿命具有可行性.
假设结构全寿命为TF,为了使结果具有一般性,此处TF取理想状态下结构设计使用年限,剩余寿命为TR,服役周期为TE,使用期限达到全寿命时对应损伤程度为e=100%,服役期对应损伤程度表达式为
(23)
TR=TF-TE=TF-eTF=(1-e)TF
(24)
由于损伤发生在结构的使用期内,因此利用损伤评估曲线F(x)推导损伤程度e.取任意模态阶次下δ(ω)的最大值绘制损伤评估曲线,保持线形不变而重置横、纵坐标,即x轴对应构件服役周期与全寿命之比,y轴对应δ(ω)最大值.利用不同服役周期模态曲率差的最大值,通过多项式拟合构造损伤评估曲线,进而得到构件的全寿命预测曲线,如图20所示.结果表明,由于构件的差异性和损伤的不同,虽然损伤评估函数的系数待定,但通过δ(ω)的最大值绘制图像进行预测结构的剩余寿命仍具有一定指导意义.
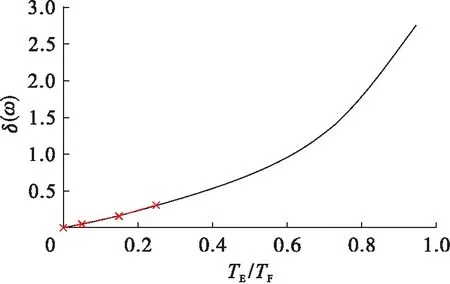
图20 全寿命预测曲线ⅠFig.20 Life prediction curveⅠ
7 试验验证与结果
7.1 损伤识别
试验以一简易等截面简支钢梁为研究对象模拟损伤识别,验证所提指标的准确性.模型横截面尺寸为100 mm×8 mm,模型净跨径175 cm,划分为35个单元、36个节点.试验钢梁材料特性为:弹性模量E=2.079 5×108kN/m2,容重C=76.98 kN/m3,泊松比μ=0.3.在单元节点处安装加速度传感器以获取结构的模态数据,测试系统如图21所示,切口细节照片如图22所示,图23为简支梁单元划分与截面尺寸(单位:cm).

图21 测试系统照片Fig.21 Photo of testing system

图22 切口细节照片Fig.22 Photo of gap details

图23 简支梁单元划分与截面尺寸Fig.23 Element division and section size of simply supported beam
对简支梁进行单点力锤激励多点加速度采集试验(SIMO),试验设备采用NV9812型压阻式加速度传感器,采用Coinv-DASPMAS模态与动力学分析软件分析测试信号,采样频率为204.8 Hz.现场采用6个加速度传感器,采用“跑传感器”的方法获取梁结构模态数据,即5个传感器为一测量组,剩余1个为参考点,以参考点测试数据为基准计算得到其他传感器测试数据的相对值,将各数据组合得到梁的整体响应数据.
为使试验更贴近实际桥梁损伤,试验共设置4个工况,分别为无损工况及3个损伤工况(在钢梁不同位置设置不同孔深的切口模拟),损伤程度为15%、30%、45%,损伤情况分为单点损伤(18#单元)、两点损伤(10#和25#单元)及多点损伤(9#、18#及26#单元),各工况如表4所示.

表4 试验梁损伤工况Tab.4 Damage cases of testing beam
试验通过力锤激励获取结构的前三阶振型进行分析,工况9仅考虑18#单元损伤15%,利用式(9)~(12),得到对应工况下前三阶损伤指标值DFj,由式(14)得到各工况下损伤判别因子DDF.
图24~25分别为工况9(d=15%)下,各测点前两阶DFj值,图26为工况9下各测点损伤判别因子DDF值.由图24~26可以看出,在损伤15%的情况下,根据DFj图中尖峰对应的节点(节点18、19)可以识别出损伤单元,但是DFj图中干扰节点影响较大,而DDF图识别损伤位置更为准确.

图24 工况9下各测点第一阶DF1值Fig.24 First order DF1 values at various measuring points under ninth damage case

图25 工况9下各测点第二阶DF2值Fig.25 Second order DF2 values at various measuring points under ninth damage case
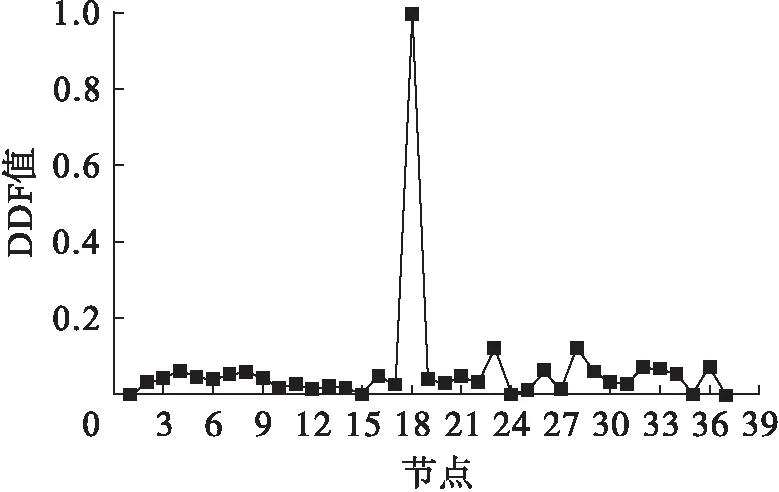
图26 工况9下各测点DDF值Fig.26 DDF values at various measuring points under ninth damage case
图27~28分别为结构两点损伤和多点损伤下DDF值.根据图中尖峰对应节点可以准确识别出损伤位置.结合数值算例及试验,易于验证所提指标工程的可行性及实用性.

图27 工况10下各测点DDF值Fig.27 DDF values at various measuring points under tenth damage case
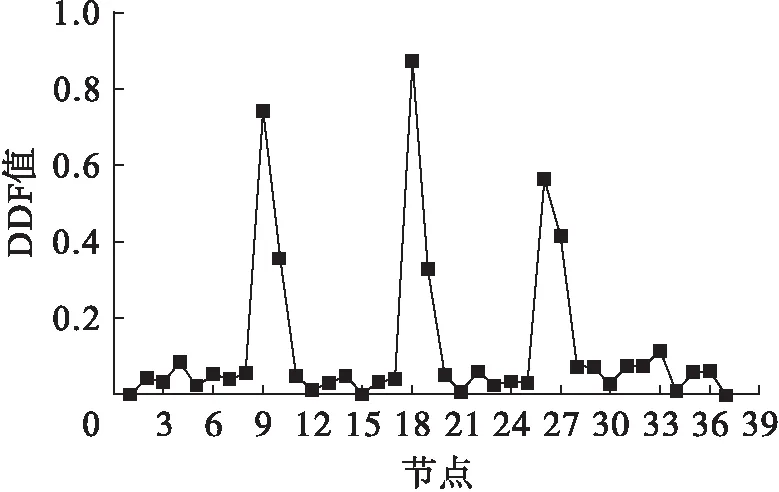
图28 工况11下各测点DDF值Fig.28 DDF values at various measuring points under eleventh damage case
7.2 损伤曲线
根据前文所述,取各阶模态下δ(ω)的最大值如表5所示.使用MATLAB中polyfit(x,y,n)函数对δ(ω)进行数据拟合得到损伤曲线函数.
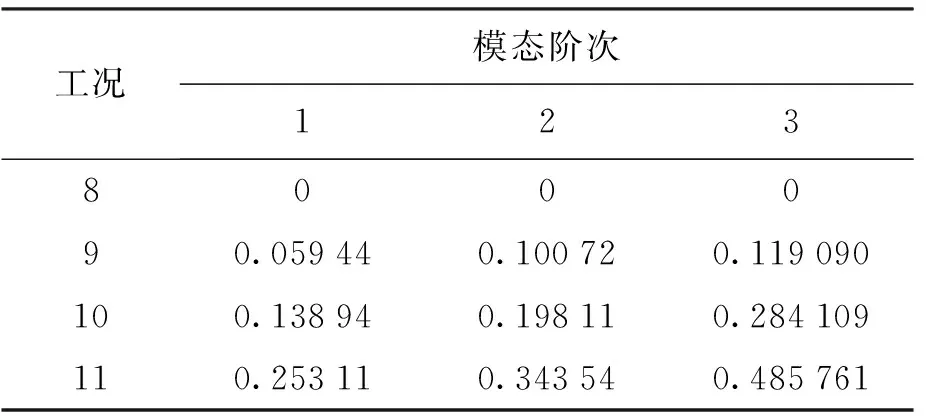
表5 各工况下δ(ω)最大值ⅡTab.5 Maximum values Ⅱ of δ(ω) under various damage cases
各工况下损伤评估曲线函数见式(25)~(27),构造损伤曲线如图29所示.
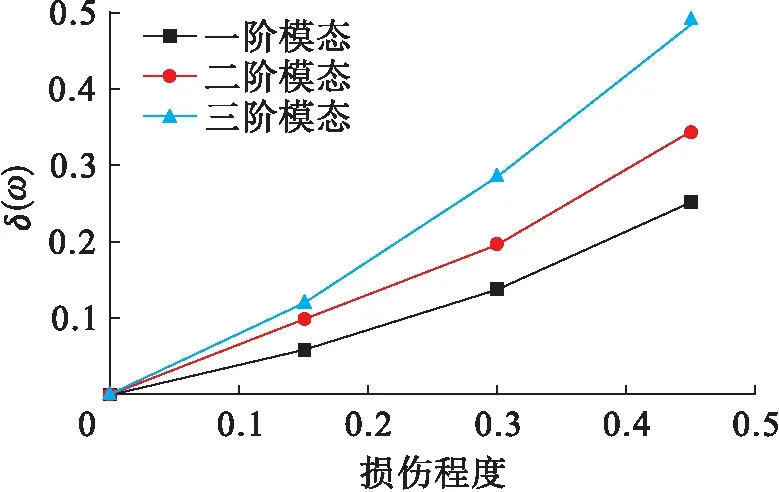
图29 试验损伤评估曲线Fig.29 Test damage evaluation curves
F9(x)=7.214 8x3+1.211 1x2+3.618 7x
(25)
F10(x)=25.367 9x3-12.155 6x2+7.967 2x
(26)
F11(x)=-4.592 6x3+12.273 3x2+6.201 7x
(27)
结构振动的模态参数与物理参数息息相关,由图29的变化趋势可知,随着损伤程度的增大,损伤前后模态差值δ(ω)逐渐增大,因此,结构的物理参数发生了变化,以此为依据进行结构损伤诊断具有一定的可行性.
7.3 结构剩余寿命预测
结构在使用期间,受到车辆荷载、温度荷载及某些不可避免的偶然荷载后,损伤逐渐形成,进而威胁到结构的安全使用.因此,对结构的剩余寿命进行评估,及时加固、维修或重建满足其使用功能具有重要意义.
试验中假设简支钢梁的全寿命TF为20年,18#单元发生损伤.利用其一阶模态δ(ω)的最大值绘制损伤评估曲线,如图30所示,并重置横、纵坐标,x轴对应构件服役周期与全寿命之比TE/TF,y轴对应δ(ω)最大值.由图30可知,当结构发生15%损伤时,δ(ω)max=0.253,TE/TF=0.45,由式(23)得x=0.45,由式(24)得结构剩余寿命TR=11年.
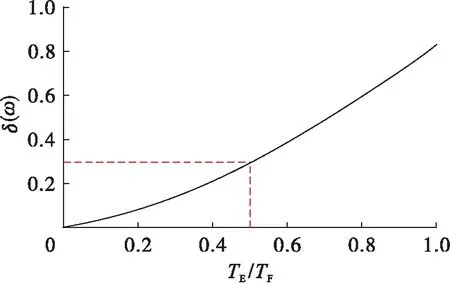
图30 全寿命预测曲线ⅡFig.30 Life prediction curveⅡ
8 结 论
本文通过分析得出以下结论:
1) 数值算例表明,无论是单个损伤还是多个损伤均能对损伤进行定位,对损伤识别具有较高的鲁棒性,且该指标能够识别小损伤(5%).
2) 简支钢梁试验表明,DDF指标可以准确识别结构的损伤位置,定性损伤程度,此指标可以克服无损节点的误判.
3) 利用损伤时任意模态下曲率差的最大值构造损伤评估曲线,利用类比法对损伤程度进行评估,继而预测剩余寿命对工程实践具有指导意义.
