基于置信度机会约束规划的风电场无功优化技术
2022-07-28胡畔冀肖彤王易张兆毅赖秋频刘承锡
胡畔, 冀肖彤, 王易, 张兆毅, 赖秋频, 刘承锡*
(1.国网湖北省电力有限公司电力科学研究院, 武汉 430077; 2.武汉大学电气与自动化学院, 武汉 430072)
随着全球经济快速发展,世界各国能源消耗量越来越大,化石能源造成的环境污染成为日益关注的问题,大力发展清洁能源已成为共识。伴随着中国“碳达峰,碳中和”目标的提出,新能源将进入快速发展时期[1],风电作为重要的清洁能源,其开发和利用对缓解环境压力和实现低碳经济具有重要意义[2-3]。
风电大量接入电力系统,其间歇性和不确定性给电力系统的安全稳定运行带来很大挑战[4]。特别是电压越限问题会威胁到系统的安全运行,引发国内外学者广泛研究[5-7]。文献[8]考虑风电预测的不确定性对多时段电压边界的影响,通过优化使得所提出的电压控制策略的多时段目标成本最小。文献[9-10]建立了多时间尺度的电压协调模型来解决高渗透率分布式电源引起的电压越限问题。文献[11]利用滚动时域优化控制方法,通过建立反馈修正框架来实现电网无功调配和应对不确定性能源带来的电压稳定问题。鲁棒优化和随机优化是含不确定能源系统优化重要的研究方法[12],通过在目标函数中引入鲁棒优化和随机优化的权重因子,来实现鲁棒优化和随机优化的协调,从而克服随机优化计算量大和鲁棒优化方法过于保守的缺点[13-14]。文献[15]提出了一种采用两阶段分布鲁棒机会模型的优化调度方法,用来解决分布式电源及负荷不确定性导致的配电网电压越限问题。文献[16]提出了一种考虑电压和功率越限双重风险的日前优化调度方法,以运行成本与越限综合风险最小化为目标,通过优化来兼顾主动配电网的调度经济性与安全性。文献[17-18]引入灵敏度系数来衡量功率变化对电压的影响,提出了基于灵敏度系数调节电压的方法。文献[19]采用罚函数的方法处理电压越界问题,通过调整罚函数系数达到控制电压越限风险的要求。
以上文献均从不同的方面和方法对含不确定能源接入系统的电压越限问题进行研究。现以网损最小为目标函数,考虑风电预测误差对系统的无功优化的影响,确定下一时刻系统的最佳运行状态。利用仿射函数将风电预测误差的概率分布映射到电压的概率分布,通过一定置信度下的电压约束来控制电压越限风险。提出根据风电预测精度来确定无功优化的约束,使其能够满足不同风速下各种运行工况的要求。采用解析化梯度矩阵和海森矩阵的改进算法来提高计算的收敛速度。通过含风电场的IEEE-39节点输电系统和中国内陆某实际风场配电系统的案例,验证所提方法的有效性和优越性,并总结输配电网进行无功优化时电压的变化规律。
1 风电接入系统的无功优化方法
1.1 风电预测模型
风电的间歇性和不确定性使风电功率预测存在误差,风电时间自相关性和空间互相关性[20-21]增加了风电预测的复杂性。为了使风电不确定性对系统电压的影响原理更加清晰,设风电预测误差服从常见的正态分布[7],其分布一般可根据当地风场历史运行数据获得。正态分布模型的好处在于,在考虑风场时空相关性后,功率预测误差经线性仿射函数映射(即线性组合)所得的电压幅值和相角偏差量仍然服从正态分布,其概率分布性质可由标准差或方差来衡量。
含风电接入的电力系统,通常短期和超短期风电预测精度高于中长期风电预测精度,但它们的适用场合不同。因此,有必要根据风电功率预测精度和应用场合来合理选择不同的优化方法,使优化结果更具工程实用性。
1.2 随机优化模型的转化
由概率论定理推论可知,m个随机量服从m元正态分布的充分必要条件是m个随机量的任意线性组合均服从一维正态分布,即由式(1)可得到式(2),表达式为
ξ~N(α,R)
(1)
sTξ~N(sTα,sTRs)
(2)
式中:ξ和α分别为m维随机向量及其期望向量;R为协方差矩阵;s为任意的m维向量。
假设风电预测误差引起的节点有功和无功不平衡功率服从均值为0的2n元正态分布,n为系统节点数,故系统不平衡功率的相关系数矩阵和协方差矩阵分别为
(3)
(4)
式中:Aρ为系统不平衡功率的相关系数矩阵;ρi,j为第i个和第j个不平衡功率间的相关系数;R为协方差矩阵;δi为第i个不平衡功率的标准差。
在某一运行点,由节点功率平衡方程的雅克比矩阵可以推导出灵敏度系数矩阵S,用来表示节点功率不平衡量对节点电压幅值和相角的影响,公式为
(5)
式(5)中:SVP、SVQ、SθP和SθQ为分块矩阵,组成灵敏度系数矩阵S;ΔP和ΔQ分别为节点有功和无功不平衡量向量;ΔV和Δθ分别为节点电压幅值和相角偏差量向量。
经过式(5)所示的线性仿射变换,得到的电压幅值和相角偏差量也服从一维正态分布,其均值为0,其方差分别为
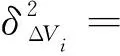
(6)

(7)

求得电压幅值和相角偏差量的正态分布后,进而可得在β置信度下的最大电压偏差量,即置信区间半宽,如式(8)和式(9)所示,将其作为电压安全裕度。
(8)
(9)
式中:β为电压偏差量的置信水平;Φ-1( )为标准正态分布积分函数的反函数。
因此,通过改变电压安全裕度来控制电压越限风险,并将原随机优化模型转化为基于置信度的机会约束模型。
1.3 考虑不同电压裕度的优化方法
将不考虑风电预测误差且以网损最小为目标的系统无功优化称作初始优化,初始优化结果如图1绿色虚线所示。此时置信度β=0,部分节点将刚好抵达边界,将这部分节点称作电压关键节点,例如节点3。在初始优化的基础上加入风电预测误差,系统电压将出现不同程度的越限风险,如节点3电压幅值在β置信度下的越限值等于其置信区间半宽。

图1 方法1和方法2的电压可行域图Fig.1 Acceptable voltage ranges of method 1 and method 2
对此,提出3种控制电压越限的优化方法。
方法1:基于上述越界现象,系统无功优化时所有节点电压安全裕度都等于在β置信度下的最大电压越限值。如图1中蓝色虚线即方法1考虑电压安全裕度后的电压边界。
方法2:基于上述越界现象,系统无功优化时每个节点电压安全裕度等于β置信度下各自节点电压的置信区间半宽。如图1中橙色区域即方法2的电压安全裕度。
需要注意,方法1和方法2都是在初始优化点处得出的电压安全裕度,当风电预测误差较大时,会造成一定误差,因此提出方法3。
方法3:每次优化迭代,都基于当前状态求得对应的电压安全裕度。如图2中橙色区域表示方法3的电压安全裕度,即方法3所得电压安全裕度和电压约束条件将随迭代点的改变而改变。
图1和图2中置信度β用绿色区域面积表示,置信度越大,置信区间半宽和电压安全裕度就越大。在对输电网进行无功优化时,电压总是尽量升高来减少线路损耗,如图2和图3绿色实线所示。但配电网却不相同,在配电网轻负载时,无功优化将使系统电压尽量降低。
方法1和方法2相比,边界采用“一刀切”方式,未充分利用不同节点灵敏度不同的特点,因此优化结果比方法2更加保守;方法2和方法3相比,计算速度更快,在风电预测误差小时,计算偏差很小,但在风电预测误差较大时会引入较大误差,不如方法3准确。综上所述,提出根据风电预测精度来选择不同无功优化的方法,即:在预测精度较高时选用方法2进行优化,在预测精度较低时选用方法3进行优化。
需要注意的是,采用上述考虑电压安全裕度的方法将使实际运行更加安全。因为实际运行中图3蓝色部分的概率虽然在置信度β之外,但并未发生电压越限。事实上,电压的实际不越限概率应属于区间[β,(1+β)/2]。以无功优化后节点电压靠近上边界为例,当优化运行点离下边界的距离较近时约为β,离下边界较远时约为(1+β)/2。

图2 方法3的电压可行域图Fig.2 Acceptable voltage range of method 3

图3 单节点电压可行域Fig.3 Acceptable voltage range ofa node
2 无功优化模型
2.1 目标函数
以网损最小为目标函数,对系统进行无功优化。目标函数如式(10)所示,右侧第一项表示串联损耗,包括线损和变压器铜耗等;右侧第二项表示并联损耗,包括线路电晕损耗和变压器铁耗等,此处将线路电晕损耗整合到线路节点处。
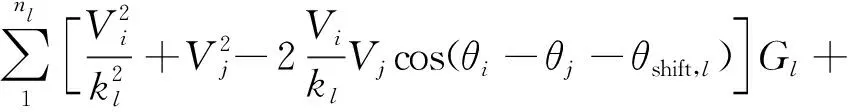
(10)
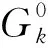
2.2 约束条件
约束条件包括等式约束和不等式约束。等式约束即所有节点的有功平衡方程和无功平衡方程[22],表达式分别为
Ceq(i)=Pgen,i′-Pload,i-Vi∑Vj(Gijcosθij+Bijsinθij)=0
(11)
Ceq(n+i)=Qgen,i′-Qload,i-Vi∑Vj(Gijsinθij-Bijcosθij)=0
(12)
式中:Ceq为模型的等式约束;Pgen,i′和Qgen,i′分别为第i′台发电机注入节点i的有功和无功功率;Pload,i和Qload,i分别为节点i负荷吸收的有功和无功功率;j为所有和i节点直接相连的节点序号;Gij和Bij分别为节点导纳矩阵中ij支路的电导和电纳;θij为节点i和节点j的相角差。
不等式约束包括变量约束和函数约束。所有支路输电容量不得超过其允许值,即
(13)
式(13)中:C为模型的不等式约束;l为支路序号;Sl和Sl,max分别为支路l流过的视在功率及其允许值。
同时,控制变量的约束为
(14)
(15)
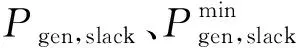
在含风电接入的电力系统中,要考虑一定置信度下的电压安全约束,即每个节点电压均需满足式(16)~式(19),表达式分别为
(16)
(17)
ΔVi=fV(ΔP,ΔQ,β)
(18)
Δθi=fθ(ΔP,ΔQ,β)
(19)
式中:Vi,min和Vi,max分别为节点i电压幅值上下限,分别取0.9 pu和1.1 pu;θi,min和θi,max分别为节点i电压相角的上下限,分别取-2π和2π;ΔVi和Δθi分别为节点i电压幅值和相角的安全裕度;fV和fθ分别为电压幅值和相角的安全裕度与风电预测误差及置信度的函数关系,可分别由式(2)~式(7)得到。
3 求解算法
3.1 模型转化与内点法求解
以上建立的优化模型本质上属于非线性规划问题,原问题可以描述为
(20)
式(20)中:f为目标函数;Ceq和C分别为等式和不等式约束;变量x由Pslack、Qi′、Vi、θi按顺序排列组成。
原问题中含有等式和不等式约束,可通过增加松弛变量,将不等式约束转化为等式约束。如对于第c个不等式约束,可增加变量sc>0,满足Cc(x)+sc=0,同时设置障碍函数μln(sc),当障碍系数μ由正无穷趋于0时,逼近于原问题。再通过引入拉格朗日系数,将等式约束问题转化成无约束问题,表达式为

(21)
式(21)中:s为所有松弛变量sc组成的列向量;λC和λCeq分别为不等式约束和等式约束的拉格朗日乘子行向量;通过式(20)到式(21)的转化,将原问题变为了无约束非线性规划问题。
内点法求解采用牛顿法来计算下一个迭代点,牛顿法计算前先判断当前迭代点的海森矩阵是否半正定,只有当海森矩阵半正定时,牛顿法在当前迭代才有效[23],如果当前迭代点的海森矩阵不是半正定,内点法将转而采用信赖域方法,在该信赖域内再使用共轭梯度法去求下一个迭代点[24],从而循环迭代求解直至最优运行点。上述求解过程详见文献[23-25]。
3.2 解析化梯度矩阵和海森矩阵的改进算法
在求解无功优化这一非线性规划问题时,原算法采用的有限差分法所得的近似梯度矩阵和海森矩阵往往不够精确,甚至相差较大,最终导致迭代次数多,求解速度慢。因此对其提出改进算法,采用解析化梯度矩阵和海森矩阵的改进算法,可大大节省运算时间,减少迭代次数,使结果更加准确和可靠。原算法和所提改进算法的性能对比请参见第4节。以目标函数为例推导其解析化梯度矩阵和海森矩阵,同理可得等式约束方程和不等式约束方程的梯度矩阵和海森矩阵。
目标函数的梯度矩阵Gf是一个(ng+2n+1)维列向量,如式(22)所示,Gf中各元素由式(23)求得。
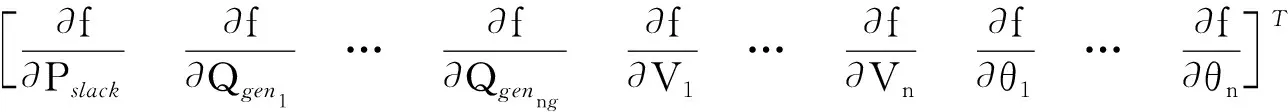
(22)
(23)
目标函数的海森矩阵Hf是一个(ng+2n+1)维方阵,如式(24)所示,Hf中各元素由式(25)、式(26)求得。

(24)

(25)
(26)
4 案例分析
4.1 案例一:含风电场的IEEE-39节点输电系统
对含风电场接入的IEEE-39节点输电系统进行无功优化,研究风电预测误差对电压的影响。如图4所示,节点36和38处有大型风场接入,风场功率预测误差引起的不平衡功率由平衡节点吸收。设节点36和38处风场的功率预测误差均服从均值为0,标准差为50 MW的正态分布,两个风场的相关系数为0.5。
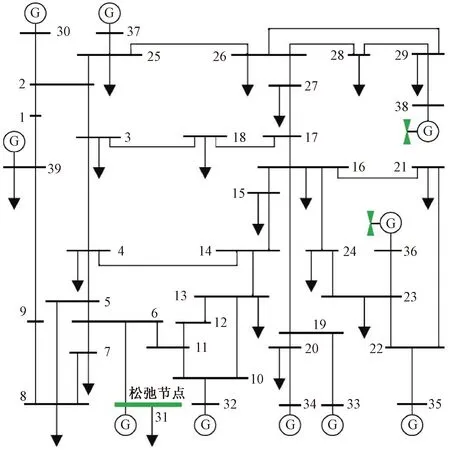
图4 含风电场接入的IEEE-39节点电力系统图Fig.4 IEEE-39 bus power system with wind farm access
如图5所示,最下方的蓝色曲线表示在无风电预测误差时,对图4中IEEE-39节点系统进行无功优化后各节点的电压幅值结果,即前文1.3节中介绍的初始优化。在此基础上加入风电预测误差后,观察不同置信度β下各节点电压的变化情况。图5从下往上共14组曲线,分别对应从小到大14种不同置信度β。由图5可知:随着置信度的逐渐增大,部分节点电压将陆续越限(即超过了1.1 pu),电压上升越快的节点表明该节点对功率变化越灵敏。同时,随着置信度的不断增大,电压关键节点逐渐发生转移,当置信度为0.95~0.99时,电压关键节点由{25,36}转变为{25,28,29},因为后者的灵敏度比前者大。
图6是不同置信度下节点电压相角的变化情况,可知电压相角始终在-20°~10°变化,无越限风险。
图7是在0.95置信度下,由前文1.3节所述方法1和方法2所得的各节点电压上下边界和无功优化后的节点电压幅值。表1为图7中方法1和方法2对应的上边界平均值和网损值。由图7和表1可知:方法2所得的电压上边界平均值比方法1更低,但无功优化后的网损值却更小,这是因为方法2中节点{19,22,35}的灵敏度比关键节点{25,36}低,其电压安全裕度相应更小,允许无功优化后节点{19,22,35}的电压比关键节点{25,36}更高,只要满足在风电预测误差下,节点{19,22,35}的电压值依旧小于1.1 pu。与方法1相比,节点{19,22,35}电压的提高有利于提升整体电压水平,从而使方法2网损值更小。
图8为不同置信度下由前文1.3节所述方法1和方法2优化所得网损曲线,可知随着置信度的增加,优化后系统的整体电压水平下降,网损值上升,且置信度越接近1,网损值增加越快。因为方法2无功优化后系统整体电压水平比方法1略高,所以其网损值始终更小,这也证明方法2比方法1更优。在0.95~0.99置信度下,该系统的电压关键节点逐渐发生转移,图5中{25,28,29,36}节点的电压越限值几乎相等,此时两种方法对关键节点的电压边界约束几乎相同,使得无功优化后的电压水平和网损值很接近。

图5 不同置信度下节点电压幅值越限图Fig.5 Bus voltage amplitude violation with different confidence levels

图6 不同置信度下节点电压相角变化图Fig.6 Bus voltage phase changing with different confidence levels

表1 方法1和方法2的上边界平均值和网损值Table 1 Upper boundary average and power loss by method 1 and method 2
由于节点25一直是关键节点,图9展示了其电压幅值与置信度和风电功率预测标准差之间的关系,可知其电压幅值随置信度的增加而减小,随风电功率预测标准差的增加而减小。风电场之间的相关系数同样会通过影响风电功率预测标准差来影响优化后的电压幅值。一般而言,相关系数越大,优化后的电压幅值越小。
表2对比了0.95置信度下方法1和方法2算法改进前后的性能,可知,采用解析化梯度矩阵和海森矩阵的改进算法可以提高求解效率。总的来说,改进算法的计算时长约为原算法的1/12,迭代次数约为原算法的2/5,引用函数次数约为原算法的1/171。
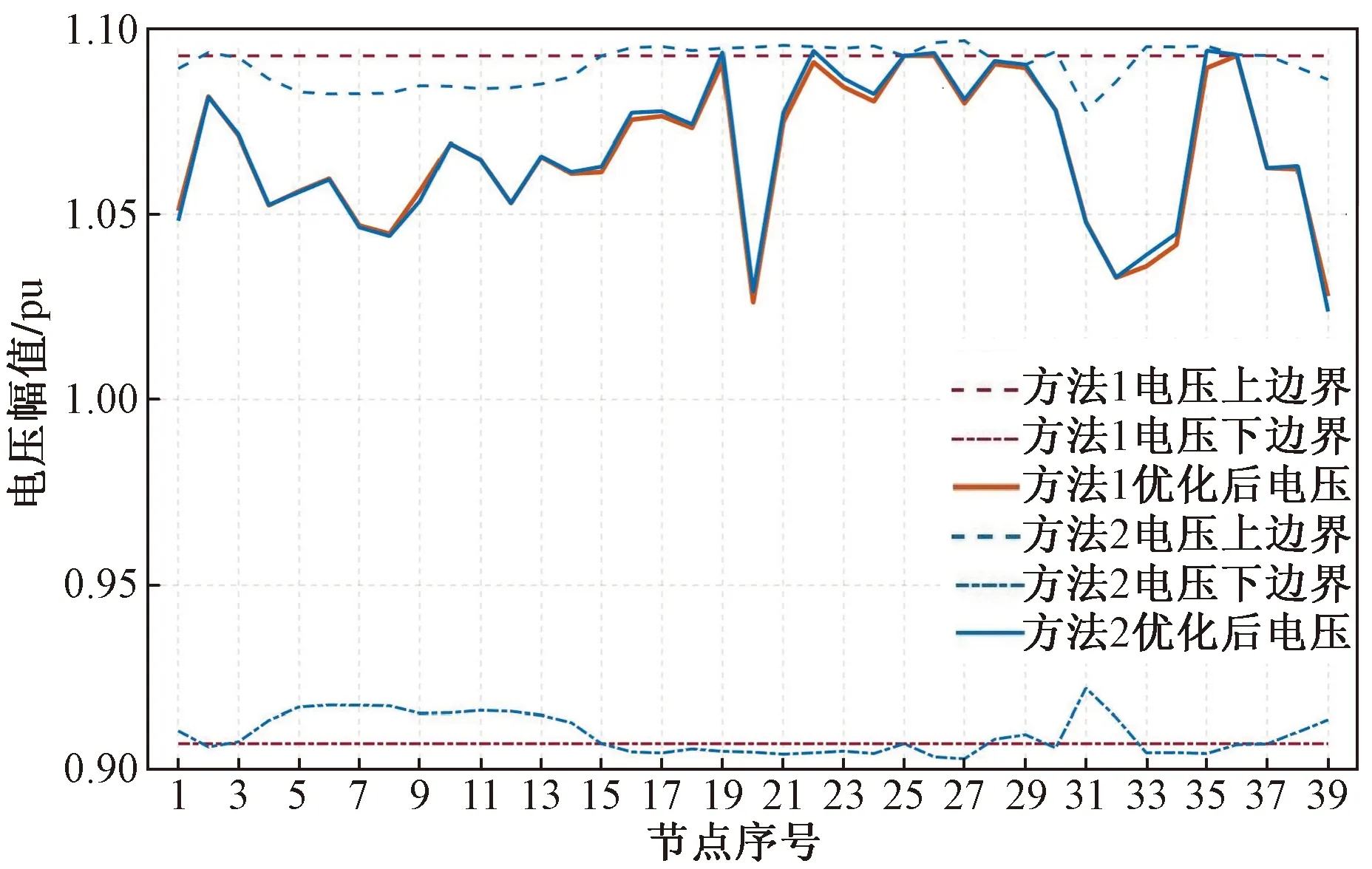
图7 方法1和方法2优化后电压图Fig.7 Optimized voltages by method 1 and method 2
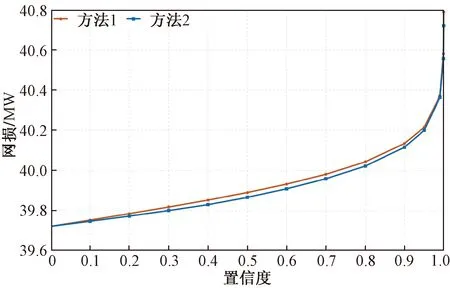
图8 网损值随置信度变化的曲线图Fig.8 Curves of power loss changing with different confidence levels
图10测试了在0.95置信度下,风电功率预测标准差分别为100 MW和150 MW时,方法2和方法3

图9 无功优化后节点25的电压曲面图Fig.9 Voltage surface of bus 25 after reactive power optimization
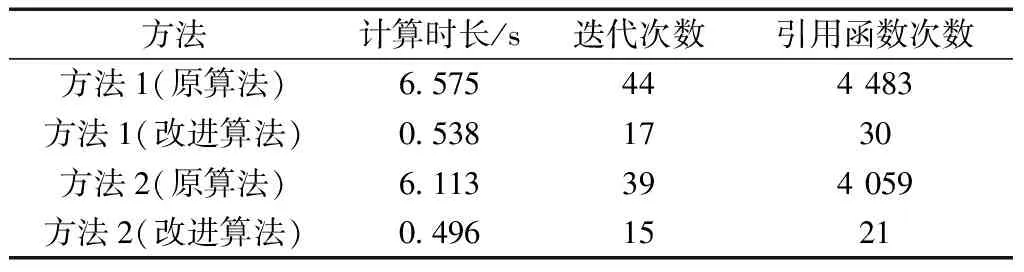
表2 算法改进前后性能对比表Table 2 Performance comparison before and after algorithm improvement
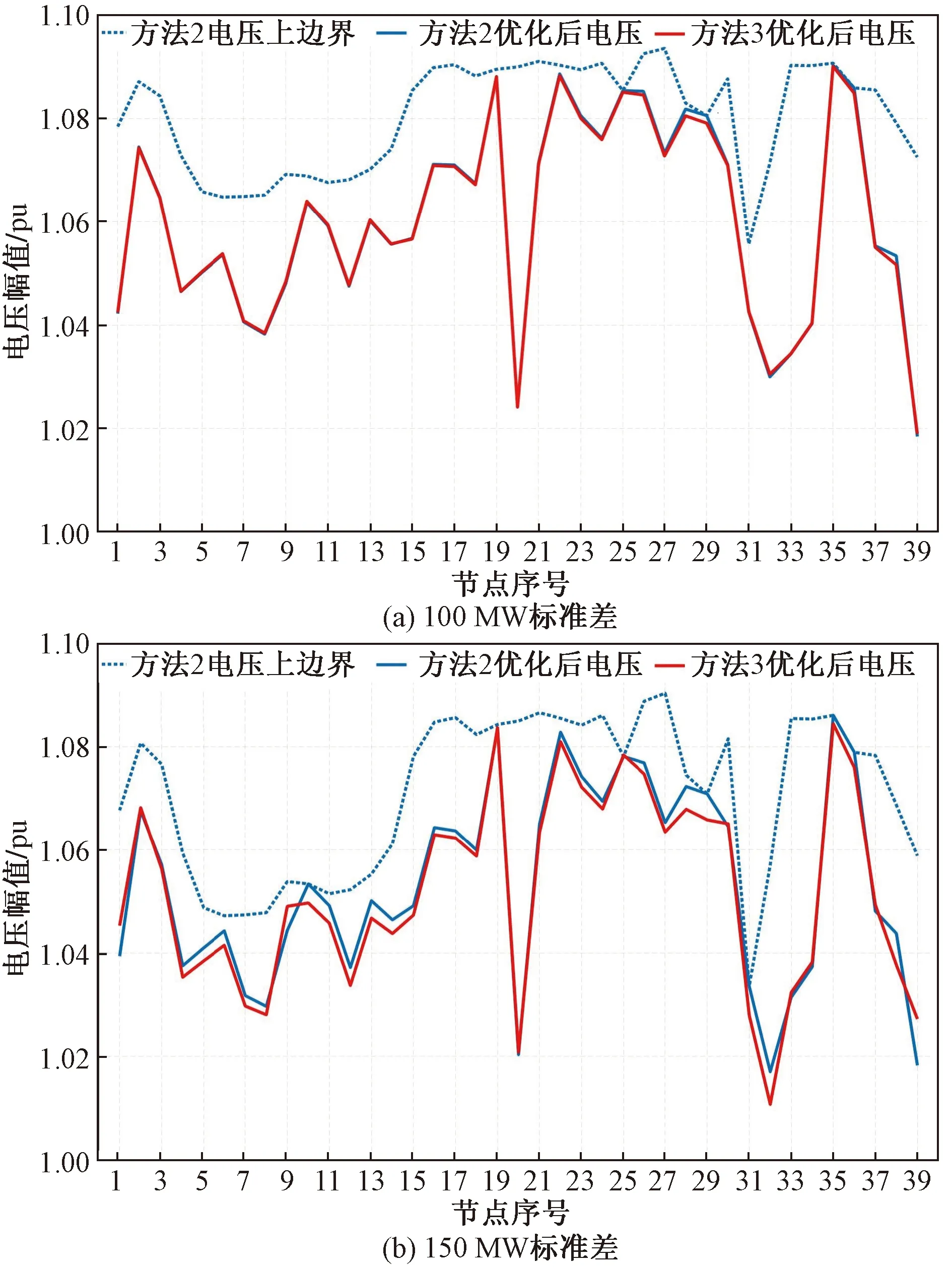
图10 在100 MW和150 MW标准差下方法2和方法3优化后电压图Fig.10 Optimized voltages by method 2 and method 3 with standard deviations of 100 MW and 150 MW
的无功优化电压幅值结果。可以看出,在风电功率预测标准差为100 MW时,方法2和方法3的无功优化结果差别很小,但当风电功率预测标准差为150 MW时,两者的无功优化结果差别较大,且方法3优化后的整体电压水平比方法2更低。主要原因在于,当风电功率预测误差变大,无功优化后的运行点将距离初始优化运行点更远,从而导致两种优化方法的灵敏度系数差别变大,而由1.3节介绍可知,方法3每次优化迭代都基于当前迭代点计算电压安全裕度,因此方法3的最终优化结果更加准确和符合实际情况,也更适用于风电功率预测误差较大的场景。同时,方法3优化后的整体电压比方法2更低,其电压幅值也更加安全,不易越限。
表3对比了方法2和方法3的计算成本和所得网损值,由此可知,方法3的计算时间、迭代次数和引用函数次数均多于方法2。这是因为在优化过程中,方法2的电压安全裕度是固定不变的,而方法3每次迭代都基于当前状态重新计算电压安全裕度,即由式(3)~式(9)求得电压安全裕度,再代入电压不等式约束式(16)和式(17)中,求解下一个迭代点,因此增加了求解的计算成本,同时方法3优化后的网损值略高于方法2。
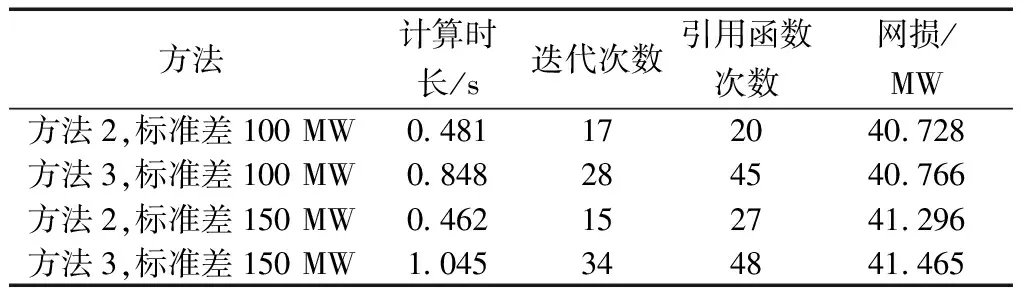
表3 方法2和方法3的计算成本和网损值Table 3 Computation cost and power loss of method 2 and method 3
综合以上分析可知,方法1的经济适用性不如方法2,因为方法1未充分利用各节点电压对功率变化灵敏度不同的特点,导致无功优化后的网损值比方法2更大;方法2适用于风电预测误差较小的工况,此时其计算偏差较小且计算速度较快;而方法3适用于风电预测误差较大的工况,虽然其计算成本增加,但其优化结果更加安全可靠,也更符合实际情况。
4.2 案例二:中国内陆某风场配电系统
为了验证所提方法的实际工程性能,本案例对中国内陆某风场配电系统进行无功优化。该风电场共有31台风机,每台风机的额定容量为2 MW且具有1.1倍的过载能力。该风电场根据地理位置可划分为3个区域,如图11所示。假设各风机出力相同,潮流计算时平衡节点电压为1.0 pu,采用风场出力比率(即风场出力和风场额定容量的比值)来衡量风场出力情况。
图12测试了该风电场网损值随出力比率的变化情况,可知风电场网损值将随着出力比率的增加而增加,且当风场出力较低或较高时,无功优化后的网损值比潮流计算所得网损值小得多,当风场出力中等时,两者相差很小,如绿色实线所示。这是因为风场出力较小时,网损以并联损耗为主,如表4中风电场出力比率为0.1~0.2时,无功优化使风电场吸收无功功率来降低系统电压水平,从而减小网损。当出力比率为0.4~0.5时,系统串联损耗和并联损耗相当,优化后系统电压水平和潮流计算时的电压水平较为接近,因此两者网损相近。当出力比率较高时,串联损耗占网损的主要部分,如表4中出力比率为0.6~1.0时,风电场发出无功功率,以提升系统电压水平和降低网损。出力比率为1.1时,风机出力达到容量上限,此时系统所需无功功率全部由平衡节点提供。
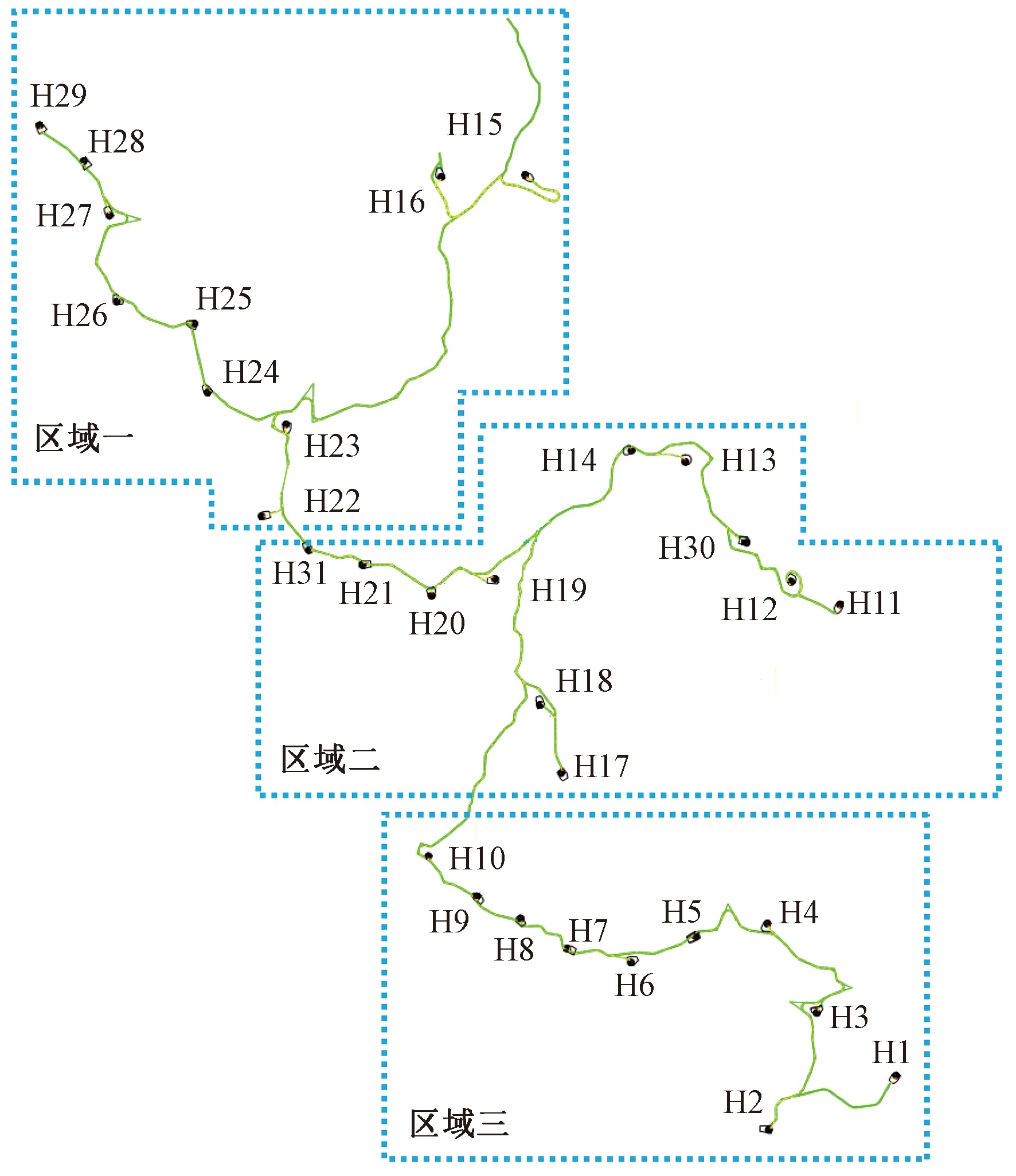
图11 某风电场的风机地理分布图Fig.11 Geographical distribution of the wind generators in a wind farm
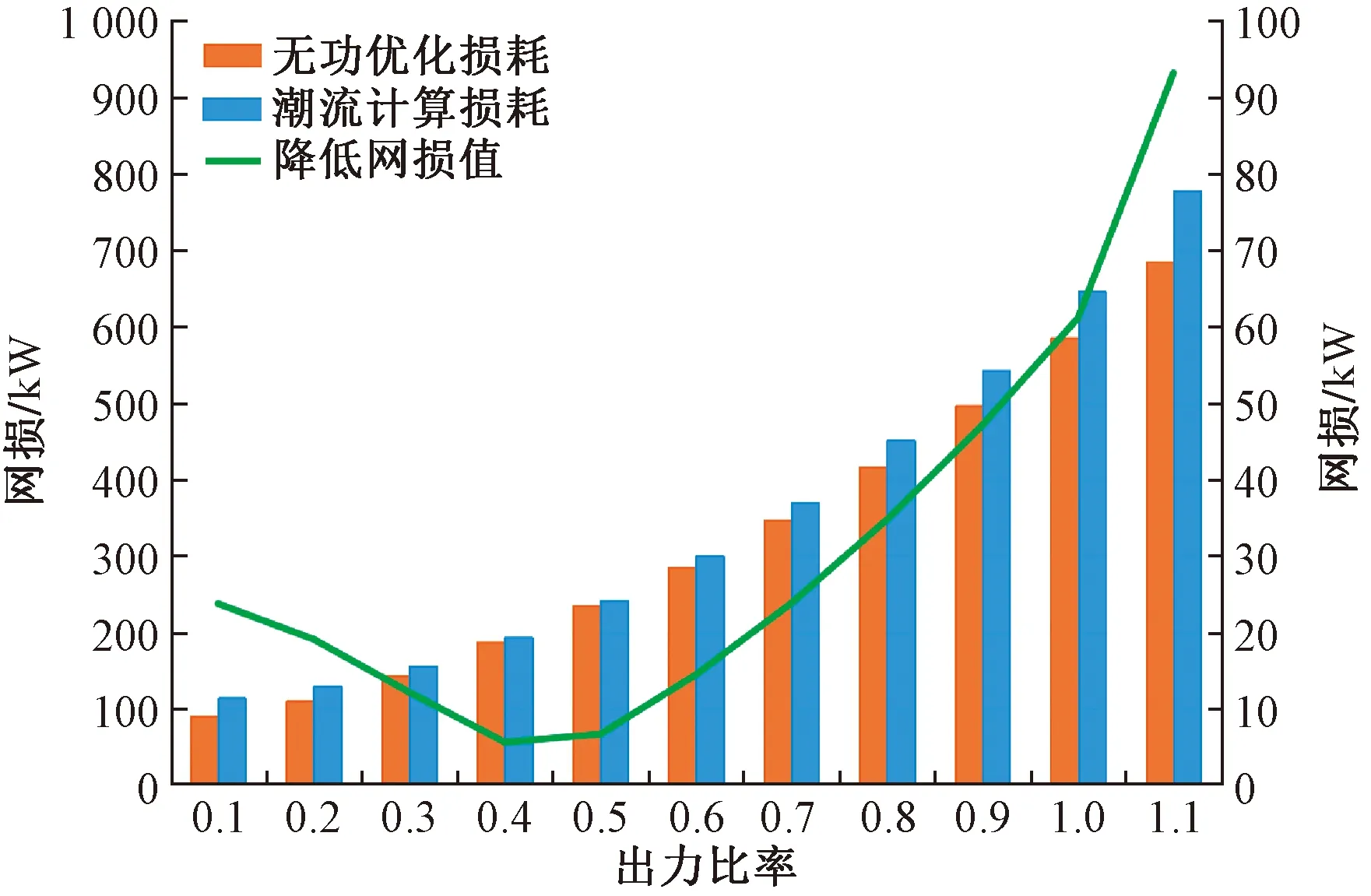
图12 网损值随风电场出力比率变化图Fig.12 Power loss changing with output rate of wind farm

表4 不同出力比率下风电场发出的无功功率Table 4 Reactive power generation by the wind farm with different output rates
在上述基础上,再考虑风电场的空间相关性,假设每个区域内部风机间的相关系数为1,相邻区域风机间的相关系数为0.8,不相邻区域风机间的相关系数为0.6,风机变压器变比为1.025。设风电功率预测误差的标准差为风电预测功率的1/10,在0.95置信度下,测试风场出力比率分别为0.3、0.45、0.6和0.9时的无功优化结果。
图13为优化后的节点电压图,由于节点1是孤立节点,在优化中不参与迭代,因此其电压始终为1.0 pu。节点4~34为风机变压器低压侧母线,节点35~65为风机变压器高压侧母线。当风场出力比率为0.3时,无功优化将使得整体电压靠近电压下限,节点34电压刚好位于下边界,是电压关键节点。当出力比率为0.45时,整体电压在1.0 pu左右,此时并联损耗对电压的梯度等于串联损耗对电压的负梯度,系统最优运行点在可行域内部,风电预测的不确定性对最优运行点的影响较小,系统能够承担较大的风电功率预测误差。当出力比率为0.6和0.9时,无功优化将使得整体电压靠近电压上限,节点37电压刚好位于上边界,是电压关键节点。由于出力比率为0.9时的风电预测不确定性大于0.6时,因此前者的整体电压水平较后者低。
系统的电压不均匀度也会影响无功优化结果,图13中,当风场出力较小时,节点35~65电压不能进一步降低,当风场出力大时,节点4~34电压不能进一步升高。如表5所示,当风机变压器变比ktr由1.025调整为1时,出力比率为0.3时的网损比调整前降低0.70%,出力比率为0.9时的网损比调整前降低0.28%。因此,合理地调整变压器变比,减小系统电压分布的不均度,能够进一步减小无功优化后的系统网损。
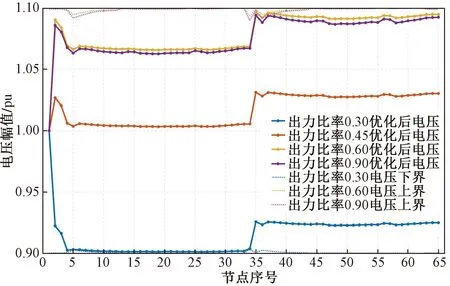
图13 风电场不同出力比率下的优化电压和上下边界Fig.13 Optimized bus voltages and upper/lower boundaries of the wind farm with different output rates
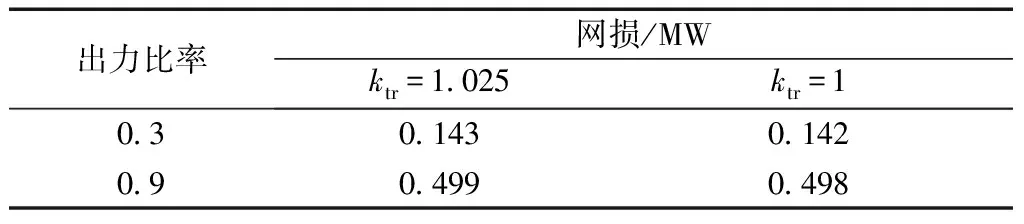
表5 不同出力比率和变比下的网损值Table 5 Power loss of the wind farm with different output rates and transformer ratios
5 结论
以网损最小为目标函数并考虑控制电压越限风险,提出一种基于置信度机会约束规划的风电场无功优化技术,来研究含风能接入系统的无功优化问题。主要得到以下三点结论。
(1)提出了考虑电压安全裕度的不同方法,并分析了它们各自的优缺点和适用工况。在风电预测精度较高时,方法2能提高计算速度;在风电预测精度较低时,方法3能保证系统运行安全性且更加符合实际情况。
(2)提出解析化梯度矩阵和海森矩阵的改进算法,与差分近似的原算法相比,大幅提高了求解效率。
(3)在输电系统或出力较高的风电场配电系统中,无功优化使系统电压尽量升高,在出力低的风电场配电系统中,使系统电压尽量降低,均有利于降低网损。此外,适当调整变压器变比能进一步降低网损。
一般来说,风电预测误差将随预测时长的增加而增大,未来将根据所提的无功优化方法,进一步研究含风电接入系统的多时段无功优化问题。
