相空间重构与差分进化算法-烟花算法-支持向量机结合的高压开关机械故障诊断方法
2022-07-28陈志华孙逸翀王紫薇柯强刘洋刘会兰
陈志华, 孙逸翀, 王紫薇*, 柯强, 刘洋, 刘会兰
(1.国网湖北省电力有限公司黄冈供电公司, 黄冈 438000; 2.华北电力大学电气与电子工程学院, 保定 071003)
高压开关作为电力系统重要的控制与保护设备,其控制回路、操作机构和储能机构密切配合执行储能、合闸和分闸动作,此过程体现了储能电机、传动齿轮,弹簧、拐臂、主轴、连杆和动触头之间能量传递[1],伴随的振动信号蕴含机械部件传动、触头分离与碰撞,电机旋转和弹簧伸缩储能等丰富状态信息,利用振动信号区分开关异常状态成为近年来国内外电气设备故障研究焦点问题[2-4]。
提取振动特征的主要方法有小波变换(wavelet transform, WT)、经验模态分解法(empirical mode decomposition, EMD)和相空间重构。小波变换分解过程需设置母小波、分解层、频带阈值及合适分解方法。EMD可自适应分解,但对于含有大量噪声和干扰的振动信号,区分有用信号、噪声和虚假分量却十分困难。互补集合经验模态分解[5-6](complementary ensemble empirical mode decomposition, CEEMD)是EMD的优化形式,通过添加互补白噪声有效解决模态混叠缺陷,再利用相空间重构[7]从动力学角度给出固有模态函数(intrinsic mode functions,IMF)分量的多维特征。
人工神经网络(artificial neural network, ANN)因泛化能力强多用于故障识别[8],但网络训练需大量样本数据,恰恰是高压开关类设备现场操作不频繁,导致故障数据样本非常少,影响了神经网络诊断准确性。基于统计学理论的支持向量机(support vector machine, SVM)实质是凸二次规划数学模型,在小样本故障分析中运算速度更快、精度更高[9]。SVM对初始参数敏感,何青等[10]利用果蝇优化算法优化核函数参数,提高分类效果。Xue等[11]将烟花算法(fireworks algorithm, FWA)运用到SVM寻优提高了诊断正确率,但烟花爆炸过程属于全局随机搜索过程,运行计算时间却大幅增加。
现利用差分进化算法(differential evolution,DE)加速FWA搜索过程,提出一种将相空间重构与DE-FWA-SVM相结合诊断高压开关故障方法。首先,采用CEEMD分解原始振动信号为若干频带信息,由相关系数筛选有价值IMF分量;其次,通过相空间重构将所选IMF序列映射到多维空间,计算李雅普诺夫指数和关联维数构成特征向量;最后,输入DE-FWA-SVM模型进行故障诊断实验。以期加速参数最优值的收敛,有效平衡分类器全局收敛能力和速度,对开关机械故障快速准确诊断具有应用价值。
1 振动信号特征提取
1.1 CEEMD算法
CEEMD是在EMD和总体平均经验模态分解(ensemble empirical mode decomposition, EEMD)基础上通过施加互补白噪声[12],不仅削弱了模态混叠现象,还克服EEMD集总平均次数较多问题[13],具体过程如下。
步骤1将一对互补白噪声ni(t)分别添加到原始振动信号x(t)中,得两种新信号,表达式分别为
Pi=x(t)+ni(t)
(1)
Ni=x(t)-ni(t)
(2)
步骤2对Pi、Ni分别进行EMD分解,得到j个IMF分量cj(t),即
(3)
步骤3重复步骤1和步骤2,在信号中加入新的正态分布白噪声序列,并将每次分解得到的IMF作为最终结果。
原信号经CEEMD分解得到一组不同频段的IMF分量,高频IMF中包含大量受采集环境影响的噪声干扰和分解出的虚假分量,不利于特征的提取,因此需对IMF进行筛选。相关系数是衡量分解信号与原始信号相关程度的指标,其值越大,表明相关性越好,该分量更能反映原始状态信息。利用相关系数保留价值IMF,并将相关系数较小的分量作为噪声和冗余分量舍去。
1.2 相空间重构
高压开关操动属于机构多部件能量传递的非线性振动,相空间重构能保证原动力系统几何不变性[14]。理论认为信号中任一状态分量都是由与之相互作用的其他分量决定[15],状态信息隐含在分量的演化过程中,故可从一个时域分量中复原出信号的所有特征信息。应用延迟坐标法[16]选取任一阶IMF分量Yi(t)经不同延时构造状态向量,重构相空间可表示为
Ym(n)={y(n),y(n+τ),…,y[n+(m-1)τ]}
(4)
y(k)=y(t+kΔt),k=1,2,…,N
(5)
(6)
式中:y(k)为k时刻离散化的系统值;τ为延时时间;m为嵌入维数;t为采样开始时刻;Δt为采样间隔;N为采样长度。
延迟时间τ和嵌入维数m的选择对相空间重构尤为重要,目前在参数选择上有两种观点[17]:一种认为两者不相关,τ和m可独立求解,常用方法有自相关函数法、互信息法和关联维数法;另一种认为两者相关,利用C-C算法可对τ和m进行联合计算,融合了自相关函数和互信息法的优点,在求解非线性模型方面有较大优势[18]。C-C算法的计算步骤如下。
步骤1根据延迟时间τ的不同,将振动信号的每阶固有模态分量序列{Yi(t)}划分为τ个不相交的时间序列S(m,N,r,τ)。

(7)

(8)
M=N-(m-1)τ
(9)
dij=‖yi-yj‖∞
(10)
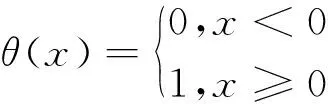
(11)
式中:dij为∞函数;r为搜索半径,取小于max(dij)的任意值;θ(x)为Heaviside函数;C(m,N,r,τ)为嵌入时间序列的关联积分。
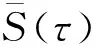
ΔS(m,N,r,τ)=max{S(m,N,r,τ)}-
min{S(m,N,r,τ)}
(12)
(13)
(14)
(15)
式中:nm为m个可能的取值;nk为k个可能的取值。
步骤3绘制S(τ)、ΔS(τ)及Scor(τ)的变化曲线,延迟时间窗口τw是在Scor(τ)取得全局最小值时对应的延迟时间,再根据式(16)计算嵌入维数m。
(16)
高压开关正常分闸时振动信号序列的参数结果如图1所示,S(τ)的第一个零点的横坐标为2.482,ΔS(τ)的第一个极值点为5,因此延迟时间τ=5。Scor(τ)在τ=5时取到了全局最小值,所以延迟时间窗口τw=5,嵌入维数由式(16)得出m≈2。相空间重构的嵌入时间序列的关联积分为0.837,搜索半径为r=10.804 2。由于重构相空间的冗余和奇异吸引子轨道拥挤程度会随这两个重要参数而改变[19],所以利用C-C算法得到的延迟时间和嵌入维数即为最优值。
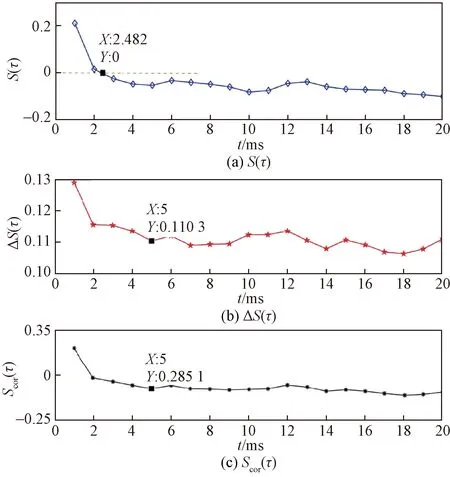
图1 固有模态分量序列的S(τ)、ΔS(τ)及Scor(τ)变化曲线Fig.1 S(τ) of natural mode component sequence, ΔS(τ) andScor(τ) of the intrinsic mode component sequence
1.3 提取相空间混沌特征
相空间直观图因振动信号时频分解长度不同存在波形相似的情况,不能直接定量反映非线性系统的本质特征,故引入最大李雅普诺夫指数[20]和关联系数[21]描述其动力学特征。
假设原信号经CEEMD分解为m阶IMF分量,再通过相空间重构计算李雅普诺夫指数T1=[T11,T12,…,T1m]和关联系数T2=[T21,T22,…,T2m]。T1和T2构成2m维特征向量T=[T11,T12,…,T1m,T21,T22,…,T2m]作为最终特征输入到优化后的支持向量机中进行机械状态识别。
2 DE-FWA-SVM的优化诊断算法
支持向量机的核函数参数g和惩罚因子C对分类效果影响较大[22],首先将最优参数C和g赋值给初始烟花,烟花算法通过模拟火花爆炸过程进行全局随机搜索,寻找适应度较好的烟花[23-25]。根据动态火花爆炸策略,差分进化算法增加烟花在最优值附近爆炸的数量,从而加快了烟花向适应度好的位置收敛的速度,提高了烟火在最优值附近的局部搜索能力[26]。
2.1 DE优化FWA步骤
步骤1在可行解范围内随机初始化n个烟花,并评估它们的适应度Y是否超过最大适应度Ymax。
Ymax=max[f(xi)]
(17)
式(17)中:f(xi)为该xi位置对应的适应度。
步骤2根据适应度计算每个初始烟花的爆炸火花数量Si和爆炸范围Ai。
(18)
式(18)中:A*为最大爆炸幅度;Ymin为当前烟花种群最优适应度;ε为常数;N3为种群总数。
步骤3对烟花进行差分变异。通过二项式杂交方法,生成p个差分变异火花。
(19)
式(19)中:k=1,2,…,D;krand为区域[1,D]上的随机数;CR为杂交概率。
步骤4评估爆炸火花和变异火花的目标函数值,根据动态爆炸火花策略调整火花数目。
步骤5从中烟花集合Ω中选择n个优质烟花进入下一次爆炸,直至满足迭代停止条件,个体被选择的概率为
(20)
式(20)中:fmax(xi)为烟花集合Ω中个体最大适应度。
2.2 核函数参数g和惩罚因子C的优化步骤
应用DE-FWA优化SVM模型中的惩罚因子C和核函数参数g,算法流程图如图2所示,参数优化步骤如下。
步骤1将惩罚因子Cmax和Cmin、核函数参数gmax和gmin赋值给初始烟花种群,随机初始化烟花的位置和速度,设置最大迭代次数。
步骤2计算烟花粒子爆炸火花数量和爆炸范围。

图2 SVM优化算法流程图Fig.2 Flow chart of SVM optimization algorithm
步骤3更新烟花,并计算爆炸火花的适应度是否在范围内,当满足迭代要求时烟花继续参与迭代,反之则被淘汰。
步骤4返回步骤2循环,当达到最大迭代次数时,返回值即为SVM惩罚因子C和核函数参数g的优化值。
3 试验及结果分析
3.1 高压开关测试试验
以ZN65-12型10 kV真空开关为研究对象,采集正常分闸、基座松动、转轴卡涩、开关拒动、弹簧疲劳5种工况下振动信号。通过木质卡件增加机构输出转轴阻尼模拟转轴卡涩,如图3(a)所示;使用垫片造成开关底座接地不平衡模拟基座不稳,如图3(b)所示;增大铁芯间隙阻止擎子撞击模拟产生拒动故障,如图3(c)所示;调节弹簧压缩量模拟弹簧疲劳,如图3(d)所示。采用YD-37压电式加速度传感器获得振动信号,每种工况各采集40组,共160组样本数据,训练样本和测试样本按1∶1的比例随机抽取。

图3 故障示意图Fig.3 Failure diagram
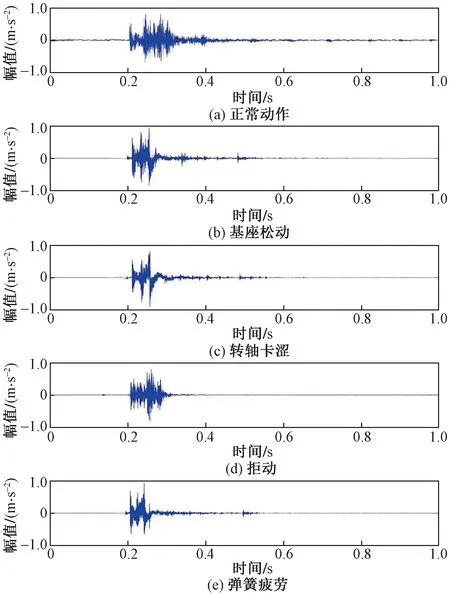
图4 5种振动信号波形示意图Fig.4 Five kinds of original vibration signals
采集到的某组振动信号时域波形如图4所示。可以看出,不同状态下高压开关的操动控制,部件间能量传递产生振动的时域波形差异并不明显,提取显著特征量和有效分类算法是准确进行故障诊断的关键。
3.2 振动信号特征提取
将时域信号经CEEMD分解到6个频带得到6阶IMF分量,如图5所示。各阶分量中包含主信号成分不同,根据相关系数筛选出每种状态最为合适的分量,相关系数值如表1所示。
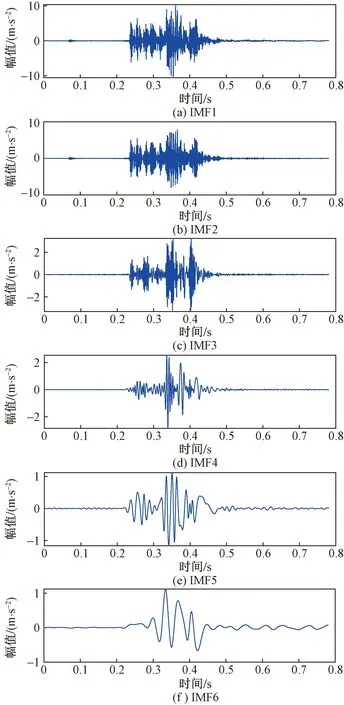
图5 振动信号的各阶固有模态分量Fig.5 Natural modal components of vibration signals
由表1可看出,所有状态下前三阶分量的相关系数均较大,在IMF4~IMF6中取最大值保留,另外两阶相关系数较小的分量视为噪声分量摒弃。因此,正常分闸和拒动保留IMF1~IMF4、基座松动、转轴卡涩和弹簧疲劳保留IMF1~IMF3和IMF6作为
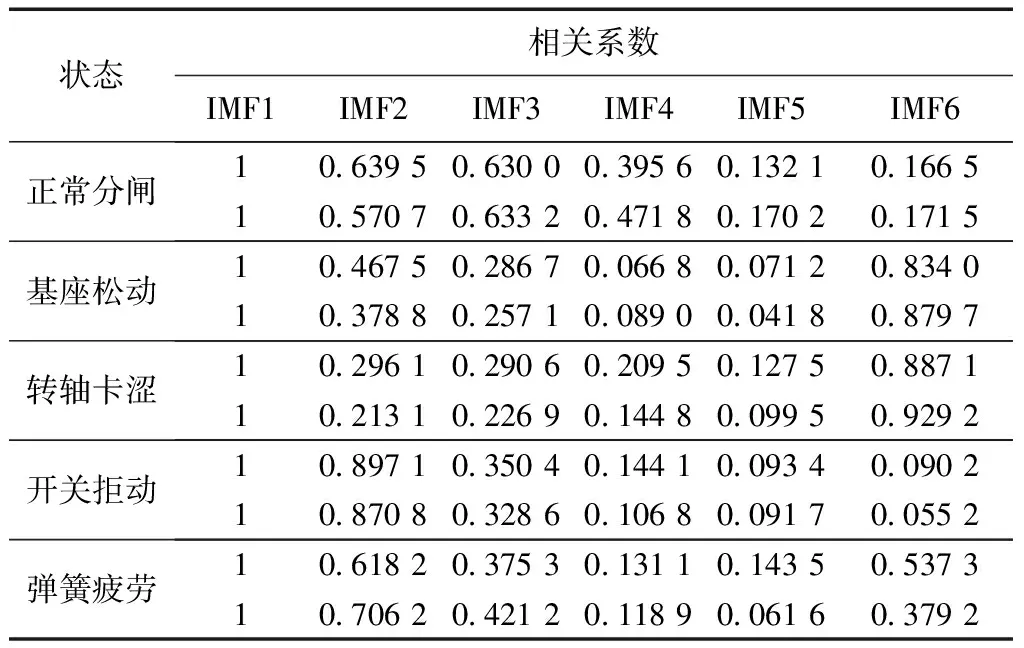
表1 不同工况下IMF分量相关系数Table 1 Correlation coefficient of IMF components under different working conditions
研究对象,筛选出的IMF分量通过相空间重构还原出信号动力学特性,并计算关联维数和李雅普诺夫指数。
关联维数采用饱和关联维数法(correlation dimension method, G-P),正常分闸时IMF2的lnC-lnr曲线如图6所示。关联维数D即为曲线中直线斜率值,由图1已算出相空间重构的嵌入维数m=2,故正常分闸的IMF2的关联维数为图6中拟合m=2时直线斜率0.056 9。
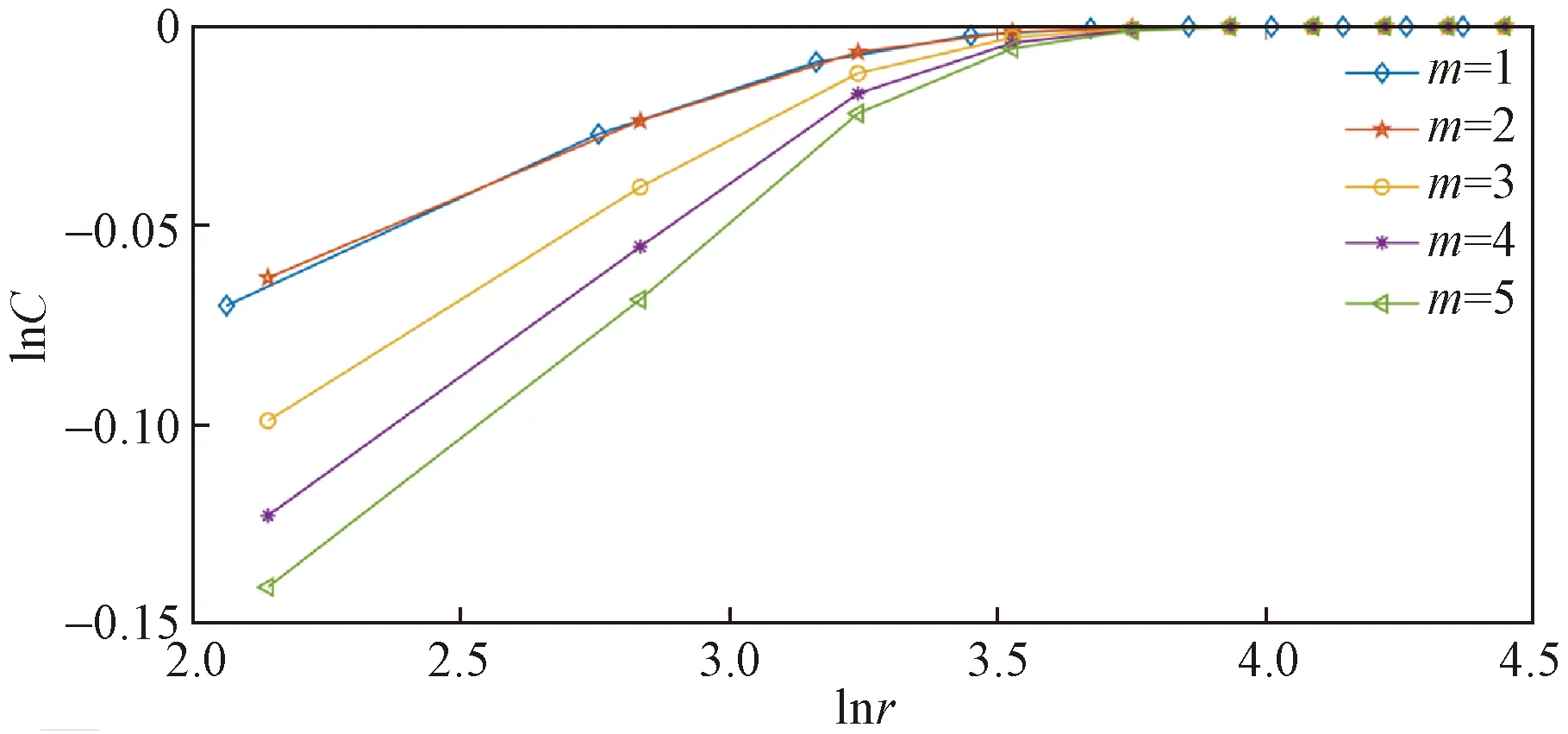
图6 正常分闸IMF2的lnC-lnr曲线Fig.6 lnC-lnr curve of normal opening IMF2
李雅普诺夫指数采用经典Wolf法,该指数是用于评价相空间收敛和发散程度的指数。表2是以5种工况下振动信号重构相空间的特征向量,T1为最大李雅普诺夫,T2为关联维数,取T1、T2为联合特征输入到分类器中进行识别。
3.3 基于DE-FWA-SVM的故障诊断
为验证本文方法的有效性,选用遗传算法(GA)、粒子群算法(PSO)、烟花算法(FWA)分别对SVM参数进行对比优化,烟花初始种群设置为20,最大迭代次数为200,图7为4种优化方式的诊断结果,表3为寻优所得核函数参数C和g的取值及算法迭代时间。可以看出,DE-FWA-SVM测试准确率高达98.75%,且在搜索域内能快速找到最优参数,相较于FWA-SVM快7.52 s,说明该算法迭代收敛能力更强,DE-FWA-SVM与FWA-SVM算法诊断对比结果如图8所示。图8中正常分闸样本标签为1,基座松动样本标签为2,转轴卡涩标签为3,拒动标签为4,弹簧疲劳标签为5。FWA-SVM有4个样本分类错误,其中2个基座松动被误分为正常,该情况称为漏报,在现场工作中,漏报往往比误判带来的危害更大。而DE-FWA-SVM仅一处转轴卡涩误分为拒动,分类准确率明显提升,且不存在漏报的情况,说明加入差分进化算法对FWA-SVM起到一定程度的优化作用,该方法从诊断时间和诊断效果两个方面都优于GA和PSO优化算法,在高压开关机械故障诊断中具有更高的分类特性。

图7 4种算法对SVM参数迭代对比Fig.7 Comparison of SVM parameters iteration by four algorithms
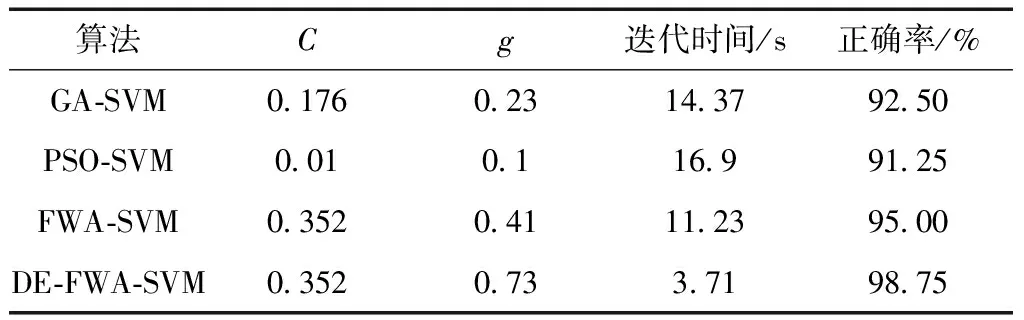
表3 4种算法对SVM参数寻优对比Table 3 Comparison of four algorithms for SVM parameter optimization
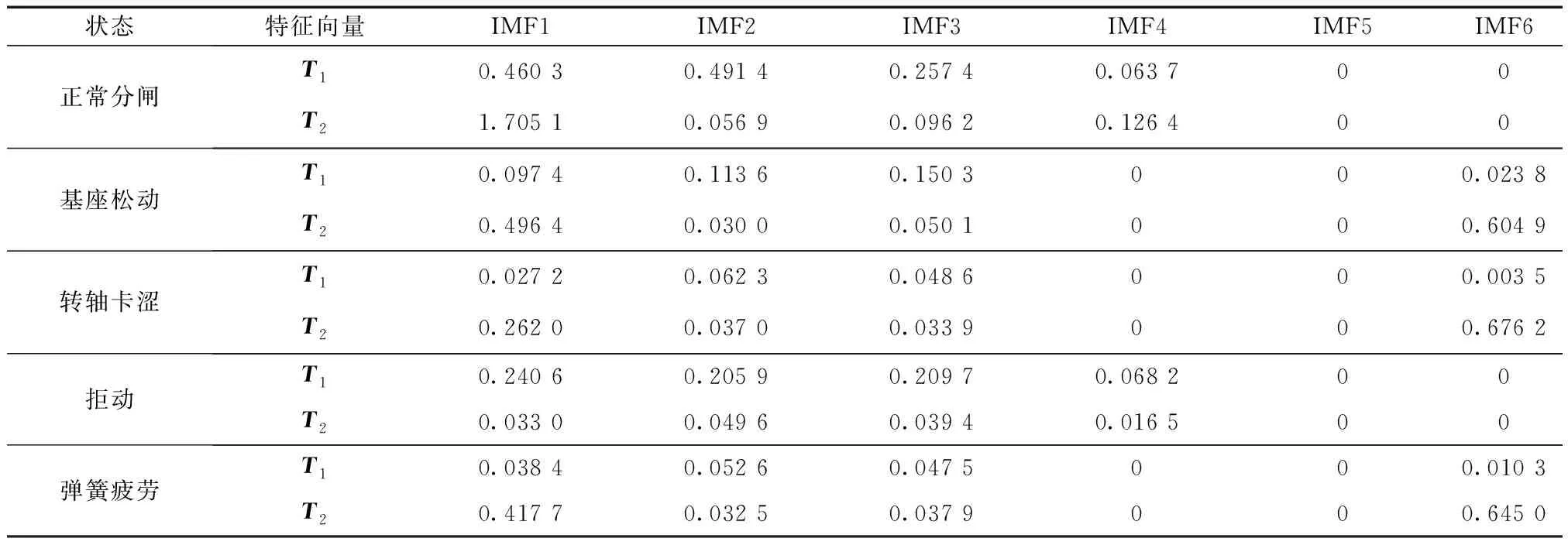
表2 重构相空间特征Table 2 Reconstruction of phase space features
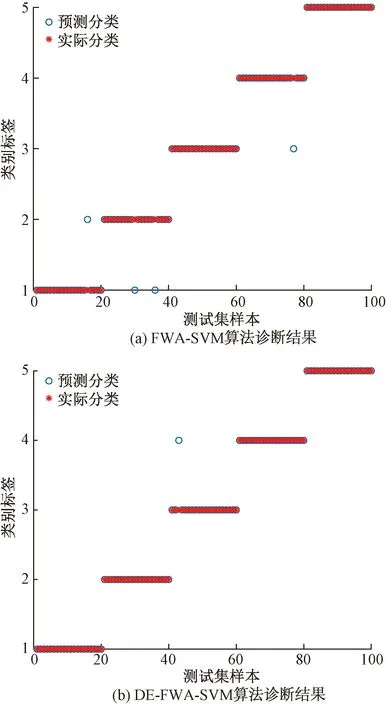
图8 FWA-SVM与DE-FWA-SVM算法分类结果对比Fig.8 Comparison of FWA-SVM and DE-FWA-SVM algorithm classification results
4 结论
振动信号可有效反映高压开关运行状态,提出一种基于差分进化FWA-SVM高压开关机械故障诊断方法。
(1)针对背景复杂振动信号的噪声干扰,通过CEEMD分解筛选相系数较大IMF分量保留有价值特征信息,结合相空间重构混沌特性解决了能量泄露问题。
(2)DE-FWA-SVM算法平衡全局搜索能力,同时加速了烟花向适应度高的位置收敛,大幅度提升模型的分类准确率。
(3)提出的振动信号系列处理算法原理上具有一定优势,目前限于现场高压开关故障数据较少,训练模型有待进一步优化。随着开关设备测试样本的累积和训练模型的完善,有望推广应用于故障诊断的工程实践中。
