考虑土体空间变异性的管廊基坑开挖过程中变形及能量演化特征分析

陈扬， 袁宗义， 梁禹

(1.天津大学管理与经济学部， 天津 300072； 2.中交第四航务工程勘察设计院有限公司， 广州 510290; 3.中山大学航空航天学院， 深圳 518107)

在岩土工程领域，土的变异性及其对岩土工程的影响已经得到广泛的认识[1-2]。天然岩土体由于受沉积、后沉积、化学风化、物理降解、水热变化和搬运等长期地质成因作用以及不同荷载历史的影响，导致岩土工程中存在固有的岩土不确定性。传统上对于岩土参数的不确定性建模的方法采用随机变量模型，该模型是将土体参数视作单一随机变量，从概率的角度描述参数的不确定性，但对于真实岩土体即使均质土层中不同位置处的参数也会不同，随机变量模型不能描述参数的空间变异性[4-7]。Cornell首次将土体参数视作随机场，Vanmarcke在其基础上进一步完善并发展了随机场理论在岩土工程中的应用，随后通过国内外诸多学者的持续探索，随机场理论被认为是表征土体参数空间变异性最有效的工具[4-7]。目前，随机场理论在边坡工程稳定性分析和地基承载力问题中的应用相对成熟，针对基坑开挖施工问题，目前相关的文献报道较少，易顺等[8]采用随机场描述基坑的土体刚度参数，研究了土体空间变异性对地表沉降和侧向位移的影响。郑俊杰等[9]采用随机场理论描述被动加固区水泥土的空间变异性，并建立了数值模型进行分析，通过对比随机性分析与确定性分析的结果发现水泥土的参数空间变异性对基坑变形的影响较为有限。上述关于随机场理论在基坑工程中的应用缺乏考虑不同施工步骤的影响，此外，大部分研究是基于单一土层的简单算例进行随机场模拟的，对实际工程中复杂多层土的基坑随机场理论的应用工程较少。

基坑的失稳实质上是土体及支护结构材料在外力、环境等因素的影响下发生破坏，材料发生破坏的本质是在能量的驱动下发生的。谢和平等[10]基于大量的土力学试验研究了岩土体破坏变形过程中能量的演化机制，构建了岩石的能量破坏准则。Tu等[11]基于能量守恒原理针对边坡的失稳判据开展了研究，提出了以弹性应变能突变、耗散能突变、重力势能突变、动能突变均可作为边坡失稳的判据。卢峰等[12]、周子涵等[13]也都从能量角度研究了边坡稳定性分析的问题。上述研究的局限性在于没有考虑岩土材料的空间变异性，针对于此，Huang等[14]在边坡失稳判据研究的过程中增加了空间变异性的研究，但该研究是仅考虑了单一土层的随机场模型，且未研究施工步骤的影响。另一方面，上述从能量守恒角度的研究均是以边坡稳定性分析这一问题开展的，关于基坑开挖这一常见的岩土工程问题鲜有探索。

综上所述，目前随机场理论在基坑开挖问题的应用中，缺乏考虑复杂多层土体空间变异性及实际开挖施工步骤的影响，且基坑开挖过程中的能量演化过程有待探究。有鉴于此，现依托佛山市某综合管廊基坑开挖工程开展，建立复杂多层土的随机场模型考虑土体参数的空间变异性，基于FLAC建立基坑开挖的二维有限差分模型考虑施工过程中基坑的变形特征，在此基础上研究随机场基坑开挖过程中的能量演化特征。

1 土层随机场及能量分布形式

1.1 土体参数随机场

在岩土工程中，随机场理论是一种用于表征岩土参数的空间变异性的数学模型。从概率学的角度出发，随机场理论是随机过程这一概念在空间上的推广。在随机场建模过程中，需要的参数主要包括随机变量的均值、方差、自相关函数、波动范围和随机变量服从的分布类型。采用中心点法建立土体参数随机场模型[14-15]，其步骤如下。

步骤1建立一个标准正态随机样本矩阵。采用拉丁超立方抽样方法得出标准正态随机样本矩阵ξ，ξ={ξ1,ξ2,…,ξn}。其中n表示随机场单元的数目。

步骤2求解相关系数矩阵的下三角矩阵。自相关系数矩阵C由随机场不同单元之间的自相关系数组成。对矩阵C进行乔列斯基分解C=LLT，得出下三角矩阵L。

(1)

(2)

式中：τ1和τ2分别为随机场中任意两个单元的中心点在水平和竖直方向上的相对距离；ρ(τ1,τ2)为随机场的二维自相关函数，选用指数型函数[16]；δx和δy分别为随机场水平方向与竖直方向的波动范围。

步骤3根据式(3)建立相关标准高斯分布随机场HD(x,y)。

HD(x,y)=Lξ

(3)

式(3)中：(x,y)为随机场空间点的位置坐标；L为自相关系数矩阵C分解得出的下三角矩阵。

步骤4建立相关非高斯分布随机场。在实际工程中，土体参数一般服从非高斯分布，通过等概率变换方法，将相关标准高斯随机场转换为相关非高斯随机场。对相关标准高斯随机场取指数，得到对数正态随机场Hi(x,y)。

(4)

式(4)中：μlni和σlni分别为相应正态变量lni的均值和标准差。转换关系如式(5)所示。

(5)

式(5)中：μi和σi分别为对数正态变量i的均值和标准差。

1.2 土体能量分布

在考虑能量守恒进行岩土工程的相关研究中，Tu等[11]、Huang等[14]对于边坡开展的稳定性研究的基本假定为：边坡在忽略外部环境温度等影响的情况下，仅考虑土体自重作用。此时，边坡体系的能量平衡方程简化为

ΔUg=ΔUd+ΔUe+ΔUk

(6)

式(6)中：ΔUg、ΔUe、ΔUk、ΔUd分别为重力势能减少量、弹性应变能增量、动能增量、耗散能(塑性应变能)增量。其中，单元体的重力势能ug、弹性应变能ue、动能uk分别为

ug=ρgh

(7)

(8)

(9)

式中：σ1、σ2、σ3分别为单元体3个主应力方向的应力；ε1、ε2、ε3分别为单元体3个主应力方向的应变；ρ为土体单元密度；g为重力加速度，取9.8 m/s2；h为土体单元质心点的高度；v为土体单元的速度。

不同于上述边坡稳定性分析问题，研究的对象为考虑施工过程的基坑开挖工程，基坑工程在施工荷载等外力作用下，其岩土体的内部的能量也在发生变化，外力对基坑所做的功主要转化为可释放的弹性应变能及耗散能。随开挖施工的进行，土体单元会产生位移及速度，因此也会产生一定的重力势能及动能的变化。由于采用的模型分析为静力分析，其产生的速度极小，因而产生的动能也很小，不具备实际物理意义。此外，研究模拟了施工开挖，开挖部分土体单元的能量将直接消失，这表明基坑开挖问题并非一个封闭的体系，因而不满足式(6)中的能量守恒，研究目的也仅限于探索针对基坑开挖这一施工过程中能量的演化情况。由于采用FLAC软件进行建模，其强大的fish语言提供了便捷的编程环境，对于各类能量的求解也将基于fish语言直接编程求解，需要指出，基坑的耗散能是由于发生塑性变形而消散的能量，岩土体的耗散能主要是塑性变形或损伤等形式[10]，因而采用塑性应变能代替前述的耗散能进行研究。

2 应用实例研究

结合前面的土层随机场建模及能量分布，依托佛山市某综合管廊基坑这一实际工程进行研究，采用FLAC软件建立管廊基坑开挖的有限差分模型，基坑土体的随机场模型将在MATLAB中进行建模，通过FLAC的fish语言实现参数随机场的导入及基坑土体单元能量的求解。

2.1 管廊基坑有限差分模型建立

2.1.1 工程概况

依托佛山市某综合管廊基坑项目开展，拟建场地沿线地上地下大部分地段未发现有地下管线设施经过，仅在穿越或跨越的现状道路及居民区地段发现有架空线路或地下管线设施经过。拟建道路场地周边路网密集，交通较好，施工条件一般。管廊基坑宽6.7～11.7 m，开挖深度为6.784～10.668 m。其场地土层从上而下依次为填土层、淤泥质土层、粉细砂层、粉质黏土层和强风化泥岩层。根据基坑的深度和场地地质资料及周边场地情况，管廊基坑支护主要采用钢板桩和横向钢内支撑结合的方式，开挖深度小于7 m时，采用15 m拉森IV新型钢板桩+2道钢支撑。钢支撑直径500 mm，壁厚为12 mm的钢管，钢支撑水平间距为4 m。

2.1.2 模型概况

根据上述工程资料，选取其中的典型断面进行建模计算，由于工程的管廊基坑较长，基坑的横断面尺寸远小于长度，因此可采用二维平面应变模型模拟基坑的开挖，从而简化计算。图1给出了管廊基坑支护结构断面、计算简图及建立的有限差分模型，图1(a)是典型断面的支护结构图，图1(b)是根据实际基坑结构进行一定程度简化得出的计算简图，图1(c)给出了基坑的二维有限差分网格模型，模型尺寸为35 m×20 m，开挖区域7 m×7 m，并标记出地面测点(S1～S6，间距2 m)和土体深部测点(D1～D6，间隔为3 m)。有限差分网格采用均匀网格进行划分，网格单元尺寸为0.5 m×0.5 m，本基坑模型共有2 800个土体单元。其中开挖区域有196个单元。图1(d)表示管廊基坑的开挖步序，本模型采用4个施工步(①～④)进行模拟。

步骤1进行钢板桩施工，开挖至第一层支护标高下面0.5 m处，进行第一道钢支撑施工。

步骤2开挖至第二层支护标高下面0.5 m处，进行第二道钢支撑施工。

步骤3开挖至坑底，并进行底部混凝土板施工。

步骤4拆除两道横支撑。其中，钢板桩采用Liner单元模拟，钢支撑采用Beam单元模拟。

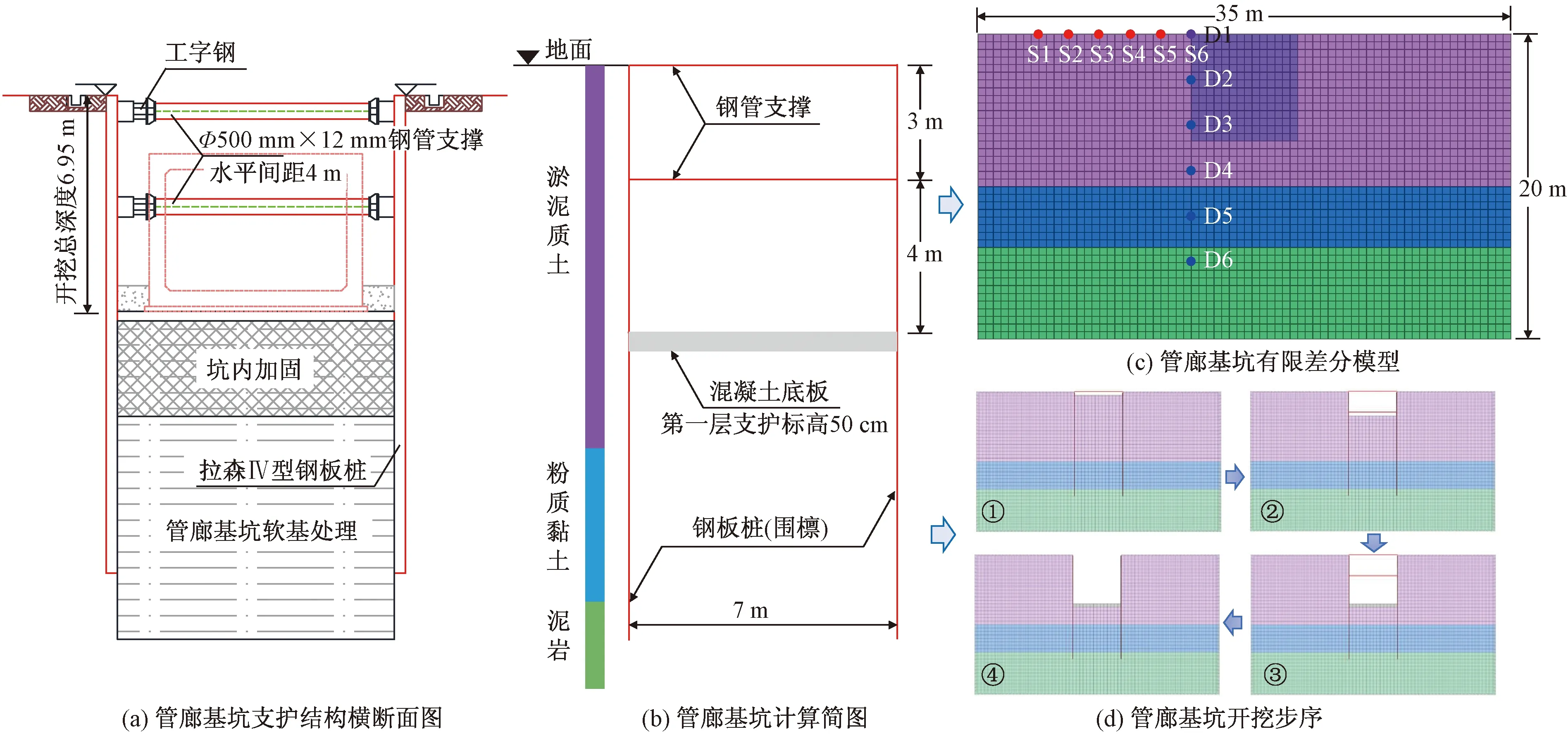
图1 管廊基坑支护结构断面、计算简图、有限差分模型及施工步序Fig.1 Support structure, schematic diagram, finite difference model and construction steps of tunnel foundation pit

不同于传统的基坑开挖施工有限差分模型，建立的模型需要考虑两个新的要素。

(1)岩土参数随机场的输入。基于式(1)～式(5)在MATLAB软件中建模获取参数随机场的n次实现结果，并存成n个txt文本，然后通过FLAC软件的fish语言编制参数读取函数，将每个随机场的txt文本的参数值分配到对应的单元中进行计算。

(2)基坑土体能量的输出。基于式(6)～式(9)进行基坑土体单元的能量求解，即记录所有土体单元的速度、位移、应力以及应变，然后进行计算。对于弹性应变能和塑性应变能，FLAC软件可以通过set mechanical energy on命令来直接记录计算过程中每个单元的这两种能量。基于上述步骤可以建立考虑能量演化特征的随机场-有限差分耦合计算模型。

模型中土体采用的本构模型为摩尔库伦模型，鉴于实际的土层过多且部分土层性质类似，因此对土层进行适当的合并简化，并对各个土层的参数进行合理的修正，其土体参数如表1所示。表1中的弹性模量在FLAC软件中需要转化为体积模量和剪切模量分别进行输入。

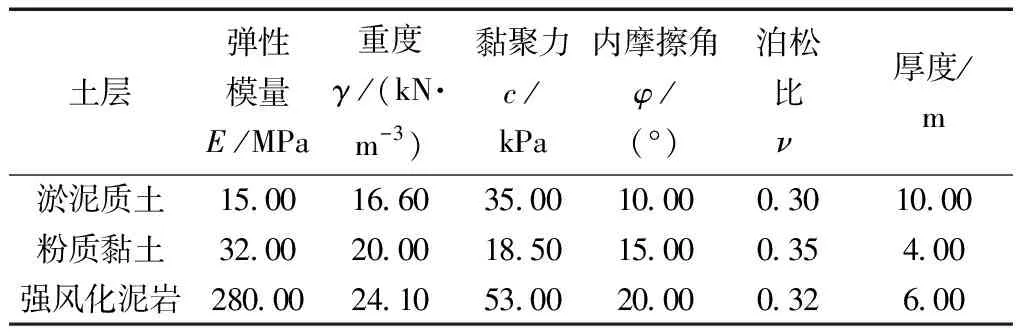
表1 基坑土体物理力学参数Table 1 Physical and mechanical parameters of foundation pit soil

2.2 管廊基坑随机场的实现及验证

2.2.1 多层土体随机场模型的实现

在诸多土体参数中，弹性模量空间变异性对于土体变形的影响相对较大。因此，将选取弹性模量进行随机场建模，其模拟过程在2.1节中已经给出，由于本模型含有3个土层，需要针对每个土层分别建立随机场模型，其模拟需要的参数如表2所示。

采用MATLAB进行随机场模拟，并随机抽取某次随机场的实现进行绘图如图2所示，不同颜色表征了不同位置处的弹性模量数值不同，可以借助右侧的色度条进行弹性模量数值的观察。可以看出，各个土层弹性模量的分布呈现明显的成层的特征，这是由于水平相关距离的长度远大于竖直相关距离所致。此外，采用的随机场网格尺寸与图1中有限差分模型的网址尺寸一致，均值0.5 m×0.5 m，这便于将随机场参数导入有限差分模型中进行数值计算。

表2 基坑土体弹性模量随机场统计参数Table 2 Random field parameters for the elastic modulus

图2 管廊基坑多层土体弹性模量随机场的典型实现Fig.2 Typical realization of elastic modulus random field of multilayer soil in pipe tunnel foundation pit

2.2.2 随机场模型验证

为验证上述建立的随机场模型的准确性，通过选取土层某一位置处随机场参数进行统计分析，随机场抽样次数为1 000次。从表2中看出，粉质黏土层和泥岩层所取的变异系数较大，因此选定这两层土的随机场进行验证，将这两层土弹性模量随机场的均值、变异系数随抽样次数的变化曲线绘制在图3中。随模拟次数的增加，粉质黏土及泥岩模量的均值及变异系数逐渐稳定，收敛于表2中随机场参数的给定值，这验证了所建立的随机场模型的准确性。

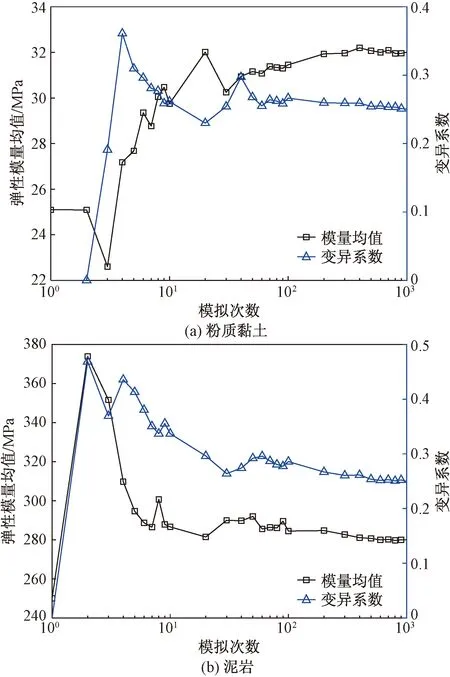
图3 粉质黏土层及泥岩层弹性模量随机场的验证Fig.3 Verification of Young’s modulus random field of silty clay and mudstone

2.3 考虑空间变异性的基坑施工变形分析

在管廊基坑的有限差分模型及随机场模型构建完成的基础上，将弹性模量随机场分配至对应的网格单元进行随机场-有限差分数值模拟计算，研究考虑弹性模量的空间变异性对于基坑施工过程中变形的影响。此前，需要建立传统的均质模型进行计算，用以与随机场模型的结果进行对比。图4给出了基于均值模型计算得出的开挖完成后基坑总位移云图及位移矢量图，可以看出，基坑的变形主要表现为隆起变形，最大值出现在基坑底部。基坑两侧均有指向临空面的水平变形，总位移的最大值约为20 mm。

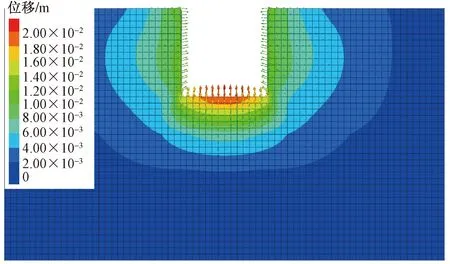
图4 开挖完成后基坑总位移云图及位移矢量图Fig.4 Total displacement nephogram and displacement vector diagram of foundation pit after excavation

将基于随机场理论生成的1 000次土体弹性模量分别导入有限差分模型中进行计算，记录图1中标记的地表变形测点(S1～S6)及深部变形测点(D1～D6)的不同施工步下的位移数据，绘制成图如图5和图6所示。图5给出了地表测点的不同施工步下地表测点总位移。可以看出：在前面3个施工步中，地表变形总体较小，总位移均在5 mm以内，说明采用的支护方式对地表变形起到了较好的控制作用。第四个施工步引起的地表变形明显增大，这表明两层钢支撑的拆除对基坑地表变形的影响较大。施工步2与3最大变形的测点出现在S5点，施工步1和4则出现在S6点，分析其原因，这是由于施工步2和3均为较大范围的开挖，引起两侧土体内部的应力重分布从而产生变形，但由于第一道钢支撑及钢板桩的存在限制了S6点的变形。

图5 不同施工步下地表测点总位移Fig.5 The total displacement of surface measuring points under different construction steps

图6给出了不同施工步下深部测点的水平位移变化规律，可以看出，深部测点的水平变形大部分为正(指向临空面方向)，仅在较深的测点(D5、D6)处存在负值。随基坑开挖施工的进行，深部水平位移的最大值依次出现在D2、D3、D4测点，这表明随基坑开挖深度的增大，对土体变形的影响范围越来越广。基坑开挖过程中，D6点的水平变形始终处于较小的范围(1 mm以内)，这对应的是钢板桩底部的位置，结果表明采用15 m的钢板桩能够对基坑起到有效支护作用。对于施工步3和4可以发现，两者的水平位移差别较小，说明两道钢支撑的拆除对深部测点的水平变形影响很小，也验证了所采用的支护方式能满足基坑稳定性的需求。

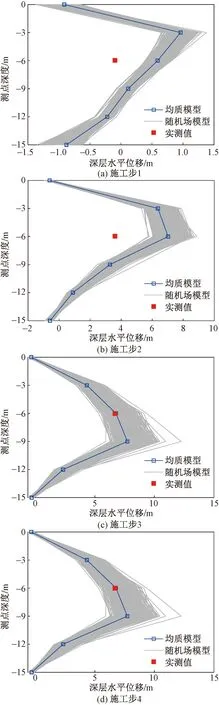
图6 不同施工步下深部测点水平位移Fig.6 Horizontal displacement of deep measuring points under different construction steps

为进一步验证所建立模型的准确性，将实际施工过程中各个施工步对应的位移实测值(图6中红色方块)与数值计算的结果进行对比，测点D3是实际工程与模型设置相重合的测点。对比D3测点的3种水平位移值可以发现，相对于实测值，传统的均质模型计算得出的位移偏小，但基本在同一量级且变化规律类似，这验证了基坑有限差分计算模型的准确性。此外，各个施工部的实测值基本能够在随机场模型的覆盖中，这也从实际工程中证明了随机场模型的优越性，避免了由于传统均质模型计算结果偏小而导致不安全的支护结构设计。随机场模型由于能够真实刻画土体参数的空间变异性，从而使得最不利的工况能够得以呈现，保证工程的设计及施工安全。

基于随机场模型的基坑施工有限差分模拟系统研究了基坑地表和深部的变形特征，与均质模型结果进行对比，其变化趋势基本一致，即多次随机分析的结果将均质模型结果包络在其中，可以将均质模型视作某次特殊的随机场模型的实现。从图5和图6中可以看出，不同测点处的灰色带宽差别较大，这意味着不同测点处的变形分布范围差别较大，变异性较大的区域需要重点关注。随机场模型充分考虑了土体参数的空间变异性，以变形特征为例，基于随机场模型得出的某个测点的变形并非确定的值，而是一组随机变量，可以理解为该测点可能发生变形的取值范围，还可以基于某点的变形量的随机分布结合规范的限值获取基坑的失效概率，这为基坑的设计施工提供了更有价值的考量。上述考虑空间变异性的基坑开挖模拟得出地表最大变形值为14.13 mm，深部最大水平位移为12.45 mm，均小于《建筑基坑监测技术规范》(GB 50497—2009)中的变形限值，这表明现有的支护方案能够满足基坑开挖的安全性要求。

2.4 考虑空间变异性的基坑施工能量演化研究

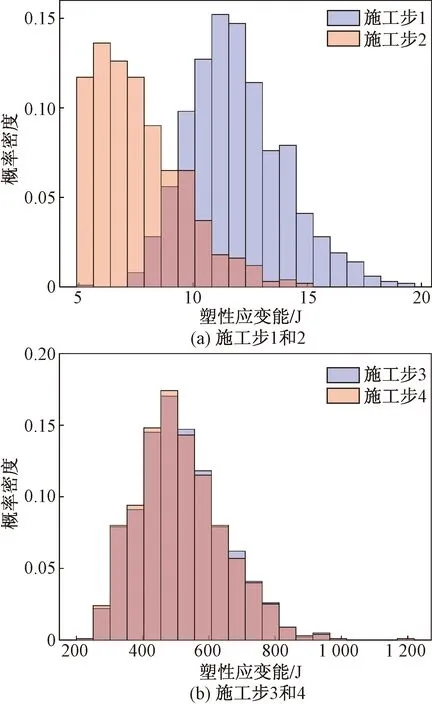
图7 不同施工步下塑性应变能概率密度分布Fig.7 The probability density distribution of plastic strain energy under different construction steps

在进行基坑开挖的随机场-有限差分模型计算的过程中，通过提取每个单元的弹性应变能与塑性应变能进行统计分析，研究基坑开挖过程中的能量演化特征。图7给出了不同施工步下，考虑空间变异性的基坑总塑性应变能的概率密度分布，可以看出，塑性应变能的分布均满足对数正态分布，这也模量随机场所采用的分布相一致。随基坑的开挖，塑性应变能逐渐增大，这说明开挖引起基坑内部更多的土体单元发生了塑性变形，引起能量的耗散。对于图7(b)中施工步3和4的概率密度分布发现，两道钢支撑的拆除几乎没有引起塑性应变能的变化，这表明基坑开挖完成后，基坑内部呈现较好的能量分布情况，即基坑的状态较为稳定。

图8给出了不同施工步下基坑弹性应变能的变化曲线，随施工的进行，基坑的总弹性应变能呈现逐渐降低的趋势，与图7类似，施工步3和4对应的弹性应变能基本一致，再次验证了钢支撑的拆除对基坑的稳定性无影响。根据能量守恒准则，外力对岩土工程系统做的功主要转化为可释放的弹性应变能、塑性应变能、动能、重力势能等，在系统内部，弹性应变能又可以转化为塑性应变能。结合本模型的实际情况研究，弹性应变能随开挖进行逐渐减少，这其中一部分应该转化成了塑性应变能耗散，另外由于本模型考虑了开挖过程，因此在能量计算时，开挖部分的单元不存在能量，这也造成了弹性应变能的大幅减少。

图8 不同施工步下弹性应变能变化曲线Fig.8 Variation curve of elastic strain energy under different construction steps

3 结论

依托佛山市某综合管廊基坑项目，基于随机场理论表征基坑土体参数的空间变异性，建立了复杂多层土的随机场模型，采用FLAC软件建立了基坑开挖的有限差分模型，研究考虑空间变异性的基坑施工过程中变形特征及能量的演化规律，主要结论如下。

(1)构建了复杂多层土的随机场-有限差分耦合计算基坑开挖的数值模型，该模型考虑了不同土层弹性模量的空间变异性，实现了随机场基坑开挖的模拟，为本研究依托的管廊基坑项目提供了一套更为科学的数值计算方法。

(2)考虑空间变异性的基坑施工变形分析表明，基于均质模型与随机场模型的测点变形趋势一致，基于地表测点变形和深部测点变形的计算结果来看，现有的基坑支护措施能够有效保障基坑开挖施工的安全。通过深部测点实测值的对比验证了模型的准确性，随机场模型能更准确地反映实际工程的力学响应。实际的不同测点处变形量的变异性不同，在施工过程中需要重点关注变异性较大的区域。

(3)考虑空间变异性的基坑施工能量演化研究表明，基坑施工完成后，两道钢支撑的拆除对基坑内部的能量分布几乎无影响，开挖完成后基坑处于稳定状态。基坑开挖过程中弹性应变能减少，主要转化为塑性应变能以及由于开挖而消失单元中所存储的能量。