参数可变强非局域非线性介质中球贝塞尔孤立波

梁检初，万 凯，刘 佟，强 娜，李雅洁，徐四六

（1. 惠州学院 电子信息与电气工程学院, 广东 惠州 516007;2. 广东省电子功能材料与器件重点实验室，广东 惠州 516007;3. 湖北科技学院 电子信息工程学院，湖北 咸宁 437199）

1 引言

近来强非局域非线性介质中的孤立波引起了人们极大的兴趣。非局域性能够抑制孤子的调制不稳定性，不仅能够支持基本孤子和涡旋孤子，也能支持多孤子束缚态和偶极孤立波，多极孤子等在一般情况下不稳定的结构。实验上在向列液晶，铅玻璃中对这类孤立波的观察进一步刺激了对非局域孤立波的理论研究。

而在空间孤子的研究中，系统参数大都是常数[1-6]。玻色-爱因斯坦凝聚（BEC）中的物质波的演化通常满足Gross-Pitaevskii 方程(简写为G-P 方程)[7]，也就是BEC 中的三维非线性薛定谔方程。归一化G-P 方程可表为：

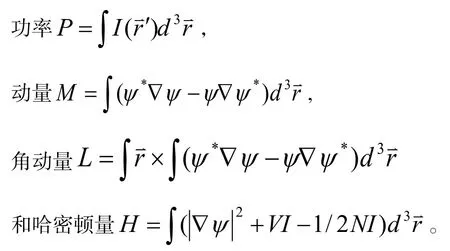
当介质的非线性响应只局限于场点时，响应函数称为δ函数，归一化的非线性项表示为N(I)=I，此即通常所讲的局域三阶效应，方程(1)也成为标准的G-P 方程；在另一相反的极限条件下，响应函数的宽度远远大于光束的宽度，非线性效应为强非局域非线性效应，可以把响应函数在原点处进行泰勒展开，得到因为非线性项中的常数项不影响波的演化，所以非线性项可以写为此时非线性项变成了一个线性项，但该模型仍然描述孤子的非线性现象，事实上，该线性项的系数跟波函数的功率(概率流)相关，也即与物质波波函数相关。钟卫平等得到了该方程的两种解析孤立波解。其一是厄米惠特克孤子解[10]，第二个精确的解析解是库玛-高斯孤立波解[11]。

有关光纤孤子或者说时间孤子的系统中，其动力学机制一般由（1+1）-D 非线性薛定谔方程确定，其色散系数、非线性系数和增益系数等都是可以随光脉冲传播距离变化的，常被称为分布参数系统，或称参数管理系统。事实上在包括非局域非线性介质在内的材料也会类比地存在参数随传播距离变化或随演化时间改变的情况[12-14]。我们[14]首次研究了分布参数的广义二维强非局域非线性介质中的贝塞尔孤立波，并且发现贝塞尔孤波具有不同于高斯孤波、拉盖尔-高斯孤波和Hermite-Gaussian 孤波的独特的属性。作为线性薛定谔方程的本征解，贝塞尔函数有一个重要特点：光场分布函数是贝塞尔函数的光束能够在自由空间中无衍射地传播，也就是说它能以孤子的形式在自由空间传播。因此基于贝塞尔孤子的光子晶格被广泛地应用于离散孤子和带隙孤子的研究，而离散孤子和带隙孤子正是目前的一个研究热点。我们[15]还首次利用雅克比椭圆函数展开法研究了变系数广义三维非线性薛定谔方程，得到了这种常见的非线性发展方程的精确解。这些解的形式是雅克比椭圆函数行波解，其振幅特性和相位特性都给予了相应的分析。除此外分布参数系统中三维空间物质波演化的研究比较少见。

本文中我们通过解析求解的方式获得参数可变系统中(3+1)-D 强非局域非线性G-P 方程的精确解，即球贝塞尔孤立波解。

2 (3+1)-D 变系数强非局域G-P 方程的球贝塞尔孤立波解

我们讨论系数可变的强非局域非线性介质中物质波的自相似演化。可变参数的G-P 方程为：

其中，物质波的衍射系数β，非线性系数Δn，和增益系数g均是随演化时间变化的；强非局域非线性项因为这是在三维空间中，且方程明显有球对称性,我们就在球坐标系中求解方程(3)，球坐标系中拉普拉斯算符是

为寻求方程的自相似解，我们设

式中 Θ(t,r)是待定的自相似变量，w(t)是孤子的特征宽度， 相位取为二次函数(4)式中把径向变量r和角向变量(θ,φ)分离开来。把尝试解(4)代入参数可变系统中三维强非局域G-P 非线性薛定谔方程 (3)，分离实部和虚部，我们得到如下耦合的偏微分方程组：

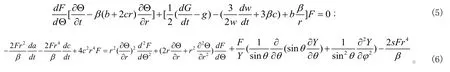
在同一方程中，相同项合并后，各项的系数分别为零，于是以上方程组给出如下一系列关系表达式：

从以上方程中又可以直接得到

所有式子中的下标“0”表示t=0时的初始值,c决定于

由(10)式得

把(18)式代入(17)式得

把这些结果代入方程(6)，我们有方程式

为获得球贝塞尔方程，我们有

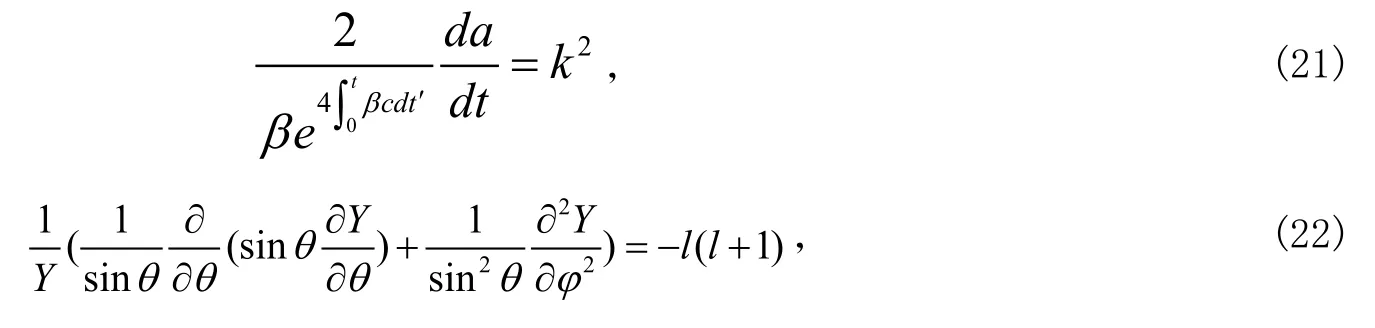
由方程(21)得到

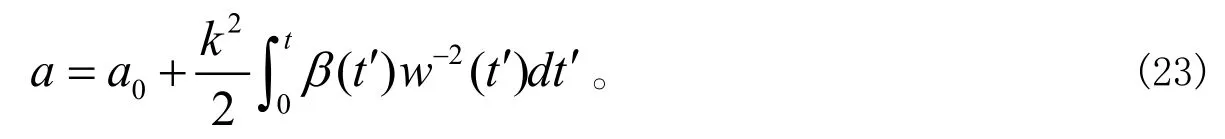
球函数方程(22)的解是球谐函数

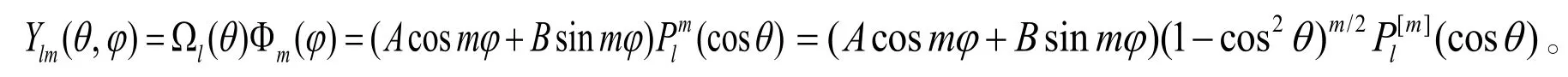
现在方程(20)成为一个球贝塞尔方程：

其解是一个球贝塞尔函数

最后我们得到了方程(3)的三维球贝塞尔自相似孤立波解:

3 球贝塞尔孤立波的特性分析

孤立波解(26)中，特征尺度w由(19)决定，其变化规律类似于二维贝塞尔孤立波的情形[12]。特征变量是半径与特征尺度的比值，表示波函数的形状保持不变，只是尺度大小发生改变，这种性质成为自相似。波函数角向呈球谐函数分布；当系统有增益（g>0）或损耗（g＜0）使，物质波强度（粒子数密度）呈指数增加或减少。该球贝塞尔自相似孤立波的线性相位由(23)确定，空间啁啾系数c由(18)式描述。波的强度即BEC 粒子数密度与自相似特征变量 Θ(r,t) 的关系不随演化时间发生改变，故这是一种广义的孤子，或可称为孤立波。下面讨论不同阶数的自相似球贝塞尔孤立波的特性。

当l=m=0时，(26)式其实表示的是在三维空间球对称分布波函数。其等强度等高图是球形。图1 是l=1和l=2时的孤立波解的强度等高图，即=a(a是常数，且满足0＜a＜1)的曲面图。图1 中的五行分别是l= 1及m=0(第一行)和m=1(第二行)，与l=2及m=0(第三行)，m=1(第四行)和m=2(第五行)的球贝塞尔孤立波的强度等高图。四列分别对应不同观测方向的观测结果（正面，上面，右边和左边）。从图中看出，阶数越高，球贝塞尔孤立波的分布越复杂，呈现多层多极的结构。另外，在高阶球贝塞尔孤立波情况下，波的强度越小的等高图越复杂，但图中没给出。

图1 l=1和 l=2时的贝塞尔孤立波解的强度等高图

再看l=3时的情况。此时其光强分布更复杂，见图2。图中从第一行到第四行分别对应m=0，m=1，m= 2和m=3的情况。m表示了方位角方向的光强调制周期数，俯视图(第二列)被分成(m+1)极。

图2 l=3时的球贝塞尔孤立波解的强度等高图

4 结论

本文研究管理系统强三维非局域非线性Gross-Pitaevskii 方程的精确的孤立波解即球贝塞尔孤立波，探讨了在玻色爱因斯坦凝聚中出现的三维物质波的演化。创新点归结为两点：

本文研究管理系统中空间孤立波(孤子)的研究。过去光通信科研工作者热衷于对管理系统中的光纤孤子即时间孤子的研究，但仅限于时域中的管理系统，少见对空域中管理系统中的孤子或孤立波的研究。然而，现实的用于传播空间孤子的材料都不可能是绝对均匀的。严格来说光束在材料中的衍射系数，非线性系数，增益或损耗系数都会随传播距离变化。并且，为了控制光束的传播，我们也需要人为管理材料的参数。因而管理系统中的空间孤子的研究很有必要。我们在这一方向的创新研究有望刺激相关领域的发展。

本文给出了三维强非局域非线性薛定谔方程的一种新的精确的(3+1)-维孤立波解即自相似球贝塞尔孤立波解，分析了其强度特性及相位特性。