水利风景区PPP项目政府与社会资本方利益协调行为策略研究
2022-07-27吴兆丹王诗琪冯永琴吴文清
吴兆丹,李 彤,王诗琪,冯永琴,吴文清
(1.河海大学商学院,江苏 南京 211100; 2.江苏省水资源与可持续发展研究中心,江苏 南京 210024)
水利风景区,是指以水域(水体)或水利工程为依托,具有一定规模和质量的风景资源与环境条件,可以开展观光、娱乐、休闲、度假或科学、文化、教育活动的区域[1]。在水利风景区中引入政府和社会资本合作(PPP)模式,既有利于缓解政府在景区建设运营中的资金压力,又能满足社会资本方获取经济收益需求,还可以在项目建设运营中充分发挥社会资本方市场化管理功能,提高项目建设运营效率。2005—2022年我国发布了一系列关于水利风景区的通知和管理办法,例如, 2005年的《关于印发水利风景区发展纲要的通知》、2022年的《水利风景区管理办法》。在国家政策的号召下,PPP模式在我国水利风景区项目中的应用初见成效,武汉市金银湖水利风景区水环境建设PPP项目、渭南市少华湖水利风景区PPP项目等进展顺利。
水利风景区PPP项目中,政府和社会资本方基于“利益共享、风险共担、全程合作”原则建立起共同体关系。其中,政府更关注风景区的社会效益和生态环境价值,社会资本方则侧重其经济价值的产出,政府和社会资本方能否达到良性合作对水利风景区PPP项目顺利进行影响较大。由于我国水利风景区中PPP模式应用的起步较晚,目前多数景区PPP项目中政府和社会资本方利益协调机制尚不成熟,仍存在股权、利益、成本、风险等方面分配比例确定不合理问题,从而影响社会资本方参与景区建设运营的积极性,甚至不利于景区的顺利建设运营。因此,有必要对水利风景区PPP项目建设运营中政府和社会资本方的利益协调行为策略展开分析,为有效协调双方利益提供依据。
1 文献综述
国内外已有研究对PPP项目相关主体的利益协调展开了分析。在研究对象上,该类研究主要针对基础设施[2]、交通运输[3-4]、建设工程[5-6]、生态环境[7-8]等领域项目。在研究方法上,PPP项目相关主体利益协调研究多采用演化博弈模型、纳什谈判博弈模型、stackelberg模型等。其中演化博弈模型强调动态均衡,能更准确地反映现实中各博弈主体根据每阶段的博弈及其结果而不断做出调整、处于动态变化过程的情况;该类博弈既不要求参与人是完全理性的,也不要求完全信息条件,从而大大拓宽了应用范围。目前演化博弈模型在经营性PPP项目相关主体利益协调中应用较广,如建筑工程[9-10]、交通运输[11-12]、养老[13]等项目。有关水利工程PPP项目利益主体演化博弈的研究较少,费凯等[14]针对不同政府监管模式构建演化博弈模型,剖析不同情形下政府监管部门与水利工程建设市场主体策略选择的演化路径;丰景春等[15]对农田水利PPP项目运行中,项目公司和农户策略选择进行了演化博弈分析。
可见,目前对PPP项目相关主体利益协调的研究已取得一定进展,但暂无研究针对水利风景区PPP项目进行;已有少数研究针对水利工程PPP项目进行演化博弈分析,其中所涉及利益相关者包括项目公司和农户,或将政府作为监管者,分析其与市场主体之间的博弈过程,而忽视了政府作为PPP项目参与主体,其希望项目顺利进行、获得相应社会、经济、生态、环境效益等动机,以及与之相对应所承担的运行成本、风险等。基于此,本研究针对水利风景区PPP项目政府和社会资本方的利益协调行为策略展开研究,并在演化博弈分析中,同时考虑政府的宏观管理者和项目微观参与主体双重身份,既涉及政府对水利风景区PPP项目的政策支持及保障、经济补贴、监督管理等,又包括政府在项目中的成本支出、收益分配及风险分担等,以期为水利风景区PPP项目建设运营中政府和社会资本双方的利益协调,促进项目顺利建设运营提供参考。
2 模型构建
2.1 模型假设
2.1.1政府与社会资本方的博弈行为
以政府与社会资本方为对象,对水利风景区PPP项目建设运营中的利益协调问题做出如下假设:
a. 政府和社会资本方分别有两种行为选择。政府的行为选择包括“积极”和“不积极”,前者是指政府积极参与项目建设运营,后者是指政府参与项目建设管理的意愿不强烈。 社会资本方行为选择包括“努力”和“投机”。 “努力”是指社会资本方积极参与项目建设运行;“投机”是指社会资本方采取各种方式力求自身获得更多利益。
b. 政府在PPP模式下通过积极与社会资本方合作,能促进项目运行效率提升;而当政府采取“不积极”策略时,社会资本方选择“努力”或“投机”均无法得到经济补贴。社会资本方通过权衡“投机”面临的风险损失和“努力”下的收益,可能会偏向采取投机行为,忽视长期利益。
2.1.2博弈的策略组合
a. 策略组合1:“积极、努力”。此时,政府和社会资本方可以分别得到经济收益S1和S2,并获得额外收益e,包括政府可获得的社会生态效益D和社会资本方可获得的附加效益F。其中政府获得的社会效益主要体现在带动直接就业和间接就业上。社会资本方所获得的附加收益F包括所获得的政府奖励,以及通过合作扩大了总资产的规模,实现了品牌效应和社会影响力的增强。此外,政府所承担项目建设运行成本C1,包括初始投入T1和经营支出E1,另外政府实施“可行性缺口补贴”政策所付出的成本为M;社会资本方所承担项目建设运行成本为C2,包括初始投入T2和经营支出E2。因此,“积极、努力”策略下的政府净收益为S1-C1+D-M,社会资本方净收益为S2-C2+F+M。
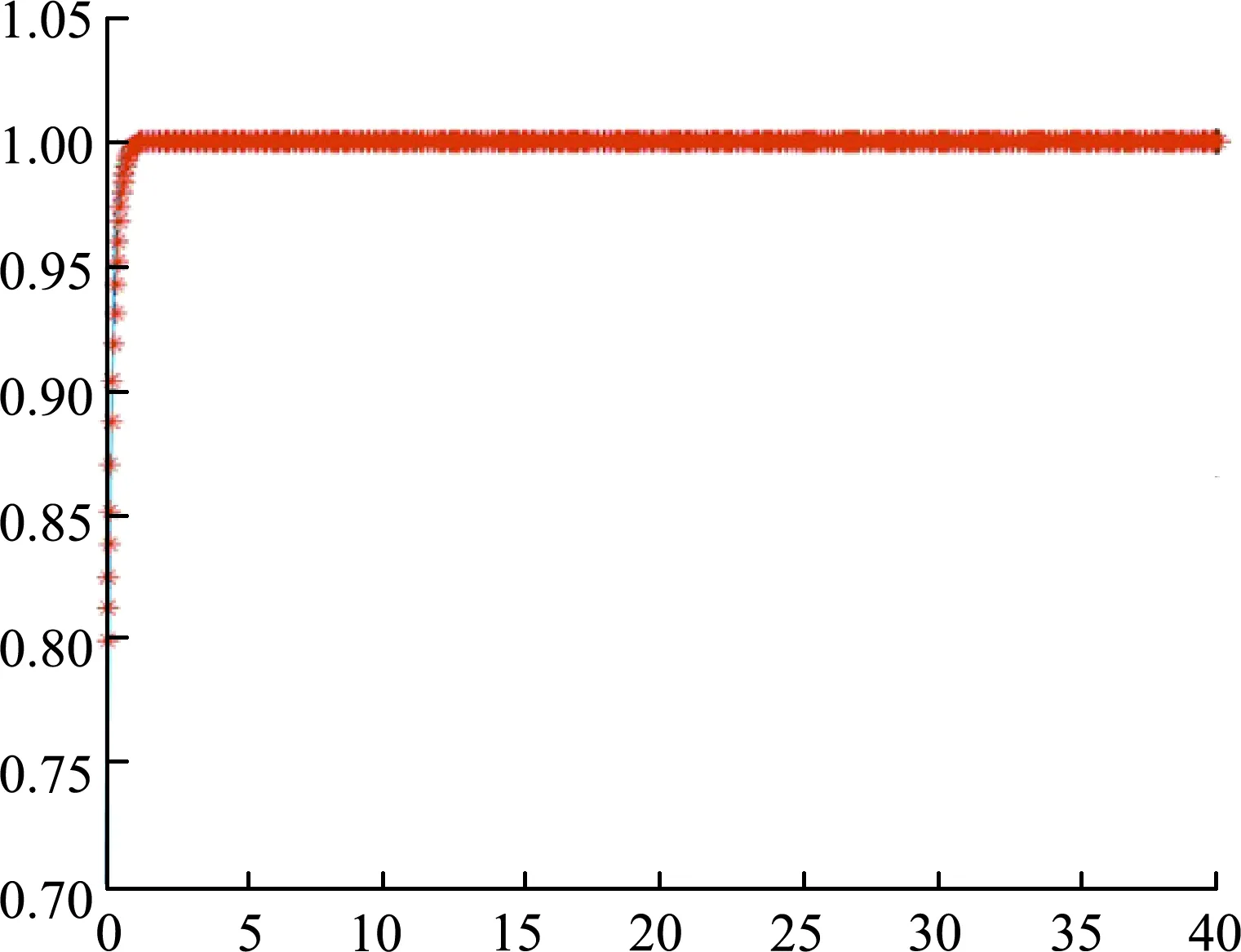
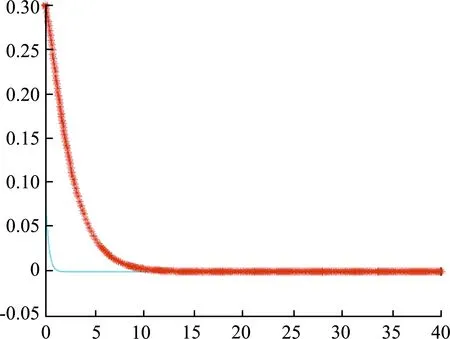
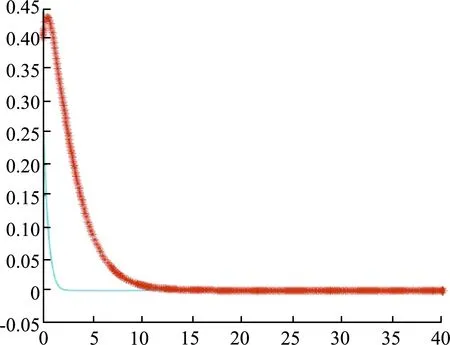
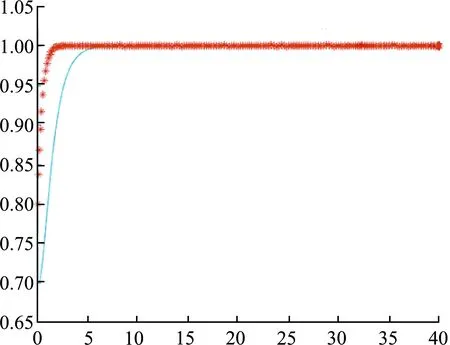
b. 策略组合2:“不积极、努力”。政府采取“不积极”措施所得到的收益为S0,且S0 c. 策略组合3:“积极、投机”。社会资本方采取“投机”行为时,将原本用于项目运作过程中的财力、人力等投向其他经营领域,以获得额外的投机收益b,并丧失了“努力”策略下的影响力和品牌效应,从而没有附加收益F。“积极、投机”策略下项目存在风险成本H0,对应政府净收益为S1-C1+D-M-λH0,社会资本方净收益为S2-(1-λ)H0+b+M。 d. 策略组合4:“不积极、投机”。此时政府损失了项目原本可得的社会生态效益D;社会资本方损失附加效益F,并将资源等投向其他领域获得收益;项目伴有风险成本H。因此该策略下政府净收益为S0-λH,社会资本方净收益为S2-(1-λ)H+b。 结合4种策略组合,构建政府和社会资本方支付矩阵如表1所示。 由于社会资本方付出的项目建设运行成本C2往往大于获得的附加收益F,而转投向其他经营领域的收益b多为正值,因此S2-(1-λ)H0+b+M>S2-C2-(1-λ)H0+F。对于政府方,其所付出的项目建设运行成本C1与可行性缺口补贴成本M之和一般大于所获得的社会生态效益D,且S0小于S1,因此S0-λH0>S1-C1+D-M-λH0。由此可得: S2-(1-λ)H0+b+M>S2- (1) S0-λH0>S1-C1+D-M-λH0 (2) 式(1)、式(2)在λ∈[0,1],b>0,F>0,M>0,H0∈(0,∞)的条件下恒成立,故“不积极、投机”为纳什均衡,“积极、投机”和“不积极、努力”不是均衡策略。 “积极、努力”是否为均衡策略则取决于政府和社会资本方双方在不同策略下的净收益大小关系。这里将根据双方分别在“不积极”或“投机”策略下承担的风险成本与其在“积极”或“努力”策略下付出的项目建设运行成本之间不同的大小关系,假设4种情境,讨论各情境下的静态博弈过程。 a. 情境1:政府采取“不积极”策略所应承担的风险成本λH大于“积极”策略下付出的项目建设运行成本C1,社会资本方采取“投机”策略所应担的风险成本(1-λ)H大于“努力”策略下付出的项目建设运行成本C2。对于“积极、努力”的策略选择,分析如下不等式: S2-C2+F+M>S2-(1-λ)H+b (3) S1-C1+D-M>S0-λH (4) 在式(3)中,根据情境1的假设可得(1 -λ)H>C2,同时由于社会资本方转投向其他经营领域的收益b,往往小于社会资本方获得的附加收益F与政府提供的可行性缺口补贴M之和,即F+M>b,因此S2-C2+F+M>S2-(1-λ)H+b恒成立。在式(4)中,由于政府得到的社会生态效益D具有持续性,往往大于所需付出的“可行性缺口补贴”M,同时根据情境一的假设,得λH>C1,故S1-C1+D-M>S0-λH也成立。因此,式(3)(4)均成立,“积极、努力”策略达到纳什均衡。 b. 情境2:政府采取“不积极”策略所应承担的风险成本λH小于“积极”策略下付出的项目建设运行成本C1,社会资本方采取“投机”策略所应担的风险成本(1-λ)H小于“努力”策略下付出的项目建设运行成本C2。于是可得(1-λ)H c. 情境3:政府采取“不积极”策略所应承担的风险成本λH大于“积极”策略下付出的项目建设运行成本C1,社会资本方采取“投机”策略所应担的风险成本(1-λ)H小于“努力”策略下付出的项目建设运行成本C2。在该假设下分析政府和社会资本方双方的净收益关系,由于S1>S0、-C1>-λH、D-M>0,故S1-C1+D-M>S0-λH。而S2-C2+F+M和S2-(1-λ)H+b的大小关系与情境2中相同,因此当社会资本方获得的附加效益和可行性缺口补贴之和远大于转投向其他经营领域的收益时,“积极、努力”策略达到纳什均衡。 表1 水利风景区PPP项目政府与社会资本方静态博弈的支付矩阵 d. 情境4:政府采取“不积极”策略所应承担的风险成本λH小于“积极”策略下付出的项目建设运行成本C1,社会资本方采取“投机”策略所应担的风险成本(1-λ)H大于“努力”策略下付出的项目建设运行成本C2。此时F+M>b、-C2>-(1-λ)H,得到S2-C2+F+M>S2-(1-λ)H+b。同情景2,S1-C1+D-M和S0-λH的大小关系依情况而定,当-C1+D-M>-λH,即政府所得的社会生态效益远大于可行性缺口补贴成本时,“积极、努力”策略能够达到纳什均衡。 上述静态博弈分析得出了不同情境下对应的纳什均衡点。而现实中,政府和社会资本方会通过衡量每阶段的博弈及其结果不断调整行为策略。这里将针对上述4种情境,分析水利风景区PPP项目中政府和社会资本方行为策略选择的动态演化过程。 假设政府选择“积极”的概率为x(0≤x≤1),选择“不积极”的概率为1-x;社会资本方选择“积极”的概率为y(0≤y≤1),选择“投机”的概率为1-y。则社会资本方选择“努力”策略下的期望收益UP、“投机”策略下的期望收益UNP分别为 UP=x(S2-C2+F+M)+(1-x)[S2- (5) UNP=x[S2-(1-λ)H0+b+M]+ (6) 社会资本方平均期望收益UA为 UA=yUP+(1-y)UNP (7) 政府选择“积极”策略下的期望收益UQ和“不积极”策略下的期望收益UNQ分别为 UQ=y(S1-C1+D-M)+ (8) UNQ=y(S0-λH0)+(1-y)(S0-λH) (9) 政府平均期望收益UB可表示为 UB=xUQ+(1-x)UNQ (10) 则复制动态方程为 (11) x(1-x)[λ(2H0-H)y+S1-C1+ (12) 令G(x)=0,F(x)=0,得到该动态演化博弈系统的局部驻点,分别为M1(0,0),M2(0,1),M3(1,0),M4(1,1),M5(x0,y0) 。求解得: 构建雅可比矩阵: (13) 雅可比矩阵各驻点参数值见表 2,其中, (14) (15) 表2 雅可比矩阵各驻点参数值及各情境下稳定性 a. 情境1下各驻点的稳定性见表3。在政府采取不积极策略所付出的风险成本大于积极的项目建设运行成本,社会资本方采取投机策略的风险成本大于努力的项目建设运行成本的情况下,根据M1(0,0),有detJ>0,trJ<0,因此该点为演化稳定点。对于M2(0,1),有detJ>0,trJ>0,该点为不稳定点。对于M3(1,0),有detJ>0,trJ>0,该点为不稳定点。对于M4(1,1),有detJ>0,trJ<0,该点为演化稳定点。对于M5(x0,y0),有detJ<0,trJ=0,该点为鞍点。于是得到对应系统均衡点M1和M4,即“不积极、投机”策略和“积极、努力”策略。 b. 情境2下各驻点的稳定性见表2。在政府采取不积极策略所付出的风险成本小于积极的项目建设运行成本,社会资本方采取投机策略的风险成本大于努力的项目建设运行成本的情况下,对于M1(0,0),有detJ>0,trJ<0,因此该点为演化稳定点。对于M2(0,1),有detJ<0,trJ符号不确定,该点为鞍点。对于M3(1,0),有detJ<0,trJ符号不确定,该为鞍点。对于M4(1,1),有detJ>0,trJ>0,该点为不稳定点。对于M5(x0,y0),有detJ<0,trJ=0,该点为鞍点。故得到对应系统均衡点M1,即“不积极、投机”策略。 c. 在情境3中分析各驻点的稳定性,可得到支付矩阵中的S2-C2+F+M和S2-(1-λ)H+b、公式S1-C1+D-M和S0-λH的大小关系不能确定,各驻点是否为稳定点以及相对应的系统均衡点,需根据实际情况进行分析判定。情境4与之类似,系统均衡点需代入实际数值来确定。 采用Matlab软件,利用ode45命令对动态演化博弈模型进行模拟仿真,分析上述存在均衡策略的情境1和情境2下主体间博弈过程。 a. 情境1。根据上述该情景所设置变量大小关系,假设M=2,H=15,λ=0.6,F=6,C2=5,D=1.5,C1=3,b=1,S1=10,S0=7,H0=15,假定(x,y)的最初值分别为(0.1, 0.3)、(0.3, 0.4)、(0.6, 0.8)、(0.7, 0.8),仿真分析结果如图1所示。 可以看到,当政府采取“不积极”策略,社会资本方采取“投机”策略所要付出的风险成本大于双方选择“积极”或“努力”所付出的项目建设运行成本时,政府以及社会资本方更倾向于选择都积极努力。当(x,y)=(0.1, 0.3),(x,y)=(0.3, 0.4),(x,y)=(0.6, 0.8),(x,y)=(0.7, 0.8)时,可以看到x,y的演化趋势都收敛于1,表明政府和社会资本方无论有多大合作概率,政府都倾向于采取“积极”策略,社会资本方都倾向于采取“努力”策略,最终都会演化至选择积极合作。 b. 情境2。根据上述该情景所设置条件,假设M=2,H=10,λ=0.4,F=2,C2=7,D=1.5,C1=5,b=1,S1=10,S0=7,H0=10。仿真结果如图2所示。 (a)(x,y)=(0.1, 0.3) (b)(x,y)=(0.3, 0.4) (c)(x,y)=(0.6, 0.8) (d)(x,y)=(0.7, 0.8) (a)(x,y)=(0.1, 0.3) (b)(x,y)=(0.3, 0.4) (c)(x,y)=(0.6, 0.8) (d)(x,y)=(0.7, 0.8) 可以看到,当(x,y)=(0.6, 0.8)和(x,y)=(0.7, 0.8)时,x、y的演化趋势都收敛于1。即当政府采取“不积极”策略,社会资本方采取“投机”策略时所要付出的风险成本小于选择“积极”或“努力”所付出的项目建设运行成本时,双方的合作意愿都较大;当(x,y)=(0.1, 0.3)和(x,y)=(0.3, 0.4)时,可以看到x的演化趋势都趋于1,y的演化趋势都收敛于0,表明了如果两者积极合作获得的总收益小于积极合作时所付出的总成本时,且积极合作的概率较小,政府和社会资本方都会选择不合作。 a. 当政府采取“不积极”策略、社会资本方采取“投机”策略所承担的风险成本分别大于其“积极”“努力”策略下付出的项目建设运行成本时,“积极、努力”策略在静态博弈、动态博弈中均达到均衡。 b. 只有满足政府获得的社会生态效益远大于支出的可行性缺口补贴,且社会资本方获得的附加收益和可行性缺口补贴之和远多于转投向其他经营领域所获得的收益,“积极、努力”策略才会成为静态及动态均衡结果。 a. 完善收益分配、风险分担及政策保障机制。一方面,建立合理的收益分配和风险分担机制,明确划分政府和社会资本方的相关权利和责任。根据本文分析结果,应尽量满足政府采取“不积极”策略所应担的风险成本大于“积极”策略下付出的项目建设运行成本、社会资本方采取“投机”策略所应担的风险成本大于“努力”策略下付出的项目建设运行成本,以确保“积极、努力”是均衡策略,促进双方积极合作以及项目正常运营;另一方面,建立健全政府保障机制,包括提供制度支撑、兜底政策、资源配置等,考虑设计允许特许经营期延长、协议内容动态调整、政府保障不能实现的后备条款等,促进社会资本参与并确保项目长期良好运营。 b. 建立政府和社会资本方沟通机制。政府和社会资本方双方或其中一方采取消极策略产生的共担风险成本是PPP项目成本的重要组成部分,而有效的沟通机制有利于降低该成本,促进项目建设运营的顺利进行。基于此,本文建议借助电话、“互联网+政务服务”平台等,构建水利风景区PPP项目多元化的沟通渠道,提高沟通效率;构建常态化座谈会等定期沟通机制,提高双方合作效率。 c. 加强对水利风景区PPP项目的监管力度。社区监管与政府监管并行,公开监管情况,有利于降低社会资本方采取“投机”策略的可能性,保障项目顺利运营。可出台操作性较强的地方性政策规定,规范水利风景区PPP项目的建设与运营流程;考虑建立垂直监管机制,让项目管理机构接受省级或中央水利风景区管理部门垂直领导,提高管理效力;建立健全社区监管机制,完善举报受理的渠道,设立专门的网络留言平台及电话热线,及时受理和解决群众反映的问题,让群众参与到监管中去。2.2 静态博弈
C2-(1-λ)H0+F
2.3 动态演化博弈
C2-(1-λ)H0+F]
(1-x)[S2-(1-λ)H+b]
(1-y)(S1-C1+D-M-λH0)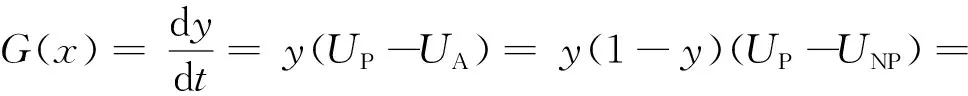
D-M-S0+λ(H-H0)]2.4 系统稳定性研究

3 仿真分析

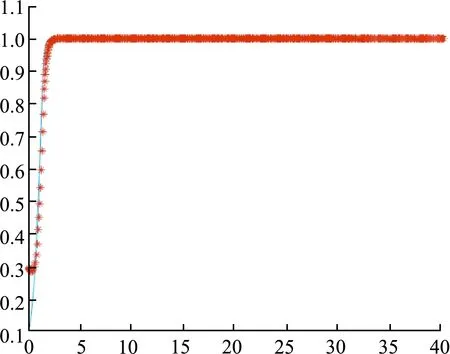
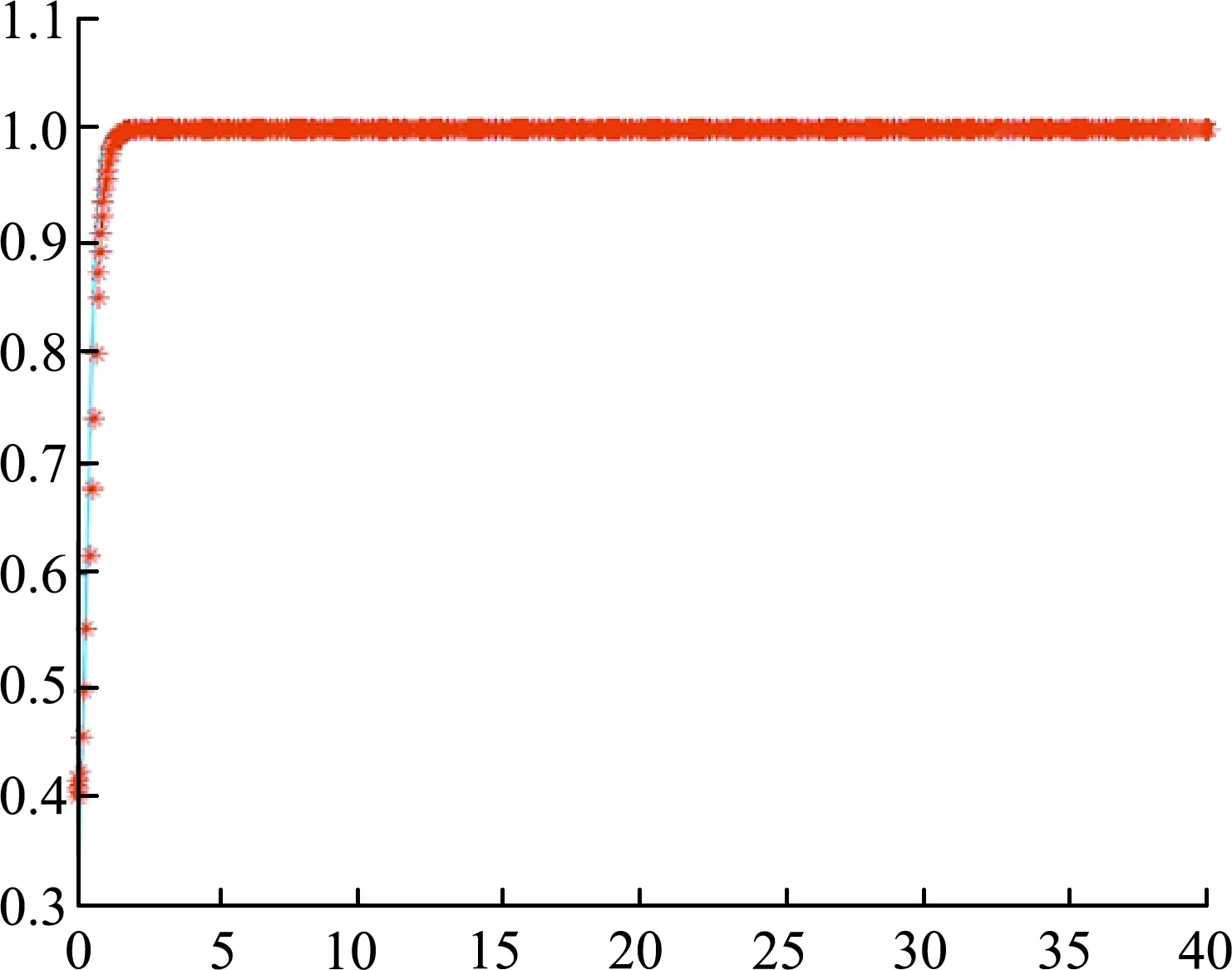
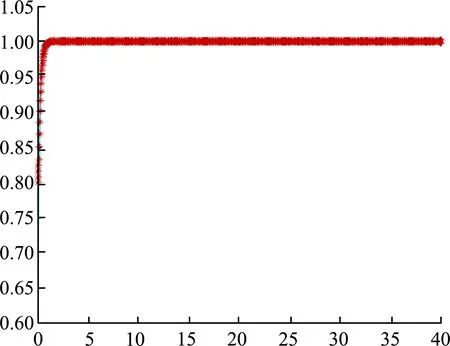

4 结论与建议
4.1 结论
4.2 建议
