基于模糊偏好的冲突决策共识模型研究
2022-07-27张瑾木子徐海燕
张瑾木子,徐海燕,陈 璐
(南京航空航天大学经济与管理学院,江苏 南京 211106)
冲突是由决策各方利益差异引发的一种对立现象,普遍存在于水资源冲突、能源冲突以及大气污染争端等领域。如何正确分析并解决现实冲突,对我国经济、能源和环境的高质量均衡发展具有重要意义。目前,学者们已基于经典博弈论对冲突问题进行了大量研究,但该理论以大量精确数据为基础,很难应用到实际冲突问题的解决中。
冲突分析图模型(graph model of conflict resolution, GMCR)[1]是在博弈论和偏对策理论的基础上发展起来的,决策过程中只需相对偏好信息,就能为决策者提供科学有效的冲突解决方案。针对冲突分析图模型中逻辑表达复杂、计算烦琐的问题,Xu等[2-6]提出了图模型矩阵理论,极大地推动了图模型理论的发展和决策支持系统的开发。
如何对冲突问题运用最合适的偏好是建模至关重要的一步,直接影响到图模型的优劣程度。早期冲突分析图模型仅考虑简单偏好的情况。简单偏好是一种相对确定的偏好,以信息的完备与确定为前提,简单偏好结构包括优于(“≻”)和等价于(“~”)两种表现形式。但由于客观世界的复杂性、决策者所处环境的不确定性,决策者无法把握两个状态之间的确定偏好。Li等[7]在简单偏好的基础上,引入了不完全信息“U”,构建了一个新的不完全偏好结构{≻,~,U}。Ben-Haim等[8]为描述偏好的不完全性,也建立了一个信息缺失模型。考虑决策者决策模糊性的本质,Al-Mutairi等[9-10]基于模糊集理论,提出模糊偏好的概念。Bashar等[11-13]进而提出了模糊偏好下的冲突分析图模型理论,随后又提出了基于区间模糊偏好关系的冲突分析图模型。在模糊偏好的基础上,Wu等[14]构建了图模型下稳定性的矩阵表达。
以上研究大多将决策者的偏好独立看待,忽略了偏好之间的相互关系,Inohara等[15-16]将决策者的态度划分为积极、中立和消极3个方面,构建了基于决策者态度的冲突分析图模型系统框架。Walker等[17]和Xu等[18]引入了决策者态度因素,研究了决策者积极、中立、消极3种态度对偏好信息的影响,但没有对决策者不同态度下的稳定性进行改进。赵士南等[19]将决策者的偏好划分为共识与非共识偏好,对冲突决策共识模型进行了研究,但其仅仅考虑了简单偏好下决策者偏好和稳定性的变化,没有考虑决策者主观判断的模糊性特点,因而在处理冲突共识问题时降低了模型的普适性。
在现实冲突中,决策环境是复杂的,决策者是有限理性的,当考虑与其他决策者的共识偏好时,其偏好信息也存在一定的模糊性。模糊性是众多冲突决策问题的共性特征,如何在模糊信息下实现决策者共识一直是冲突决策领域关注的热点。因此,本文将模糊理论中的梯形模糊数引入决策者的偏好设置中,对偏好信息进一步划分,建立了基于模糊共识偏好和模糊非共识偏好的冲突决策模型。同时,基于现有三角模糊数和梯形模糊数的清晰化方法,提出了改良梯形模糊数去模糊化法,并应用于模糊偏好关系的处理,构建了决策者在模糊共识和非共识下偏好和稳定性的逻辑表达式。为了简化稳定性的计算,促进决策支持系统的开发,构建了对应的矩阵表达式,并运用到湄公河流域水资源冲突事件中,验证了理论的有效性。
1 理论基础
1.1 冲突分析图模型理论
冲突分析图模型可以表示为V={N,S,P,G}。其中,N表示冲突中所有决策者组成的有限非空集合;S表示所有可行状态的非空集合;P表示决策者的偏好信息;G={S,Ai}表示状态转移图,其中有向弧集Ai⊆S×S表示决策者i从弧的起始状态经过一步转移可以到达弧的终点状态。
1.1.1偏好结构
在冲突分析图模型理论中,对于决策者i∈N,状态s,q∈S,各状态点的偏好结构可以表示为Pi={≻i,~i}。其中,s≻iq表示对于决策者i,状态s优于状态q;s~iq表示对于决策者i,状态s和状态q是等价的。相应地,siq表示对于决策者i,状态s优于或等价于状态q。
1.1.2可达集
定义1可达集。如果决策者i从初始状态s开始可达到的状态集合可以表示为Ri(s)={q∈S:(s,q)∈Ai},则称集合Ri(s)为决策者i从初始状态s出发的可达集。

1.2 冲突分析图模型矩阵表示
冲突分析图模型矩阵表达中,E表示元素均为1的m×m阶矩阵。设矩阵A=(A(s,q))m×m,B=(B(s,q))m×m,则W=A○B=(A(s,q)·B(s,q))m×m。其中:A(s,q)和B(s,q)分别表示矩阵A和矩阵B中位于第s行q列的元素,“○”表示矩阵的Hadamard乘积。对于矩阵A,sign(A)的元素为

(1)
定义3可达矩阵。对于决策者i∈N,状态s,q∈S,如果矩阵Ji=(Ji(s,q))m×m满足
(2)
则称Ji为决策者i的可达矩阵。
1.3 模糊偏好关系理论
Zadeh[20]提出的模糊集理论是处理决策问题中不确定特征、构建决策者不确定偏好的有效工具。Orlovsky[21]基于模糊概念,将清晰偏好关系扩展为模糊偏好关系。




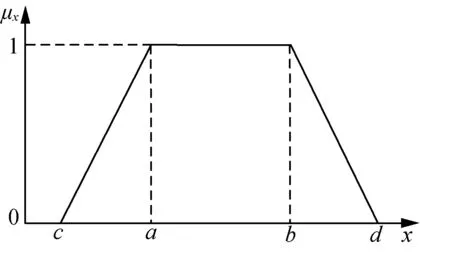
图1 梯形模糊数的隶属度函数
2 基于模糊偏好的冲突决策共识与非共识模型构建
2.1 基于模糊偏好的冲突决策共识与非共识模型逻辑表达构建
2.1.1改良模糊偏好关系
Wu等[14]在Orlovsky[21]模糊偏好关系的基础上对模糊偏好程度及模糊偏好值进行了具体解释。但在实际计算中,存在部分模糊程度区间无法解释的情况,因此,本文对其进行如下改良。

pi,sq=(csq,asq,bsq,dsq)
pi,qs=(1-dsq,1-bsq,1-asq,1-csq)
pi,ss=(λi,λi,λi,λi)
其中,λi(0.5<λ≤1)为决策者i的模糊满意阈值,当且仅当清晰值xi,crisp(s,q)>λi时,决策者i从当前状态s单边转移到状态q。

步骤1标准化:
(3)
Δmax,min=ds,max-cs,min
(4)
(5)
(6)
(7)
(8)
步骤2计算标准值的左右边界:
(9)
(10)
步骤3计算标准化清晰值:
(11)
步骤4计算最终清晰值:
xsq,cp=cs,min+xsq,ncp·Δmax,min
(12)
对于决策者i∈N,梯形模糊数的清晰化偏好值xi,sq,cp=xi,cp(s,q)具体解释如下:①当xi,sq,cp=1时,状态s完全优于状态q,即s≻iq;②当λi
2.1.2模糊共识与非共识改良可达集
模糊共识改良集是指所有决策者收益均得到模糊改良的状态集,模糊非共识改良集是指仅有决策者自身收益得到模糊改良的状态集。



模糊共识改良可达集是指决策者i从初始状态s出发,经过一步转移可以到达的,使所有决策者收益均得到模糊改良的可达状态的集合。


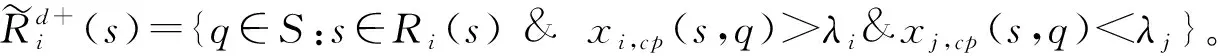

2.1.3模糊共识偏好下稳定性逻辑表达构建
稳定性分析是冲突分析图模型的核心内容,即通过求取决策者个体稳定解得到使所有决策者都满意的均衡解,用于判断决策者在当前状态下是否有改进的动机。目前冲突分析图模型稳定性包括5种:纳什稳定(Nash)[23-24]、一般超理性稳定(GMR)[25]、对称超理性稳定(SMR)[25]、序列稳定(SEQ)[26]、和对称序列稳定(SSEQ)[27]。
如果决策者希望冲突群体实现共赢,则会优先选择与群体达成模糊共识偏好。本文将定义模糊共识偏好下决策者的逻辑稳定性FCGS,其中GS代表图模型5种稳定性中的某一个。
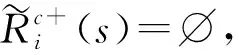
当决策者i选择与冲突群体达成的模糊共识改良集时,所有决策者均能实现共赢,所以冲突对手不可能对其进行非理性反击,因此现实中不存在FCGMR和FCSMR情况。当对手在利己情况下对决策者i进行反击时,FCGMR和FCSMR分别退化为FCSEQ和FCSSEQ。

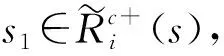
2.1.4模糊非共识偏好下稳定性逻辑表达构建
如果决策者只追求自身利益,则会优先选择模糊非共识偏好。本文将定义模糊非共识偏好下决策者的逻辑稳定性FDGS。
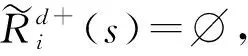




2.2 基于模糊偏好的冲突决策共识与非共识模型矩阵表达构建
2.2.1模糊共识与非共识改良可达矩阵
定义20模糊改良偏好矩阵。令决策者i∈N,状态sk,sh∈S,则决策者i的模糊改良偏好矩阵为
(13)
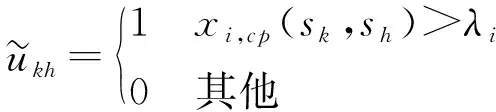

定义21模糊共识与非共识偏好矩阵。令决策者i,j∈N,状态sk,sh∈S,则决策者i和j的模糊共识与非共识偏好矩阵为
(14)
其中
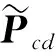
定义22模糊共识改良矩阵。令决策者i,j∈N,状态sk,sh∈S,则决策者i的模糊共识改良矩阵为
(15)
其中
定义23模糊非共识改良矩阵。令决策者i,j∈N,状态sk,sh∈S,则决策者i的模糊非共识改良矩阵为
(16)
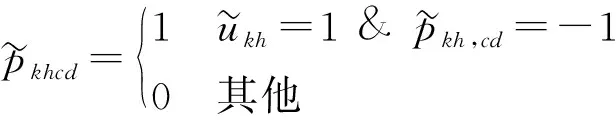
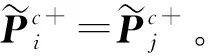
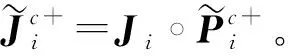
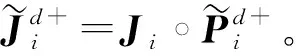
2.2.2模糊共识偏好下稳定性矩阵表达构建
为便于稳定性的计算,促进决策支持系统的开发,本节基于已构建的稳定性逻辑表达与基础矩阵,给出模糊共识偏好下稳定性矩阵表达定义。



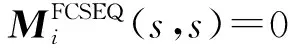





2.2.3模糊非共识偏好下稳定性矩阵表达构建






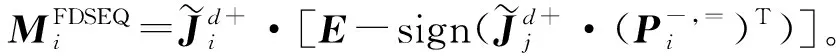
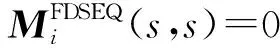


3 案例分析:湄公河流域水资源冲突
3.1 案例背景描述
湄公河是东南亚第一大河,自北向南流经中国、缅甸、老挝、泰国、柬埔寨、越南。该流域水量丰沛、季节性变化明显,适宜整体开发。但流域内各国的水资源需求、经济状况、政治背景、宗教信仰等差异显著,使得开发利用方式变得困难重重。中国位于湄公河上游,十多年来,中国累计在干流修建了11座大坝。关于中国在湄公河下游修建梯级水电站大坝的潜在影响一直存在争论。自发生极端的下游洪水或干旱事件后,外界开始猜测中国大坝的影响,流域内各国冲突问题愈发尖锐。
3.2 决策者及其策略
湄公河流域水资源冲突主要涉及中国、缅甸、老挝、泰国、柬埔寨、越南六国,其中老挝、泰国、柬埔寨和越南被纳入湄公河流域委员会。缅甸因仅有极少部分国土位于流域内,且经济水平较低、实力有限,长期不参与湄公河事务。因此,冲突决策者可以归结为:中国(DM 1)和湄委会(DM 2)。
中国地处上游、地势优越,实施水利项目是其经济发展的必然要求。因此,中国可能选择保持现状,继续建坝发电。然而,迫于国际舆论压力,中国也可能选择与下游国家谈判,共享水文信息和技术以缓解冲突。
湄委会鉴于下游异常灾害的发生,可能选择继续质疑中国建坝发电的影响。但考虑中国国际地位不断提升,湄委会希望与中国保持长期对话伙伴关系,因此,可能会选择与中国协商合作,以加强国家间的发展和联系(表1)。

表1 湄公河流域水资源冲突决策者及其策略
3.3 可行状态及状态转移图
在湄公河流域水资源冲突中,共有2个决策者、4种策略,理论上共产生24=16种状态。考虑部分策略不可能同时发生,剔除不可行状态后,剩余5种可行状态,如表2所示。其中,符号“Y”和“N”表示对应策略被选择和不被选择。例如状态s1表示决策者DM 1选择继续建坝发电,DM 2选择继续质疑DMI。状态s5表示当决策者DM 1选择停止建坝时,流域内各国间冲突自动消解。
图2包含了两个决策者的状态转移,其中圆圈代表冲突可行状态,有向弧的箭头方向表示由初始状态转移到可行状态。

表2 湄公河流域水资源冲突可行状态

图2 湄公河流域水资源冲突可行状态转移图
根据状态转移图,得到DM 1和DM 2的可达矩阵J1和J2。
3.4 决策者偏好信息
在湄公河流域水资源冲突中,中国和湄委会分别从自身角度给出策略选择声明,如表3所示。
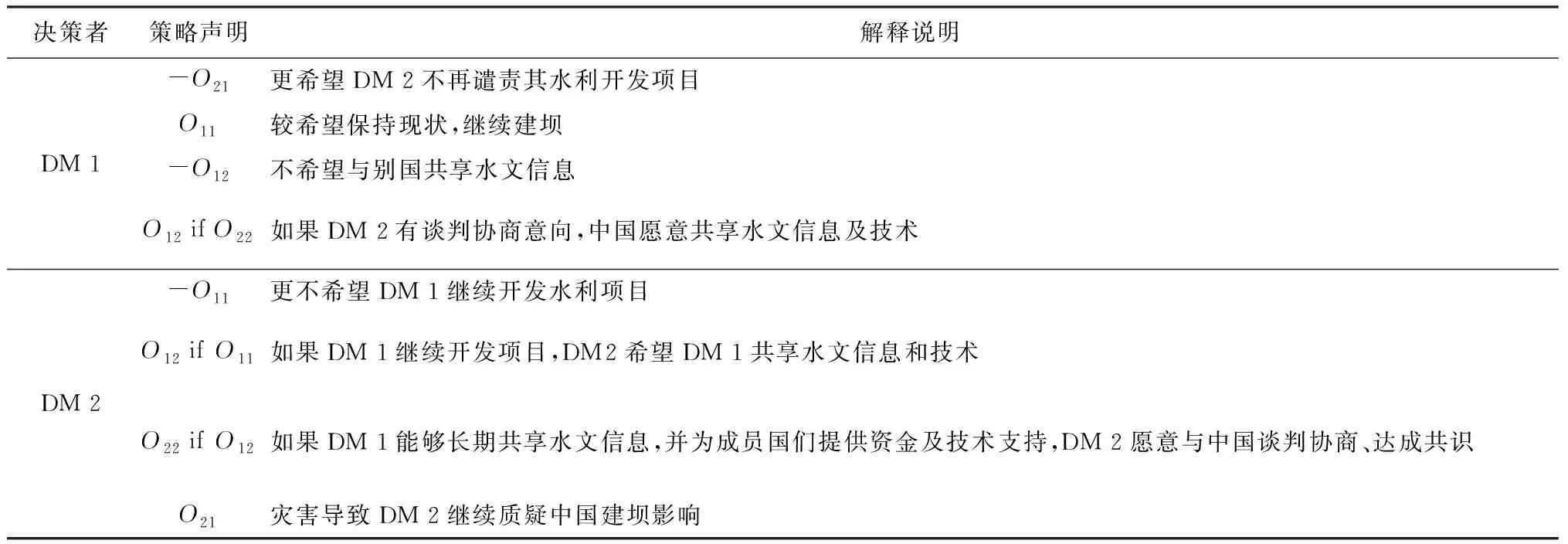
表3 湄公河流域水资源冲突中决策者的策略声明及解释
基于决策者对可行状态偏好的模糊程度,构建状态间语言偏好度表,如表4所示。

表4 状态间的语言偏好度
根据表3和表4,结合公式(3)-(12),计算清晰值偏好矩阵P1,crisp和P2,crisp。
由定义19,当λ1=0.7,λ2=0.6时,DM 1和DM 2的模糊改良偏好矩阵分别为
由定义20,共识与非公式偏好矩阵为
3.5 共识偏好下的稳定性分析
如果中国和湄委会均采取共赢策略,则两者更加关注彼此的共识偏好。根据第2节给出的稳定性定义,计算得到该冲突在模糊共识偏好下的稳定性结果,如表5所示。其中:“Eq”表示某状态对于所有决策者是均衡解;“√”表示在某个稳定性定义下某状态对某决策者是稳定的;“*”表示在任何稳定性定义下都均衡的最优解。
由表5可知,如果决策双方都考虑群体共同利益,则冲突均衡解为s2、s4和s5。其中,s2表示中国选择继续建坝发电,湄委会选择与中国协商谈判;s4表示中国不仅保持现状,还与湄委会分享水文信息和技术,支持成员国开发水利项目;s5表示中国选择不继续开发项目,冲突自动消解。
3.6 非共识偏好下的稳定性分析
如果中国和湄委会均为利己型决策者,则两者更注重自身利益。根据第2节给出的稳定性定义,计算得到该冲突模糊非共识偏好下的稳定性结果,如表6所示。
由表6可知,如果中国和湄委会都采取利己策略,则模糊共识偏好下的博弈均衡解s2和s4消失,只存在冲突的强均衡解s5。即当决策双方都坚持自身利益时,只有中国选择不继续开发水利项目,冲突才能结束。
综上可知,模糊共识偏好和模糊非共识偏好下冲突稳定性更加丰富多样,不仅考虑了决策者主观判断模糊性的特点,也充分刻画了决策过程中存在的共赢和利己行为方式,更加符合现实情况,能够更为准确地为决策者提供冲突解决方案。
4 结 论
本文考虑决策者主观判断的模糊性特点,提出了改良梯形模糊数去模糊化法,并应用于决策者偏好设置中,构建了决策者在模糊共识和非共识下偏好和稳定性的逻辑表达及对应矩阵表达,简化了计算过程、便于求解算法的开发。将构建的模型应用于湄公河流域水资源冲突。通过提取实际案例中涉及的决策信息,求取冲突均衡解,为决策者提供最优解决方案和决策支持。
本文提出的模糊偏好下的冲突决策共识模型考虑的是两个决策者的情况,未来不仅可以进一步扩大至模糊偏好下多个决策者的冲突决策共识研究,还可以考虑其他不确定性下(如灰色、粗糙集等)共识偏好或稳定性的变化情况,增强理论的普适应和推广价值。

表5 模糊共识偏好下的冲突共识稳定性分析结果
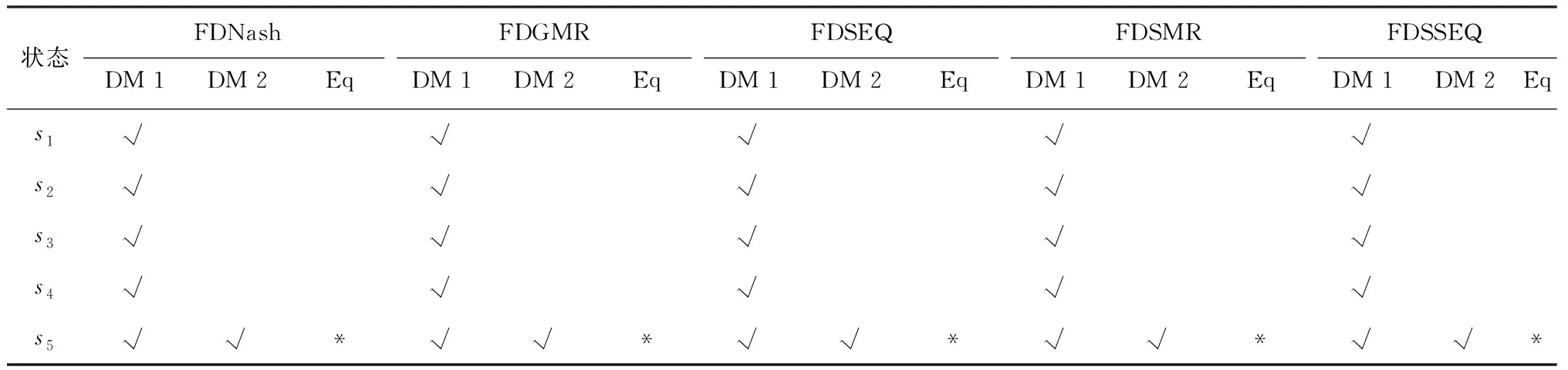
表6 模糊非共识偏好下的冲突稳定性分析结果
