开孔冷弯薄壁槽钢柱偏载稳定性能研究
2022-07-27姚永红黄金炳
姚永红,黄金炳
(安徽理工大学 土木建筑学院,安徽 淮南 232001)
冷弯型钢作为一种高效节能的轻型薄壁钢材,与热轧型钢相比具有壁厚均匀、截面形状多样以及回转半径和惯性矩大等优良的力学性能,常被制作成门式刚架、墙梁、墙柱等构件,在建筑结构中广泛应用。冷弯型钢因壁厚较薄,截面形式大多是非闭合的,在受力时易发生失稳,因此稳定问题是影响冷弯薄壁型钢构件承载力的关键因素[1]。为提高构件承载力,常在冷弯薄壁型钢截面上设置加劲肋,研究表明,此举可提高构件的稳定承载力,此时畸变屈曲往往成为影响构件承载力的主要因素[2-3]。Yang Demao等[4]通过对高强薄壁型钢进行了一系列轴压试验,指出截面形式、畸变屈曲变形以及加劲设置等因素对构件承载力产生重要影响。何子奇等[5]指出局部与畸变相关屈曲的耦合先后顺序对构件的极限承载力和变形影响显著,不能忽视。在实际工程中,冷弯薄壁型钢构件的受力方式常以偏压方式为主,有时还需要对构件进行开孔处理,以便管道、电线等在建筑结构中通过,孔洞及偏心距的存在对冷弯薄壁型钢构件的稳定性能会带来更不利影响[6-9]。以往的研究者主要针对孔洞或偏心对冷弯薄壁型钢构件的力学性能影响开展研究工作[10-11],而关于开孔加劲构件偏载方向的研究鲜有报道。为促进冷弯薄壁型钢构件在工程中的应用,完善国家相关规范,开展此方向的研究工作,具有十分重要的理论意义。
1 有限元模型验证
1.1 有限元模型建立
本文基于沈阳建筑大学徐子风的试验结果[12],选取4根长为1 250 mm的冷弯薄壁卷边槽钢中长柱构件,利用大型通用软件进行数值模拟。选取壳单元进行建模,以构件实际尺寸进行模拟,选取构件计算长度的1/1 000作为最大初始缺陷值,所选取的材料属性、边界约束条件均与试验一致。通过选取6 mm、10 mm、15 mm宽度的网格对部分构件进行对比分析,考虑时耗和精确度等因素,最终选取10 mm网格进行分析。
1.2 有限元模型验证
试验和数值模拟所得的极限承载力和屈曲失效模式对比情况如表1和图1所示。

(a)室内试验 (b)数值模拟
由表1可知:(1)有限元模拟所得的极限承载力与试验值相差均在5%以内;(2)有限元模拟所得屈曲失效模式与试验结果相同。综上分析表明:有限元模拟结果相比试验结果吻合度较高,有限元方法能较好地分析冷弯薄壁型钢偏压构件的力学性能。

表1 试验与模拟极限承载力对比
2 偏载作用下开孔构件有限元分析
2.1 构件腹板开孔设计
按图2的规则对所分析的构件进行编号,其中:L代表试件长度,N代表沿构件纵向的开孔数量,P代表孔洞率,即P=d/H1(d为圆孔直径,H1为长腹板宽度)。构件截面尺寸如图3所示,以构件截面形心作为原点,建立直角坐标系,荷载作用在X正半轴时为正偏心,反之为负偏心,本文共选取9个偏心距,分别为0、±5、±10、±15、±20 mm,图中标注的截面尺寸:H1为150 mm,H2为40 mm,B1为90 mm,B2为25 mm,S为20 mm。按图4所示对构件进行开孔处理,开孔直径d选取45 mm和90 mm。沿构件纵向所标注的参数尺寸见表2。
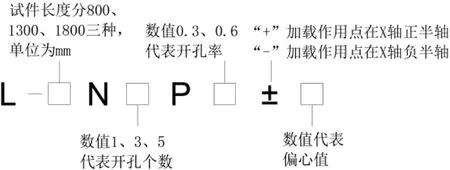
图2 构件编号规则
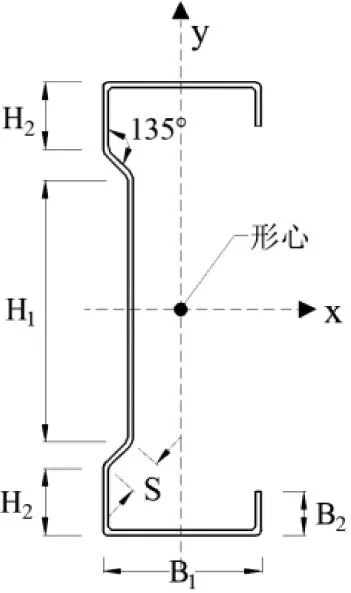
图3 构件截面尺寸
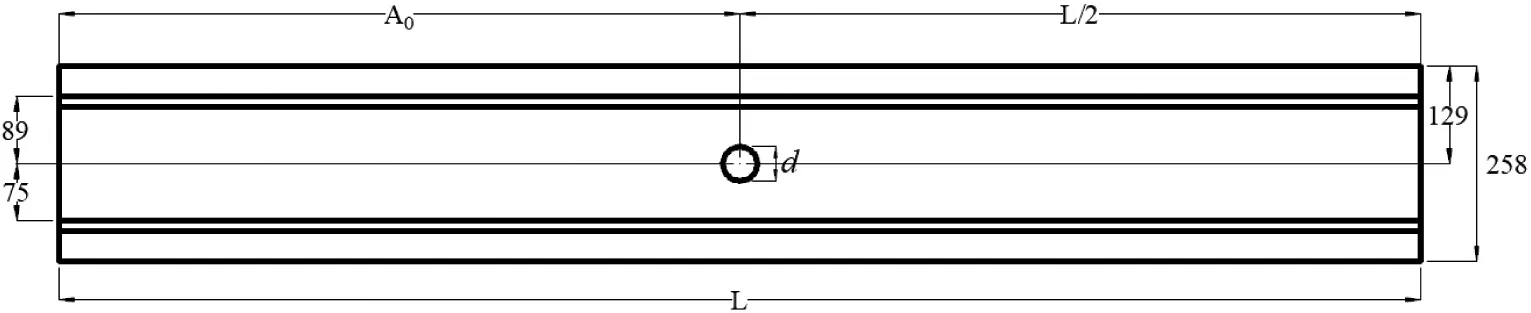
(a)沿构件纵向布设1个孔

表2 孔洞位置参数表
2.2 孔洞对构件屈曲失效模式及承载力分析
2.2.1 开孔构件与未开孔构件对比分析
为对比开孔构件与未开孔构件的稳定性能,选取了部分模拟结果(见表3)。由表3可知:开孔构件的极限承载力均小于未开孔构件,开孔构件的屈曲失效模式与未开孔构件基本相同;当构件处于小偏心时,未开孔构件只发生局部屈曲失稳,而开孔构件发生局部和整体屈曲失稳。

表3 试件极限承载力及屈曲失效模式
2.2.2 偏心距对构件稳定性能的影响
为研究偏心距对构件力学性能的影响,对其承载力、荷载位移曲线以及屈曲失效模式分别进行对比分析,结果如图5~图7所示。由图5可知:随着偏心距的增加,承载力逐渐下降,且构件处于正偏心时,承载力的下降幅度大于负偏心时。由图6可知:荷载位移曲线上升段斜率随着偏心距的增加逐渐减小,且构件处于同一偏心位置时,负偏心的荷载位移曲线斜率略小于正偏心;在荷载下降段,承载力随着偏心距的增加下降幅度逐渐减缓。由图7可知:构件的最大变形多集中在试件的中心位置;当构件处于正偏心时发生畸变与整体屈曲失稳,当构件处于负偏心时发生局部与整体屈曲失稳,且随着偏心距的增加,屈曲变形就越明显;但对于长度为800 mm的构件,受正向大偏心荷载时出现沿翼缘与卷边交线侧向外凸的反常现象。

图5 偏心距对构件承载力的影响

图6 偏心距对荷载位移曲线的影响
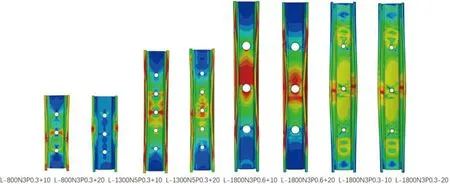
图7 偏心距对屈曲失效模式的影响
2.2.3 孔洞率对构件稳定性能的影响
为研究孔洞率对构件力学性能的影响,对其承载力、荷载位移曲线以及屈曲失效模式分别进行对比分析,结果如图8~图10所示。由图8可知:随着孔洞率的增加,承载力逐渐下降,当构件处于正偏心时,承载力的下降幅度大于负偏心时;小孔径构件承载力与未开孔构件相比基本相同,而大孔径构件承载力与小孔径构件相比偏差较大。由图9可知:在荷载位移曲线上升段,小孔径构件的荷载位移曲线与未开孔构件基本重合,在达到最大承载力时开始出现分岔,而大孔径构件的荷载位移曲线斜率低于小孔径构件;在曲线下降段,随着孔洞率的增加,承载力下降幅度逐渐变大。由图10可知:构件发生沿翼缘与卷边交线侧向内凹的畸变屈曲变形,且内凹程度随着孔洞率的增加逐渐变大。

2.2.4 孔洞数量对构件稳定性能的影响
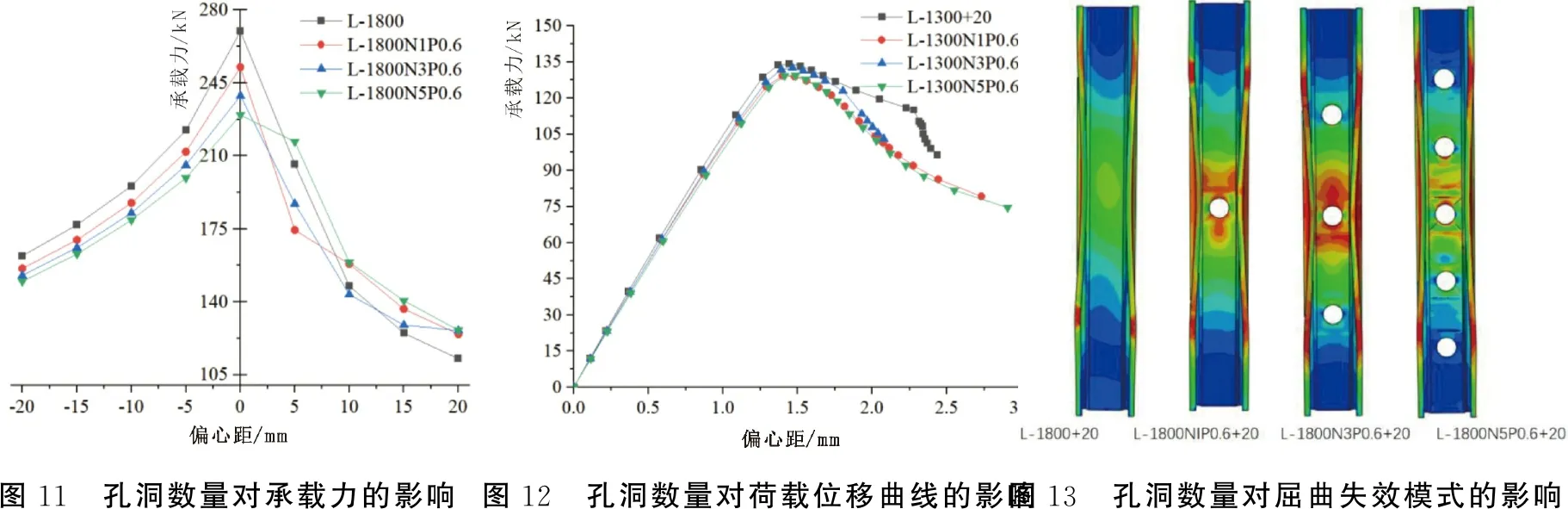
为研究沿构件纵向的孔洞数量对构件力学性能的影响,对其承载力、荷载位移曲线以及屈曲失效模式分别进行对比分析,结果如图11~图13所示。由图11可知:随着孔洞数量的增加,承载力逐渐降低,当构件处于正偏心时承载力下降幅度大于负偏心时。由图12可知:随着孔洞数量的增加,荷载位移曲线在上升段斜率逐渐减小,且在加载中后期曲线出现分岔现象;在荷载下降段,承载力下降幅度随孔洞数量的增加逐渐变大。由图13可知:试件发生沿翼缘与卷边交线侧向内凹的畸变屈曲变形,且随着孔洞数量的增加内凹程度逐渐变大;但构件受偏心距为+20 mm的荷载时,出现内凹程度减小的反常现象。
3 结论
(1)偏心距的存在降低了构件承载力,使荷载位移曲线出现明显分岔,其斜率随偏心距的增加逐渐减小;构件受正偏心荷载时发生沿翼缘与卷边交线侧向内凹的畸变屈曲和整体屈曲变形,且承载力出现上下波动现象,构件受负偏心荷载时发生局部与整体屈曲变形。此外,部分构件受小偏心荷载时只发生局部屈曲变形,长度为800 mm构件在受正向大偏心荷载时出现翼缘与卷边交线侧向外凸的反常现象。
(2)随着孔洞率的增加,承载力逐渐降低,构件沿翼缘与卷边交线侧向内凹程度逐渐变大,荷载位移曲线在上升段斜率逐渐减小,在下降段荷载下降幅度逐渐变大,大孔径构件荷载位移曲线分岔程度大于小孔径构件。
(3)随着沿构件纵向孔洞数量的增加,承载力逐渐降低,构件沿翼缘与卷边交线侧向内凹程度逐渐变大,荷载位移曲线在上升段斜率逐渐减小,在下降段荷载下降幅度逐渐变大。此外,随着沿构件纵向孔洞数量的增加,部分构件受偏心距为+20 mm的荷载作用时,出现畸变屈曲变形减小的反常现象。
