用于智能手机融合定位的行人步长模型研究与实现＊

熊晶

（中国地震局地震研究所，湖北 武汉430071；中国地震局地震大地测量重点实验室，湖北 武汉430071；湖北省地震局，湖北 武汉430071；武汉地震计量检定与测量工程研究院有限公司，湖北 武汉430071）

基于智能手机的增值服务是未来人类娱乐与商业活动的核心增长点，智能手机作为优秀的个人定位导航平台，基于其位置服务的应用具有巨大的社会价值。目前智能手机上已经基本全部配备GPS 芯片，结合行人航迹推算PDR（Pedestrian Dead Reckoning）算法，利用手机传感器测量的步数和估计的步长来估算运动距离，并结合姿态传感器获得航向，从而推算出行人的相对位置[1]，实现复杂环境下行人的导航定位。而其中，步长模型的研究是PDR 算法实现的关键环节，其合理性和可靠性是行人导航定位的重要影响因素。

1 步长估算模型原理

行人步行或跑步过程中，其步长是不断变化的，比如路上步行、转弯、快走、上下楼梯等，步长都不是定值。而且不同行人的步长也是不同的，与行人的性别、身高、体重、年龄、心情甚至个人行为习惯有关[2]。本文仅建立行人在不同场景下的步长模型，暂时不考虑各种用户群体的种类。

目前的研究表明，行人的步长与其加速度的某些统计值有很好的相关性，如最大最小加速度、方差、步频等，目前有4 种步长模型：常数步长模型、线性步长模型、非线性步长模型和神经网络步长模型[3]。

常数步长模型是最简单的步长模型，假设步长为常数。常数由手机GPS 定位结果计算得出，当没有GPS 信号时，步长默认为最后一次GPS 定位计算的结果：

式（1）中：Sk为k 时刻步长；SGPS为GPS 实时计算的步长；wG、ws是高斯白噪声；S0为GPS 无信号之前定位结果计算的最后步长。

虽然在室外GPS 定位精度最好，但仍然有10 m左右的误差，所以据此计算的步长精度很难到达米级，而且误差积累更大。

线性步长模型认为步长和步频、加速度之间存在线性关系[4]，为：

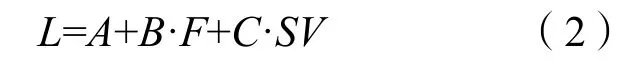
式（2）中：L 为步长；A、B、C 为线性模型系数，可由实验线性模拟得出；F 为步频，即该步所用时间的倒数；SV 为该步的加速度方差。

非线性步长模型是通过步行过程中加速度的最大值和最小值为参数建立的，优于难以证明步长和运动参数的线性关系，所以线性关系只是一种简单估计，而步行过程中的加速度是在不断动态变化的，总有2个极值的存在。所以有学者提出基于加速度极值的模型公式：

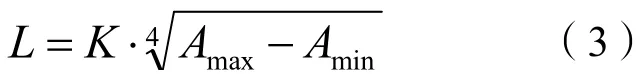
式（3）中：K 为模型的系数；Amax是该步过程中最大的加速度值；Amin为最小的加速度值。

人工智能步长模型不是建立步长与运动参数之间的关系，而是将运动数据作为样本输入，进行反复训练，自适应估算出步长，比如输入该步的加速度最大值、加速度最小值、方差及步频等。最后，通过神经网络学习算法，估计出步长[5]。

3 种步长估计模型的比较如表1 所示，这3 种步长估计模型线性估计模型效果最好，所以本文拟选用线性估计模型，通过最小二乘法线性拟合求出线性估计模型参数A、B、C。

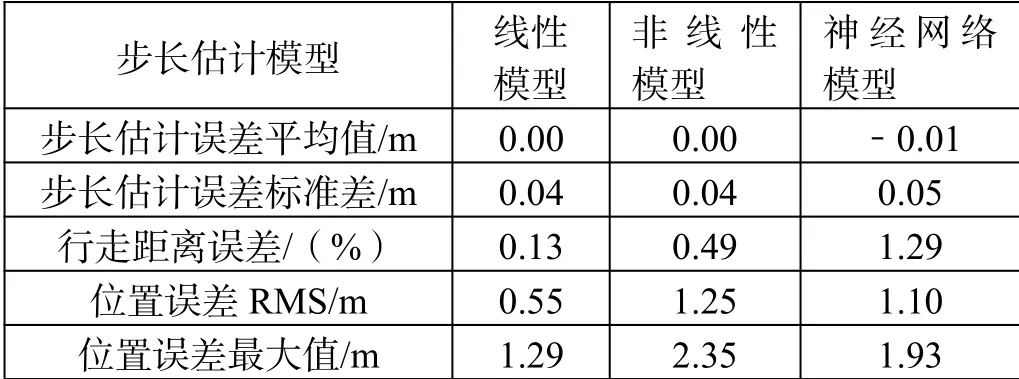
表1 3 种步长估计模型的比较

2 最小二乘法拟合线性步长模型

最小二乘法拟合是以最小化误差平方的思路来得出数据的最佳匹配函数，利用最小二乘法可以拟合出未知数据，并使其与实际数据之间误差的平方和最小[6]。

步长线性估计模型可表示为：

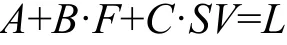
假设有n 组实验数据（n 至少为3），每组数据都是由GPS 和步数计算的步长、步频F、加速度方差SV组成，设A、B、C 为参数X，并给定估值，组成n 个观测方程，利用最小二乘间接平差的原理，可得出以下公式：

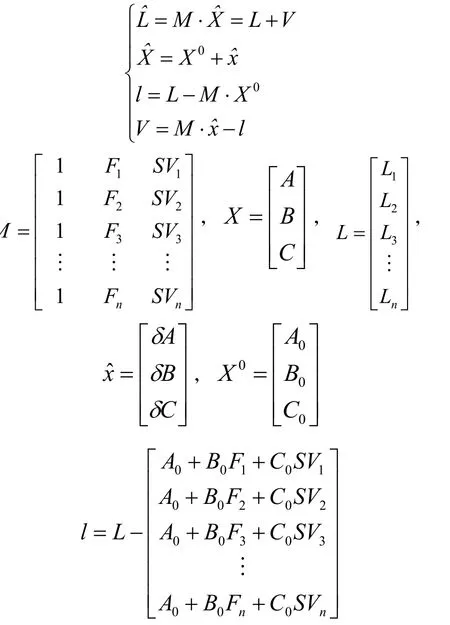
A0、B0、C0为近似值，根据最小二乘原理，VTV=min，最优解为，参数协方差

根据实验得出步行状态模型参数结果，考虑到实际情况，用户在使用计步软件之前一般不会专门做实验来求出精确步长模型，所以本文设计了一个通过后期训练方式的模型建立算法。前提条件是用户首次使用定位软件是在GPS 信号良好的情况下进行，因为融合定位需要GPS 定位结果作为初始值。用户在GPS 定位精度较高的情况下，行走一段距离，记录步数和每一步的加速度方差及步频等参数，然后通过距离和步数计算步长，最后拟合一次线性步长模型求取A、B、C 的参数值。

算法流程是在室外GPS 信号良好情况下，每5 步估算一次步长L，通过每步的起始位置和结束位置求取GPS 定位距离估算，这里假设5 步步长一样，并记录平均加速度方差SV 和平均步频F；然后每走20 步，拟合一次步长模型，有4 个步长模型方程，计算出参数A、B、C。然后和下一个20 步步长模型求取参数的平均值，当步数积累足够多时，模型参数会越来越准确，在收敛到一定精度后，就不再继续模拟，具体流程如图1 所示。

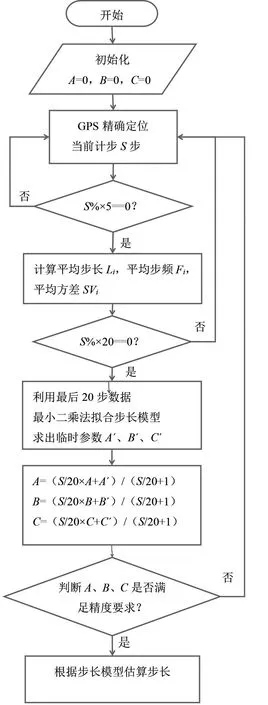
图1 后期训练步行估计模型算法流程图

3 计步器原理和功能实现

3.1 人体步行规律

在能够准确测量步数之前，需要了解人体步行瞬间动作。人体步行动作分解如图2 所示，人体在连续正常行走过程中，总是会按照图2 流程循环进行。首先是身体向前倾斜，准备迈出左脚，左脚跟离地，即认为是一步起点。身体向前倾斜后会有向下跌倒的趋势，此时右脚尖会蹬地，以便左脚抬起后迈出，使人体重心前移并上升。然后左脚摆至一步的距离落下，左脚跟着地，重心前移并下降。最后左脚尖着地，右脚往前收回，直至与左脚平行，计作一步。下一步是右脚继续向前迈出，重复上述动作[7]。

图2 人体步行动作分解

3.2 计步器原理

目前，计步器得到了广泛的研究和应用。早期是计步器硬件，随后是手机等移动设备的计步功能，到现在流行的穿戴设备如手环计步等，其原理都是通过采集加速度传感器的数据，进行数据的峰值检测。

鉴于人体行走时，手机的姿态是随机的，手机的三轴加速度不能取某一轴来代表竖直方向的加速度变化，所以应随三轴加速度数据取模，利用三轴的合加速度进行步态分析。步行状态加速度数据有明显的周期性变化，而且一个周期刚好是一步，一步的周期里有一个大波峰、一个小波峰以及一个波谷，所以只要能检测出一段时间内的大波峰数量，就可以估算步数。

本文的计步原理是通过设置一个检测窗口，计算窗口内的合加速度方差，然后根据设定阈值，判断该窗口内步行的行为，从而判断是否为一步。根据人体步行规律，此处设置2 种阈值：一种是检测是否达到大幅迈步时期的加速度方差阈值T1，另一种是检测是否达到脚和地面接触站立时期的加速度方差阈值T2[8]。

其算法步骤如下。

第一步，每个采样点都要求算出合加速度ai：

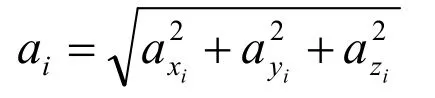
第二步，计算滑动窗口w（w=15）内的合加速度平均值：

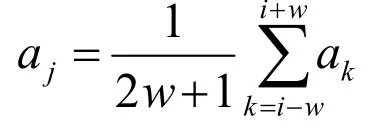
第三步，计算w 窗口内的方差：

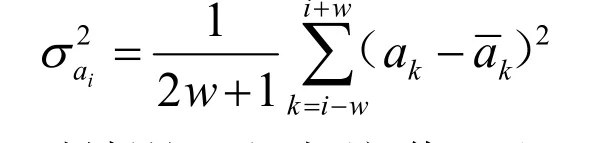
第四步，判断是否达到了阈值T1和T2。

判断为一步必须满足以下2 个条件：①迈步时期必须是从高加速度向低加速度转变；②在当前样本i之前窗口大小w 之中，至少有一个低加速度被检测到。

考虑到人体步行或跑步的情形下，正常人的步频会在1～5 Hz 范围内变化，也就是0.2～2 s 走一步，如果某一步的步频不在此范围，可以认为是错误判断，这样可以提高计步的准确度。而且根据香农定理，采样频率应至少达到最大频率的2 倍。

4 步数探测实验

本实验分别行走了具备不同路面的路段，标准步数为100 步，均是直线行走，为了验证本文计步算法的性能，实验测试了5 组，结果如表2 所示。

从统计结果来看，本文计步算法准确性较好，平均准确率为97%，平均误差为-1.4%，最大误差仅为-6.0%，充分验证了本步数探测算法能够有效地探测步数。但本算法很难避免错误计步，可能是因为手机在其他情况下，也会计步，比如手动摇晃，计步算法也会增加步数。但总体来说，该计步算法能够满足融合定位的行人航迹推算要求。

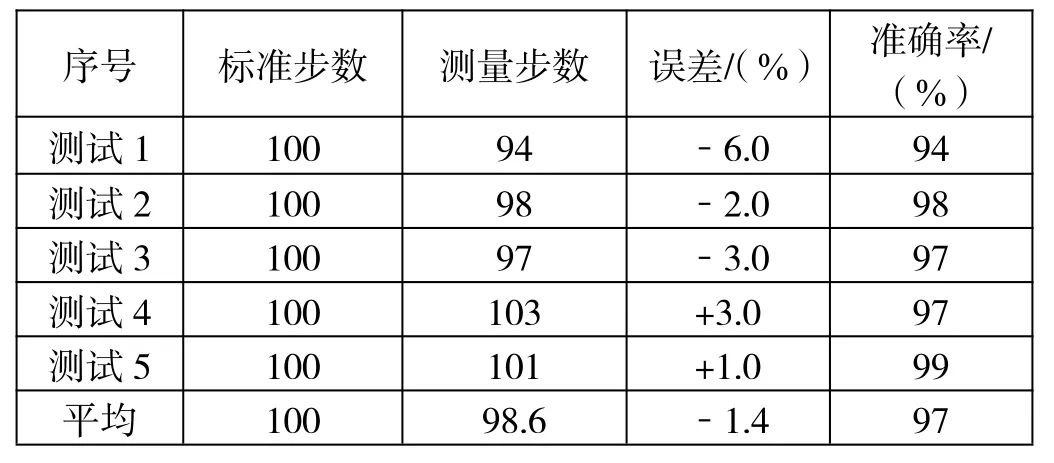
表2 步数探测实验

5 结语

本文介绍了步长估算模型的原理，通过最小二乘法拟合线性步长模型。介绍了人体步行规律和计步器的原理，设计了一种适合智能手机融合定位算法的步长模型，通过实验验证，证明本步长模型能够满足融合定位中行人航迹推算的要求。