装箱算法在卷烟配载验证系统中的应用

王 玮，张洁华，张菡子，李景舒，季靖寒

（上海烟草集团有限责任公司上海烟草储运公司，上海 200439）

1 研究背景和意义

随着上海烟草集团产销规模的扩大，客户对卷烟的需求朝着多样化、小批量、多频次和个性化方向发展，不仅花式烟品种规格增加，拼车订单也逐年递增，导致卷烟配载业务的复杂程度与日俱增。在卷烟单车配载环节，长期以来都是依赖人工经验进行的，对于是否已经达到运输车辆使用率的最大化、配载效益的最大化无从评估，同时这种配载方式强烈依赖员工的个人能力和经验，不利于大规模推广[1–2]。在面临日益复杂的配载要求时，人工耗时变长，单车满载率降低，若是导致翻箱，会极大浪费人力成本、时间成本。因此，有必要设计一种烟草配载验证系统，根据烟草订单信息、车辆信息以及各类件烟规格信息等，对人工设计的配载方案进行验证并生成装车图，指导工作人员进行装车，用于替代目前基于经验的人工配载方式，达到有效减少装车时间、提高装车效率，提高单车满载率和装车一次成功率，从而达到降低物流成本，提高经济效益的目的。

2 卷烟自动配载及验证系统

卷烟自动配载及验证系统可以根据烟草订单信息、车辆信息、各类件烟规格信息等生成卷烟装车图，也可以输入人工配载方案进行验证并生成装车图，以指导工作人员进行现场装车。系统功能框图如图1所示，文章重点介绍了配载验证功能模块中的卷烟装车验证算法。

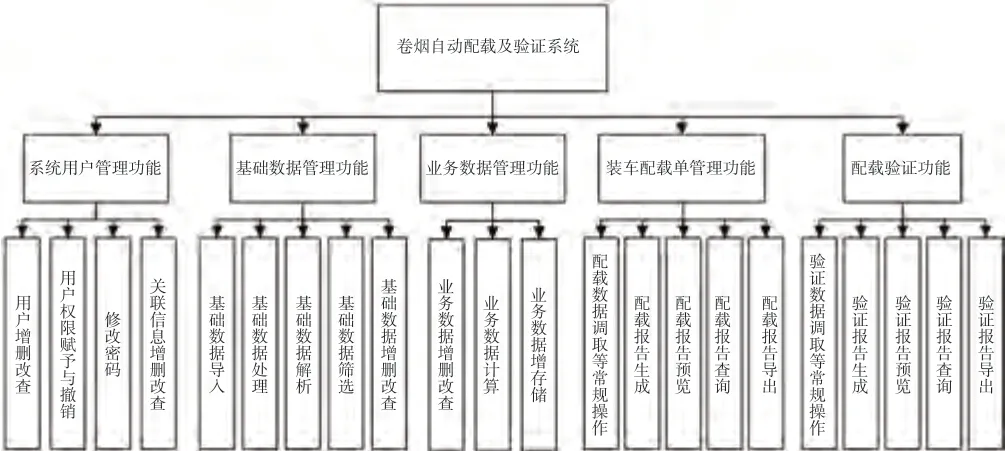
图1 卷烟自动配载及验证系统功能框图

3 卷烟装车验证算法

装车验证算法是对人工设计的配载方案，即人工选出需要运输的货物和运输这批货物的车辆，在正式运输之前验证其准确率，降低翻箱率。这在本质上是三维装箱问题，给定一些不同类型的箱子和不同规格的容器，如何将所有的箱子装入最少数量的容器中[3–4]。

装车验证算法的核心是启发式拟人装箱算法。解决这类利用计算机帮助人工或优化人工操作的实际问题，通常借鉴丰富的人工经验，使计算机通过拟人的方式解决问题是非常有效的[5]。在实际的装箱过程中，人们通常会在车厢内一角开始放置，先装满一行，再在一行的基础上向上放置装满一面，最后从车厢内侧到外侧依次装满整个车厢。受人工装箱方式的影响，在算法的装箱过程中，通过设定初始放置点放置箱子，下一个箱子的放置位置通过查找放置点集合进行确定，并通过对放置点集合进行排序完成从车厢内侧到外侧的放置过程。

3.1 放置点

可以将车厢看成一个三维坐标系，将车厢内侧右下角坐标（0，0，0）作为初始放置点并存入放置点集合，放置一个货物后会生成3个新的放置点，并存入放置点集合中。设车厢的长宽高分别为H，W，D，货物的长宽高分别为h，w，d，则生成的3个放置点分别为（h，0，0），（0，w，0），（0，0，d），如图2所示。

图2 货物产生的三个放置点

因为需要将货物按照从车厢内侧到外侧的顺序放置，则需要对放置点集合进行排序。通过对放置点按照先y 轴从低到高，再z 轴从低到高，最后x 轴从低到高的顺序完成对放置点的排序，完成实际的装箱效果。

3.2 装箱约束条件

3.2.1 方向约束

货物在车厢内部一共有6种放置方向，但是根据人工的装箱经验，为了保证烟草在运输过程中不会出现倒丝的现象，实际货物的放置过程中只会出现4种方向，分别是方向1（h，w，d），方向2（w，h，d），方向3（h，w，d），方向4（d，h，w）如图3 所示。方向1是将货物的长边作为h也就是长，而短边作为宽w，这样的放置方向可以保证车厢的宽度得到最大利用。当方向1放置货物在车厢内长度无法满足时，则使用方向2调转货物长和宽，使得车厢内的长度得到最大利用。当方向1放置货物在车厢内高度无法满足时，使用方向3或方向4，将货物水平放置，使得车厢内的高度得到最大利用。

图3 四种放置方向

3.2.2 重叠约束

每一个货物的放置位置是根据之前放置货物产生的放置点确定的。但是同一车厢内会运输不同种类的货物，其规格是不一致的。这样货物在放置过程中会出现间隙，从而导致计算机在放置货物时会出现重叠的情况。如果两个货物没有发生重叠，这两个货物之间的相交面的个数是0代表不相交或者是1代表相邻放置，但是如果两个货物之间发生重叠，则这两个货物之间的相交面的个数一定会超过两个。利用这一规则设计重叠检测条件，当货物之间的相交面个数小于等于1时允许放置，否则认为其相交取消放置。

3.2.3 悬空约束

计算机在计算货物的放置位置过程中，某些放置点可能会因为货物之间发生重叠或其他原因而取消放置，导致接下来的货物可能会出现悬空的情况，这是违反实际物理条件的。因此，需要设置悬空检测条件。通过计算放置点和货物规格以及之前已经放置的货物之间的高度信息来判断货物是否悬空，满足条件则放置，否则会计算悬空货物与其底部最近货物之间的高度，在不违反约束条件的情况下将悬空货物落到离其底部最近的货物上。

3.2.4 行间约束

实际装箱过程中因为货物种类的不同，若两种货物之间不加以约束而直接根据放置点集合中的位置放置，会出现货物放置位置混乱，车厢内空间利用率降低，不利于货物的稳定运输。所以需要设计行间约束条件，保证货物放置过程中每一行的整齐。主要约束条件有，若下一批货物的长度超过了其底下已经放置好的货物长度，则会判断货物的宽度和其底下货物长度之间的关系，若小于则按方向2进行放置，若还是超过底下货物的长度则改变货物的装载顺序，并且货物的上方只能放置一件货物，除非多件货物的长度不会超过其底下的货物。当货物因行间y轴长度不一致发生货物重叠的情况时，会记录此时已经放置的货物的y轴最大值和因重叠而无法放置货物的放置点的x值，并依据这两个值生成新的放置点存入放置点集合中，增大空间利用率，保证接下来货物放置的整齐。

3.3 装箱算法

基于上述放置点的生成方法和约束条件，可以得到用于配载验证系统的三维装箱算法。算法设货物集合为B={b1，b2，…，bn}，放置点集合为items，其初始值为（0，0，0）用于确定第一个货物的放置位置，算法的返回值是一个集合output 代表已经放置货物在车厢内的坐标和货物种类。算法流程图如图4所示。

图4 装箱算法流程图

在该装箱算法中，首先分别从货物集合B 和放置点集合items 中取出需要的数据，之后根据取出的货物bi（i ∈1，…，n）的规格以及放置点的位置判断其在方向1的情况下能否装入车内。若可以装入则判断货物bi与其他货物是否发生重叠，若发生重叠但是因为行间长度不一致导致的重叠则会根据行间约束规则生成新的放置点并存入集合，否则不对该放置点进行放置。若没有发生重叠则判断货物bi是否悬空。若不悬空并且bi的长度小于其底部货物的长度则在此放置点进行放置并生成新的放置点，再去除下一个放置点和货物，判断货物集合是否装完。否则按照相应的约束规则进行放置。若方向1无法放置货物则判断方向2是否可以装入，若可以则判断相关的约束条件是否成立执行操作，否则判断方向3是否可以装入。若3个方向都无法装入货物则该放置点不进行货物放置，取出下一个放置点。当货物集合全部装完返回货物在车厢内的坐标和货物种类并存入output 中。配载验证系统根据output 来绘制所需的装车图。

4 测试结果

使用两天内的实际订单装车数据来进行配载验证功能模块的测试，部分测试结果如下表1所示，测试结果表明卷烟装车算法可以成功验证人工配载订单。

表1 测试结果

5 结束语

文章设计了一套基于人工经验的卷烟装车验证算法，装车时可以充分利用车厢的长宽高，提高单车满载率。通过配载验证功能模块可以对人工配载订单进行验证，从而提高卷烟装车效率，保证装车一次成功，杜绝翻箱现象。由于考虑装车过车中卷烟的稳定性，导致货物之间会产生一定空隙从而浪费一定的体积，因此该算法还需要进一步研究和优化。