计入用户从众心理的分布式光伏装机容量预测
2022-07-26吴璐阳辛洁晴王承民
吴璐阳,辛洁晴,王承民
(1. 电力传输与功率变换控制教育部重点实验室(上海交通大学),上海市 200240;2. 国网福建省电力有限公司电力科学研究院,福建省福州市 350007)
0 引言
随着分布式光伏并网规模的不断扩大,光伏装机的精准预测对电网的发展规划和安全运行具有重要意义。分布式光伏的发展不仅受经济实力、安装条件、技术水平等因素影响,还与政策的激励密切相关。例如,2001—2013 年间,在固定上网电价(feedin-tariff,FIT)的政策激励下,德国光伏曾在2010—2012 年3 年间年新增装机容量均超过7 GW[1];2014年,德国修改《可再生能源法》并下调FIT 后,导致后续年份光伏装机容量增速的大幅度下降,年新增容量均不超过2 GW[2]。目前,中国现有激励政策针对“全额上网”和“余电上网”两种光伏并网方式分别给予补贴激励,近年政策的调整对光伏投资产生了显著影响[3]。
现有研究中,计入激励性政策对光伏装机容量影响的预测多为机理性预测,且以动力学方法[4]为主。例如:文献[5]利用系统动力学模型模拟政策影响下中国光伏发电的长期发展格局,指出目前光伏产业主要收益来自补贴而非发电;文献[6]基于光伏产业的利润和成本预测模拟政策的动态演化过程,并将演化结果应用于光伏的系统动力学预测模型中;文献[7]通过对投资回报率和FIT 的组合分析,利用系统动力学方法评估各类激励性政策效益。上述研究均假设用户为绝对理性的投资者,以投资收益最大化为目标实施分布式光伏的投资决策。
分布式光伏产业是一种新兴产业,收益受政策影响较大,用户的投资行为因从众心理表现出一定的非理性现象。目前,在分布式光伏投资决策或装机容量预测中计入从众心理的研究尚未见报道。在金融、消费者行为等其他领域,从众行为的影响已有一些研究,例如:文献[8]对股市投资者的从众行为进行分析,发现投资行为受个体主观偏好和网络群体效应的共同作用;文献[9]运用复杂网络描述从众心理和收入水平对消费者低碳行为的影响。鉴于从众心理本质上反映用户与其周边用户的信息交互对其决策行为的影响,相关研究中多用网络模型模拟社会交互状态,并发现个体从邻近周边获取信息的小世界网络是社会关系的普遍特征。例如,文献[10]利用二分网络法构建基金市场信息交互网,发现该网络具有小世界网络特点;文献[11]构建了股市投资网络模型,通过度分析和平均路径分析,发现投资者关联网络也具有显著的小世界特征。
鉴于此,本文在分析光伏投资从众心理表现的基础上,基于系统动力学模型提出了一种地区分布式光伏装机容量预测方法。与以往方法不同的是,本文构建了模拟光伏投资信息交互的小世界网络,以模拟分析出用户对分布式光伏的从众投资概率,并在系统动力学模型中引入计及从众心理的光伏装机意愿模块。针对光伏投资受投资回报率的理性思维和从众心理的非理性思维的双重影响特征,由投资回报率所反映出的初始装机意愿和受从众心理影响的附加意愿共同决定用户光伏装机意愿,以此确定光伏新增投资量。算例部分检验了所提方法对光伏预测精度的提升效果,分析了小世界网络参数对预测效果的影响,并分析了光伏发展不同阶段从众系数的选取原则。
1 光伏投资决策中从众心理的表现
在新兴产业发展中,当投资者对产业政策预期不明朗时,更易观望他人行动,参考周围人群的决策(投资/不投资)而做出与周围多数人相同的选择,是投资从众心理的一种表现。
为考察分布式光伏投资中的从众心理表象,观察中国南方A 市和德国历年光伏投资回报率与光伏新增装机容量情况(见图1 和附录A)。从中可得出如下几种从完全理性用户角度难以解释的现象。
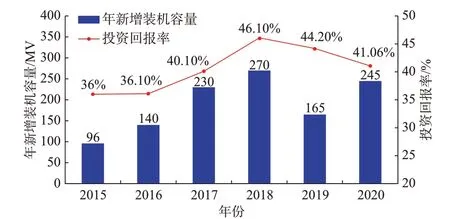
图1 2015—2020 年中国南方A 市分布式光伏投资回报率与新增装机容量Fig.1 Return rate of investment and added installed capacity of distributed photovoltaics in city A in southern China from 2015 to 2020
1)产业发展初期的高额补贴不一定立刻带来产业的大发展。以图1 情况为例,自实施“余电上网”的全电量补贴和“全额上网”的光伏标杆电价后,2015—2016 年间激励政策基本不变,分布式光伏的投资回报率保持在36%,远高于其他很多领域的投资回报率,但由于投资者对产业政策可能产生的收益尚不明朗,这两年光伏投资并没有呈快速增长趋势,两年共新增分布式光伏装机容量年均只有236 MW。直到2017 年,当投资者初具规模,分布式光伏新增装机容量才呈快速增长,当年新增装机230 MW,类似现象在德国2005—2008 年间也有体现。该现象说明,光伏产业发展初期的高额补贴不一定立刻带来产业的大发展,由于投资的用户较少,大多数用户处于观望状态,导致产业兴起有一定的滞后度,这是从众心理的一种表现。
2)投资回报率处于高位期时,回报率小幅振荡并不会引起投资随之波动,投资仍会迅猛增长。例如,德国2009—2012 年间的光伏投资回报率一直处于高位(70%以上),其中,2010 年的投资回报率略有下降,但光伏新增装机达7.2 GW,甚至超过投资回报率较高的上一年的新增装机容量。这说明在高回报率期,随着光伏投资者的增加,越来越多用户愿意投资光伏,可能做出偏离回报率趋势的决策。这是从众心理的又一个表现。
3)当投资回报率处于下降期,光伏投资会以比回报率下调速度快得多的速度减少。例如,德国2013 年的光伏投资回报率比上一年略有下降,但还远远高于2011 年以前的水平。然而,因当年已在讨论FIT 方案的修订,民众对光伏产业前景的评估大不如前,使得当年光伏新增装机容量大幅回落,下降幅度达到了51%。这也是从众心理的一种表现。
上述分析表明,光伏新增装机容量与投资回报率之间有偏离简单正向关联关系的复杂关系,计入从众心理可为这种关系提供一种合理解释。因此,在光伏装机容量预测中计入从众心理的影响是一个值得研究的问题,有助于提高预测精度。
2 小世界网络
社会关系可由网络模型来描绘,节点代表决策者个体,连边代表个体间的信息交互关系[12]。现实世界中,个体总是较易与邻近周边的个体发生信息交互并受其影响,故而表现出高聚类系数、低路径长度的小世界网络特征[13-14]。以随机化重连为核心步骤的小世界网络由Watts 和Strogatz 提出,故而最初的小世界网络模型又称为WS 模型。
本文采用如下步骤生成模拟光伏投资信息交互网的WS 模型[15]:
1)构建“近邻耦合网络”:设网络内包含N个节点,用边将每一节点i与其最相邻的M个节点连接起来,此时所生成的网络称作“近邻耦合网络”,其中的每条边称作“短边”。
2)随机化重连:在0 至ki(ki为节点i上的关联节点数)的范围内,以重连概率p随机断开短边;再采用随机数生成法,从未与节点i相连的剩余节点中选出节点,与节点i重新相连,由此形成新的连边(称为“长边”)。上述过程中,确保不同节点之间最多通过一条边相关联,并且每个节点均不与自身相关联。p的取值范围为0~1,当p取值较小时生成的网络具有小世界网络的特征,本文p取0.07[12]。
WS 模型是对现实世界的缩小版仿真模型,通常取节点数N=100 就可实现对现实社会关系网络的良好模拟[9];并且,WS 模型描述的是由社会关系决定的信息交互网,不随预测年动态调整。对后续研究而言,生成的WS 模型确定了每一节点上的关联节点数ki,该值随机生成,但WS 模型的统计学特征由网络生成参数N、M和p决定。在取N=100、M=3、p=0.07 的情况下,生成描述光伏投资信息交互关系的WS 模型见图2。由于从众心理对光伏投资影响分析中考虑的是已投资者对潜在投资者影响的群体效应,WS 模型具体形式对预测结果影响不大。

图2 描述光伏投资信息交互关系的WS 模型Fig.2 WS model describing interaction relationship of photovoltaic investment information
3 光伏装机容量预测
3.1 光伏装机预测系统动力学模型
本文通过建立系统动力学模型进行光伏装机容量预测。模型的存量流量如图3 所示,包含“光伏饱和和潜在装机容量”“光伏发电成本”“光伏并网模式决策”“投资回报率”“光伏装机意愿”“年新增装机容量”6 个模块(图3 中每一虚线框对应一个模块,顺序编号为①至⑥)。与一般的系统动力学预测方法相比,该模型在“光伏装机意愿”模块(编号⑤)加入了从众效应子模块(红色框部分),以反映用户光伏装机意愿受从众心理的影响。

图3 计入用户从众心理的光伏装机预测系统动力学模型Fig.3 System dynamic model of photovoltaic installation forecasting considering users’herd mentality
系统动力学模型用于光伏装机容量预测时,输入数据包括基础年光伏装机容量、基础年光伏投资回报率、预测期每年的光伏政策(若未来年政策不明朗,则输入基础年光伏政策)、各种性质(居住/工业/商业)用地的面积,以及模拟光伏投资信息交互关系的WS 模型。预测是逐年递推的过程,对第y年预测时,各模块之间的作用机理如下:
1)影响用户理性决策的光伏投资回报率、用户经济实力、安装条件等因素以及非理性因素——从众心理,共同决定了用户对光伏的综合投资意愿,该意愿表现为一个地区某年的光伏新增容量与可开发容量(本文定义为“光伏潜在装机容量”)之比。因此,可通过分析当年光伏潜在装机容量和光伏投资意愿,并将两者相乘,得到第y年新增光伏容量预测值。为此,模块①首先评估第y年光伏潜在装机容量,该值由地区用地构成和各类用户的光伏安装条件决定。
2)在预测期用户经济实力和安装条件基本不变的假设下,第y年投资意愿由当年光伏投资回报率和用户从众心理决定。对前者,先由模块②根据上一年光伏累计装机容量,按一定学习率模拟光伏成本的衰减过程,评估第y年投资的光伏的平准化度电成本,作为投资回报率计算的基础数据;随后,注意到中国对“余电上网”和“全额上网”两种光伏并网方式的补贴和上网电价政策不同,在模块③中根据可预见的第y年光伏政策,对当年用户会选择的并网方式做模拟决策;再由模块④按并网方式测算投资回报率,进而确定由投资回报率决定的那部分投资意愿(称作“光伏初始装机意愿”)。
3)对从众心理影响部分,模块⑤首先用WS 模型模拟光伏投资的信息交互,分析出潜在投资者获取周边用户的投资信息而做出光伏投资决定的概率,由此产生的投资意愿称作“从众心理附加意愿”。模块⑤将初始装机意愿与从众心理附加意愿相加,得到第y年光伏综合装机意愿。
4)光伏综合装机意愿决定了第y年光伏潜在装机容量中可能投建的容量比例,故而最后由模块⑥将潜在装机容量与光伏综合装机意愿相乘,得到第y年光伏新增容量预测值,并将该值与第y-1 年光伏累计装机容量相加,得到第y年光伏累计装机容量,作为下一年预测的基础数据。
3.1.1 地块光伏饱和和潜在装机容量
地块用地规划和地理条件决定了该地区可开发光伏水平的上限,即光伏饱和装机容量[16]。现有用地类型主要可分为居住用地、非工非经营性与商业用地、工业用地3 类用地,本文对研究区域的3 类用地分别进行预测,最后将3 类用地的预测结果相加,得到目标地区光伏总装机容量预测值,故以下隐去表征用户类型的下标。
设某类用地的建筑基底面积为fbuilding,建筑屋顶比例为kroof,则该类用地的建筑屋顶投影面积froof为:

3.1.2 年新增装机容量
目标年潜在装机容量中有多少会安装与当年用户光伏装机意愿的强弱有关,装机意愿越强则安装容量越大。若用新增装机容量ΔPpv(t)与同年分布式光伏潜在装机容量的比值来定义用户光伏装机综合意愿ζpv(t),则该年新增装机容量可表示为:

式中:Cini(t)、Cop(t)、Cloan(t)分别为在目标年t投资分布式光伏系统平准化后的投资成本、光伏系统的运行维护费用和贷款投资计入的利息。
光伏静态投资与产业技术发展呈现出负相关规律。本文模型利用学习曲线模拟光伏平准化投资成本的下降规律[15],光伏系统静态投资成本的变化趋势可表示为:
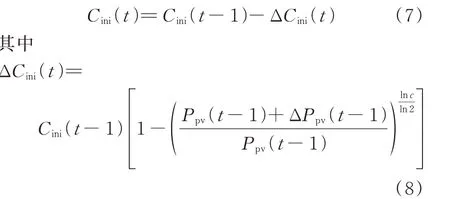
式中:ΔCini(t)为第t年分布式光伏单位静态投资成本的减少量;c为学习率,依据中国分布式光伏发展趋势拟合得出光伏静态投资成本的学习率为22%~34%[17]。
式(6)中,年维护成本Cop(t)与静态投资成本相关,基于光伏系统的固定运维费率λop,Cop(t)可表示为:

式中:φloan为分布式光伏系统贷款占建设成本的比例;τloan为光伏项目的贷款利率。
3.1.4 光伏并网方式决策


式中:Wpv为每个用户在分布式光伏全生命周期内的年均发电量,该值与预测目标年t无关;ω为光伏“余电上网”模式下自发自用部分的电量比例;L为对应用地类型的典型用户年均用电量;e1(t)为“余电上网”的全电量补贴;e2(t)为“余电上网”电价;e3(t)为“全额上网”电价;e4(t)为用户的购电电价;上述4 个政策性参量以基准年值代入,若据基准年已颁布文件可知预测目标年t的取值,则用第t年数值代入。
设用户投资光伏时并网摸式的选择通过μ表示,该值采用布尔型变量表征用户的并网决策是否为“余电上网”模式。以投资效益最大为目标,以μ和ω为变量的并网方式决策模型为:

3.2 计入从众心理影响的光伏装机意愿模块
本文将用户未受从众心理影响而完全由投资回报率决定的装机意愿称为“初始装机意愿”(记为ζini(t))。另一方面,处于观望状态的用户通过信息交互了解其他用户的光伏投资信息,因而可能做出投资光伏的决策,由此产生附加装机意愿,称作“从众心理附加意愿”(记为ζg(t))。光伏装机意愿模块对这两部分投资意愿进行测算,并将其相加,获得式(5)中的光伏装机综合意愿ζpv(t),进而决定目标年新增光伏装机容量。
首先,在不计从众心理的条件下,以基准年新增装机容量与该年潜在装机容量之比作为初始装机意愿基准值ζpv0,该意愿值是目标地区在基准年的用户经济实力、安装条件、光伏投资回报率等多种因素综合作用的结果。假设预测期用户经济实力、安装条件基本不变的条件下,初始装机意愿仅受光伏投资回报率的影响,并与投资回报率成正比。因此,若设基准年的投资回报率为Rpv0,可用如下线性关系表述第t年的初始装机意愿ζini(t):

用户受到关联投资者决策信息的影响而产生与群体行为趋同的现象。若来自群体的影响力越大,则投资者与群体行为的趋同性越高,因此引入从众系数τ反映群体效应对用户投资决策影响的大小;在用户i的ki个关联用户中,决定投资分布式光伏的用户数a有0 至ki种可能。因此,目标年t处于观望态度的用户i受从众心理影响而更改其光伏投资决策的概率βi(t)为:


综合式(17)和式(18)可见:一个地区有越多的用户已经选择投资光伏,则在从众心理影响下该地区光伏装机的群体效应越明显,此时ˉβ(t)越接近1,光伏综合装机意愿ζpv(t)就越接近于1。反之,一个地区已投资光伏的用户数越少,则ˉβ(t)越接近0,光伏装机意愿ζpv(t)就越接近于ζini(t)。将式(20)确定的ζpv(t)代入式(5),便获得计入从众心理影响的分布式光伏新增装机容量预测结果。
4 算例分析
针对图1 所示中国南方A 市相关情况,采用所提方法对该市3 类典型用户分别进行光伏装机容量预测,对3 类预测结果求和后获得分布式光伏总装机容量预测值。本文系统动力学模型通过Vensim PLE 软件仿真搭建。
4.1 算例参数
依据基础年A 市3 类用户光伏装机容量统计值和用地远景规划面积,确定不同类型用户的分布式光伏饱和装机容量,如表1 所示。其中,居住用地、非工非经营性与商业用地、工业用地的kroof取值分别为0.85、0.90、0.95,屋顶光伏可利用系数分别取值0.45、0.25、0.6;基于A 市地理情况,年光照峰值小时数为1 291.29 h[16]。
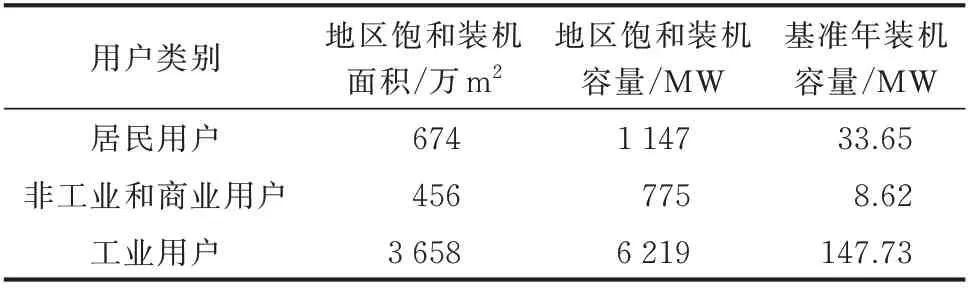
表1 中国南方A 市光伏装机条件与基准年装机情况Table 1 Photovoltaic installation conditions and base year installations in city A in southern China
统计显示,A 城10 kV 及以下3 类用户的平均每户年用电量分别为2.422 6、123.3、3 901 MW·h,预测目标年的用电量按Logistic 模型进行调整[18]。该市零售电价以分时电价为主,在统计典型用户典型日分时用电比重的基础上,算得3 类用户平均购电价分别为0.617、0.951、0.750 元/(kW·h)。
光伏系统的平均寿命为25 年,预测选取基础年的单位静态投资成本为0.774 元/(kW·h),考虑金融成本的资金折现率为7%[17];分布式光伏配置储能后运维费率λop将有所上升因此取值为5%;模拟静态投资成本的学习曲线模型的学习率c取值为28%;贷款利率按6%计入,光伏融资方案中贷款部分占比取50%[19]。
N=100、M=3、p=0.07 时,所生成的WS 模型与投资网络平均特征值最为接近[9],因此,选取上述参数构建小世界网络。取从众系数τ=0.5。
4.2 计入从众心理的光伏装机容量预测结果
采用本文方法对2016—2020 年A 市分布式光伏装机容量进行预测。采用两种时间跨度:1)预测期为1 年,鉴于文件发布时会预告新政策开始时间,故假设每年末根据当时光伏累计装机容量和可预知的次年光伏政策进行预测,逐年滚动至2020 年;2)预测期为5 年,此时虽然系统动力学模型也是逐年滚动预测,但预测基准是由逐年光伏累计装机容量预测值和基准年获知的光伏政策决定的,该方式更符合中长期预测的特点。对于两种时间跨度,均对比不计入从众心理的系统动力学模型光伏装机意愿(仅由初始装机意愿决定)、计入从众心理的系统动力学模型和非系统动力学方法。在非动力学预测方法中,主流的是趋势分析类方法和神经网络法[20-22],其中神经网络法需训练模型的大量样本,不适于中长期预测,故选取趋势分析类中精度较高的二次自适应法[23]作比较。
4.2.1 1 年期预测结果
1 年期预测时,3 种方法获得的逐年预测结果如图4 所示所得结论如下。
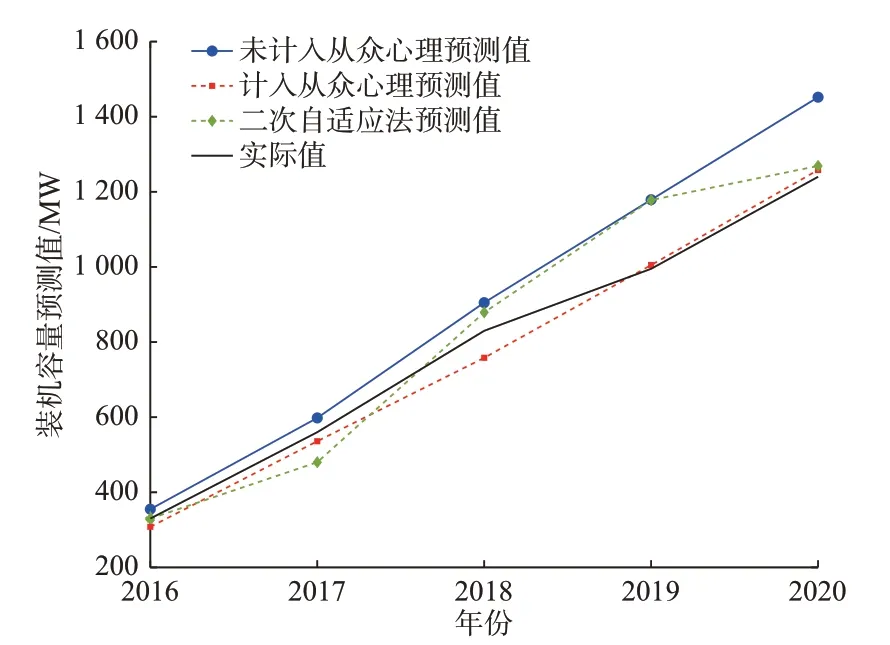
图4 3 种预测方法对A 市1 年期光伏预测结果对比Fig.4 Comparison of one-year photovoltaic forecasting results for city A with three forecasting methods
由图4 可得以下结论。
1)不计入从众心理时,装机意愿完全由投资回报率决定。第1 年预测结果高于计入从众心理的情况,也高于实际值;2017 年该市光伏政策调整,提升了光伏投资回报率(如图1 所示),当年光伏装机增速增大;2019 年该市光伏投资回报率下降,光伏装机增速也随之略有下降,但由于前期预测值过高,预测结果始终高于实际值。
2)二次自适应法不直接考虑光伏激励政策的影响,但会根据预测偏差调整二次指数平滑值,进而影响负荷预测的外推趋势。对于A 市,因初期利润低,基准年前后光伏装机增长缓慢,该法得到的2016、2017 年光伏装机预测值均低于实际值;此后,在自适应调整平滑系数的作用下,外推增长趋势加大,使得2018—2019 年预测值高于实际值;鉴于此,2020 年又下调了外推增速,预测值回落。可见,该法会使预测值在实际值上下浮动,变化趋势滞后明显,无法体现投资心理作用下光伏装机变化规律。
3)采用本文所提方法,2016—2018 年光伏装机容量显著低于不计入从众心理的情况,更接近实际值;2019 年政策调整使得投资回报率下降,但预测结果中光伏增速并未立即明显放缓,这也更符合实际情况。上述现象说明,计入从众心理影响的预测模型能够描述激励政策调节往往并不立即带来投资变化的现象。整体来看,本文所提方法5 年预测的绝对百分比误差均值为4.36%,比不计入从众心理的结果(11.80%)降低了7.44 个百分点,比二次自适应法(10.23%)降低了5.87 个百分点。
本文对中国B 市进行了同样的光伏装机容量预测分析(见附录B),得到了类似的结论,说明所提方法对其他地区也有一定的适用性。
4.2.2 5 年期预测结果
以2015 年为基准年,同样采用3 种方法进行5 年后的中长期预测,结果如图5 所示,可得如下结论:
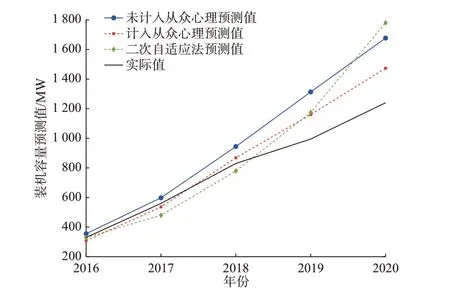
图5 3 种预测方法对A 市光伏5 年预测结果对比Fig.5 Comparison of five-year photovoltaic forecasting results of city A with three forecasting methods
1)由于5 年中该市光伏政策做了多次调整,而5 年期预测过程中一直延续基准年的光伏政策,没有计入政策的调整,故3 种方法下5 年期间的预测误差逐年增大。采用本文所提方法对2020 年预测结果的误差达到18.79%。
2)对不计入从众心理的系统动力学方法同样延续基准年的光伏政策,2020 年预测值的误差为35.24%;对趋势分析法延续2013—2015 年的趋势实施外推,不做平滑系数的逐年自适应修正,因该法不受地块饱和装机容量的限制,2020 年预测误差更大,达到43.55%。可见,本文所提方法通过计入从众心理,模拟出投资不立即随政策变化的特点,且增长趋势受地块饱和装机容量的限制,在中长期预测精度上仍有优势。
值得留意的是,采用本文所提方法对A 市2016—2020 年进行中长期预测的误差较大,是因为这5 年中该市光伏政策做了多次调整。随着光伏产业逐步成熟,政策将趋于稳定,政策稳定期采用本文方法所作中长期预测的精度会有所提升。
4.3 从众心理模型参数对预测效果的影响
本节通过摄动分析,考察从众心理模型中节点数N、初始关联节点数M、重连概率p对预测效果的影响。其中,N和M的取值决定了网络规模和个体间信息关联密度的大小[8],参数p决定了所生成网络的路径长度和聚类系数特征[14-15]。为保持小世界网络特征,本节分别对N和M的取值进行摄动,对p值进行联动,以保持网络平均路径长度和聚类系数的归一值不变[15]。
4.3.1 小世界网络规模(节点数N)的变化
节点数N取10、100、1 000 这3 种情况,保持M值不变,p值做联动变化,预测结果如附录C 所示。由附录C 可见:N从10 增加到100 时,预测值有较显著的偏差;但当N从100 增加到1 000 时,预测值几乎没有变化,这与文献[9]的结论相符。WS 模型是一个随机化的生成结果,其表现出来的统计学特征会随着节点数的增大而趋于稳定,N=100 时已能表现出稳定的统计学特征,在此基础上继续增大节点数,并不会改变预测结果但又会使计算效率降低。此外,总体来看,网络规模对预测结果的影响不是很大。
4.3.2 信息关联密度(参数M)的变化
保持网络规模N不变,将影响信息关联密度的M值在小世界网络典型取值2~4 的范围内摄动[8],预测结果如附录D 所示。由附录D 可知:M越大,光伏装机容量预测值增长得越快。这是因为,在同等网络规模下,M值越大,“某用户投资了光伏”的信息将被更多的关联节点获得,增大了投资信息在网络中的传播范围,使得从众投资决策概率增大,这对加快光伏装机容量增长有正向作用。不过,对比图4 和图5 可见,即便在M=4 的上限情况下,计入从众心理获得的预测精度仍高于不计入从众心理和采用二次自适应法的预测结果。对于一个实际地区,M的取值与地区风土人情有关,可取使得历史年预测最为精准的M值。
4.4 光伏不同发展阶段从众系数的选取
光伏产业发展的不同阶段,从众心理影响的程度是不同的[23],宜选取不同的从众系数τ。为此,本节对A 市光伏不同发展阶段摄动τ值(取0.3、0.5、0.7 和0.9),考察可获得最佳预测结果的τ值。
在 不 同 的 从 众 系 数τ下,A 市2016—2020 年 光伏预测结果见图6。
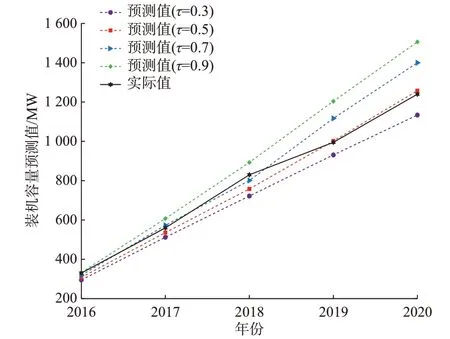
图6 不同从众系数取值下的光伏装机容量预测结果Fig.6 Forecasting results of photovoltaic installed capacity with different values of conformity coefficient
对比图1 可见,该市这些年经历了光伏产业的以下几个阶段,具有如下特征:
1)初创期(2015—2016 年):特征是成本高,回报率偏低。该阶段当从众系数取0.9 时,预测值与实际值最接近,百分比误差为0.91%。
2)成长期(2017—2018 年):成本下降使得回报率稳步上升,市场需求快速增长。此阶段从众系数下降到0.7 时预测效果最好,平均百分比误差为2.83%。这说明从众心理的影响有所弱化,使得2018 年投资回报率的小范围波动(从40.1%调整为46.1%)没有立即带来同样幅度新增装机容量。
3)成熟期(2018 年以后):投资增速放缓,产生从众心理衰退现象。该阶段获得最佳预测效果的从众系数的取值继续下降,为0.5。
上述规律表明,产业发展过程也是投资者对产业的认知逐步完善的过程,投资决策会从初期的盲目发展为后期的理性判断为主。实际应用时,一方面从众系数与地区光伏投资信息的传播途径、不同性格个体的组成等因素有关,需根据过往几年预测效果选取符合地区特点的值;另一方面也应结合地区光伏发展阶段,随着光伏产业趋于成熟而适当下调从众系数,由此可获得较佳预测效果。
5 结语
本文提出了一种计入从众心理对分布式光伏投资决策影响的系统动力学模型,适用于光伏装机容量的短期和中长期预测,预测结果表明:
1)本文方法与未计入从众心理影响及趋势外推的预测方法相比,可提高预测精度;
2)从众心理模型参数(节点数和关联节点数)在小世界网络典型范围内变化时,并不会改变所提方法在预测精度上的优越性;
3)随着光伏产业的发展,从众心理的影响逐步衰减。为此,可随地区光伏产业趋于成熟而适当下调从众系数,以获得较佳预测效果;
4)本文预测方法应用于不同城市的光伏预测均能取得提升预测精度的效果,但提升程度与预测期内地区光伏激励政策强度有关。
本文从从众心理角度为光伏装机发展与光伏投资回报率之间的非线性关系给出了一种合理的解释。由于中国光伏仍处于成熟期,本文算例主要关注于所提方法在光伏初创、成长和成熟期的适用性,其在光伏衰退期的适用性还有待检验。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。
