基于高维模型表达方法的新能源电力系统小干扰失稳风险评估

2022-07-26周一辰孙佳辉王书祥郝雅静

电力系统自动化 2022年14期

周一辰，孙佳辉，王书祥，郝雅静，刘铖

（1. 新能源电力系统国家重点实验室（华北电力大学），河北省保定市 071003；2. 现代电力系统仿真控制与绿色电能新技术教育部重点实验室（东北电力大学），吉林省吉林市 132012）

0 引言

受风光强不确定性与波动性影响，光伏、风电等新能源并网显著增加，导致电力系统源侧不确定程度升高。同时，电动汽车、分布式电源等快速增长，也导致负荷不确定性加强。源荷双侧多样化不确定因素加剧了系统运行状态的复杂多变性［1］。因此，新能源电力系统小干扰失稳风险评估尤为重要。

目前，电力系统不确定分析广泛采用的概率分析方法主要有模拟法、解析法和近似法［2-4］等。模拟法采用蒙特卡洛法进行模拟［5］，结果准确、程序简单，但是需要大量抽样，计算速度慢，更适用于算法检验。解析法如半不变量法［6］、近似法如点估计法［7］等，均要求输入变量相互独立，且仅针对正态分布随机变量时的误差较小，当不确定因素服从非正态分布时，计算精度变差，应用场景受限。近年来，以随机响应面方法（stochastic response surface method，SRSM）为代表的多项式混沌展开法研究取得快速发展。该方法利用正交多项式混沌展开之和表示输入-输出关系，适用于复杂非线性系统。文献［8］提出一种考虑实际不确定变量概率分布多峰特性的分段SRSM，提高了含非正态耦合随机变量的小干扰失稳风险评估精度，但是当输入变量个数较多时，采样成本过大易造成“维数灾”问题。现今新能源装机容量逐年增长，负荷变化特征日益突出，不确定性对电力系统小干扰稳定的影响不容忽视，如何准确、快速地评估大规模新能源、负荷接入的电力系统小干扰失稳风险，已成为亟须解决的问题。

近年来，高维模型表达（high-dimensional model representation，HDMR）方法在复杂不确定概率分析中的应用逐渐得到关注，在解决上述电力系统小干扰失稳风险问题上具有一定优势。HDMR 方法是一种描述非线性系统输入输出之间映射关系的分层表达方法［9］。根据稀疏效应原则［10］，通常物理系统中，只有输入变量的相对低阶相关性才会对输出产生较大影响。通过适当忽略对输出影响较小的高阶相关性，保留对输出影响较大的低阶相关性，HDMR 方法可以得到高维系统的低阶高精度表达，实现减少采样数量、提高建模效率的效果［11-12］。移动最小二乘（moving least squares，MLS）方法在最小二乘方法的基础上引入随变量“移动”而变化的权重，提高拟合精度，并使用种类丰富的基函数向量替换固定多项式，更适用于拟合特征多样化的复杂函数关系。

因此，为解决上述评估中的高效性和准确性难题，本文提出基于HDMR 方法的新能源电力系统小干扰失稳风险评估方法。首先，使用核密度估计法构建单变量概率分布模型，使用Pair-Copula 函数模型构建高维相关变量联合分布模型，刻画变量复杂概率特征。然后，提出基于MLS 方法和HDMR 方法（下文简称MLS-HDMR 方法）的新能源电力系统小干扰失稳风险评估方法，通过对非线性耦合相关性变量的稀疏逼近，降低采样数量、提高求解效率。并针对风-光-负荷实际概率分布特征，优化了采样方法并提高了评估准确性。最后，以新能源接入的2 区域4 机系统和新英格兰-纽约16 机系统为例进行算例分析，验证了本文所提方法的准确性和高效性。

1 风-光-负荷随机性建模

新能源电力系统中风电、光伏和负荷分布范围广、数量多、随机性强且存在多样化的复杂相关性，为准确评估新能源电力系统小干扰失稳风险，需对变量的随机性和相关性进行精准建模。本章首先分析了风-光-负荷随机分布特征，然后基于R 藤Pair-Copula 函数模型建立风-光-负荷多变量耦合相关模型。

1.1 风-光-负荷随机分布特征分析

1）概率分布特征

传统研究通常采用β分布、Weibull 分布、正态分布等概率分布函数描述风-光-负荷的随机性［13］，而光照、风速和负荷的实际概率分布函数各不相同，且解析表达式十分复杂，采用简单固定的标准分布函数建模，往往存在较大误差。以某地区为例，根据其光照、风速和负荷的四季某小时采样数据，分别建立实际概率分布模型（采用核密度估计法［14］）和标准分布模型（概率密度函数公式见附录A 式（A1）—式（A3）），得到如附录B 图B1—图B3 所示结果。可以看出实际情况下，实际概率分布呈现明显的多峰特征，而标准分布模型仅能体现单峰，难以准确刻画光照、风速和负荷的实际分布特征。

为准确刻画概率密度曲线的多峰分布特性，本文使用高斯核函数对随机变量xi（x=(xi)为风-光-负荷随机变量向量）的概率密度函数fpi(xi)进行估计:

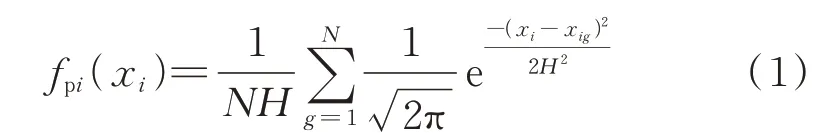
式中:N为历史数据的数量；H为窗宽；xig为xi的第g个样本。

2）耦合相关性

风-光-负荷多变量间存在耦合相关性，以某地区两风电场风速数据为例，绘制其散点图和频数分布直方图，得到如附录B 图B4 所示结果。可以看出，散点图中的点大部分集中在对角线上，这说明两风电场风速的耦合相关性极强，频数分布直方图在变量分布的上尾和下尾处取值较大，表明两风电场风速变量之间存在明显的尾部相关特征。采用线性相关系数ρp量度两风电场风速的线性相关性，Kendall 秩相关系数τ和Spearman 秩相关系数ρs来量度非线性相关性［15］，利用上尾相关系数λU和下尾相关系数λL来量度两风电场风速的尾部相关性（见附录C 式（C1）—式（C5）），计算得到如附录D 表D1所示结果。由表D1 可知，两风电场风速之间存在强非线性相关性，且存在对称的尾部相关性，与附录B图B4 分析结论一致。

综上可知，多变量间的复杂耦合相关性是随机建模中不可忽略的关键特征。为捕捉变量之间的这种线性、非线性和尾部相关关系，本文采用Pair-Copula 函数模型建立变量间的耦合相关性模型。

1.2 基于R 藤Pair-Copula 函数模型的多变量耦合相关性建模

式中:Cxi，vj|v-j(·)表示以条件分布函数F(xi|v-j)和F(vj|v-j)为变量的Copula 分布函数。

根据式（3）—式（5），可以将式（2）中的d维联合概率密度函数表示为多个二维Copula 密度函数及单个变量概率密度函数的乘积，这个过程称为Pair-Copula 构建（Pair-Copula construction，PPC）［16］。由此可知，建立合适的Copula 函数模型是准确建立多维变量联合概率密度函数的关键。当d＞2 时，不同变量两两组合会产生不同的Copula 函数模型，影响建立的联合概率密度函数的准确性。R 藤结构根据变量之间的最强相关性确定变量组合关系，具有较强的准确性和灵活性，本文使用R 藤实现上述PPC 过程，一个3 变量R 藤示例见附录E 式（E1）。

参考上述理论，基于R 藤Pair-Copula 函数模型的多变量耦合相关性建模的流程见附录B 图B5。首先，判断n个变量两两间相关性。文中采用附录C 式（C2）计算n个变量两两间的Kendall 秩相关系数τ。考虑负相关变量间的τ为负数，取τ的绝对值作判断变量，当|τ|大于阈值η（η＞0）时，认为变量间存在相关性。然后，基于得到的相关变量建立R 藤Pair-Copula 函数模型。若d≥2，使用式（2）—式（6）建立相关变量的R 藤Pair-Copula 函数模型，得到联合概率密度函数，其中当d=2 时，Pair-Copula函数模型变为单个二维Copula 函数模型。

综上可见，Pair-Copula 函数模型是多个二维Copula 函数模型的乘积，因此，Pair-Copula 函数模型的建模步骤和方法与二维Copula 函数模型相似，区别在于构建第t(t＞1)层Pair-Copula 函数模型时，变量变为如式（6）所示的条件分布。建模时，可使用极大似然估计法确定备选Copula 函数模型中的未知参数，其中与经验Copula 函数模型的欧氏距离最小者为最优Copula 函数模型。极大似然估计、经验Copula 函数模型和欧氏距离的公式见附录E式（E2）—式（E5）。

本文考虑6 种备选Copula 函数模型:正态-Copula、t-Copula、Clayton-Copula、Frank-Copula、Gumbel-Copula、SJC-Copula，这6 种Copula 函数模型能较全面地涵盖二维数据可能的联合概率分布，具体表达式及典型特征见附录F 表F1。以附录B图B4 中两组风速数据为例，建立相关性模型，并对其进行抽样［17］，得到如图B6 所示Copula 密度函数图和采样数据散点图，计算得到相关系数的数值见表F2。对比附录D 表D1 和附录F 表F2 可见，采样数据与原数据的相关系数接近，说明所建相关性模型可以较好地反映变量之间的相关性。

2 基于HDMR 方法的新能源电力系统小干扰概率稳定风险评估

2.1 新能源电力系统小干扰概率稳定问题

式中:Δz为系统状态变量增量；Aˉ(x)为新能源电力系统在运行点x处的状态矩阵。

受风速、辐照度和负荷的随机性影响，新能源电力系统小干扰稳定为概率事件。为评估新能源电力系统小干扰失稳风险，本文采用关键振荡模式阻尼比ξ表征新能源电力系统小干扰稳定状态，其与新能源电力系统中随机变量x的关系可用函数fξ表示。

式中:h(ξ)为关键振荡模式阻尼比的概率密度函数。

反之，该系统的小干扰失稳概率Pus=1-Ps。根据1.1 节分析可知，新能源电力系统中随机变量数量多且服从具有多峰特征的概率分布，不同随机变量间还存在复杂相关性，式（9）和式（10）的阻尼风险评估存在困难。

2.2 基于MLS-HDMR 方法的新能源系统小干扰失稳概率计算

为解决式（10）所示小干扰概率失稳风险评估问题，本节提出基于MLS-HDMR 方法的新能源系统小干扰失稳概率计算方法。假设式（7）所示的新能源电力系统中，代表随机性风速、辐照度、负荷的随机变量x的一个任意排序可以记作x=[x1，x2，…，xn]，那么根据HDMR 理论［21］，可以建立式（9）中关键振荡模式阻尼比ξ与输入随机变量x之间的HDMR 模型，表达式如下:

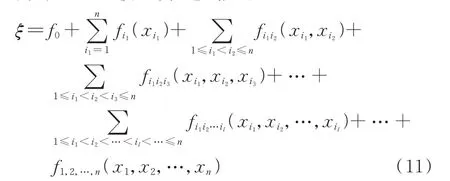
HDMR 模型通过不同阶数的分量函数对不同数目随机变量的耦合作用进行建模，具体地，式（11）中，f0为零阶分量，表示常数项；fi1(xi1)为一阶分量函数，表示单一变量xi1对输出的作用；fi1i2(xi1，xi2)为二阶分量函数，体现变量xi1、xi2相互耦合对输出的作用；fi1i2…il(xi1，xi2，…，xil)为l阶分量函数，体现l个变量相互耦合对输出的作用；f1，2，…，n(x1，x2，…，xn)为n阶分量函数，体现了所有变量耦合对输出的作用。

采用式（12）—式（17）能够计算各阶分量的精确值，但该计算过程基于模态分析逐阶分割出各阶分量的值，无法直接给出各阶分量函数的具体数学表示式。因此，本文采用MLS 方法来构建式（11）的各阶分量函数表达式，MLS 方法是一种高精度逼近方法［22-23］。

由MLS-HDMR 方法的求解过程可知，HDMR方法通过分层将原系统中变量的耦合关系分开表示，MLS 方法通过基函数可以区分变量的线性和非线性，因此通过判断系统中各变量是否存在耦合和非线性进行针对性建模，可以捕捉原系统稀疏性，降低采样数量，提高建模效率。该方法可直接用于拟合系统的输入-输出模型，使用拟合模型替换原系统模型，适用于随机变量为任意分布时的情况。因此，MLS-HDMR 方法对考虑实际变量分布的高维变量系统具有良好的适用性。

基于式（23）各阶分量表达式进行相加即可构成式（11），实现阻尼比ξ与随机变量x之间HDMR模型的构建。由于HDMR 模型为简单代数模型，将蒙特卡洛法应用于HDMR 模型，仅需微量代数计算，即可快速求解阻尼比ξ的概率密度函数h(ξ)。而进一步结合式（10），即可迅速计算得出新能源电力系统小干扰稳定和失稳的概率值。

3 新能源电力系统小干扰失稳风险评估过程及优化采样方案

根据第2 章的理论分析，本文所提新能源电力系统进行小干扰失稳风险评估的流程如图1 所示。分为准备阶段、模型构建、风险评估3 个部分，具体步骤如下:

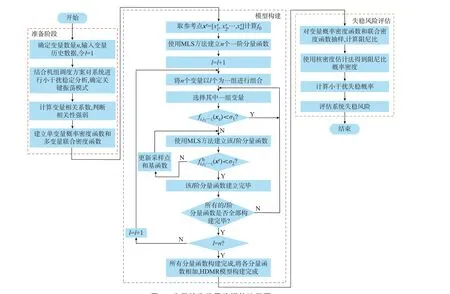
图1 小干扰失稳风险评估流程图Fig.1 Flow chart of risk assessment of small-signal instability

步骤1:准备阶段。根据风-光-负荷所构成的n个随机变量在待评估时间段内的历史数据，采用1.1节所述方法建立每个变量的概率密度函数；对于n个变量间复杂的相关性，采用1.2 节方法建立多变量高维联合密度函数。根据机组组合调度方案确定发电机在待评估时间段内的出力值，对系统进行小干扰稳定分析，选取弱阻尼模式作为关键振荡模式。

步骤3:风险评估。根据步骤1 所建立的多变量高维联合概率密度函数进行抽样，代入HDMR 模型计算阻尼比，采用核密度估计法构建阻尼比概率密度函数和累积分布函数，利用式（10）评估该时段内新能源电力系统小干扰失稳风险。

分析上述评估过程可以看出，在参考点和采样点附近，HDMR 模型精度相对较高。但是，由于实际变量存在多峰分布的概率特性，不同的采样点配置方案对评估精度存在影响，一般而言，选取高概率采样点集合将得到更准确的评估结果。基于此，本文进一步提出一种改进的参考点选取和采样点配置方法，可以在同样的采样成本下，提高HDMR 模型的各阶分量函数在高概率范围内的逼近精度，以提升风险评估精度。所提参考点及采样点选取方案如下。

在步骤2 中，建立l阶分量函数时，初始采样点选择l个变量最大、最小边界点，尽量使拟合函数包含边界信息，避免局部出现较大的拟合误差。当l阶分量函数精度不够需继续采样时，新增采样点取概率密度次高峰值处随机变量值。仅当峰值点已全部取为采样点但仍需继续采样时，新增采样点通过对变量概率密度函数进行随机采样获得。

4 算例分析

为验证多随机变量高维耦合复杂概率分布场景下，本文所提新能源电力系统小干扰失稳风险评估方法的准确性和高效性，本章以含3 个随机变量的IEEE 新英格兰2 区域4 机系统和含12 个随机变量的IEEE 16 机68 节点新英格兰-纽约互联系统为例进行验证分析。

4.1 4 机系统

算例采用如附录G 图G1 所示的IEEE 新英格兰2 区域4 机改进系统［24］，在母线1 接入光伏电站。考虑光伏电站的光照（x1）、负荷1（x2）和负荷2（x3）共3 个随机变量。发电机出力由机组组合调度方案确定，基础值取700 MW。光照数据取自NREL 实验室2011—2013 年连续3 年每年8 月中午11:00—12:00 的历史光照数据，负荷1 和2 的数据取自某两省同一时段的实际负荷数据。

对3 个随机变量的分布特性和相关性进行分析。在分布特性分析中，使用1.1 节所述方法建立光照和负荷的概率密度和分布曲线见附录G 图G2至图G4。由图可见，3 个随机变量的概率密度函数均明显存在多峰分布特征，难以采用正态分布等典型分布函数准确描述。在相关性分析中，通过附录C 式（C2）分别计算变量两两之间的Kendall 秩相关系数，其中光照和负荷之间的相关系数分别为0.04和0.03，相关性较弱，两负荷的相关系数为0.5，相关性较强。因此，需针对两负荷使用1.2 节所述方法建立联合概率密度模型。

基于R 藤Pair-Copula 函数模型计算得到的各备选Copula 函数模型的参数和欧氏距离见附录I 表I1。其中，Clayton-Copula 函数模型与经验Copula函数模型之间的欧氏距离，仅为其他4 种Copula 函数模型与经验Copula 函数模型之间欧氏距离的6.5%～17.3%，故选择Clayton-Copula 函数模型为最优Copula 函数模型。所得到的密度函数如图2 所示，从图2（b）和（c）对比可以看出，二者具有相同的相关特性，所使用的相关性建模方法完整刻画了原有数据的相关性特性，表明两负荷之间具有不对称的尾部相关性，且下尾相关性更强。

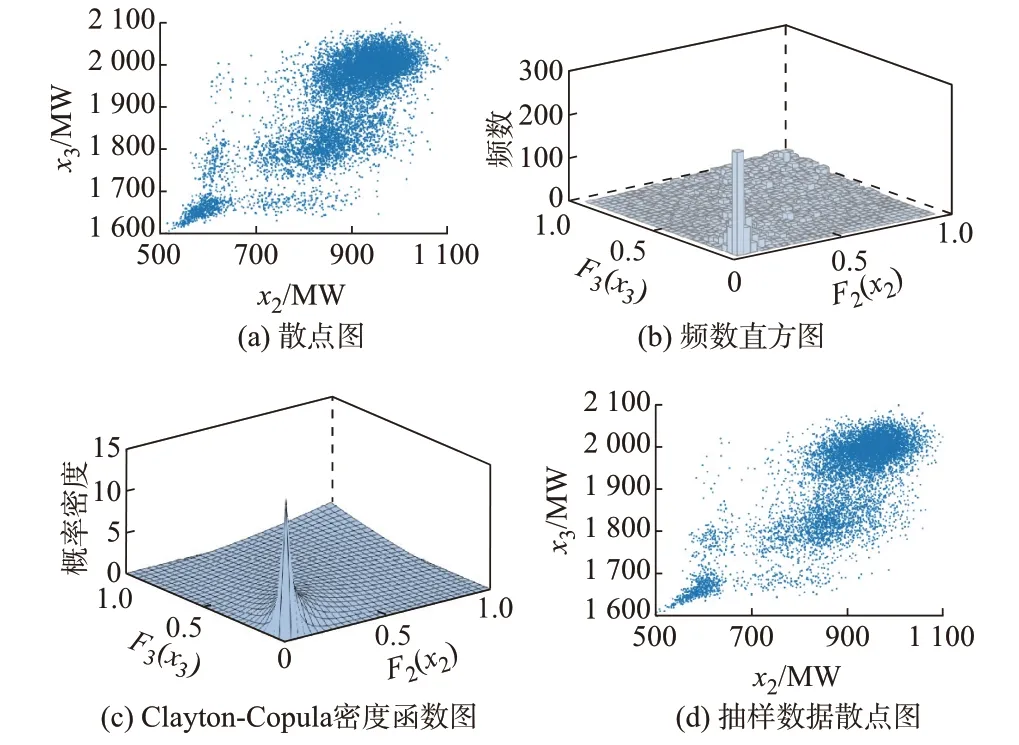
图2 Copula 函数模型的建模结果Fig.2 Modeling results of Copula function model

接下来确定关键振荡模式，取典型参数对系统进行模态分析，可以得出:系统中存在两个地区振荡模式，频率分别为1.05 Hz 和1.16 Hz，阻尼比分别为0.13 和0.08；一个区间振荡模式，频率为0.58 Hz，阻尼比为0.002。区间振荡模式阻尼比最小且处于弱阻尼状态。将此区间振荡模式阻尼比作为关键振荡模式阻尼比，采用前文所提方法建立HDMR 模型并评估该模式的失稳风险，得到阻尼比概率密度曲线与累积分布曲线如图3 所示。同时将优化采样的HDMR 方法与蒙特卡洛法、未优化的HDMR 方法、3 阶SRSM 和三点估计法作对比，将其他方法得到的区间模式阻尼比概率密度曲线与累积分布曲线一并展示在图3 中。

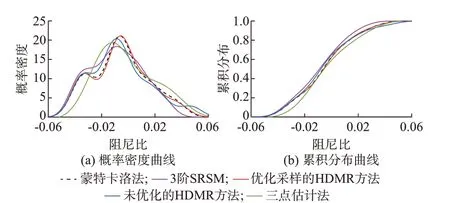
图3 阻尼比概率密度曲线与累积分布曲线（4 机系统）Fig.3 Probability density curves and cumulative distribution curves of damping ratio（4-machine system）

由图3（a）和（b）可以看出，本文所提优化采样的HDMR 方法评估出的概率密度和分布曲线与蒙特卡洛法求解的标准概率密度和分布曲线十分接近，这说明在多峰分布且具有强相关性情况下，本文所提优化采样的HDMR 方法在小干扰失稳风险评估方面具有高准确度。与未优化的HDMR 方法对比，所提方法准确性更好，所提出的基于概率分布的采样策略能提高对阻尼比概率模型的拟合精度。此外，HDMR 方法评估准确度整体上要显著优于SRSM 和三点估计法。这是因为本文所提HDMR方法能够直接处理变量多峰分布和复杂相关性并进行建模；而三点估计法仅在变量为正态分布时具备足够精度；SRSM 通过Nataf 变换实现相关非正态分布向独立标准正态分布变量的转换［8］，存在相关性的小幅转换误差。因此，在处理具有概率分布非正态、多峰及复杂相关性的电力系统小干扰失稳风险评估问题时，本文所提优化的HDMR 方法相比其他方法优势明显。

为进一步定量验证所提优化采样的HDMR 方法的模型准确度，根据变量概率密度进行了1 000 次抽样，分别使用蒙特卡洛法、未优化的HDMR 方法、优化采样的HDMR 方法和3 阶SRSM 计算相应的关键模式阻尼比，并进行对比分析。选取确定系数（用R2表示）、相对平均绝对误差（RAAE）、相对最大绝对误差（RMAE）这3 种指标，评价上述3 种方法拟合结果的准确度（指标计算公式见附录H 式（H1）—式（H3）），评价结果如表1 所示。其中，R2和RAAE 反映模型整体精度，RMAE 则能反映局部区域误差，R2越接近1，RAAE 和RMAE 越小，模型精度越高。

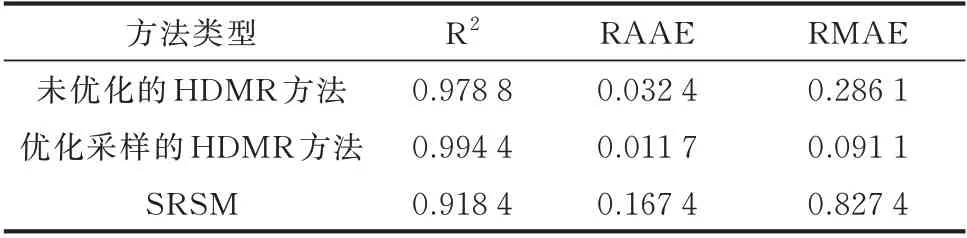
表1 评价指标Table 1 Evaluation indicators

由表1 可以看出，在整体精度方面，对于R2指标，SRSM 精度最低，未优化的HDMR 方法有明显提升，优化采样的HDMR 方法已超过0.99，整体误差极小。对于RAAE 指标，SRSM 分别是未优化的HDMR 方法和优化采样的HDMR 方法的16 倍和5 倍，这两点表明优化采样的HDMR 方法整体精度最高；同时，针对RMAE 指标，优化采样的HDMR方法也明显小于其他两个方法。可见，未优化的HDMR 方法的精度高于SRSM，并且，优化采样后的方法可以进一步提高HDMR 模型精度。

取阻尼比0.01 为该系统进行小干扰失稳风险失稳的阈值，即认为阻尼比小于0.01 时系统有失稳风险。使用上文提到的5 种方法计算得到的小干扰失稳概率分别为79%、79%、79%、81%、70%。HDMR 方法计算结果与蒙特卡洛法相同，优于SRSM，可以准确反映系统失稳风险。由于三点估计法不适用于复杂概率分布的失稳风险评估，存在显著误差，下文不再考虑使用。

4.2 16 机系统

算例基于改进的IEEE 16 机68 节点新英格兰-纽约互联［24］系统进行，系统图见附录G 图G5。设置1 个光照变量、4 个风速变量和7 个负荷变量，光伏接入55 节点，对应光照设为变量x′1，风机接入56、57、58 和59 节点，对应风速设为变量x′2至x′5，负荷接入3、13、16、20、21、23 和24 节点，对应负荷设为变量x′6至x′12。光照、风速和负荷数据为某地区2015—2017 年每年8 月中午11:00—12:00 的实测数据。

分析变量的随机性和相关性，首先建立变量的概率密度和分布曲线见附录G 图G6，3 种类型变量都呈现非标准分布，其中，光照和负荷变量有明显的多峰分布特征。然后，通过计算分析变量间Kendall秩相关系数（见表G1）可知，4 个风电场的风速两两之间的相关性较强，并且同光照之间存在负相关。构建风-光相关的R 藤Pair-Copula 函数模型，结果如附录I 表I2 所示。由表I2 可知，不同随机变量之间存在对称和非对称的尾部相关性，相关性关系十分复杂。

对系统进行模态分析，结果表明系统中存在4 个区域间振荡模式，其中区域1、2 和区域3、4、5 之间0.4 Hz 振荡模式的阻尼比最小，仅为0.004，取该振荡模式的阻尼比为关键振荡模式阻尼比，建立HDMR 模型评估系统小干扰失稳风险。

为验证本文方法的建模准确度，根据变量概率密度进行了1 000 次抽样，使用蒙特卡洛法、未优化的HDMR 方法和优化采样的HDMR 方法分别计算关键振荡模式阻尼比，得到的阻尼比概率密度和累积分布曲线如图4 所示。3 种方法计算得到的电力系统小干扰失稳概率均为23%，说明优化采样的HDMR 方法在高维情况下依然能够处理非标准分布且存在相关性的变量，可准确评估系统失稳风险。

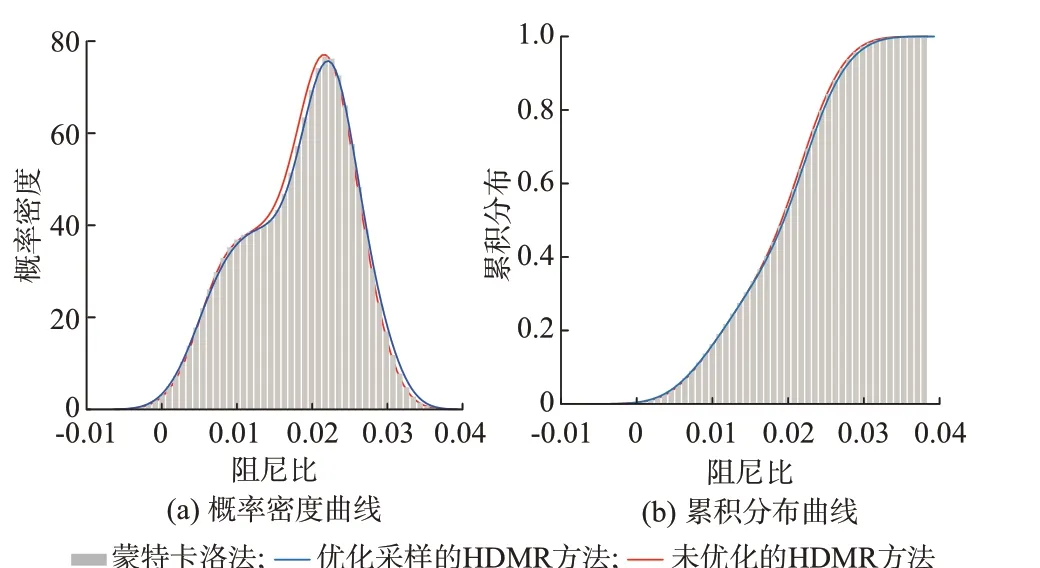
图4 阻尼比概率密度曲线与累积分布曲线(16 机系统)Fig.4 Probability density curves and cumulative distribution curves of damping ratio（16-machine system）

进一步分析本文方法进行风险评估的高效性，将HDMR 方法与SRSM 在模型建立和风险评估两个方面进行对比，HDMR 模型分量函数中变量的最高次数和SRSM 模型阶数均取3。表2 展示了两个算例中两种方法建模所需采样点数量，在低维变量下SRSM 采样点略高于HDMR 方法，但在高维变量下HDMR 方法所需采样点数远小于SRSM，可见变量数量越多，HDMR 方法采样优势明显。进一步分析表明，SRSM 两两变量间均存在耦合，在高维情况下会出现“维数灾”，与之相比，HDMR 方法只对系统中存在的非线性和低阶耦合项进行了建模，使用少量采样点即可得到精确的系统输出响应，有效提高了高维模型建模效率。

表2 算例采样点数Table 2 Numbers of sampling points for test systems

附录I 表I3 所示为16 机系统HDMR 方法建模时的采样点。可以观察到，HDMR 方法中不同一阶分量函数的采样点个数并不完全相同，说明HDMR方法捕捉到了各变量不同的线性和非线性，只有部分变量之间存在二阶分量函数，没有三阶及以上分量函数，即HDMR 方法只对系统中存在的低阶耦合项进行了建模，在保证精度的同时大大减少采样点数量。这说明电力系统存在稀疏效应，HDMR 方法应用于电力系统小干扰风险评估中可以发挥出更大优势。

本文方法运行于Intel Core i5-4590 CPU 电脑的MATLAB 平台，对文中改进16 机系统每一个采样点进行一次计算用时为0.7 s，HDMR 方法和SRSM 建模用时分别为38 s 和318 s，基于HDMR方法的风险评估与传统蒙特卡洛法风险评估所用时间分别为0.014 s 和721 s。可以看出，HDMR 方法在建模速度上优于SRSM，远小于蒙特卡洛法，可以快速完成电力系统小干扰失稳风险评估。综上所述，本文方法在建模和风险评估效率方面具有明显的优势。