考虑地理信息聚类分区的配电网多阶段动态规划方法

李争博，刘友波，任鹏哲，向 月，李秋燕，祁浩南

（1. 四川大学电气工程学院，四川省成都市 610065；2. 国网河南省电力公司经济技术研究院，河南省郑州市 450000）

0 引言

随着配电网负荷区域性增长的随机性和多样性不断提升，规模庞大、结构复杂的配电系统需要提出新的规划方法来优化当前规划方案的经济性与可行性［1］。多数配电网规划相关的研究开始利用负荷地理信息系统（geographic information system，GIS）和负荷预测数据挖掘负荷时空发展的潜在规律，并根据所挖掘出的负荷时空分布信息，开展配电网规划的相关工作。但是，目前基于GIS 展开的线路规划方法［2］主要应用于输电网络的线路规划。如文献［3］在输电线路规划时，利用双层运行优化模型和随机优化算法在地理信息图中确定输电走廊。然而，受限于网格划分颗粒度较粗且未能考虑配电网中背沟巷道、城市绿地等障碍区域的影响，此类方法难以确定规划线路在GIS 图中的实际走向和长度，规划结果的经济性和有效性存在进一步提升的空间。

随着配电网规划方面的研究不断深入，当前的变电站规划［4］、线路规划［5］以及分布式电源规划［6］问题均需要基于GIS 信息展开。如文献［7］根据负荷相似度在GIS 坐标系上对负荷进行分区处理，简化了问题规模，但该方法选用线路直线连接的方式容易造成规划结果偏离实际情况。文献［8］通过引入线路分布表示图来保证规划线路的辐射性，但受限于图形化方法的辐射性约束，无法针对存量电网展开进一步的规划。因此，可针对基于GIS 的图形化线路规划方法与基于待选路径集的网架动态规划算法同时进行改进。如文献［9］通过数据驱动的方法深度挖掘“投资方案-规划效益”的潜在联系，但其所挖掘的关联关系受到模拟输入样本的影响，准确性和普适性仍需进一步提升。文献［10］提出了基于增量最短路径的中压电缆网规划方法，但该方法规划的电缆路径簇并非区内全部路径集合，难以实现全局寻优。文献［9-10］分别从数学模型驱动和物理模型驱动两个角度对网架规划问题提出了求解方法，但规划结果仍存在优化的空间。

综上，考虑到负荷时空增长规律、规划线路长度变化和配电网网架多阶段动态发展模式给配电网规划带来的影响，本文提出了基于规划线路集和多阶段综合规划效益的配电网网架规划方法。该方法采用密度峰值聚类算法对负荷进行聚类分区，并以聚类中心作为等效负荷点绘制包含地理信息的GIS 网格图。随后，以各阶段等效负荷点的GIS 为基础，采用布雷森汉姆-粒子群优化（Bresenham-PSO）算法求解线路的空间分布，并据此计算出满足廊道约束和规划用地要求的规划线路长度集合。基于上述方法得到的线路长度和负荷预测数据，结合混合整数二阶锥规划（mixed-integer second-order cone programming，MISOCP）模型与动态规划（dynamic planning，DP）方法求解非凸非线性的配电网规划问题，实现规划方案经济性和可行性的提升。

1 考虑障碍区域影响的线路规划模型

传统配电网的线路规划在遇到穿过地理障碍区域的情况时，难以保证线路预留量［11］满足绕开障碍区域的要求，而预留量过大又会造成规划经济性降低。针对此类考虑空间信息的线路规划问题，GIS提供了负荷空间分布网格图；Bresenham 算法可确定两点相连所穿过的网格情况。基于以上两点可确定线路离散化表现形式。以网格内是否包含障碍区域为标准，可将各类网格赋予相应权重，找出节点相连所经过的网格，计算其环境权重平均值与直连线路长度的乘积作为待规划线路长度。再利用PSO算法求解线路规划模型得出规划线路集合，辅助解决线路的空间布线问题。

1.1 网格类型划分

在GIS 所提供的负荷空间分布图中，任意网格内部都包含地理因素、社会因素和经济因素等相关属性数据。根据各网格的属性数据对其进行相应的评级［12］，将网格分为以下3 类:

1）Ⅰ类网格:可任意穿越的网格，不额外引起线路增长或额外收取布线成本。

2）Ⅱ类网格:线路可穿越的网格，需考虑网格内的多种用地类型，按用地成本的不同设置相应的环境权重。

3）Ⅲ类网格:线路不可穿越的网格，需绕过此类网格进行规划。

1.2 基于Bresenham 算法构建的障碍区域线路长度模型

Bresenham 算法［13-14］是计算机图形学用来确定线段像素化、离散化的基本算法。该算法为适应显示器的像素化成像方式，可将网格图中的任意线段通过平移、翻转等操作变换为如附录A 图A1 所示的平缓线段。该线段沿x方向以0.5 格为递增梯度的方式检测线段间各点（如图中的点①②③④⑤⑥⑦⑧）与各网格的接触情况。若待检测点位于网格内部，如图中点②④⑦所示，则判断为点②④⑦所在的网格均为被穿过的网格。若待检测点位于两个网格的边界上，如图中点①③⑤所示，则判断为所接触的两个网格均被穿过。但是，若待检测点位于4 个网格的交界处，如图中点⑥⑧所示，则判断为该点未与周围4 个网格接触，周围4 个网格是否被穿过与此待检测点无关。

得到线段穿过的网格情况后，可根据所穿过的网格类型确定其环境权重ek，并根据式（1）计算出环境权重平均值作为该线段的环境系数E。把该系数与直连线段长度D的乘积作为考虑环境因素影响下的线路长度d，d即为任意两节点相连时的实际线路规划长度，其表达式为:

式中:ek为网格k的环境权重；Ng为线段所穿过的网格总数。

1.3 Bresenham-PSO 算法驱动的线路规划方法

尽管基于Bresenham 算法构建的障碍区域线路长度模型可以较为真实地计算出考虑环境因素影响下的线路长度，但该方法无法自动绕开不可穿越的Ⅲ类网格，降低了规划结果的可行性。因此，为了能够在含障碍区域的GIS 图中确定配电网线路空间分布，可将连续的线路进行离散化操作。即通过划分一条连续的线路为N段长度可变的子线段，各子线段通过分段点相连，并通过调整各个分段点位置来调整子线段在GIS 图中的分布。最后，离散化后的线路通过不断调整子线段的位置便能轻松地避开如Ⅲ类网格这样的不可规划区域。离散化的线路模型介绍如下:首先，将线段在网格图中经过平移翻转等操作变换为如附录A 图A2 所示的平缓线段，并将两点间的线段分为N个部分，插入N-1 个分割点，如图中的蓝点所示；然后，以各个分割点所在射线与水平方向的夹角θm作为输入量搭建线路规划模型，其中式（3）为目标函数，式（4）至式（7）为约束条件。

式中:dcom为环境因素影响下两点间规划的线路长度；dm为第m段分割线段长度，m=1，2，…，N；Δxm和Δym分别为第m-1 个分割点与第m个分割点之间横坐标差值和纵坐标差值；θm，min和θm，max分别为分割点m所在射线与水平轴夹角θm的最小值和最大值。

该问题本质上是一个连续、非线性、受约束的非凸问题，可采用PSO 算法对此类非线性问题进行求解。同时，由于输入变量θm的数量、可行空间与配电网网格划分的颗粒度及其信息的完备性、可用网格数目密切相关。故在背沟巷道和电缆管廊约束下的配电网规划求解过程中，通过不可规划的Ⅲ类网格对自变量θi的可行空间进行限制，极大程度减少了该问题可能出现的局部最优值。最后，为提高算法的速度与精度，该算法引入了自适应惯性权重公式如附录A 式（A1）所示。通过动态调整PSO 算法中的惯性因子，使得在粒子集中时，增大惯性权重值跳出局部寻优；在粒子分散时，减小惯性权重值逐渐向全局最优点靠近，以提高全局寻优能力。

2 基于规划路径集的网架规划凸模型

网架规划的物理模型［15］通常以最小化线路投资为目标函数，在安全运行约束的条件下确定网架结构。早期规划方案的目标函数对于成本的估算过于简单，忽略了随负荷增长而日益增加的线路损耗、线路运维等附加成本。同时，针对配电网规划的潮流约束而言，交流潮流方程式具有很强的非线性和非凸性，导致规划问题的优化求解难度较大。为解决以上问题，本文将基于现值因子计算的建设成本、损耗成本以及运维成本等综合成本作为模型的目标函数，改善规划结果的经济性。同时，将非凸、非线性的交流潮流方程进行二阶锥松弛、凸优化得到便于求解的凸模型，以降低网架规划的求解难度。最终，根据上述方法将传统网架规划模型优化为考虑线路综合规划成本的MISOCP 模型，降低了求解难度，提高了规划结果的经济性和可行性。

2.1 基于现值因子的综合规划成本分析

为获得更符合实际需求和长期规划效益的配电网规划方案，需以综合经济成本Ccom最低为目标，建立囊括线路建设成本Cline、线路维护CM和线路运行损耗Closs等综合成本的目标函数。表达式为:

式中:Φ为待规划线路集合；S为可选的电缆型号集合；lt为电缆型号t的单位长度成本；Zij，t为节点i、j之间 电 缆 型 号t的 线 路 电 缆 建 设 情 况，Zij，t=1 表 示 规划建设；dij为线路ij的长度。

2）线路维护成本

线路维护成本的年金现值随线路运行年数增加而有所变化，n年后线路维护成本需根据n年内的年利率进行转换计算得出。因此，假定每年维护成本A和年利率μ不变，n年内的总维护成本应按照“现值转年法”进行计算，以线路年维护成本与现值因子ω1的乘积作为各年线路维护成本现值之和，表达式为:

式中:iij为节点i、j之间线路的电流；Tmax为年最大负荷损耗小时数；λ为年均购电价格。

负荷增长会引起线路损耗逐年增加，线路运行损耗成本也随着损耗增加而逐年增长。假定峰值负荷的年增长率为σ，则线损电量的年增长率ξ=σ2+2σ，且n年内线路运行损耗所造成的总成本为第1 年的运行损耗成本与现值因子ω2的乘积。ω2的表达式为:

式中:Iij为节点i、j之间线路上电流的平方；rt为型号t的电缆单位长度电阻值。

2.2 凸优化的MISOCP 模型

为提高规划问题的求解效率与速度，传统网架规划模型须利用二阶锥松弛改进其非凸、非线性的交 流潮流方程［17-18］，得到凸优化的MISOCP 模型。改进后的模型需保证规划结果满足如下3 个方面的约束:网架辐射状结构约束、二阶锥松弛后的交流潮流约束以及节点电压和支路容量约束。由于约束公式较为繁多，此处不再赘述，具体内容参照附录A式（A2）至式（A17）所示。

3 配电网多阶段动态规划方法

配电网规划是一个中长期的动态规划过程，涉及多个对象、多类投资成本以及多个阶段的综合规划效益［19-20］。针对该类中长期规划问题的求解，配电网动态规划方法可将初始网架发展至饱和年的过程分为多个阶段，将一个长期规划问题分解为多个逐步递进的短期问题进行求解。但是，配电网动态规划方法可能会因划分阶段和负荷点数目过多产生“维数灾”问题。故该过程首先针对GIS 提供的各阶段负荷空间分布数据进行分析，通过基于密度峰值的快速聚类（clustering by fast search and find of density peak，CFSFDP）算法实现空间负荷聚类，并将聚类中心作为等效负荷点以缩小规划问题规模、提高求解效率。

3.1 基于CFSFDP 算法的空间负荷聚类

空间负荷预测（spatial load forecasting，SLF）是配电网规划的前期准备工作，现有SLF 方法［21］可根据GIS、历史负荷数据等在地理坐标轴上绘制出负荷空间分布网格图。文献［22-23］提出了利用元胞自动机原理、非参数核密度估计等进行未来多个阶段空间负荷预测的方法，可辅助本研究构建多阶段的负荷时空分布模型。但受到网格划分颗粒度的限制，部分负荷节点在GIS 网格图中的位置过于靠近，此类节点之间的线路优化不仅对于网格划分颗粒度的要求较高且优化结果的经济效益也不容乐观。故本文采用CFSFDP 算法按照负荷点的地理分布进行聚类分析，聚类中心的GIS 坐标可近似为环网柜或分支箱空间位置，将其绘制在GIS 网格图中作为等效负荷点。为确定等效负荷点在GIS 网格图中的空间分布，需先利用密度峰值算法计算出各负荷节点的局部密度ρi和相对距离δi如式（16）至式（18）所示。最后，筛选出局部密度与相对距离较大的负荷节点作为聚类中心绘制在GIS 网格图中，聚类中心和各负荷点关系展示如附录A 图A4 所示。

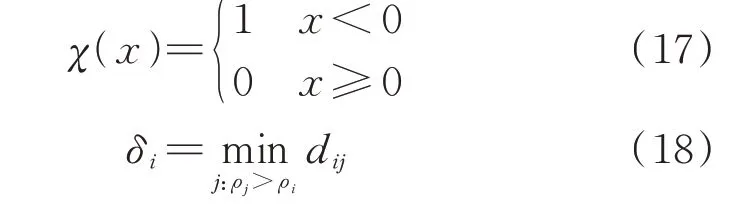
式中:dc为截断距离；χ(·)为逻辑判断函数。

3.2 配电网动态规划方法求解

基于GIS 负荷信息及聚类结果得到配电网初始网架信息、滚动年阶段性网架变化及饱和年规划的最终要求［24］。将该动态发展过程用图论的方法来描述，把各阶段的规划方案定义为该阶段的状态如附录A 图A5 所示，2 个状态之间的路线定义为状态转换的权值增量，找出一条权值增量最小的路线即为该问题的最优解。一般来说，配电网动态规划过程共分为n个阶段，每个阶段又可能会提供A-N个方案，临近两阶段间通过方案互相关联。任意阶段内规划方案的实现均需以实现上一阶段对应的规划方案为基础，该过程为单相传递、不可逆转。对于配电网规划而言，将各阶段间权值增量设置为相应方案的成本增量，从上述规划过程中找出一组滚动规划方案。该方案结果若能满足全阶段配电网规划综合成本最小，则为该规划问题的最优解。

中长期配电网规划过程中，一般规定5 年作为一个完整的配电网规划周期，按照DP 算法的要求将规划周期分成5 阶段，分别对应周期内的1 至5年。对应在MISOCP 模型中的修改，即为按照待规划周期数设置网架拓扑对应的二进制变量Zn ij（n取1至5）。另外，为按照上述DP 算法展开网架结构的扩展规划，需在MISOCP 模型的约束中进行调整，具体修改内容如附录A 式（A18）至式（A21）所示。

4 算例分析

通过仿真某待规划城区配电系统的规划流程对该方法进行验证。选取该系统内某一供电单元展开规划，自建设基准年开始设置为期5 年的规划周期，第5 年作为规划饱和年。配电系统内变电站、负荷点的分布信息利用GIS 获取，并在网格坐标图上绘制出相应的位置。网架规划中待选导线类型及其余参数信息如附录B 表B1 和表B2 所示。

4.1 规划线路长度计算

根据第1 章线路规划要求，将该区域地理图像划分为160×160 的网格图如附录B 图B1 所示。按照CFSFDP 算法将各规划阶段的负荷预测结果进行空间位置聚类，得到各阶段等效负荷点分布情况，用不同颜色将各阶段负荷点区分开来。根据各网格所包含的地理信息，规定该图内电缆沟覆盖的网格为Ⅰ类网格，该类网格环境权重设置为1；内部情况复杂且包含多种不同用地情况的网格设置为Ⅱ类网格，考虑到直埋电缆或新建电缆管廊均会引起成本增加需提高相应环境系数，其环境权重设置为2～4；建筑物、绿地覆盖的网格区域为不可穿过的Ⅲ类网格，其环境权重取极大值。

根据1.3 节所提及的线路离散化操作可知，为确定上述160×160 的网格图内各负荷节点间规划线路的环境系数，需要调整规划线路分段情况，选取出该网格划分颗粒度下环境系数最小、求解效率最高的分段数N作为最佳分段数。由于分段数N的增加，会引起拐点的数目增多和计算难度的增加，降低了经济效益与求解效率［25］。因此，图1 中展示了不同分段数下，粒子群算法迭代计算的最终结果。由图可知，不同分段数下该算法最终所求得规划线路结果的网格类型数目存在差异。而随着分段数N的增加，规划线路的灵活性得到了提升，Ⅰ类网格数目增加、Ⅱ类网格数目下降。但在图1 中，当分段数增大到6 段以上时，规划线路的环境系数总和基本保持稳定，Ⅱ类网格数目也趋于最小值。所以，为降低求解时间和求解难度，选取N=6 时的计算结果作为后续规划中待规划线路的长度。

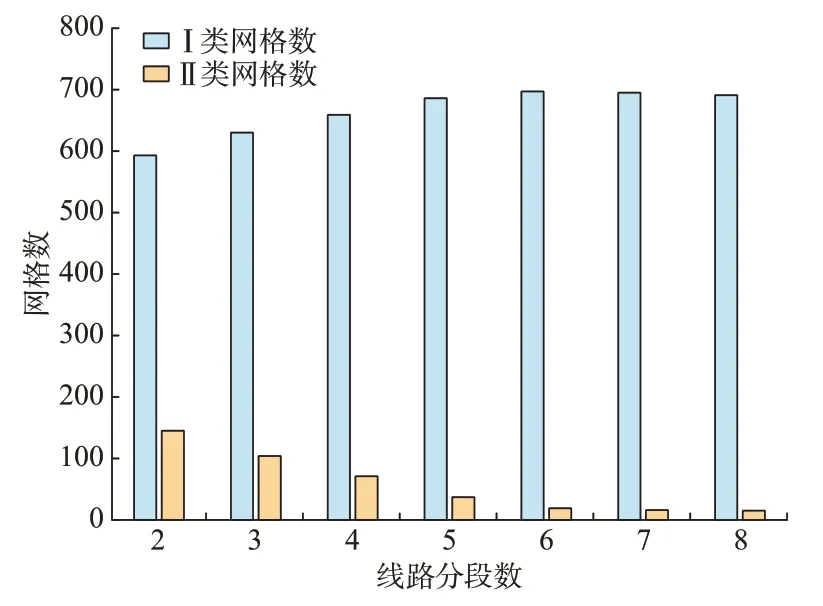
图1 不同分段数下规划线路网格数量对比Fig.1 Comparison of number of planned route grids with different number of segments

4.2 实际算例分析

将待预测区域发展阶段的空间负荷预测情况按时间进行划分，并把为期5 年的规划周期分为5 个阶段。对各个阶段负荷点展开空间上的密度峰值聚类分析，由图2 可知，各阶段聚类结果中约7 个点的局部密度ρ和相对距离δ都远大于其他数据点。因而，选取这类负荷点作为聚类中心代表等效负荷点，各阶段新增等效负荷点的空间分布以及各阶段负荷总容量展示如附录B 图B1 和表B3 所示。

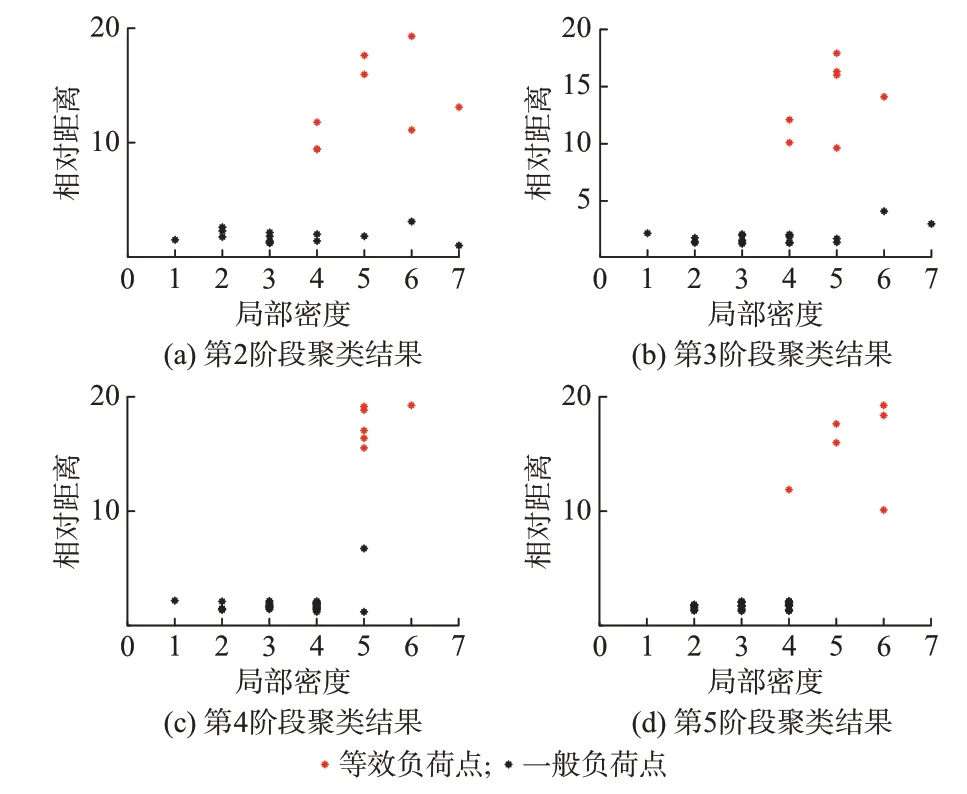
图2 负荷空间聚类决策图Fig.2 Decision graph of load spatial clustering

基于附录B 图B1 中当前阶段电源及等效负荷点的空间分布展开后续4 个阶段的网架规划，并按照图2 聚类结果设置各阶段等效负荷点的峰值负荷，基于负荷预测结果作为边界条件，计算出各阶段规划方案中网架结构对应的二进制变量Zn ij，并计算现值因子影响下各阶段的综合规划成本，将该方法的计算结果与贪心算法计算出的规划成本在表1 中进行对比。由表1 可知，虽在第2、3 阶段基于贪心算法展开的规划方案建设成本更低，经济效益更好，但在第4、5 阶段时，贪心算法规划结果的建设成本与运维成本均高于DP 算法。统筹计算第1至5 阶段总规划成本可知，DP 算法规划结果综合成本为1 053 万元，而贪心算法规划结果综合成本为1 123 万元。故为在满足负荷供电需求的同时节约整体的规划成本，需采用DP 算法统筹全局的建设成本以及全周期的运维成本，合理分配各阶段所需的规划成本达到全周期规划效益最大的目的。最后，上述两种方法规划结果所对应的网架结构对比见图B2。线路电缆类型及线路电流见图B3。

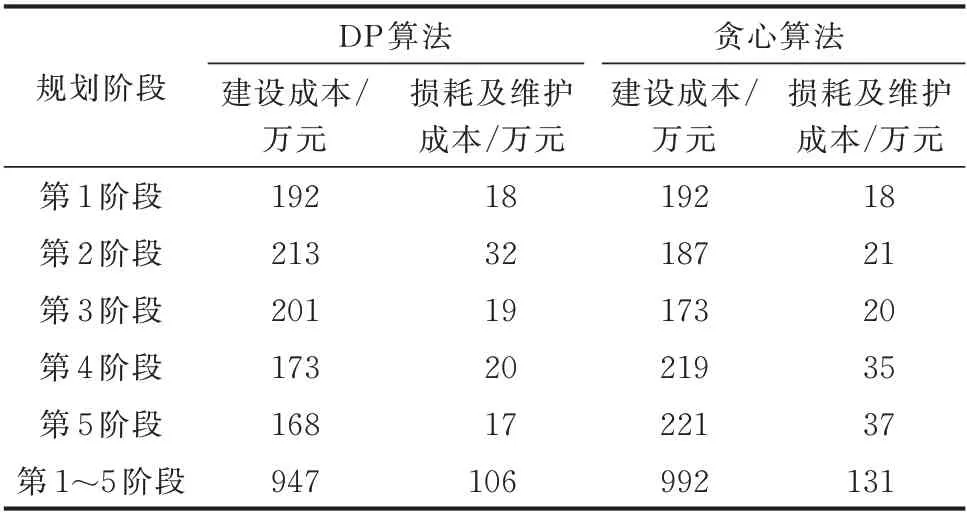
表1 各阶段规划成本Table 1 Planning cost at each stage

4.3 求解方法性能评估

文献［10］介绍了一种基于增量最短路径法的全电缆中压配电网规划方法。该算法在城市配电网电缆线路规划方面确实能够起到一定的优化作用，但该方法难以找到规划问题的全局最优解。而凸优化后的MISOCP 模型却能够完成该类问题的全局寻优，快速找出满足规划需求的最优方案。故以文献［10］算例数据为依据，针对MISOCP 模型与最短路径法的规划结果进行分析。由图3 可知，在无GIS（即按照欧氏距离计算线路长度）的条件下，本文所提方法虽在总规划成本上略高于增量最短路径法所求结果，但建设和损耗成本相差无几，表明所提方法可辅助寻找全局最优解，具有较强的通用性。然而，按照GIS 计算线路长度时，增量最短路径法受到障碍区域影响，规划成本大幅提升。而结合了DP 算法的MISOCP 模型能够避免前期阶段贪心策略的干扰，快速遍历基于GIS 约束的可行空间，节省了配电网规划的综合成本。

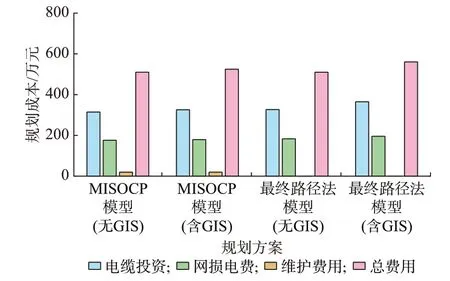
图3 不同规划方案成本对比Fig.3 Comparison of costs with different planning schemes

最后，采用上述数据按照基于DP 算法和基于枚举法的MISOCP 模型分别进行求解，结果如表2所示。

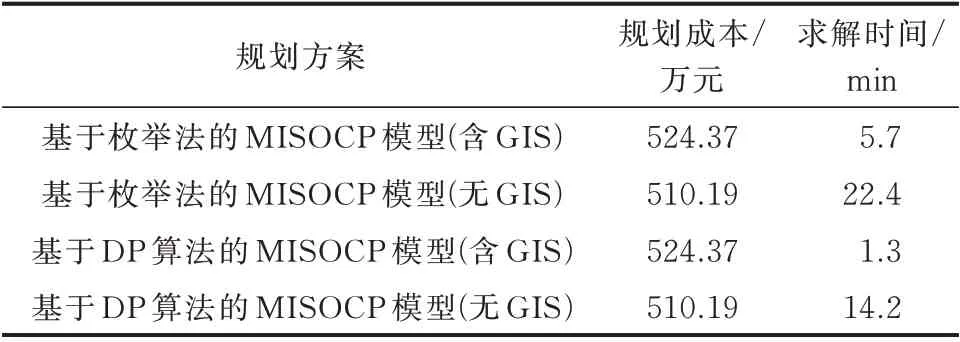
表2 不同规划方案下结果对比Table 2 Comparison of results with different planning schemes

由表2 可知，若是利用GIS 加以约束，无论是枚举法还是动态规划方法，二者的求解时间均未超过30 min，且采用DP 算法进行求解较枚举法而言能够进一步优化配电网规划问题的可行空间，从而进一步缩短求解时间，使得求解速度满足规划需求。

最后，MISOCP 模型在规划过程中充分考虑馈线规划的全周期综合成本，较之增量最短路径法进一步精细化了建设成本、损耗成本及运维成本3 个方面的计算，更符合实际应用的需求。

5 结语

在考虑障碍区域影响和多阶段综合规划效益的基础上，提出了一种基于GIS 的多阶段动态规划方法，用于辅助配电网待规划线路长度计算和提高规划方案的经济效益。通过算例分析，得到如下结论:

1）在配电网网格化地理信息图中，线路规划方法能绕开障碍区域解决供电线路布线问题，通过Bresenham 算法可得到精确的线路长度和规划线路的空间布局，有利于提高方案经济性、可行性。

2）采用基于现值因子计算的综合规划成本可辅助决策各条线路型号选型，配电网规划MISOCP模型及其凸优化计算效率高、结果稳定，适合含有多线路、多阶段约束的配电网规划决策，提升滚动周期内配电网可开放容量。

3）考虑配电网综合规划成本的多阶段DP 方法，能够充分满足负荷阶段性增长引起的网架结构性调整需求，提供建设、运维、损耗等多方面的精准评估，符合实际配电网中长期规划建设特性，具有一定的通用性。

虽然所提方法能够完成配电网网架结构的全周期规划。但是，目前规划目标已远不止辐射状电网一种，若将整个规划周期进行多次划分，则随着划分的阶段数不断增加，后续阶段产生的规划场景将会呈指数形式增长，动态规划将面临“维数灾”问题。该网架DP 方法虽能完成配电网系统的扩张规划，但由于城市发展中仍旧存在拆迁或绿地改造引起的负荷点移除和负荷需求下降的情况，故后续研究中还需要对模型方法进行相应的调整改进。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。