基于不确定性最优潮流的配电网分布式发电消纳能力评估

朱俊澎，黄 勇，马 良，李红军，袁 越

（1. 河海大学能源与电气学院，江苏省南京市 211100；2. 国网经济技术研究院有限公司，北京市 102209）

0 引言

近年来，可再生能源装机容量稳步提升［1-2］，提高清洁能源在能源结构中的占比已经成为广泛共识。随着建设新型电力系统目标的提出，以光伏发电为主的可再生分布式发电（renewable distributed generation，RDG）接入配电网已成为能源转型的重要途径之一。然而，随着渗透率的逐步提高，部分地区的配电网已出现对于新能源消纳能力不足的情况。准确客观地评估新能源在配电网中的消纳能力已成为主动配电网和新能源在规划和运行中的重要问题之一［3］。

评估新能源消纳能力的方法从潮流形式上可分为非潮流优化类方法和基于最优潮流（optimal power flow，OPF）的方法。前者基于仿真计算［4-5］和生产模拟［6-8］等手段，测算电力系统对于新能源的消纳能力。相比之下，更多的研究采用了基于OPF 的新能源消纳评估模型［9-16］。文献［11］建立了同时考虑OPF 和时序生产模拟的消纳能力评估方法。文献［12］建立了基于电力和燃气系统联合优化的消纳能力评估模型。已有文献在消纳能力评估OPF模型中考虑了新能源出力的不确定性。典型不确定性OPF 建模和分析方法包括鲁棒优化［13-14］和随机优化［15-16］。在电力系统中，直接基于新能源注入功率的概率分布对电压和支路功率等状态量的概率分布进行分析难度较大，关于通过直接求解随机OPF模型进行新能源消纳能力分析的研究尚未见报道。文献［15］建立了考虑时空相关性的光伏出力概率模型及相应的消纳能力评估模型。文献［16］考虑了消纳能力评估模型中RDG 出力的概率特性，通过蒙特卡洛仿真得到场景集合，从而将不确定性优化问题转化为确定性OPF 模型。此外，通过场景抽样将随机优化转化为确定性优化问题的思路也开始应用于RDG 和主动配电网的联合规划问题［17-18］。就随机OPF 问题而言，已有学者提出了基于点估计法［19-20］、一次二阶矩法［21］、半不变量法［22］的分析求解方法。其中，点估计法基于少量场景的选取进行分析，难以体现随机环境的全部信息，无法得到状态量的概率分布；一次二阶矩法同样为近似方法，仅关注均值和标准差特征，算法模型误差较大［23］；半不变量法为解析方法，基于线性模型建立环境量与状态量的各阶半不变量之间的映射关系，从而对状态量的各阶矩进行计算。然而，其精度仍存在一定的争议，无法得到状态量概率分布的严格解析表达式，且不便于对状态量随机特征与各环境量之间的深层关系进行机理分析。

针对以上问题，本文提出一种新型的配电网不确定潮流分析思路。首先，证明了配电网中注入功率不确定量到节点电压幅值、支路功率波动量之间的映射关系；其次，建立了当注入功率不确定性用概率或仿射描述时，电压幅值、支路功率不确定性的解析表达式，定量分析了状态量的不确定特征与各节点注入量不确定特征之间的关系机理。在以上不确定性潮流分析的基础上，进一步提出了配电网中RDG 消纳能力评估的不确定性OPF 模型，建立了模型的等价转换和求解方法。

本文的创新性及主要贡献如下:

1）论证并建立了系统状态波动量与注入波动量之间的显式函数关系，为不确定性潮流分析提供了新的理论依据，并依此提出了相应的概率及仿射潮流分析方法。

2）提出的概率潮流分析方法可以克服现有方法中通过求各阶矩或半不变量近似代替求解概率分布而导致的概率分布描述不精确的弊端，可在解析层面实现从注入量到状态量的完整映射。提出的仿射潮流避免了仿射算术中固有的保守性，从而得到更为精确的状态量波动区间。

3）基于所提出的不确定性潮流分析方法进一步建立了配电网分布式电源消纳能力评估模型，提出了可再生能源功率不确定性用概率或仿射描述时消纳能力评估模型的确定性等价转换方法。

1 不确定性潮流分析

本章分析的潮流基础为辐射状配电网的线性化DistFlow。在辐射状配电网中，以变电站节点作为根节点，任意节点j有唯一的父节点。当节点j不是末端节点时，可能有一个或多个子节点，其子节点集合记为w（j）。辐射状配电网的线性化DistFlow 可表示为:

基于上述配电网潮流模型，本文提出并证明以下定理和推论。

定理1:当某节点有功和无功注入功率发生不确定性波动时，系统中任意节点电压幅值平方项随之产生的波动量为上述有功和无功注入功率波动量的线性组合。

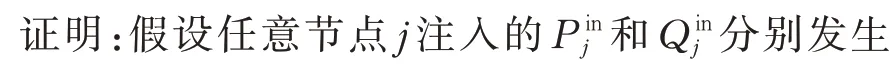
图1 不确定性潮流示意图Fig.1 Schematic diagram of uncertain power flow

基于以上证明过程和结果可以得到如下推论。

推论1:当存在多个节点有功和无功注入功率发生不确定性波动时，系统中任意节点电压平方项随之产生的波动量为上述注入功率波动量的线性组合。

同理，当存在多个节点有功和无功注入功率发生不确定性波动时，任意支路功率随之产生的波动量也表现出线性相关性，不再赘述。

2 注入功率仿射和概率表示下的不确定性潮流

本章建立注入功率不确定性在不同数学描述方式下的节点电压、支路功率等状态量的分析方法。由于支路的有功和无功功率在形式上完全一致且互相解耦。因此，为简化描述，本章中关于支路功率建模的部分仅以有功功率为例进行分析。

2.1 仿射潮流分析

当注入功率的不确定性用式（13）和式（14）所示的仿射形式表示时，根据推论1 和推论2，节点电压和支路功率的解析表达式分别如式（15）和式（16）所示。

2.2 概率潮流分析

当用概率表示时，注入功率可以表示为一个确定量与一个随机量之和，表达式为:

式中:N(·)为正态分布函数；σk为节点k有功功率的标准差。

在此情况下，基于式（23）和式（24）可以将状态变量的不确定性约束转化为一定概率意义下的确定性约束，从而对不确定性OPF 进行等价转化。

3 基于不确定性OPF 的RDG 消纳评估基础模型

基于上述不确定性潮流分析，本章进一步考虑RDG 的无功调节能力，提出基于不确定性OPF 的RDG 消纳评估基础模型，表达式为:

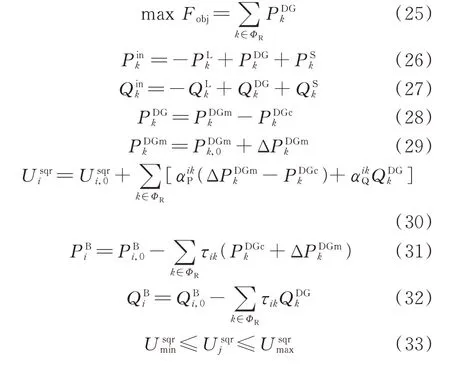
在数学形式上，式（25）—式（36）所描述的消纳能力评估模型为含有随机变量的二阶锥规划模型。其中，式（26）和式（27）为节点注入功率表达式；式（28）和式（29）分别为RDG 的有功出力同时受到含有不确定性的有功出力预测值及切机量约束；式（30）为节点电压表达式；式（31）和式（32）分别为支路有功和无功功率表达式；式（33）为电压幅值约束；式（34）为RDG 出力约束，可采用正方形约束进行线性化［25］；式（35）和式（36）为支路传输功率约束。

1）当RDG 有功功率预测值PDGmk采用仿射形式描述时，式（30）和式（31）分别等价转化为:

式 中:α为参数，1-α为 置 信水平；FN(·)、x0和σ分别为式（43）和式（44）描述的正态分布的概率分布函数、期望值和标准差。

具体地，1-α为不出现状态量越限的概率，反映了概率意义下的可消纳水平，体现了在概率描述下对于消纳原则的定义。

经过上述转化，无论注入功率的不确定性采用仿射或概率描述，转化后的模型在数学形式上均为线性规划模型，可方便地求得全局最优解。

4 算例分析

4.1 参数设置

以安徽省金寨县某110 kV 变电站的2 条10 kV馈线为例进行算例分析。系统的网络结构和RDG的接入位置如附录A 图A1 所示。馈线参数见附录A 表A1；典型负荷数据见附录A 表A2。RDG 容量参数见附录A 表A3。

4.2 线性化DistFlow 潮流误差分析

首先对本文建模的基础，即线性化DistFlow 求解潮流的精确性进行分析。选取不接入RDG 和RDG 有功出力为0.5 p.u.这2 种情况，对比基于线性化DistFlow 和精确潮流求解的结果，如附录A 图A2 所示。由图A2 可知，即便考虑高渗透率分布式电源接入下的功率倒送场景，线性潮流计算电压幅值的误差均未超过0.001 5；完全满足配电系统运行分析的精度需求。支路功率方面，平均支路功率偏差百分比为0.3%，最大支路有功、无功功率偏差分别为18.4 kW 和15.0 kvar，对于支路功率约束的影响亦可以忽略不计。

4.3 不确定性潮流分析验证

以馈线1 为例考虑单一节点有功功率注入的不确定性，对电压分布进行理论计算和仿真，以验证不确定性潮流分析的正确性。当设置节点19 注入不确定性功率时，基于有功影响因子的定义，可将馈线1 分为若干子集。节点集合A={2，15}，节点集合B={5，16，17}、节点集合C={6，18}、节点集合D={9，10，11，12，13，14}、节点集合E={19，20，21}、节点集合F={1，2，3，4，5，6，7，8，9，19}。节点集合A至E内各元素与节点19 之间的有功电压影响因子是相同的，在基值系统选取为容量SN=10 MW，电压UN=10 kV 时，根据式（11）计算得到有功电压影响 因 子 分 别 为0.092 4、0.343 0、0.417 0、0.657 0、0.730 0。节点集合F中，随着节点编号的增大，与节点19 之间的有功影响因子递增。

1）不确定性功率用仿射表示

根据Jarque-Bera 正态分布检验，各节点电压平方的分布均满足正态分布假设，初步验证了理论分析的正确性。进一步，以节点2、5、9、19 为例，节点电压平方的频数分布直方图和正态分布概率密度曲线如附录A 图A3 所示。基于式（23）理论计算得到的上述各节点电压平方项均值和标准差以及相应的仿真结果见附录A 表A4，仿真数据进一步验证了理论分析的正确性。需要说明的是，图2 和图3 中电压波动的幅度并不相同，这是因为仿射或区间对于不确定量的描述是有界的，而正态分布等概率描述是无界的，包含了对不确定量的尾部建模，即兼顾了小概率事件的发生。同时，注入量采用随机和仿射不同描述形式下系统状态量的不确定性具有一定的内在联系，结合本节算例分析，节点19 的注入功率在仿射描述下取值范围对应了概率描述下期望值波动1 个标准差的区间，而根据仿射潮流和概率潮流的求解结果可知，仿射潮流中节点电压和支路潮流波动范围亦对应了概率潮流中相应状态量在期望值波动1 个标准差的波动区间，体现了仿射和概率潮流在理论原理上的一致性。

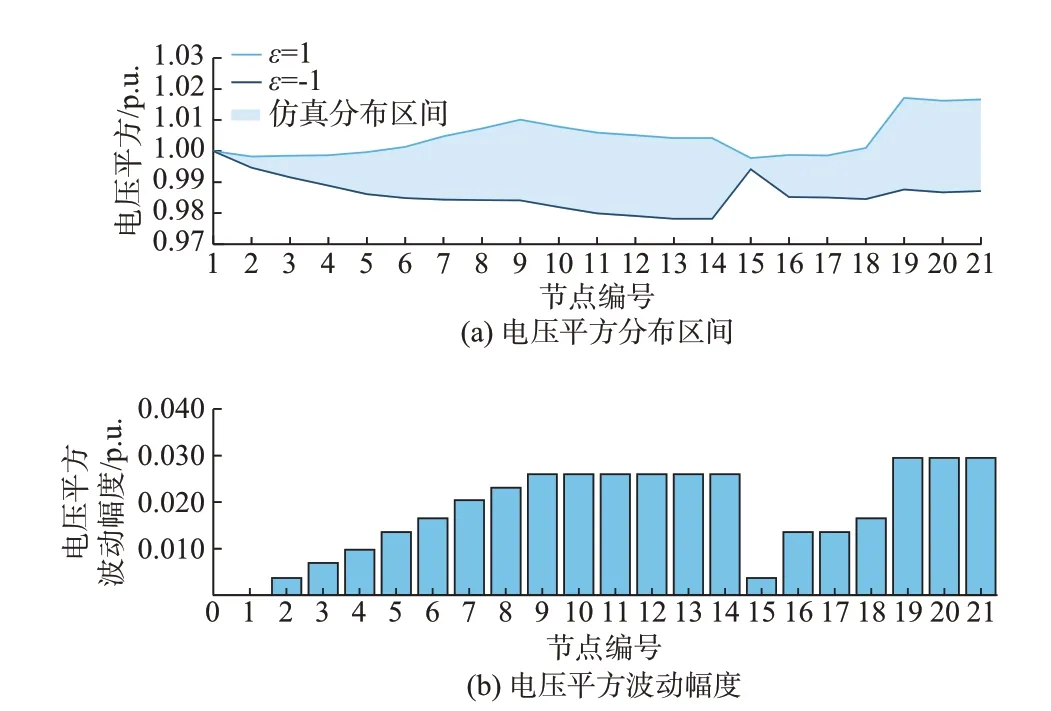
图2 节点电压平方的分布和波动幅度Fig.2 Distribution and fluctuation magnitude of node voltage square

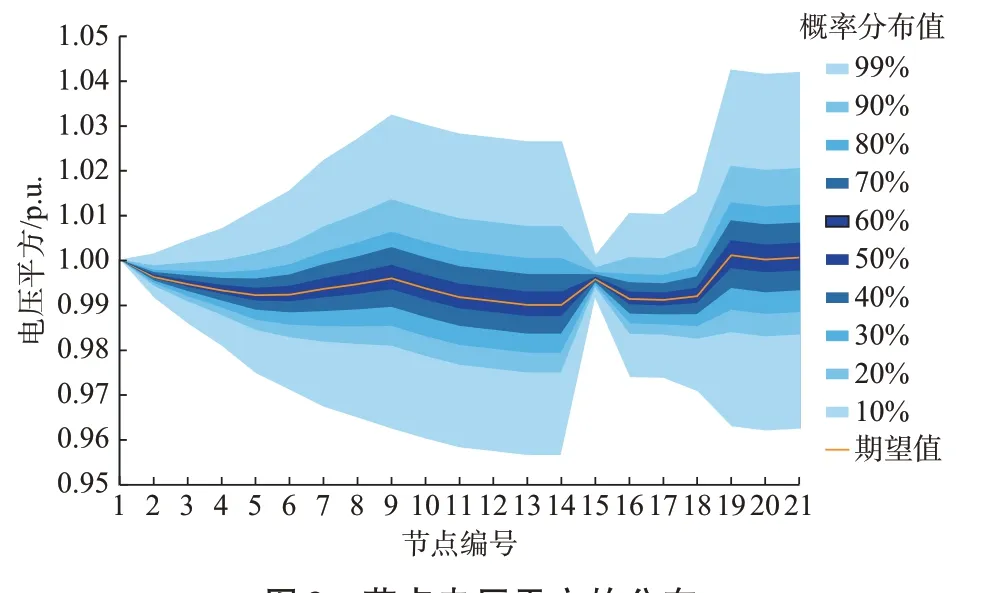
图3 节点电压平方的分布Fig.3 Distribution of node voltage square

4.4 消纳能力分析验证

以概率建模方式为例，对基于不确定潮流分析的RDG 消纳能力评估模型进行验证。各RDG 最大有功出力满足N（PDGm，uPDGm）的独立正态分布，其中PDGm为最大有功功率的预测值，算例参数设置为装机容量的80%；μ为预测精度系数，分别测试0%、5.0%、7.5%和10.0%等不同取值。式（49）中，1-α分别选取90%、92%、94%及98%等不同取值，代表不同概率意义下的消纳原则。不同预测精度及消纳原则下，RDG 的最大消纳功率如附录A 表A5 所示。由表A5 可知，一方面，随着预测精度的提升，RDG 最大消纳能力也相应得到提升；另一方面，消纳原则越苛刻，则运行结果更为保守，相应的消纳水平越低。算例表明，电压约束为限制RDG 消纳的主要约束。

具体地，以1-α=90%消纳标准为例，不同预测精度μ取值下节点电压平方的均值和波动情况如图4 所示，其中虚线表示电压幅值平方的上限。图4中，由于选取了同样的消纳原则，各子图中电压越限的概率是一致的，而预测精度的不同导致了随机性波动的幅度不同。一方面，随着不确定性增大，为了实现相同的消纳原则，电压的期望值需要更为保守；另一方面，同样选取7.5%的预测误差，在不同1-α取值下，电压平方项的分布如图5 所示。

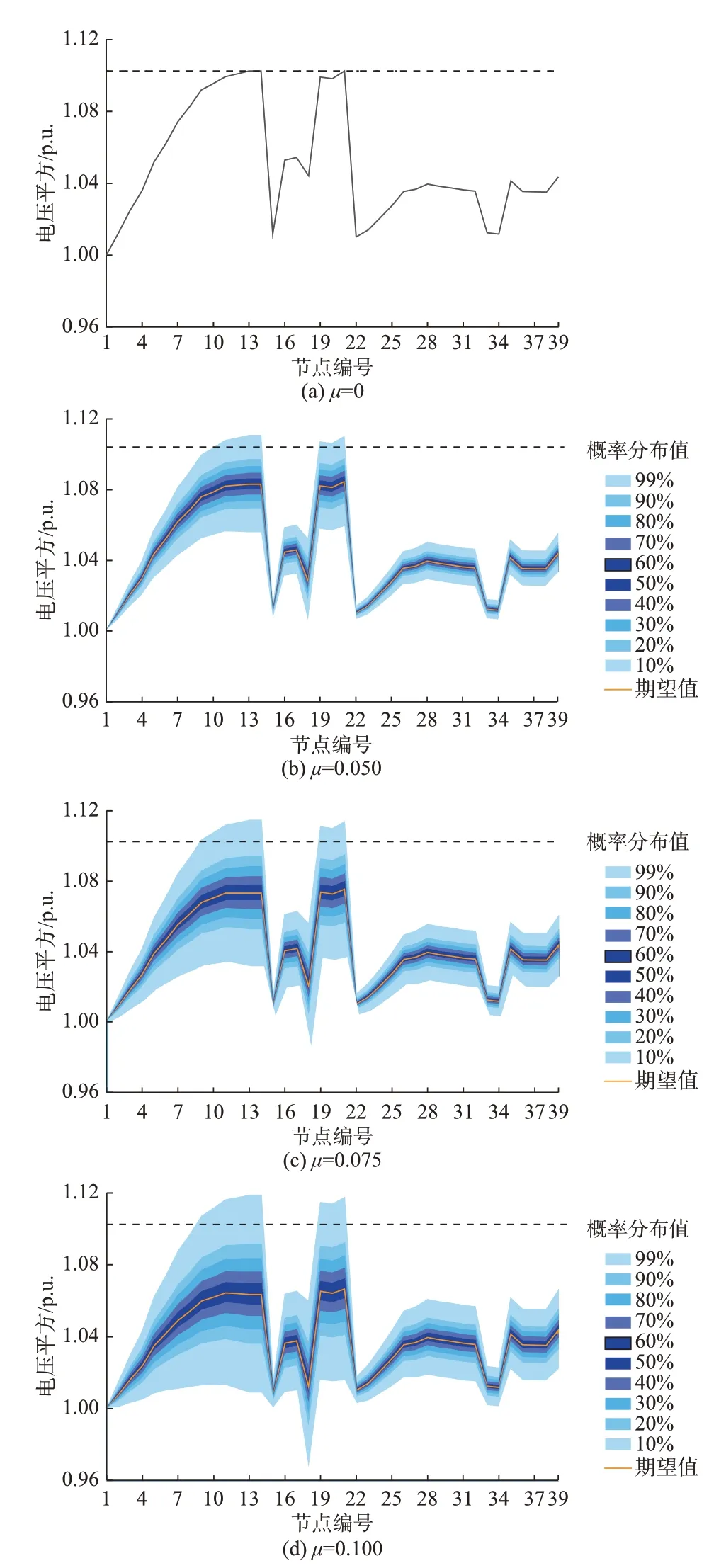
图4 不同预测精度下的电压平方分布Fig.4 Distribution of voltage square with different prediction accuracy

图5 中，由于预测精度相同，各子图中电压波动幅度一致，但随着消纳原则苛刻程度的增加，电压整体分布会有所下降，以降低电压越限的概率。

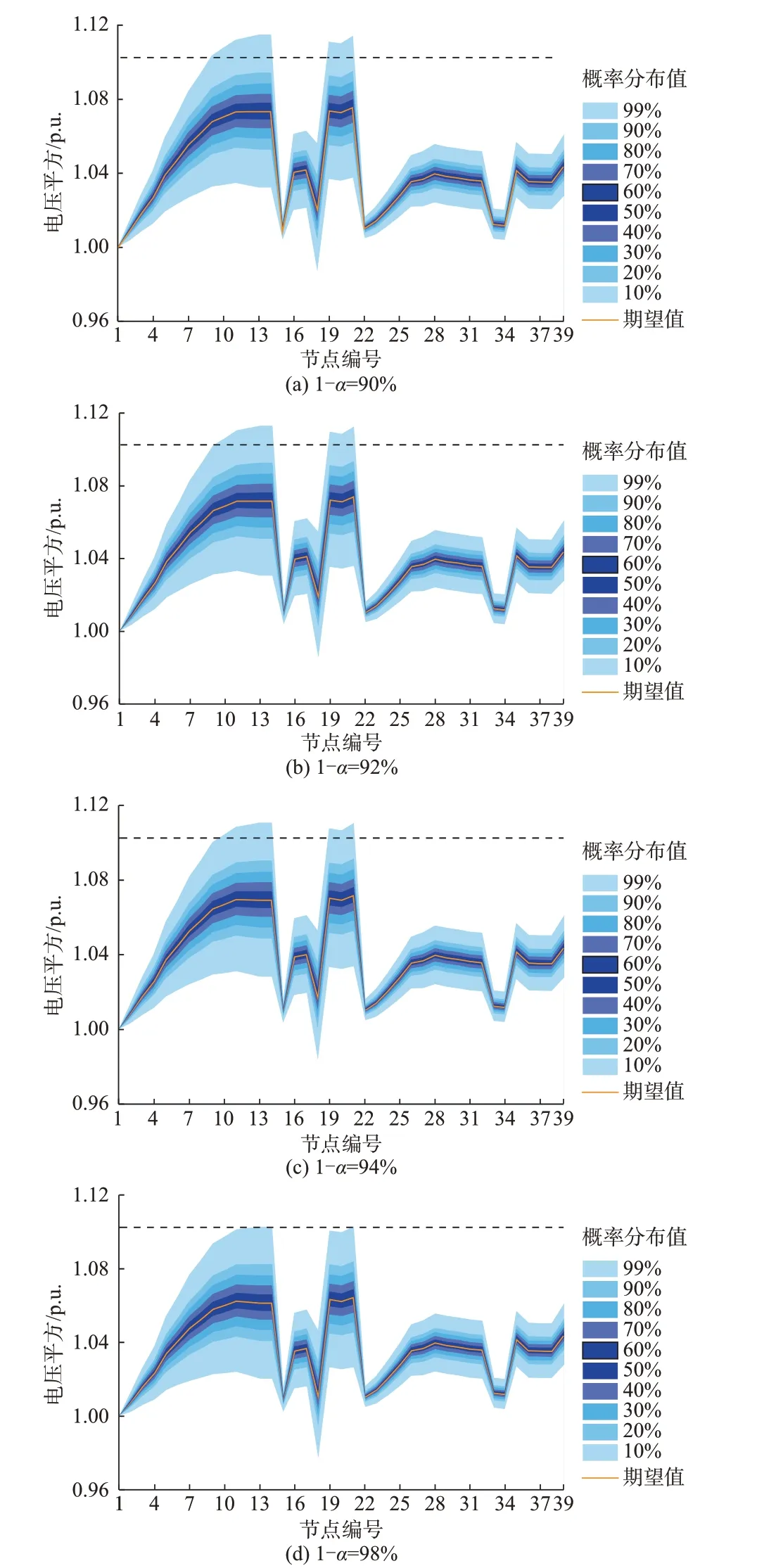
图5 不同消纳原则下的电压平方分布Fig.5 Distribution of voltage square with different accommodation principles

最后，对不同分布式能源渗透率下的消纳能力进行了分析。以附录A 表A3 中的装机容量为基准，分别分析了渗透率系数为0.6、0.8、1.0、1.2 等场景下的消纳能力，统一选取参数μ=10%，1-α=98%，分析结果如附录A 表A6 所示。可以看出，在渗透率系数为0.6 时仅出现少量切机，随着装机容量提升，消纳率大幅下降，当渗透率系数为1.2 时消纳比例仅为61.41%，该结论可以为分布式电源的规划提供参考依据。

5 结语

本文针对RDG 在配电网中渗透率逐步提高所导致的配电网运行不确定性增强和消纳能力不足等问题，提出了一种新型的配电网不确定性潮流分析思路，并基于此建立了考虑可再生能源功率不确定性的配电网消纳能力评估模型和方法，具体如下:

1）推导了配电网中注入功率不确定性与状态变量不确定性之间的映射关系，建立了当可再生能源功率不确定性用概率或仿射描述时，节点电压、支路功率等状态量相应的概率或仿射解析表达式。

2）基于不确定性潮流分析进一步建立了配电网RDG 消纳能力评估模型，提出了可再生能源功率不确定性用概率或仿射描述时消纳能力评估模型的等价转换方法，可以分析在不同的可再生能源功率预测精度和置信水平下配电网对于RDG 的消纳能力，并选取实际配电网系统算例对理论分析进行了验证。

同时需要指出，虽然本文提出的仿射潮流分析方法能够分析多节点注入功率波动存在相关性的场景，但概率潮流分析方法尚未考虑多节点功率注入量为非独立随机变量的场景。因此，可以进一步研究基于数值卷积和Copula 模型的概率分析方法，以获得考虑随机波动相关性时状态量的精确概率分布。另外，本文仅考虑了分布式电源的有功无功控制手段，但尚未考虑配电网中无功补偿、储能、网络重构等其他各类灵活性资源，将在后续工作中开展进一步研究。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。