隔震支座在房屋顶部加层改造中的应用

李晓玮 施卫星 虞终军

（1.同济大学建筑设计研究院（集团）有限公司，上海 200092；2.同济大学结构防灾减灾工程系，上海 200092）

0 引 言

在结构的改造工程中，经常遇到需要在已有建筑顶部新加一层的情况，比如在砌体结构顶层新增一层框架结构，用作会议室或者餐厅。当原结构周期位于地震影响系数曲线水平（接近Tg）或下降段时，按照传统的柱底插筋锚固加层方式，结构整体周期加大有利于降低地震影响系数，但是重力荷载代表值的显著增加会使各层层剪力增大，结构位移增加，砌体墙应力变大。在加层改造中，通常所加层的重量相当于下部结构的5%～20%，如果能将新加层当作附加于下部结构的调谐质量阻尼器（Tuned Mass Damper，TMD），反而可以起到控制下部结构的水平向振动的作用，减小下部结构的地震响应[1]。

现有隔震支座的研究大多集中于基础隔震和层间隔震，主要目的是减轻上部结构的地震响应，而新加层采用隔震支座的目的是控制下部结构的响应，同时限制隔震层位移[2]。铅芯橡胶支座是在普通叠层橡胶支座中插入铅芯，用以改善支座的阻尼性能，利用叠层橡胶较小的剪切刚度延长结构的周期，利用铅芯的塑性变形吸收能量[3]。摩擦摆支座主要是利用圆弧滑动面的设计来延长结构振动的周期，利用滑动面与滑块之间的摩擦来消耗能量[4]。本文通过建立加层结构的两自由度运动方程，从质量比、阻尼比和频率比等方面分析了不同隔震支座参数影响结构振动衰减的规律。

1 铅芯橡胶支座

铅芯橡胶支座的力学模型可以简化为弹簧和阻尼器，如图1所示，按常规TMD的力学模型加以分析。用两自由度体系表达的加层与下部结构的运动方程为

图1 两自由度运动体系简图Fig.1 Movement diagram of two degrees of freedom

式中：m0、mT为主体结构和TMD的质量；k0、kT为主体结构和TMD的刚度；c0、cT为主体结构和TMD的阻尼系数；xT为TMD相对主体结构的位移；x0为主体结构相对于地面的位移；ẍg为基底输入的地震加速度。

为得到结构的传递函数，令ẍg=eiωt，ω为输入荷载的圆频率，定义主体结构和TMD的位移响应为

式中，H0(ω)和HT(ω)是主体结构和TMD响应的传递函数。

假设基底输入的地震加速度是均值为零的白噪声过程，且其功率谱为常数S0，则结构的响应同样为白噪声过程。根据传递函数可求得结构的响应方差为[5]

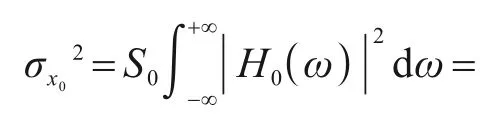
ω0、ωT是主体结构和TMD的圆频率，ξ0、ξT是主体结构和TMD的阻尼比，定义质量比μ=mT/m0。

对未设置TMD的单自由度系统，基底输入的地震加速度也是功率谱为S0的白噪声过程，其反应方差为[6]

假定设置TMD的结构反应方差和未设置TMD的结构反应方差之比为SR，SR可以作为评价TMD减振效果的指标，SR＜1表明TMD具有减振效果，而且越小效果越好。

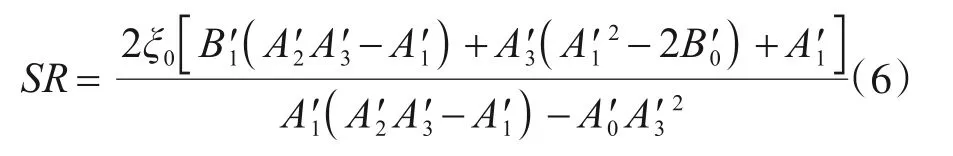
其中：f=ωT/ω0，A'0=f2，A'1=2ξ0f2+2ξTf2，A'2=1+(1+μ)f2+4ξ0ξTf，A'3=2ξ0+2(1+μ)ξTf，B'0=-(1+μ)f2，B'1=(1+μ)2f2。

为了分析TMD质量比、频率比和阻尼比对铅芯橡胶支座下部结构产生减振效果的影响，假设下部结构的质量m0=5 000 t，刚度k0=970 000 kN/m，阻尼系数c0=6 964 kN·s/m，取TMD质量比μ分别为 0.01，0.05，0.12，0.20；TMD 阻尼比ξT分别为0.01，0.03，0.05，0.07，0.10，0.13，0.15，0.17，0.20；TMD频率与主体结构频率比为0.1～2进行分析，得到结构的反应方差比[式（6）]如图2所示。

图2 主体结构的反应方差比Fig.2 Variance ratio of the response of the main structure

由图2可知，质量比在1%～20%之间随着质量比增加，TMD的减振效果也趋于更优；质量比较低时，阻尼比对减振率的影响表现为抛物线形，阻尼比在中间某处值时达到最优减振效果；质量比较大时，阻尼比对减震率的影响类似于两折线形，先上升后趋于平缓；而且要达到最优减振率，随着质量比增加阻尼比也要相应增加；随着质量比增加，最优频率比向小于1的方向移动，质量比越大，最优频率比越小；随着质量比增加，减振效果的离散性增加，如果参数选取不当会严重影响减振效果。综上所述，用铅芯橡胶支座加层时，由于质量比较大，应尽量选用阻尼比较大的方案，建议阻尼比取10%以上，频率比宜选择在0.8左右。

2 摩擦摆支座

摩擦摆的受力图可以简化为滑块作用于圆弧滑动面的形式，如图3所示，滑动面的圆弧半径为R，滑块质量为mT。θ是滑块相对滑动面竖向法线的夹角，xT为滑块离开中心点的位移，由于sinθ的表达式与xT有关，所以sinθ是有符号的，而且和xT一致。滑块受到自身重力G，滑动面的支撑力Gcosθ和摩擦力f=μGcosθsign(θ̇)作用，μ为摩擦系数。其中

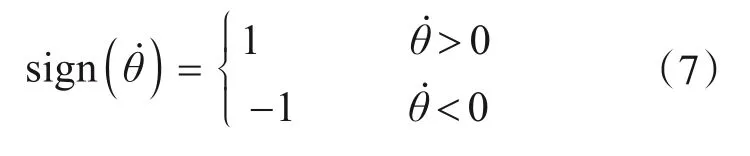
图3 摩擦摆支座力学简图Fig.3 Mechanical diagram of friction pendulum bearing

假定有一水平外力F作用于滑块上，对滑动面圆弧心O点取矩，即∑M0=0，可得式[7]：

该水平外力可以表示为

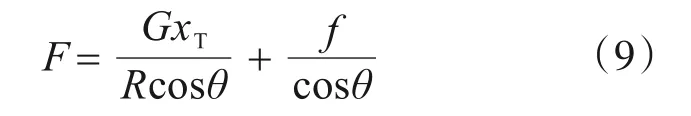
当假设滑块摆动夹角θ很小时，式（9）可简化为

因此，摩擦摆的刚度为

由式（10）以及摩擦摆各向对称性，可构造出滞回曲线模型，如图4所示。

图4 摩擦摆支座的滞回模型Fig.4 Hysteresis model of friction pendulum bearing

由滞回模型可以得到摩擦摆的等效线性刚度及等效黏滞阻尼比：

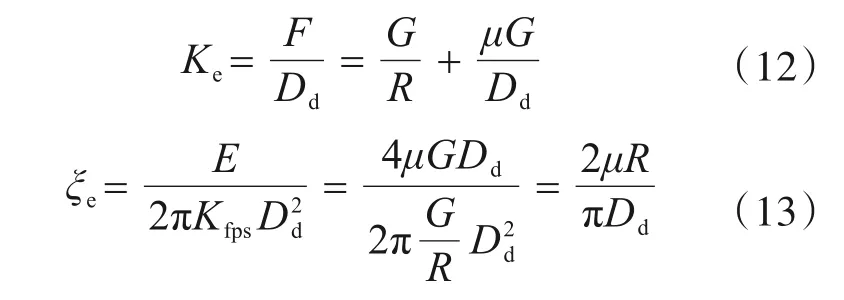
式（12）、式（13）中的Dd表示力-位移滞回环中的位移幅值，也即设计位移。

但是当滑块的摆角比较大时，cosθ≈1就不再适用，以单自由度结构串联一个摩擦摆体系为例，写出其运动方程为

由于式（14）非线性程度比较高，又有符号函数sign，所以采用NewMark-β法对方程进行时间积分求解。图5—图7所示为结构的功率谱密度曲线（以某一种工况为例）和不同参数时下部结构的最大加速度结果。

图5 摩擦系数对下部结构加速度的影响Fig.5 Influence of friction coefficient on the acceleration of substructure

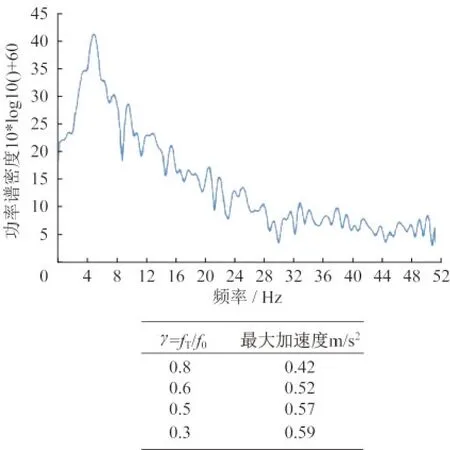
图6 滑动面半径对下部结构加速度的影响Fig.6 Influence of sliding surface radius on the acceleration of substructure

图7 质量比对下部结构加速度的影响Fig.7 Influence of mass ratio on the acceleration of substructure

2.1 摩擦系数的影响

当摩擦摆滑块位于滑动面中心位置附近时，若要滑块能够依靠其自身重力自动回复至中心点，自重恢复力需要克服摩擦力使之下滑，则有[8]：

当θ很小时，上式可简化为

式中，Dm为滑块接近中点的某个临界位移值，当Dm＞μR时滑块可在自重作用下自动恢复；当Dm=μR时恰好达到平衡，滑块停在中心点附近，此时Dm即为滑块的最大残余变形。由式（16）可知，摩擦摆的残余变形与摩擦系数和滑动面半径有关。通常设计摩擦摆时都会使摩擦系数尽量小，此时残余变形也很小，可以忽略不计。通过添加润滑剂或者采用聚四氟烯板等技术可以使摩擦系数达到0.01以下。

为了分析摩擦系数会对摩擦摆支座下部结构产生的影响，分别选用μ=0.005，0.01，0.015，0.02。下部结构的质量m0=5 000 t，刚度k0=970 000 kN/m，阻尼系数c0=6 964 kN·s/m，支座上部结构质量mT=600 t。式（12）中项相对于通常很小，如果忽略此项产生的误差在10%以内，所以初步拟定摩擦摆半径时可以采用下式：

将摩擦摆和上部结构当做调谐质量阻尼器时，需要摩擦摆的频率与主体结构频率一致，即由所计算出的频率是主体结构频率的0.8倍，即半径R=0.08 m。

如果改变摩擦系数的取值，由图5可以得到结论[9]：随着摩擦系数的增大，支座下部结构加速度响应频谱峰值增大，隔震结构向非隔震结构退化，对于支座下部结构隔震效果减弱，并且加速度峰值处的频率随着摩擦系数增大而增大，最终接近非隔震结构的无阻尼自振频率。

2.2 滑动面半径的影响

摩擦摆系统的频率近似表达为

可知，其频率只与半径R有关。假设γ=fT/f0，f0为主体结构频率，通过选取γ=0.8，0.6，0.5，0.3，半径分别为0.052 m，0.08 m，0.14 m，0.27 m，0.56 m，分析其对下部结构加速度的影响。需注意，对于加层来说，当γ=1.0时，通常所计算的R值较小，可能在较大地震作用下，支座上部结构的位移会超过摩擦摆的位移限值，所以本文选取γ＜1的参数进行分析。

对于支座上部结构，随着摩擦摆半径的增大，上部结构的恢复刚度减弱，结构整体变得更柔，加速度响应峰值变小，但减小的程度随半径增大而减小[9]。由图6可得，摩擦摆频率的表达式（18）对支座下部结构的影响与传统TMD是一致的，当频率比γ在0.8附近时，加速度响应最小，当γ小于0.5以后这种差异逐渐缩小。

2.3 质量比的影响

如图7所示，与传统TMD一样，随着质量比增加，下部结构加速度响应减小。对于摩擦摆支座上部结构，随着质量比的增加，加速度影响峰值也会减小。实际工程中质量比通常取决于加层方案，大幅度调整的可能性不大。

3 各种加层方案的对比

已有一位于上海地区（7度0.10g，场地类别：第一组，Ⅲ类场地土）的6层砌体结构房屋，1层地下室。砌体墙厚240 mm，采用烧结普通砖，砌体墙上设圈梁，窗、门洞间墙设构造柱，圈梁和构造柱采用C20混凝土。该建筑平面呈矩形，长43.2 m，宽12 m，层高2.8 m，地面以上总建筑高16.8 m，一层地下室高2.8 m。该建筑由于使用需要在顶部增加一层，层高3 m，所加层采用框架结构形式。框架柱截面为300×300，框架梁截面为200×300，均采用C30混凝土。砌体建筑及加层轴测图见图8。

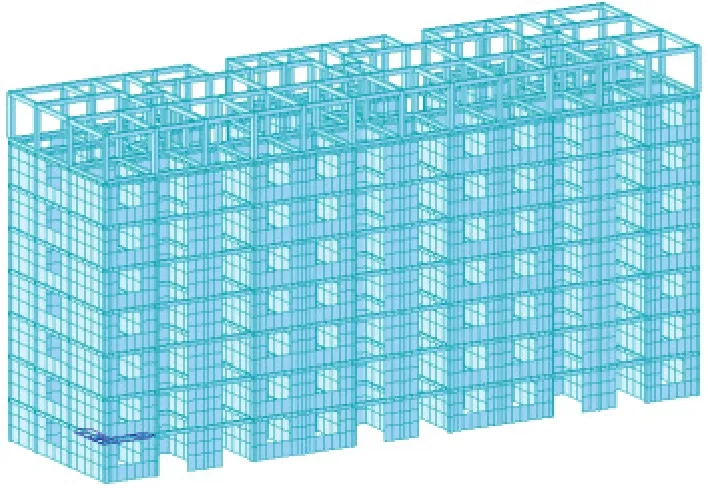
图8 多层砌体结构加层轴测图Fig.8 Axonometric Sketch of the masonry structure adding a layer

模型中圈梁和构造柱按照杆件单元建立，砌体墙采用了墙单元，厚度按照实际墙厚，材料的弹性模量取3024 MPa，泊松比为0.15，容重为22 kN/m3。该结构模型只能在弹性理论范围讨论砌体墙的抗侧性能和动力特性，并不能真实反映砌砖、砂浆等材料的不确定性以及构造的复杂性。鉴于砌体结构目前尚无合理的分析模型，且本文主要分析隔震支座对结构的减震的规律，所以对该砌体结构的简化建模并不影响得到的结论。

传统加层方案即在顶层砌体墙上增设圈梁，混凝土柱直接落在圈梁上，在构造上保证柱纵筋在底部有充足的锚固，使加层与下部结构形成整体。

采用摩擦摆支座时，为了使加层尽量发挥TMD的效应，即支座周期与下部结构协调，摩擦摆支座的半径设计为49.3 mm，速度慢时的摩擦系数0.015，速度快时的摩擦系数0.01。由式（18）计算的支座频率，约为主体结构频率f1（2.27 Hz，Y向平动）的0.98倍和f2（3.03 Hz，X向平动）的0.74倍。每个柱底布置相同参数的摩擦摆支座共62套，见图9。隔震层下端砌体与上端框架连接示意图如图10所示。

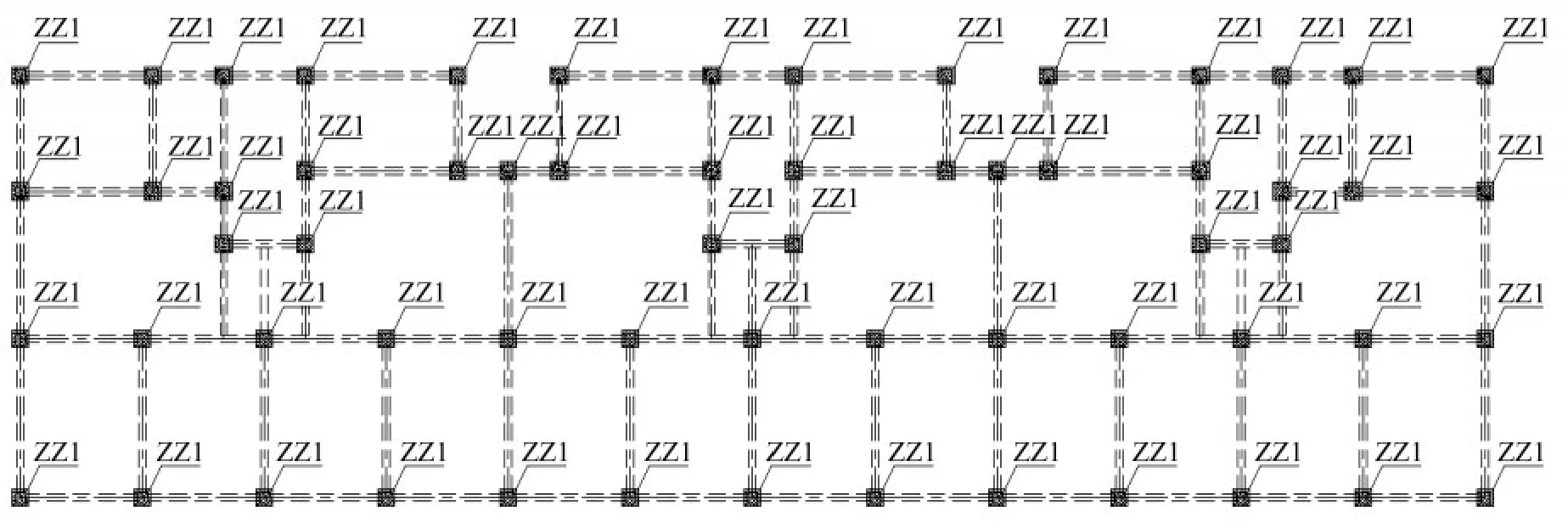
图9 隔震层支座布置图Fig.9 Layout of isolation supports

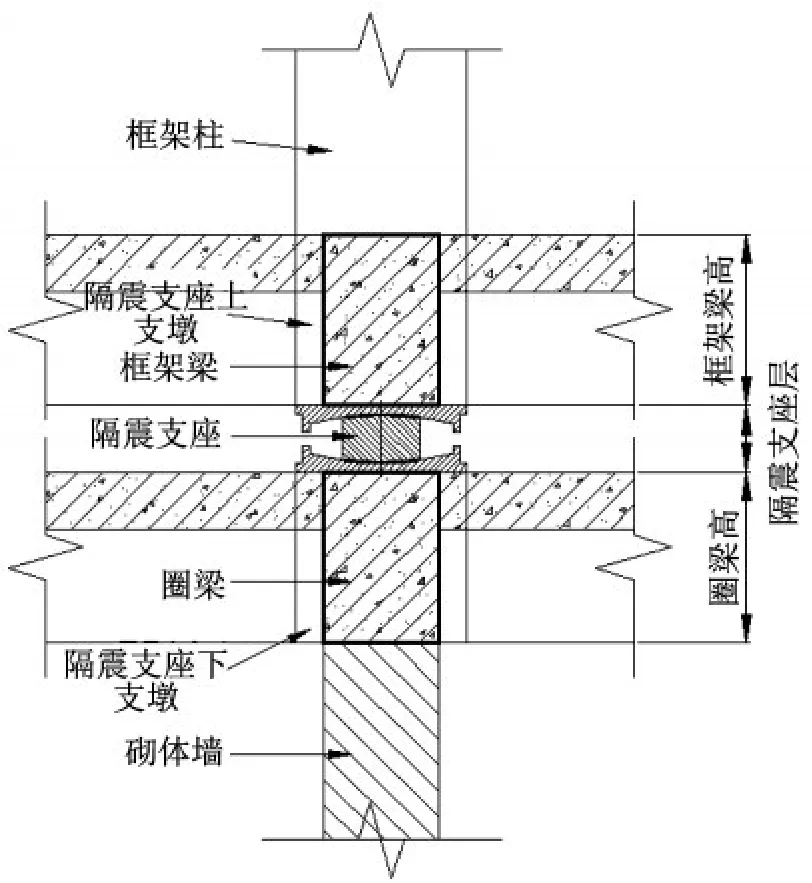
图10 隔震支座层构造示意图Fig.10 Diagram of isolation bearing layer

由于顶层加层改造中，所加层重量比较小，框架梁柱尺寸也较小，所以对铅芯橡胶支座的尺寸一般会有限制。本工程中加层框架柱截面尺寸为300×300，选用Ф300的铅芯橡胶支座，布置在62根框架柱底，支座性能见表1，布置见图9。铅芯橡胶支座层的频率fT=1.29 Hz，约为主体结构频率f1的0.57倍和f2的0.43倍。

表1 铅芯橡胶支座参数Table 1 Parameters of Lead Rubber Bearing

本项目采用了5条强震记录和2条人工模拟加速度时程曲线作为地震动输入，后续计算结果均为7条地震波弹塑性分析结果的平均值。表2—表9为不同加层方案下，结构的周期、基底剪力、砌体顶层、新加层位移和加速度以及底层砌体墙应力的对比结果。图11所示为各加层方案中下部砌体墙的应力云图。

表2 各种方案下周期对比Table 2 Comparison of period of different case s

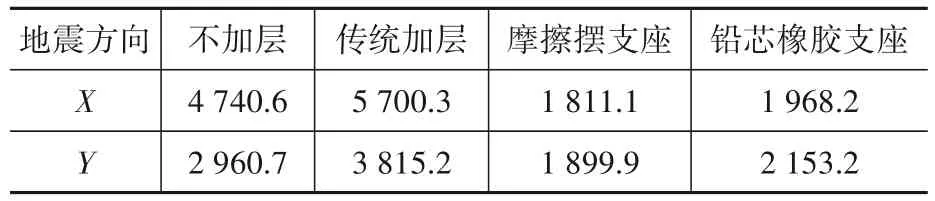
表3 各种方案下基底剪力对比Table 3 Comparison of base shear of different case kN

表4 各种方案下砌体顶层位移对比Table 4 Comparison of the top-layer’s drifts of different case mm

表5 各种方案下砌体顶层加速度对比Table 5 Comparison of the top-layer’s acceleration of different case cm/s2

表6 各种方案下新加层位移对比Table 6 Comparison of the adding-layer’s drifs of different case mm

表7 各种方案下新加层加速度对比Table 7 Comparison of the adding-layer’s acceleration of different case cm/s2

表8 各种方案下隔震支座位移对比TabLE 8 Comparison of the isolation-layer’s drifts of different case mm

表9 各种方案下底层砌体墙应力对比Table 9 Comparison of stress of bottom masonry wall among several programmes MPa

图11 各种方案砌体墙应力图Fig.11 Stress diagram of masonry walls

综合比较四种方案，即不加层结构、传统加层、摩擦摆支座加层和铅芯橡胶支座加层结构，在相同的地震波作用下，由表2—表9可以看出传统加层结构的基底剪力、砌体顶层位移和墙体最大应力都比不加层结构的大，而摩擦摆和铅芯橡胶支座结构的结果都比不加层结构的小，也就是说采用隔震支座以后，下部结构的响应反而比原来的更小。具体为，摩擦摆支座基底剪力与不加层结构相比减小61.8%（Y方向35.8%），铅芯橡胶支座基底剪力减小58.5%（Y方向27.3%），摩擦摆支座结构的墙体最大应力比不加层结构减小62.73（正应力）和62.0%（负应力），铅芯橡胶支座结构的墙体最大应力比不加层结构减小51.9%（正应力）和57.8%（负应力）。对于砌体顶层加速度和位移，以及新加层加速度，两种隔震支座方案总体差别不明显，但均好于传统加层结构。对于隔震支座位移，摩擦摆支座优于铅芯橡胶支座。需要注意的是，在本项目中由于受限于支座尺寸，摩擦摆支座的刚度特性更趋近于TMD的要求，所以减振效果略优于铅芯橡胶支座。

4 结 语

本文针对加层改造案例进行了专项分析，提出可以在原有结构顶部和新加层之间设置隔震支座，此时新加层相对原结构具有TMD的效应，可以减小下部结构的地震响应。通过分析对比可知，无论采用何种隔震支座形式，下部结构的各项地震响应均远比不加层和刚性加层结构小；各种隔震支座下结构响应略有差异，隔震支座的频率越接近于最优频率（下部结构频率的0.8倍），阻尼比在10%～20%区间取值越大，摩擦摆支座滑动系数越小，原结构和新加层响应越小。