大跨越输电塔四钢管组合柱稳定承载力研究

甘懿德 邓洪洲 李秉泽

（同济大学建筑工程系，上海 200092）

0 引 言

为了满足经济发展带来的日益增长的用电需求，新建输电线路电压等级越来越高，输电铁塔日趋大型化，其荷载也相应增大。苏通长江大跨越工程中拟建的两座跨越塔，设计塔高455 m，档距2 600 m，塔脚处主材轴力设计值达到2.5×105kN。如果仍然采用传统的单钢管混凝土主柱，主柱最大截面将达到Φ2 750 mm×44 mm，不仅难以加工、运输和施工，还伴随着截面过大带来的局部稳定问题和过厚钢材层状撕裂问题。因此，该大跨越工程设计阶段提出了如图1所示的四管组合柱方案，即在变坡节点以下采用由四根较小直径主管通过钢连梁连接形成的四管组合柱来作为输电塔的主要受力构件。

输电塔四钢管组合柱主要承受轴压力，采用连梁连接，受力接近缀板柱。而由于输电塔工程自身特点限制，组合柱长细比、分肢间距小，缀板分肢线刚度比不能满足现有规范中缀板柱计算公式的要求。因此对于四管组合柱这种新式的输电塔主柱，如何计算稳定承载力以及确定合理的连梁线刚度成为其应用过程中的需要解决的主要问题。

图1 苏通大跨越四钢管组合柱输电塔（单位：mm）Fig.1 Sutong large-span transmission tower（Unit：mm）

组合构件稳定承载力研究较为成熟。Engesser最早提出了考虑剪切变形影响的实腹柱弹性屈曲荷载公式；Timshenko[1]通过假定反弯点在缀板和分肢中心将该方法引入组合柱稳定计算中，目前对于多种形式格构柱的稳定承载力研究均采用此种方法[2-4]。此外，一些学者还提出了不同于Engesser法的组合构件计算方法，如Tong等[5]提出的格构柱修正夹层梁理论、Gjelsvik[6]给出的组合柱的六阶控制方程、A.G.Razdolsky[7]采用的组合柱整体分析法。

组合柱目前主要有两种设计方法。一种是《钢结构设计标准》（GB 50017—2017）[8]所采用的换算长细比法，另一种是欧洲钢结构规范[9]采用的单肢验算法。换算长细比方法通过组合柱换算长细比查阅稳定系数，从而计算弹塑性稳定承载力。该方法的优势是简单直观，缺点是假设了组合柱初始缺陷与实腹柱相同，不能考虑组合柱分肢受力不均的影响。而单肢验算法则能考虑此种缺陷的影响。

本文根据输电塔四管组合柱特点，首先在考虑初弯曲的单肢验算法基础上推导了考虑初弯曲和初偏心的单肢验算法公式；其次以有限元弹性屈曲分析为依据研究了不同换算长细比公式的适用性，并结合组合柱弹塑性屈曲有限元分析研究了基于不同换算长细比公式的换算长细比法和单肢验算法公式的适用性；最后以苏通大跨越输电塔为案例，对组合柱弹塑性稳定承载力计算方法进行验证。

1 四管组合柱计算方法

1.1 Engesser法

1.2 单肢验算法

单肢验算法是计算组合柱弹塑性稳定承载力的主要方法之一。考虑到输电塔四管组合柱长细比较小，初偏心对稳定承载力影响较大，四管组合柱绕45°对管方向弯曲时对分肢主管受力最为不利，因此在计算模型中假设四管组合柱在45°对管方向有等效初弯曲和端部初始偏心e，如图2所示。

图2 分析模型Fig.2 Analysis model

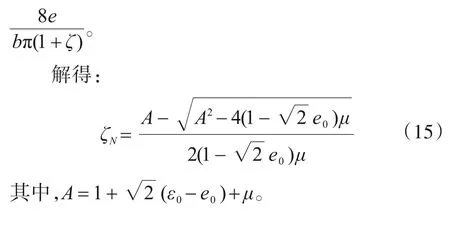
2 有限元分析

在输电塔四钢管组合柱参数范围下，结合有限元分析对仅考虑缀板和分肢弯曲的换算长细比公式[式（4）]、考虑缀板和分肢弯曲及缀板剪切的换算长细比公式[式（3）]以及计算弹塑性稳定承载力的换算长细比法和单肢验算法进行对比验证，并通过有限元分析线刚度比对输电塔组合柱弹塑性屈曲荷载的影响。

输电塔四钢管组合柱分析参数规定如下。分肢主管截面取为Φ800 mm×20 mm，分肢净间距取400～800 mm以满足最小施工间距要求并保证组合柱整体性。组合柱线刚度比范围为1≤k≤6，名义长细比范围10≤λ≤160。为了避免分肢失稳，分肢长细比均满足GB 50017—2017的要求。分肢主管和工字连梁的材料分别为Q420、Q345钢。计算模型中，为了便于对组合柱作规律性分析，柱端约束假定为铰接。由于实际输电塔钢管柱长细比小，柱端约束有一定刚度，为了考虑端部弯矩的影响，在弹塑性屈曲分析时同时设置了初弯曲和初偏心两种缺陷。

本研究采用ANSYS开展输电塔组合柱有限元分析。有限元模型如图3所示，其中主管和工字连梁均采用SHELL181单元划分网格，并在组合柱端部将主管结点耦合在一起实现组合柱的整体铰接。材料模型均采用理想弹塑性模型，弹性模量为206 GPa，泊松比为0.3，主管、连梁钢材屈服强度分别为420 MPa、345 MPa。根据网格无关性分析结果，有限元模型中主管和连梁网格大小分别为100 mm、150 mm。

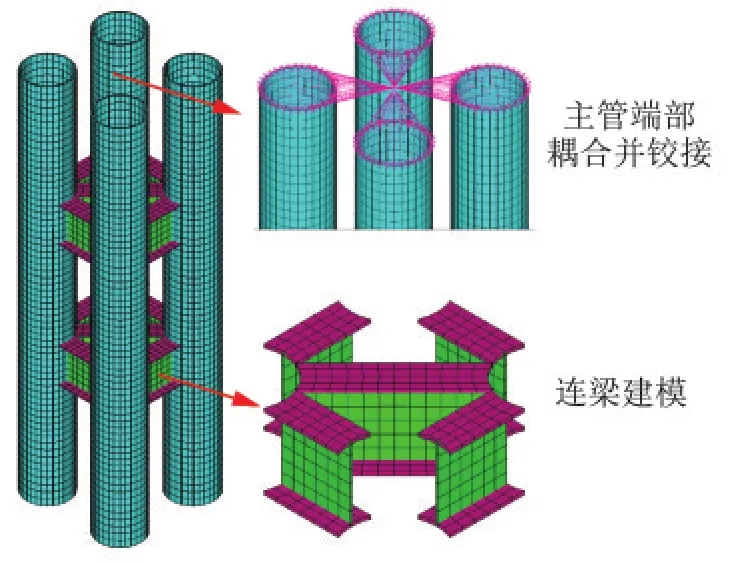
图3 有限元模型Fig.3 Finite element model

弹性屈曲有限元分析中，在组合柱端部耦合节点施加集中力以模拟轴向荷载，并取第一阶弯曲屈曲模态对应的临界荷载作为该组合柱的弹性屈曲荷载。弹塑性屈曲有限元分析中考虑了材料非线性、几何非线性以及初始缺陷。由于输电塔组合柱长细比较小，初偏心的初始缺陷对组合柱承载力的影响较大[1，12]，因此根据文献[1]将组合柱的初始缺陷取为

其中，初始偏心通过在柱两端加载弯矩进行施加，初始弯曲通过一致模态法施加，输电塔组合柱弹塑性稳定承载力根据非线性分析荷载-位移曲线的峰值确定。

2.1 弹性屈曲荷载对比

在组合柱弹性屈曲有限元分析中，当λ＜10时组合柱的第一阶屈曲模态可能为主管的局部失稳或局部失稳与整体弯曲失稳的组合。为了使结果对比更有意义，在后续分析中将只列出第一阶屈曲模态为组合柱整体弯曲的结果。

图4、图5分别给出了式（4）、式（3）计算得到的组合柱弹性屈曲荷载与有限元分析结果的相对误差，其中负号表示比数值结果小。整体来看，式（3）和式（4）的相对误差随着组合柱长细比的减小而增大。在λ＜40时，不考虑缀板剪切变形[式（4）]的结果明显大于有限元结果，且这种偏差随着间距比的增加而增大。而考虑缀板剪切变形[式（3）]的结果与式（4）相比则更偏于安全；虽然在分肢净间距较大（dn=800 mm）时式（3）结果相较于有限元也会偏大，但整体偏大不超过5%。

图4 式（4）计算的弹性屈曲荷载与有限元对比Fig.4Comparison between Eq.（4）and finite element analysis

图5 式（3）计算的弹性屈曲荷载与有限元对比Fig.5Comparison between Eq.（3）and finite element analysis

此外，式（3）、式（4）的相对误差还随着线刚度比的减小而增大。对于式（3）的对比结果，k＜3时相对误差才会明显增加。

2.2 弹塑性屈曲荷载对比

图6给出了dn=400 mm、k=1时由换算长细比法、单肢验算法和有限元分析得到的输电塔组合柱柱子曲线。在应用换算长细比法时分别按式（3）、式（4）计算换算长细比。可以看到，采用式（3）的换算长细比法得到的组合柱稳定承载力更偏于安全，而采用式（4）的换算长细比法和单肢验算法与有限元分析结果接近。

图6 输电塔组合柱柱子曲线（dn=400 mm，k=1）Fig.6 Column curves（dn=400 mm，k=1）

图7给出了不同设计方法与有限元结果的相对误差以作详细对比，其中负值表示计算结果与有限元相比偏小，即偏于安全。总体而言，采用按式（3）、式（4）设计的换算长细比法和单肢验算法与有限元结果相比误差都相对较小。其中按式（4）设计的换算长细比法与有限元结果偏差最小，但在λ＜20时可能偏于不安全；按式（3）设计的换算长细比法整体偏于安全，但在λ＞30时相对误差较大；单肢验算法结果与有限元结果相比整体偏于不安全，这表示在本研究参数范围内和初始缺陷条件下组合柱弹塑性稳定承载力不易由分肢失稳控制。此外，线刚度比k=3时换算长细比法结果的相对误差与k=6时接近，表明该方法在小线刚度比条件下的适用性。

图7 弹塑性屈曲荷载计算式与有限元对比Fig.7 Comparison between equivalent slenderness ratio method，chord-checking method and finite element analysis

2.3 线刚度比影响

采用有限元分析得到线刚度比为k时组合柱弹塑性屈曲荷载Ncrk，并以k=6时的屈曲荷载Ncr6为基准计算k＜6时组合柱承载力相对变化，结果如图8所示。显然，随着输电塔线刚度比的减小输电塔组合柱弹塑性稳定承载力逐渐降低，并且k越小这种降低趋势越明显。总的来看，当线刚度比不小于3时承载力降低最大为3%，因此考虑经济性要求组合柱连梁线刚度宜取为3。

图8 不同线刚度比下组合柱承载力较k=6时的变化Fig.8 The change of elastoplastic stability bearing capacity withkdecrease（compared withk=6）

3 算 例

本部分结合苏通大跨越四钢管组合柱输电塔案例，对组合柱弹塑性承载力设计方法进行对比验证。苏通大跨越输电塔钢管塔型方案如图1所示。该塔型方案中四钢管组合柱的具体参数如表1所示，其中组合柱线刚度比均为3。

表1 四管组合柱参数Table 1 The parameters of four-tube built-up column

针对表1所示的不同组合柱，分别采用按式（3）、式（4）设计的换算长细比法和单肢验算法得到其稳定系数，并与有限元分析结果进行对比，结果如表2所示。结果表明，按式（3）设计的换算长细比法与有限元结果相比更偏于安全；而按式（4）设计的换算长细比法和单肢验算法与有限元结果相比误差更小，但在λ＜10时可能偏于不安全。

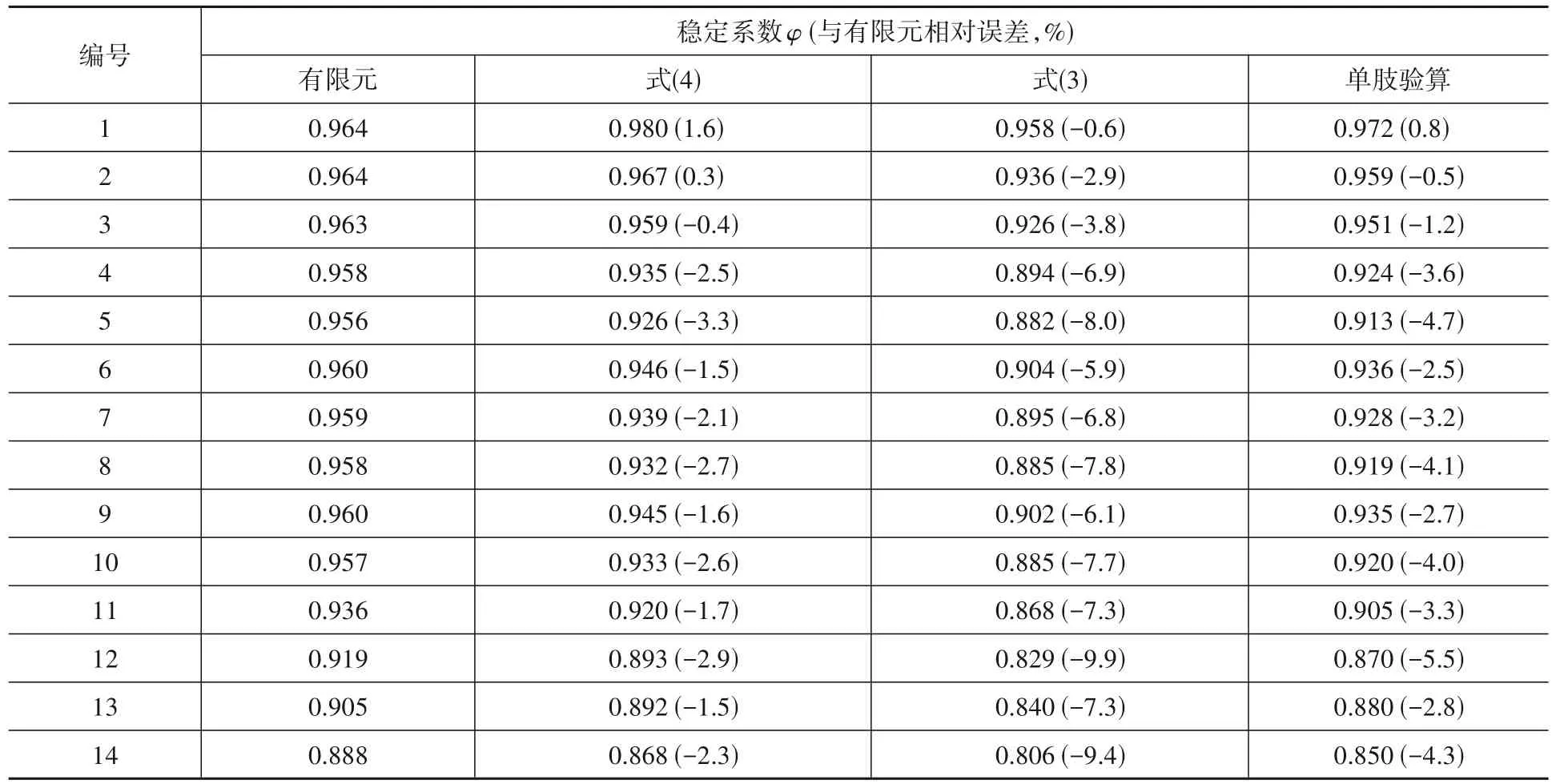
表2 不同设计方法与有限元的稳定系数对比Table 2 Comparison of stability coefficient between different design methods and finite element analysis

4 结论

本文根据输电塔四钢管组合柱的初始缺陷特点给出了考虑初弯曲和初偏心的单肢验算法计算公式，并结合有限元计算分析对比了输电塔四管组合柱弹性和弹塑性稳定承载力计算式的适用性，主要结论如下：

（1）组合柱弹性屈曲分析中，换算长细比公式考虑缀板剪切时[式（3）]的结果和不考虑时[式（4）]的结果相比，与有限元数值解符合得更好，建议按式（3）计算输电塔组合柱弹性屈曲荷载。

（2）输电塔四管组合柱线刚度比应不小于3，此时组合柱相对于k=6时的承载力降低最大为3%，且由换算长细比计算公式得到的结果误差更小。

（3）组合柱弹塑性屈曲分析中，不考虑缀板剪切影响的换算长细比法结果与有限元结果偏差最小，但在组合柱长细比较小时可能偏于不安全；考虑缀板剪切影响的换算长细比法与有限元结果相比整体偏安全，但在λ＞30时可能过于保守；单肢验算法结果与有限元结果相比整体偏大。

（4）在苏通大跨越输电塔组合柱计算中，当组合柱名义长细比小于10时建议考虑缀板剪切影响，长细比大于10时可按不考虑缀板剪切的换算长细比法或单肢验算法计算。