基于三维实体元的预应力混凝土变截面桥梁长期性能分析
2022-07-26李金国厉勇辉牛伟迪
李金国 厉勇辉 牛伟迪
(1.同济大学建筑设计研究院(集团)有限公司,上海 200092;2.中交第二航务工程局有限公司,武汉 430040)
0 引 言
在目前的工程实践中,跨径在50 m以下的预应力混凝土桥梁中,多采用空心板、小箱梁和T形截面梁等装配式结构,跨径在50 m以上时,一般采用预应力混凝土(Prestressed Concrete,PC)变截面梁桥,其跨径已突破300 m。然而,长期的运营实践证明,大跨PC变截面梁桥的使用状况不容乐观,存在跨中下挠过大、梁体开裂等诸多病害[1]。例如,位于帕劳共和国的KB桥(全称Koror Babelthuap Bridge),1977年建成,运营18年后跨中下挠达1.61 m,加固3个月后突然倒塌,引起国际桥梁界广泛关注[2]。收缩徐变是混凝土结构基本特性,是影响PC变截面梁桥长期下挠和应力变化重要因素。
自1887年法国科学家Henri在研究硬化硅酸盐水泥浆体硬化过程发现收缩现象和1907美国Kendrick Hatt教授在普渡大学发现混凝土徐变效应后[3],国内外学者对混凝土收缩徐变开展了大量研究,为了能定性描述混凝土收缩徐变发展过程,提出大量的理论模型,主要包括CEB-FIP MC78/MC90/MC99、 ACI209R-82、 ACI209R-92、Bažant和 Panula的 BP、BP-2 模型、B3 模型等[4]。尽管国内外已经提出大量混凝土收缩徐变模型,但是很难准确描述实桥的混凝土收缩徐变作用,主要有以下几个原因[5]:①影响混凝土收缩徐变因素较多,为了便于工程应用,计算模型只考虑少量的因素;②目前收缩徐变模型都是通过短期实验数据得到,基于短期试验数据拟合得到的混凝土收缩徐变模型很难适用于长期徐变作用;③目前PC变截面梁桥采用的混凝土一般是高强混凝土,相应的实验结果非常少,适用于普通强度混凝土的收缩徐变经验模型不再适用;④桥梁处在变温、变湿和车载循环的环境中,与实验室环境差别较大,混凝土实际收缩徐变与实验结果相差较大;⑤PC变截面梁桥顶、底板和腹板理论厚度差异较大,顶、底板剪力滞效应比较明显以及合龙束张拉后存在锚后拉应力,采用杆系模型不能真实反映收缩徐变作用下结构长期挠度和应力状态。
1 不同收缩徐变模型对比分析
目前较常用的收缩徐变模型有ACI209、CEBFIP和B4模型。ACI模型是Branson和Christiason教授在1971年提出的,并于当年得到ACI委员会推荐。其后经过一些修改,陆续出现了ACI209R-82(1982年)和ACI209R-92(1992年)两种计算模型。ACI209模型采用渐进接近终止值双曲线函数形式进行表达[6]。B4模型是美国西北大学Bažant教授在B3模型的基础上修正得到的。B3徐变模型根据混凝土的固化理论建立,该理论是将弹性理论、黏弹性理论和流变理论结合起来,模拟混凝土宏观物理力学性质因水泥水化、固相物增多随时间不断变化的新理论,并结合全世界1 400个徐变实验和1 050个收缩实验数据拟合得到收缩徐变计算公式。CEB收缩徐变模型是在Muller和Hilsdorf教授1990年提出的CEB MC90模型基础上发展而来的,该模型和ACI209R-92收缩徐变模型较为相似,均是采用一个收缩徐变终极值和渐进曲线相乘得到。我国现行预应力混凝土设计规范的收缩徐变模型是在CEB-FIP(1990)模型基础上适当简化、修正得到的[7-10]。三种收缩徐变模型主要考虑的因素如表1所示。

表1 三种收缩徐变模型影响因素Table 1 Influencing factors of three shrinkage and creep models
B4模型相较ACI209和CEB-FIP(1990)模型考虑影响因素多,CEB-FIP(1990)模型未考虑水灰比影响、ACI209模型未考虑混凝土强度影响。
水灰比是影响收缩徐变的重要因素,我国现行规范未考虑水灰比对收缩徐变特性的影响。拟定构件理论厚度为100 mm,环境相对湿度70%,在混凝土强度均为C50的情况下,有A、B、C三个混凝土试块,水灰比分别为 0.43、0.39、0.35,ACI209和B4模型在三个试块的混凝土收缩徐变变化曲线如图1、图2所示,三种收缩徐变模型收缩应变和徐变系数对比如图3所示。
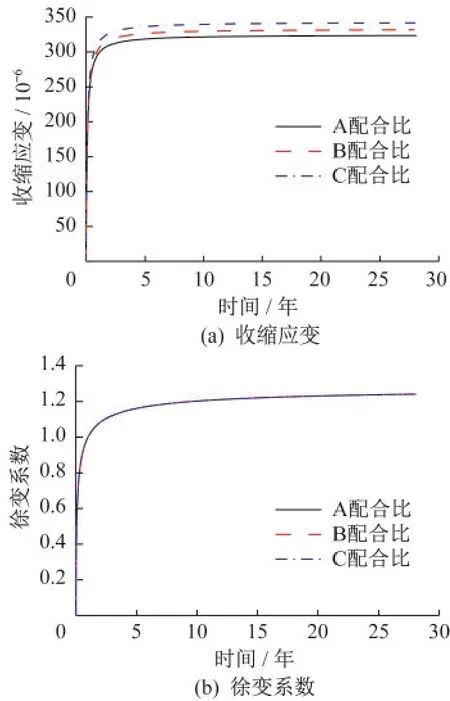
图1 ACI209不同水灰比下收缩应变和徐变系数Fig.1 Shrinkage strain and creep coefficient of ACI209 under different water cement ratio

图2 B4不同水灰比下收缩应变和徐变系数Fig.2 B4 shrinkage strain and creep coefficient under different water cement ratio
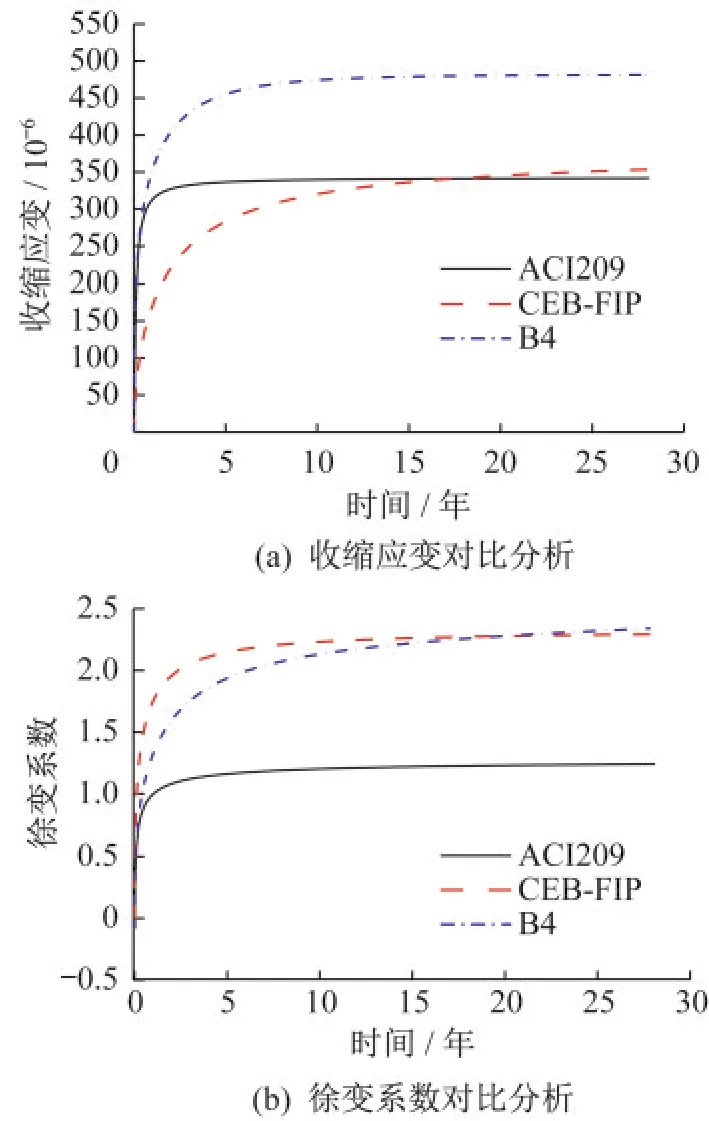
图3 A配合比下三种收缩徐变模型收缩应变和徐变系数对比分析Fig.3 Comparative analysis of shrinkage strain and creep coefficient of three shrinkage and creep models under mix proportion A
由上可以得到:
(1)ACI209模型中徐变系数不考虑水灰比的影响,水灰比对B4模型收缩应变和徐变系数影响较大。收缩应变随水灰比增加而变小,徐变系数随水灰比增加而增加。
(2)三种模型收缩应变均表现为前期发展快、后期发展慢,并逐渐趋于稳定的变化趋势。ACI209收缩应变发展较快,在第2年趋于稳定;CEB-FIP(1990)和B4模型的收缩应变在第10年左右逐渐趋于稳定。
(3)三种模型徐变系数和收缩应变的变化趋势基本相同,均表现出前期增长速率较快,后期增长速率慢的特点,ACI209模型在第5年趋于稳定,CEB-FIP(1990)模型徐变系数在第10年趋于稳定,B4模型徐变系数在后期一直处于增长的趋势。在A配合比下,ACI209模型徐变系数最小,B4和CEB-FIP(1990)模型第30年徐变系数基本相同,但后续徐变系数增加速率明显高于CEBFIP(1990)。
2 子程序开发
美国Bažant教授将混凝土结构收缩徐变敏感程度近似分为5个等级,如表2所示。对于属于Ⅰ、Ⅱ和Ⅲ等级内的混凝土结构,可采用简单收缩徐变模型分析,例如ACI209和CEB-FIP(1990),对于比较敏感的Ⅳ和Ⅴ结构应采用B3或者B4模型进行分析[11]。PC变截面梁桥一般属于Ⅳ和Ⅴ等级结构,对混凝土收缩徐变较为敏感,应采用实体元分析。

表2 混凝土结构收缩徐变敏感程度等级划分Table 2 Classification of shrinkage and creep sensitivity of concrete structure
Fortran语言与ABAQUS有限元软件有良好的交互性,采用Fortran语言开发ABAQUS混凝土收缩徐变子程序,并利用ABAQUS实体元模型分析PC变截面梁桥在收缩徐变作用下的时变效应。利用ABAQUS子程序中UMAT和UEXPAN功能分别模拟ACI209R、CEB-FIP(1990)和B4三种收缩徐变模型中的收缩和徐变。首先通过比较混凝土收缩徐变的解析解和ABAQUS有限元模型计算的数值解,以验证二次开发收缩徐变子程序正确性。为此,建立一个1 m×1 m的一个实体元单元ABAQUS有限元模型,并在上表面施加1 MN的均布力,单个实体元模型竖向位移提取点如图4所示。

图4 ABAQUS收缩徐变子程序校核分析模型Fig.4 ABAQUS shrinkage and creep subroutine verification analysis model
利用子程序得到的数值解与解析解对比如图5—图7,可以看出,二次开发的 ACI209、B4和CEB-FIP(1990)计算模型子程序得到的收缩应变和解析解基本吻合,徐变系数与解析解误差较小,在5%以内,符合工程要求。针对误差的出现,主要是徐变模型本构关系复杂,现成的规范模型,不可能完全反映混凝土的实际情况,且仍有较多问题有待解决,如构件截面尺寸影响的考虑,徐变模型公式中均将构件截面尺寸的影响放在收缩和徐变发展的时间函数中,程序已有考虑,加载前干燥情况的考虑,混凝土水灰比的考虑方法等[12],并且非线性分析也较容易存在计算迭代误差。因此,应通过对混凝土收缩徐变机理的理解和对其影响因素的研究来改进计算结果,加强对非线性徐变理论的研究,细化分析荷载步和收敛精度可进一步缩小误差,提高精度。
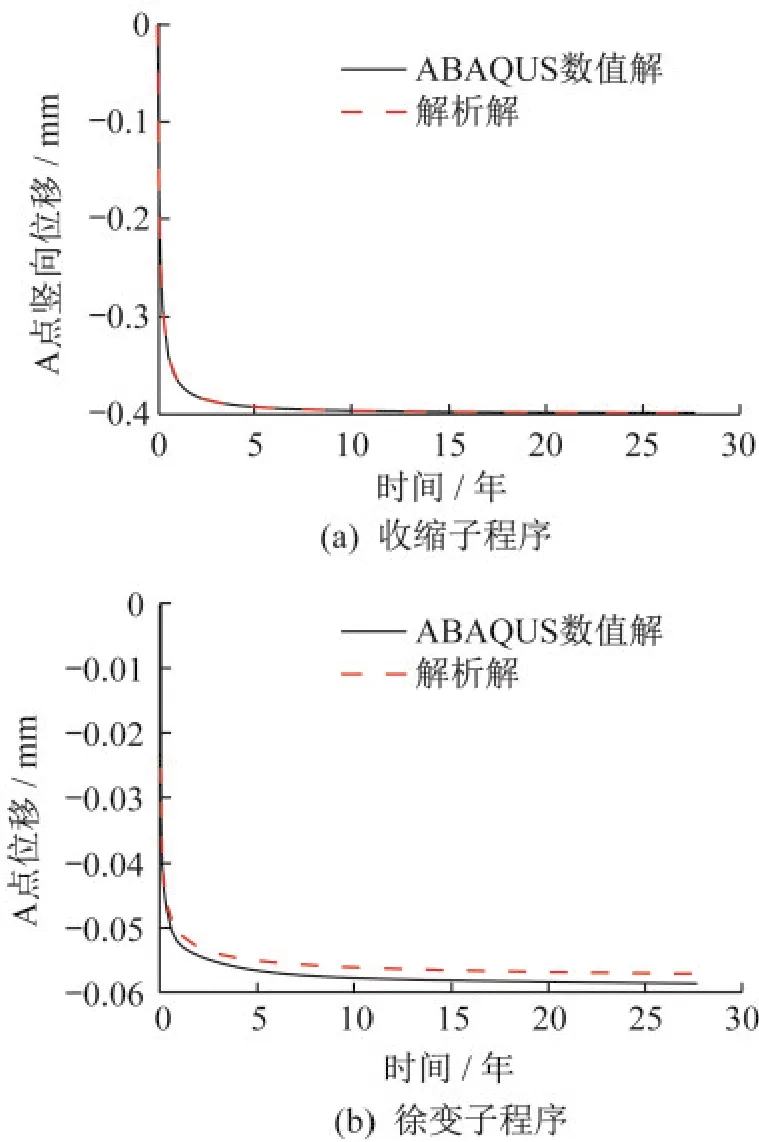
图5 ACI209收缩徐变子程序校核Fig.5 Checking of ACI209 shrinkage and creep subroutine

图6 CEB-FIP(1990)收缩徐变子程序校核Fig.6 Checking of CEB-FIP(1990)shrinkage and creep subroutine

图7 B4收缩徐变子程序校核Fig.7 Checking of B4 shrinkage and creep subroutine
3 算 例
某PC变截面梁桥跨径组合为(60+100+60)m,截面信息如图8所示,支座布置已知,中支墩采用盆式支座[13]。该桥悬臂浇筑共划分了14个节段,各节段腹板理论厚度与腹板厚度有关,与腹板高度无关,各底板理论厚度相差较大,由中墩向中跨跨中延伸,底板理论厚度逐渐减少,中墩附近节段底板理论厚度最大,其次是腹板,顶板理论厚度最小,如图9所示,各节段混凝土水灰比为0.39,环境湿度为70%,纵向有效预应力扣除摩擦损失和锚具回缩引起预应力损失。

图8 截面信息(单位:cm)Fig.8 Section information(Unit:cm)
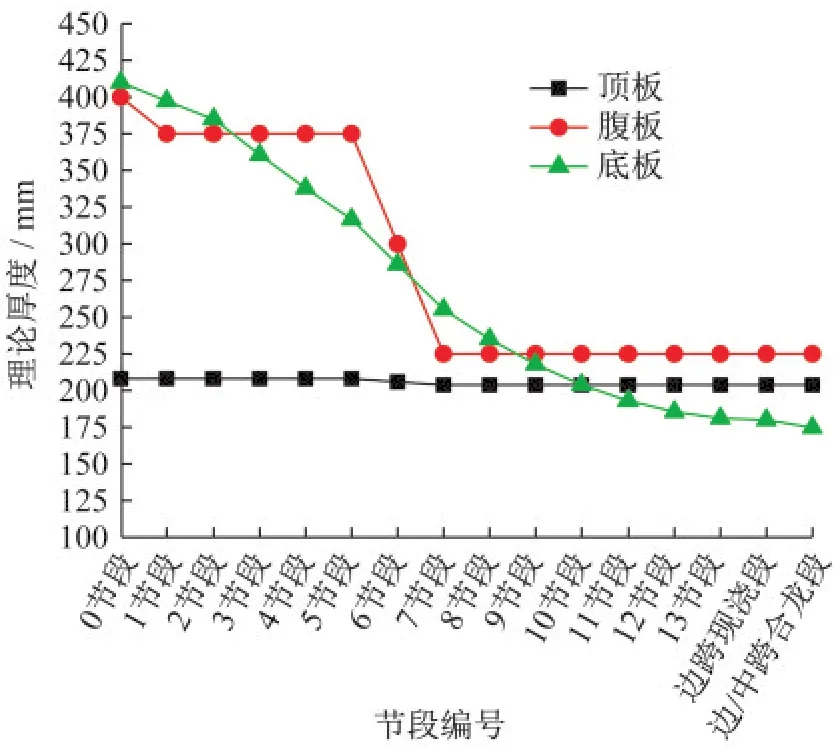
图9 各节段顶、底板和腹板理论厚度Fig.9 Theoretical thickness of top,bottom plate and web of each section
由于桥梁沿纵桥向预应力筋布置和结构对称,建立沿纵桥向1/2模型,三维实体元计算分析模型如图10所示。顶、底板及腹板理论厚度不同,赋予顶、底板及腹板不同收缩徐变发展曲线不同。

图10 三维实体元计算分析模型Fig.10 Three dimensional solid element calculation and analysis model
4 结构长期性能分析
4.1 长期预应力损失分析
三种收缩徐变模型下悬臂束、边跨合龙束和中跨合龙束预应力损失计算结果如图11所示。

图11 成桥后预应力损失分析Fig.11 Analysis of prestress loss after completion
由上可以看出:
(1)三种收缩徐变模型下,悬臂束、边跨合龙束和中跨合龙束预应力损失变化规律基本相似,均表现为预应力损失增长速率逐渐下降,其中ACI209模型在成桥第三年后预应力筋损失基本不再增长;CEB-FIP(1990)和B4模型预应力损失后期增长速率基本相同。
(2)相比其他两种收缩徐变模型,B4收缩徐变模型预应力损失最大,结构预应力损失与结构纵向位移相关。不同收缩徐变模型产生的预应力损失与边支座位移关系,如图12所示。

图12 边支座位移Fig.12 Displacement of side support
边支座位移均呈现前期增长速度快后期增长慢的变化趋势,B4模型对结构影响最大,CEB-FIP(1990)其次,ACI209模型影响最小。桥梁纵桥向受力类似于受压构件,边支座纵桥向位移与纵桥向收缩应变和徐变应变密切相关,不同收缩徐变模型下,支座位移的大小实际可以反映收缩徐变模型对结构作用的强弱。
4.2 结构挠度与应力长期效应分析
ACI209、CEB-FIP(1990)和B4三种混凝土收缩徐变模型下结构长期效应如图13、图14所示。

图13 不同收缩徐变模型下跨中挠度变化Fig.13 Variation of mid span deflection under different shrinkage and creep models
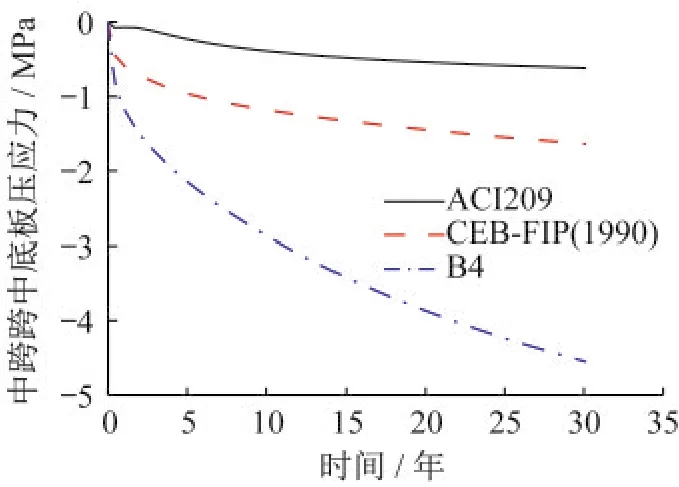
图14 跨中底板压应力变化Fig.14 Variation of compressive stress of mid span bottom plate
由上可以得到:
(1)不同收缩徐变模型下,跨中挠度变化规律不同。跨中挠度、收缩徐变模型收缩应变引起的预应力损失均和混凝土徐变作用强弱相关。
(2)三种收缩徐变模型下,底板压应力均减小。B4模型相对于ACI209和CEB-FIP(1990)对底板压应力减少量较大,且趋于不收敛的状态。
4.3 腹板主拉应力长期效应分析
采用三维实体元模型可以分析腹板主拉应力,结果如图15所示。

图15 在不同竖向预应力损失的截面重心处腹板主拉应力随时间变化Fig.15 Variation of web principal tensile stress with time at the section center of gravity with different vertical prestress loss
可以看出:
(1)中跨1/4~1/2区域相对于其它区域,腹板主拉应力对竖向预应力损失较为敏感。竖向预应力损失由50%增加至100%,中墩至中跨1/4区域内腹板主拉应力变化不大(应力云图颜色均在深蓝色附近),中跨1/4至中跨1/2区域腹板主拉应力变化较大,增加了0.5 MPa左右,由原来只在靠近下加腋处腹板存在主拉应力,扩算至该区域整个腹板。
(2)竖向预应力损失比例增大时,除中跨1/8截面重心处腹板主拉应力变化速率有所增大外,对其他几个截面重心处腹板主拉应力变化速度影响都较小。
5 截面应力状态与长期性能关联性分析
东南大学刘钊等[14]基于荷载效应平衡原理提出合理成桥状态概念,通过合理配置纵向预应力筋束适度平衡多种荷载效应,使结构处于合理成桥状态,达到抑制结构长期下挠的目的。中墩附近截面成桥应力状态与悬臂束配置有关,中跨跨中截面成桥应力状态与中跨合龙束配置有关。通过合理配置悬臂束和中跨合龙束使结构处于合理成桥应力状态,可以达到抑制结构长期下挠的目的。将悬臂束和中跨合龙束有效预应力分别增加50%和减少50%,分析截面应力状态对结构长期挠度的影响。不同悬臂束/合龙束有效预应力情况下,顶、底板压应力差和中跨跨中挠度随时间变化分别如图16、图17所示(压应力为负,拉应力为负)。
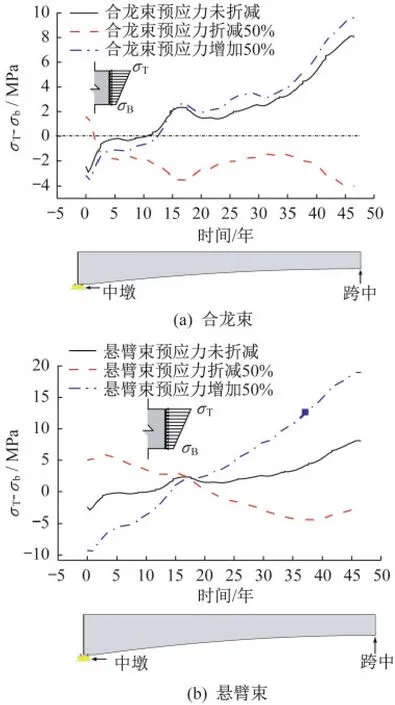
图16 不同预应力筋有效应力折减系数情况下中跨顶底板压应力差Fig.16 Pressure stress difference of middle span top and bottom plate in different effective stress reduction coefficients of prestressed tendons
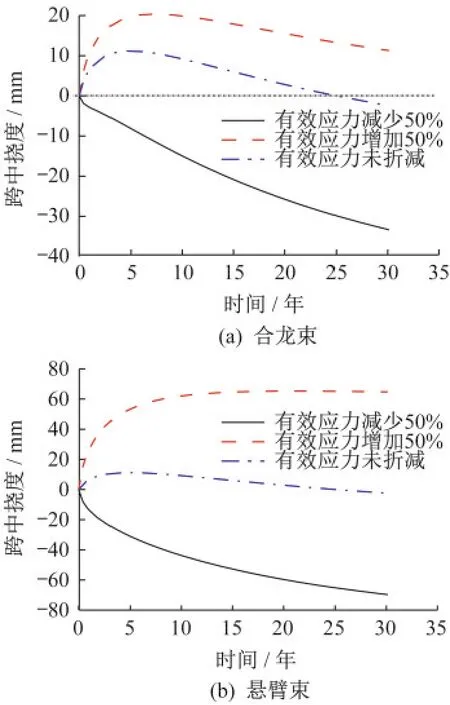
图17 不同预应力筋有效应力折减系数情况下中跨跨中挠度随时间变化Fig.17 Variation of mid span deflection with time in different effective stress reduction coefficients of prestressed tendons
由上分析可知:
(1)结构越偏向合理成桥状态,越有利于抑制结构长期下挠,即跨中截面顶、底板压应力差值越大和中墩墩顶、墩底截面压应力差值越小,越有利于结构抑制长期下挠。当悬臂束和中跨合龙束有效预应力分别减少50%时,结构偏离合理成桥状态,跨中挠度呈现不断发展的趋势。
(2)相比增加合龙束,增加悬臂束更加有利于抑制结构长期下挠。悬臂束和中跨合龙束有效应力增加50%时,通过比较中墩和中跨跨中截面顶、底压应力差绝对值及跨中挠度可以看出,增加悬臂束相比增加中跨合龙束可使结构更加偏向合理成桥状态,成桥30年中跨跨中挠度分别上拱了60 mm和11 mm。
综上分析,混凝土收缩徐变作用引起结构挠度和应力变化,是混凝土收缩徐变引起预应力损失和徐变作用共同作用、相互耦合的结果。沿结构纵桥向,混凝土收缩徐变对PC变截面梁桥的作用类似于受压柱,在预应力筋轴向压力作用下,结构纵桥向长度会缩短,引起预应力损失,造成跨中下挠,中跨底板压应力减少。混凝土徐变作用与结构成桥应力状态有关,满足合理成桥状态时,徐变作用下跨中将会上拱;结构偏离合理成桥状态时,徐变作用下跨中将会下挠。
6 结 论
通过Fortran语言编辑相应收缩徐变子程序,实现了ABAQUS三维实体元分析PC变截面梁桥在不同收缩徐变模型下结构挠度和应力长期效应,主要结论如下:
(1)桥梁设计时应充分考虑和对比分析运营期在不同收缩徐变模式下结构内力、长期挠度响应。
(2)应充分考虑中跨1/4~1/2区域内竖向预应力筋合理布置和施工保证措施,减少预应力损失,可有效减少和抑制长期效应斜拉裂缝开展。
(3)收缩徐变作用下各节段腹板主拉应力趋于均匀化,对于已经出现腹板斜裂缝,桥梁应采取相应措施,防止出现弥散性裂缝。
(4)进行PC梁桥设计时不仅需要考虑结构正常使用和极限承载力状态满足要求,还要保证截面处于合理成桥状态。
(5)影响实桥混凝土收缩徐变因素较多,本文未能完全模拟实桥的混凝土收缩徐变发展,并分析其对结构长期效应的影响,因此并不能完全反映算例桥梁的长期下挠行为。进一步研究可从桥梁施工开始,掌握混凝土基本参数,并在同等条件下开展收缩徐变试验以获取实桥的收缩徐变本构关系,同时开展实体元仿真分析,为桥梁长期效应分析提供依据。
