自适应整形正则化迭代最小二乘谱反演方法

乐友喜, 陈艺都, 吴佳伟, 曾 勉, 陈学国

(1.山东省深层油气重点实验室(中国石油大学(华东)),山东青岛 266580; 2.中国石油化工股份有限公司西南油气分公司采气四厂,重庆 402160; 3.中国石化胜利油田分公司勘探开发研究院,山东东营 257015)

基于反演的谱分析方法是一类新兴的时频分析方法[1-3]。该类方法从一般正问题出发,利用迭代反演的思想,直接反演求得信号的频谱分布。Portniaguine[1]分析了基于L1范数、L2范数及离散脉冲的反演谱分解方法,认为3种方法各自描述了地震信号不同尺度的信息;韩利[4]介绍了一种基于L1范数约束的稀疏反演谱分解方法,获得了信号的稀疏解;石战战等[5]研究了基于L1-L1范数稀疏表示的地震反演方法;王彦飞等[6]研究了地震时频分析的加权L1范数稀疏正则化及交替方向乘子算法;高秋菊等[7]采用L1范数正则化的L2范数作为稀疏约束反演谱分解的目标函数,并通过迭代阈值算法求解稀疏反问题;Puryear等[8]在前人的基础上研究了基于L2范数约束的反演谱分解方法,即最小二乘约束反演谱分解方法(CLSSA)。刘炳杨等[9]将Puryear提出的反演方法应用到辫状河道及储层描述中,取得了不错的应用效果;曾勉[10]研究了基于整形正则化的迭代反演谱分解方法,并应用到含气储层的谱分析中;另外,整形正则化方法在一维数据插值、速度估计、局部地震属性估计等领域取得不错的应用效果[11-14]。笔者在L2范数约束反演的基础上提出自适应整形正则化迭代最小二乘谱反演方法(ILSSI-ASR),同时,考虑到反演类时频分析方法的特殊性,构造一种自适应的整形算子(ASO),通过L曲线进行正则化参数的自动优选,以提高算法的收敛速度及频谱曲线的收敛速率。

1 方法原理

1.1 整形正则化理论

整形正则化理论首先由Fomel提出并将其扩展到非线性的反演问题中,为整形正则化在反演问题中的应用奠定了基础[11-13]。在Fomel看来,通常使用的Tikhonov正则化方法要求正则化算子项与目标项的L2范数同时达到最小,会显著降低反演算法的收敛速度;同时,经验化的正则化算子选取也减弱了算法的可适应性。针对这些问题,Fomel考虑了整形算子在控制预测模型形状等方面的作用后提出了整形正则化的方法。

傅里叶分析是在基函数空间中求信号的傅里叶系数,基函数为正弦和余弦波,在周期内基函数是正交的[16-17]。所求的傅里叶系数为信号在基函数空间的最佳逼近系数,即所求解的傅里叶系数{ck}满足:

exp(i2πfmt)>=0,k≠m.

(1)

式中,‖·‖2表示L2范数;f(t)为时间域的地震信号;ck为傅里叶系数;exp(i2πfkt)为基函数。

短时傅里叶变换首先利用窗函数截取部分信号,其他部分补零,然后进行傅里叶分析。短时傅里叶变换受窗函数的影响,往往会产生泄频和拖尾效应[18]。

Puryear等[8]提出了基于L2范数约束的反演谱分解方法,即最小二乘约束反演谱分解方法。

首先将正问题表述为

Lm=d.

(2)

式中,L为由正弦基构成的核矩阵,第k列(k=1, 2,…,N)为频率为kΔf的谐波,L(n,k)=cos(2πnΔtkΔf)+isin(2πnΔtkΔf),列数为频率的取值范围,第n行对应于时窗内的相对时间nΔt,行数与窗函数具有同样长度;d为用窗函数截取的地震信号;m为地震信号的频谱。

式(2)可进一步表述为

d(t)=c0ψ1(t)+c1ψ1(t)+…+cNψN(t).

(3)

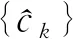
移动窗函数到下一个时刻,继续上述方法可获得信号在下一个时刻的频谱,重复以上步骤即可实现地震信号的谱反演。

上述问题的求解可表述为一个最小二乘问题:

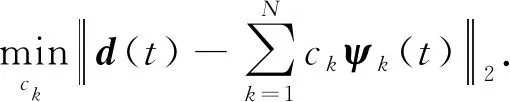
(4)

针对反演过程中可能存在的解的不唯一等问题,Tikhonov[19]引入正则化算子D与正则化参数ε,于是式(4)变形为如下形式:

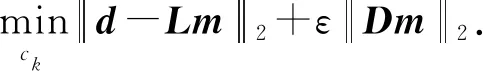
(5)

其代价函数可写为

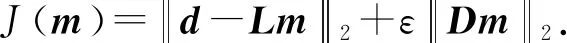
(6)

对式(6)求导,可得

(7)

从而得到方程组:

(LHL+εDHD)m=LHd.

(8)

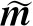
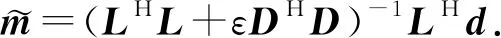
(9)

式中,LH为厄米特共轭矩阵。

在Fomel提出的整形正则化方法中,通过引入整形算子S来解决反演问题的不适定问题,具体表示为

S=(I+εDHD)-1.

(10)

由式(10)可得

εDHD=S-1-I.

(11)

将式(11)代入式(9),可得

(12)

式中,ε为正则化参数,主要控制反演算子的相对尺度;S为整形算子,通常可选择Gaussian算子,起到控制预测模型的形状的作用。

1.2 基于自适应整形正则化的迭代谱反演

为提高谱反演算法的收敛性和稳定性,借鉴Puryear的思路[2],引入模型权重Wmi(初始值为单位矩阵)和数据权重Wd加以约束。这里,模型权重会随着迭代的进行而变化,数据权重只与时窗所截取的数据有关,与迭代次数无关。引入权重矩阵后,式(2)可写为

Lwimwi=Wdd.

(13)

其中

式中,i为迭代的次数。

引入正则化算子,采用迭代最小二乘优化方法求解反问题(5)的目标函数变为

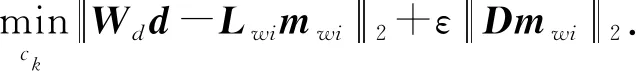
(14)

利用式(14)便可求得mwi的值：

mwi=[I+Si(LwiHLwi-I)]-1SiLwiHWdd.

(15)

式中，Si为第i次迭代的整形算子。

第i次迭代获得的信号频谱为

mi=Wmimwi.

(16)

在迭代的过程中，模型权重逐次更新：

Wm(i+1)=diag(abs(mi)).

(17)

式中，diag( )函数用于构造一个对角矩阵，不在对角线上的元素全为0。

迭代运算进行时整形算子Si对预测模型的形状起着关键的控制作用,因而其选取是否合适是决定着反演结果能否接近真实情况的十分重要的因素[20-21]。针对反演谱分解方法的特点构造出一种自适应整形正则化算子(adaptive shaping operator, ASO):选取归一化的第i次迭代的信号频谱Reg(mi)作为i+1次迭代的整形算子Si+1,即

Si+1=Reg(mi).

(18)

式中,Reg(mi)代表对第i次迭代的信号频谱mi的归一化处理。

归一化后的频谱Reg(mi)只保留了此次迭代的频谱曲线的趋势特征,将其作为下次迭代的整形算子可充分发挥整形算子在控制预测模型形状方面的优势,达到加速收敛速度、提高反演准确度的效果。

对主频为30 Hz的雷克子波进行分析处理,以验证自适应整形算子的性能。图1(a)为主频为30 Hz的雷克子波,图1(b)为利用不同期望的Gaussian算子和自适应整形算子(ASO)处理该雷克子波获得的频谱曲线,Gaussian算子对应的是特征对称的钟形曲线,具体表达式如下:

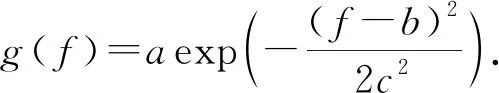
(19)

式中,a为Gaussian曲线尖峰的高度;b为尖峰的坐标,用于频谱整形时对应的就是频率坐标;c为标准方差,表征钟形曲线的宽度。

由图1可知,期望值对于采用Gaussian算子的时频处理结果有较大的影响:当Gaussian算子对应期望值接近子波主频时,其频谱曲线才能与真实结果有较高拟合度;而当期望值与主频相差较大时,所获谱线与真实结果有较大的差距。但是,自适应整形算子无需已知子波主频便可获得与真实频谱曲线拟合度较高的频谱曲线。地震波作为一种典型的非平稳信号,事先难以获得与频谱曲线有关的信息。因而自适应整形算子相比于通常使用的Gaussian算子在频谱准确度方面有优势。

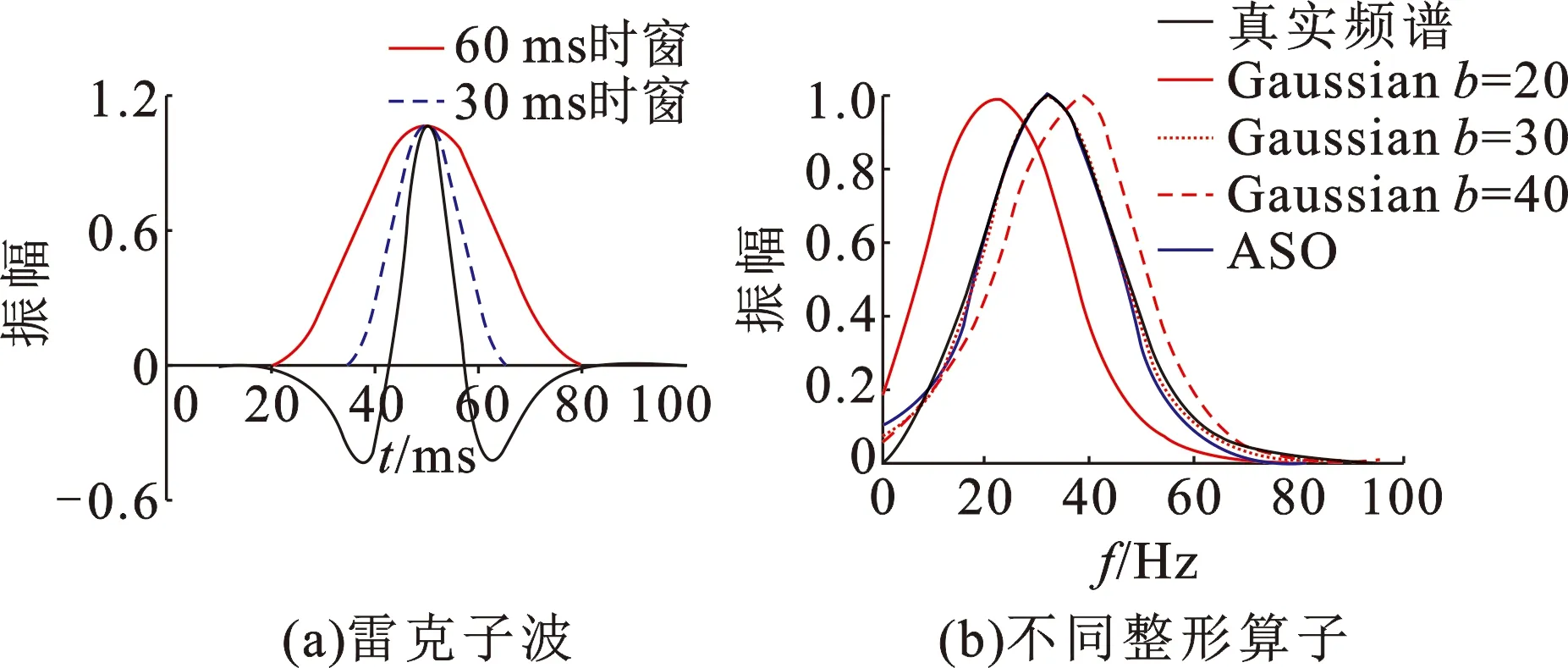
图1 雷克子波频谱分析

1.3 正则化参数的自动优选

正则化参数ε对正则化效果有较大的影响,前人的研究中ε一般取为常数,这样虽对模型进行了正则化处理,却得不到最优结果。式(14)中第一项为偏差函数,要求谱反演结果忠实于原始地震信号所包含的信息,但过分依赖第一项会放大噪音,使谱反演结果信噪比变差,时频谱图像模糊不清;第二项为正则化函数,强调时频谱图像的光滑性,能抑制噪音成分,但过分依赖会丢失时频谱图像的边界等细节信息,从而导致时频谱的失真。适当的正则化参数ε能使偏差函数和正则化函数保持一定的平衡关系,因此正则化参数的自动优选是极其重要的[22-23]。

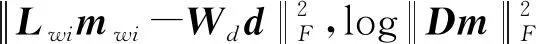
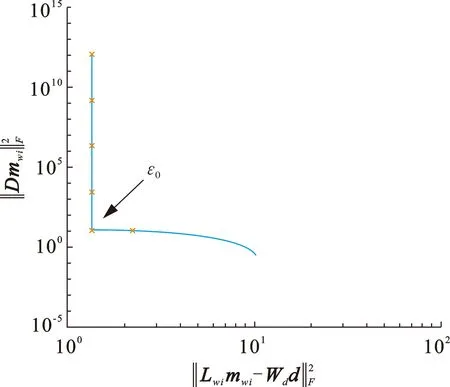
图2 第一次迭代的L曲线

为了求得L曲线拐角点的参数值,通常引入曲率,曲率最大时则对应此处的值[24]。曲率表达式一般为

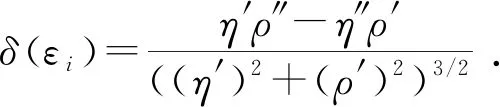
(20)

其中

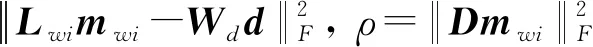
式中,εi为i次迭代所对应的正则化参数变量;δ为相应的曲率函数;η′、ρ′、η″、ρ″分别表示一阶、二阶导数。

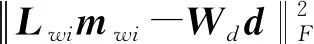
对于正则化参数选取,理想的效果应为每次循环都会利用L曲线法求取ε值,但L曲线计算需要先对式(14)进行谱反演求解,影响计算效率,所以需要进一步改进算法,将整个过程插入若干个控制节点,每一次迭代求解时的正则化参数估算值经数值拟合得到:

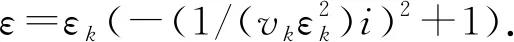
(21)

式中,k为分段优选正则化参数的控制节点序号;εk、vk为调节系数(εk、vk>0);ε0为通过L曲线求取的第一次迭代的ε值;v0为给定的初始值。

调节系数vk和εk通过梯度下降法求得,对应的损失函数为

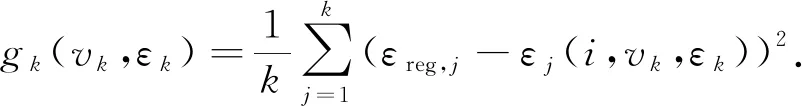
(22)

式中,εj(i,vk,εk)为由式(21)定义的关于迭代次数i和调节系数vk和εk的函数;j(j≤k)为计算ε时所对应的控制节点;εreg,j为通过L曲线计算得到的控制节点j处的目标值。只需要设置合适的学习率α和最小误差,通过不断迭代,调节系数修正公式收敛时即可估计出调节系数vk和εk。修正公式为

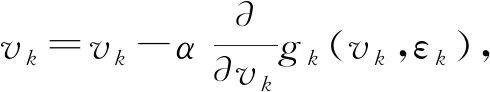
(23)

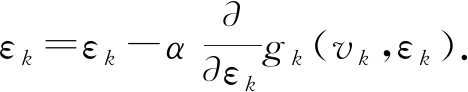
(24)

为了验证该方法的谱反演效果,将短时傅里叶变换(STFT)、最小二乘约束反演谱分解方法(CLSSA)、正则化参数ε取固定值的ILSSI-ASR方法以及ε自动优选的ILSSI-ASR方法分别作用于30 Hz Ricker子波,并用较窄的Hanning窗函数(30 ms)截取,其反演结果如图3(a)所示,图中黑色线为30 Hz雷克子波的真实频谱;青色线为STFT分析得到的频谱;红色点线为CLSSA反演得到的频谱;蓝色虚线和棕色点划线分别为ε取固定值和ε自动优选的ILSSI-ASR方法反演得到的频谱。从图中可以看出:当采用较窄的时窗截取时间信号进行谱分析时,STFT方法不能反映原始时间的频谱特征,短时窗截断后增强了虚假的低频信号;CLSSA和ILSSI-ASR方法都可以得到较为准确的结果,对比低频端和高频端局部放大后的结果(图3(b)和 (c)),CLSSA方法的高频信息存在一定的误差;ILSSI-ASR方法由于引入了自适应整形正则化算子,会使得谱图上的能量团向信号真实频率方向聚集,但由于ε是取固定值,如果ε取值过大或过小,都会使反演结果变差,从而不能得到最佳的反演效果,对于小于15 Hz的低频成分以及大于50 Hz的高频成分,与真实频谱存在较为明显的偏差;如果根据正则化参数自动优选取值时,随着每次迭代,其值是相应自动调整的,此时在时频谱的低频端稳定、能量聚集性好,与真实频谱吻合度高,因此反演结果达到了最佳。

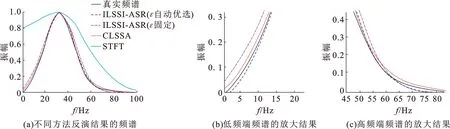
图3 不同方法作用于30 Hz Ricker子波的反演结果

2 模型测试及实例分析

利用本文方法对模型信号进行了测试。图4(a)为频率呈二次型增长的Chirp信号模型,分别采用CLSSA方法和本文方法经谱反演处理获得的时频谱如图4(b)、(c)所示。相比于CLSSA方法,本文方法的反演结果与已知的Chirp信号时频关系曲线(图中的黑色虚线)吻合程度很高,拥有很高的频率分辨率,尤其对于信号的高频成分,它在分辨率方面的优势更为明显。因而该方法对于信号的不同频率成分均保持有较高的时频分辨率。

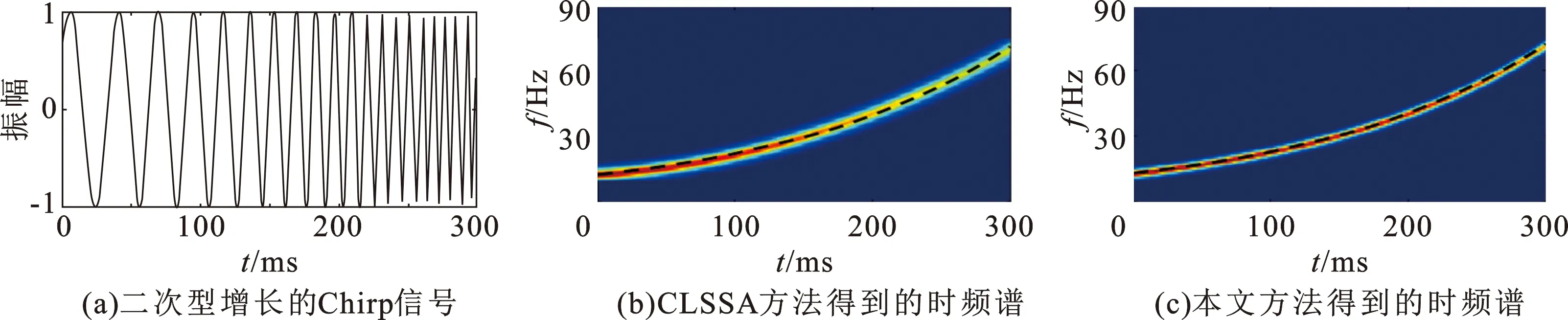
图4 反演得到的Chirp信号的时频谱

图5(a)为频率随时间变化的复杂信号,分别采用CLSSA方法和本文方法经谱反演处理获得的时频谱如图5(b)、(c)所示。观察发现,本文方法的反演结果完全与已知的模型信号时频关系曲线(图中的黑色虚线)吻合程度很好,谱图上能量分布均匀、变化连续;尤其在突变部位(250 ms),能谱分布清晰,可准确识别突变发生的部位。综合以上模型测试结果,可以得出以下结论:本方法获得的时频谱能量分布更为均匀,同时拥有更好的频率分辨率,可准确获得信号频率随时间的分布特征。

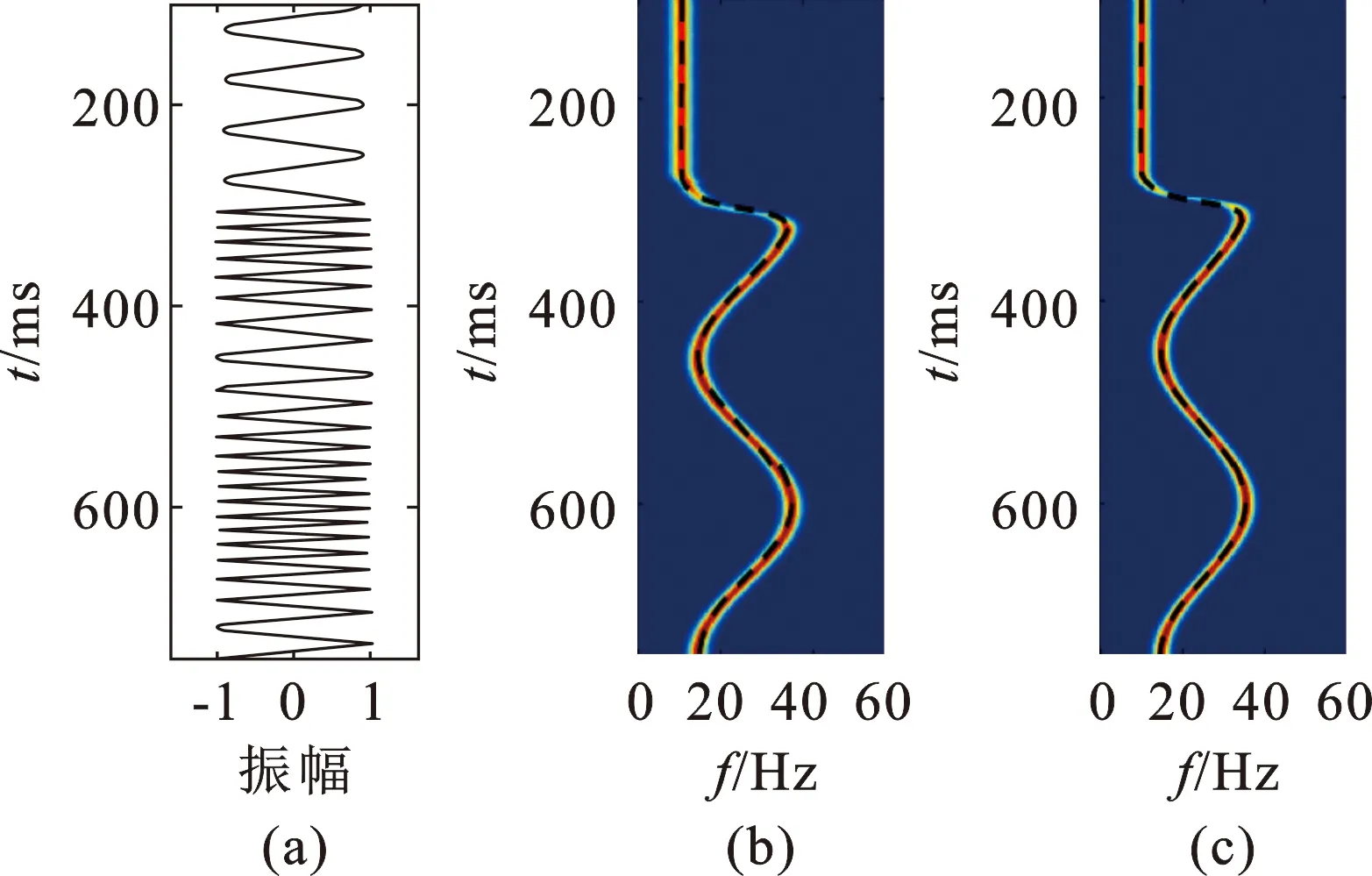
图5 反演得到的复杂信号的时频谱

接下来,考察该方法对于如图6(a)所示的合成地震记录的时频谱分解能力,该地震记录由4个主频为20 Hz的零相位雷克子波(图6(b))、两个主频为40 Hz(图6(c))的最小相位雷克子波(图6(d))以及两个主频为70 Hz的零相位雷克子波(图6(e))复合而成。图6(c)为采用CLSSA方法反演获得的时频谱,图6(f)、(g)分别为采用ILSSI-ASR方法时正则化参数ε取固定值0.1以及ε自动优选后反演获得的时频谱。从图中可以看出:ILSSI-ASR方法相比于CLSSA方法,时频谱分辨率及能量聚集性更高,反演结果更加准确;但由于正则化参数ε对正则化效果有较大的影响,如果ε取固定值,则往往很难取得一个合适的固定值,该值过大或过小都不能得到最佳的反演效果,出现了一定程度的失真,尤其对于20 Hz的低频信号,畸变更为明显;如果根据正则化参数自动优选取值时,随着每次迭代,其值是相应自动调整的,此时在时频谱的低频端稳定、能量聚集性更好,反演结果达到了最佳。

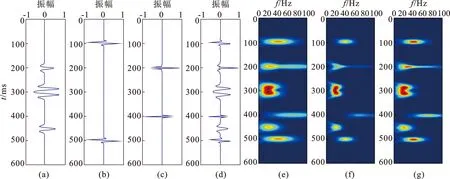
图6 不同方法对合成地震记录进行谱反演得到的时频谱

利用该方法分析了实际地震记录的时频分布特征。如图7(a)为研究区的一段地震剖面,经钻井资料证实,A井处存在一良好的含气储层(椭圆表示部位),气层上部存在一反射能量较强的煤层(箭头位置),对应井旁道数据如图7(b)所示。利用本文方法对该井旁地震道数据进行谱反演处理,得到的时频谱如图7(c)所示。观察发现,含气储层位于时频谱上的能量团最强的位置(红色箭头,时间2 670～2 695 ms),煤层在时频谱上的能量团也比较强(绿色箭头,时间2 130～2 170 ms),谱图上的能量团收敛,在频率方向上有近似“挤压”的效果。进一步分析表明,这种“挤压”效果与自适应整形算子(ASO)的引入相关,它使得谱图上的能量团向信号真实频率方向聚集,在一定程度上压制噪声的同时,获得了拥有更高频率分辨率的时频谱。

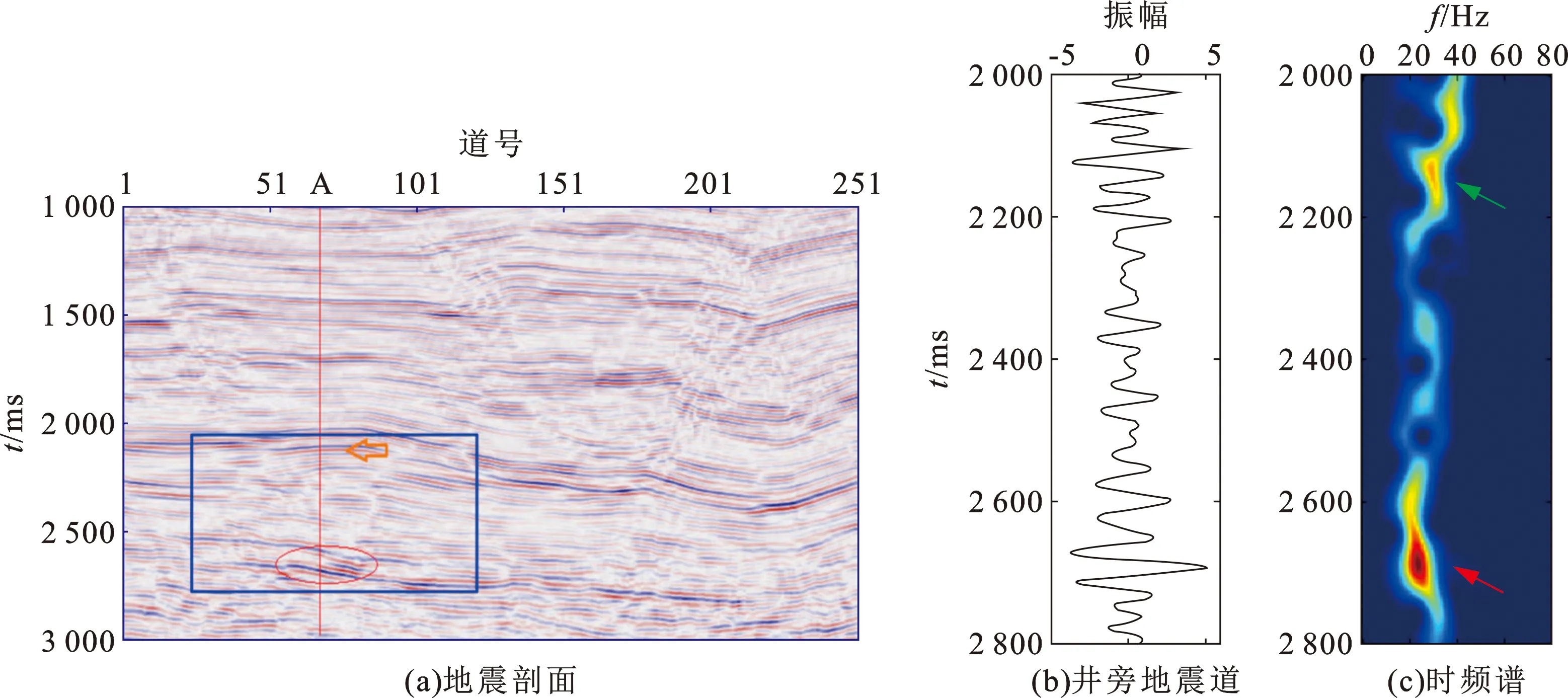
图7 井旁地震道及其时频谱

图8是利用本文方法对实际地震数据体经谱反演处理获得的不同频率的瞬时振幅剖面(对应于图8(a)方框中的范围),其中椭圆为含气储层所处的位置,箭头为煤层所处的位置。含气储层所对应的优势频带为25～35 Hz,在25 Hz剖面上能量最强,随着频率增加,能量衰减较为明显,达到40 Hz时已几乎完全衰减;煤层所对应的优势频带为30～40 Hz,由30 Hz增加到40 Hz,能量没有发生衰减。综上,本文方法有很好的时间分辨率及能量聚集性,可对含气储层进行更加精细的描述。

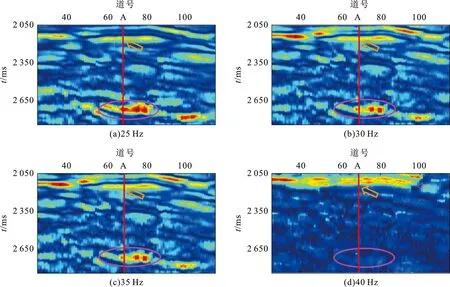
图8 经谱反演得到的不同频率的瞬时振幅剖面

3 结束语

针对反演算法中存在的问题,本文中采用整形正则化的方法加以约束;同时,构造了一种自适应的整形算子,并对正则化参数进行了自动优选,较好地解决了反演过程中遇到的多解性及稳定性等问题,获得了信号在时-频域的分布特征。实际应用结果表明,该方法对信号能量团有汇聚的作用,自适应算子的引入使得谱图上的能量团向信号真实频率方向聚集,在一定程度上压制噪声的同时,获得了拥有更高频率分辨率的时频谱,提高了该方法含气储层精确描述的能力。但是,该方法计算量大、对计算机性能有较高的要求,因而进一步提高算法运行速度是该方法未来研究的重要内容。