修正本征Bernstein-Durrmeyer型算子的逼近

张 斌，虞旦盛

(杭州师范大学数学学院，浙江 杭州 311121)

0 引言

1987年，Goodman等[1]引入了本征Bernstein-Durrmeyer型算子

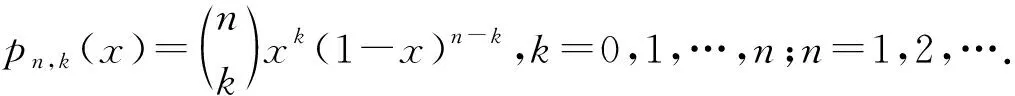
Un(f,x)相较于一般Bernstein-Durrmeyer型算子的优点是其保持线性函数，而普通Bernstein-Durrmeyer型算子并不保持线性函数.许多学者对Un(f,x)的逼近性质做了研究[2-14].在文献[4]中，Gonska等给出了Un(f,x)对闭区间上连续函数逼近的正定理与逆定理，结论如下:

定理1设0≤λ≤1为固定常数，则对任何f∈C[0,1]，存在一个仅依赖于λ的正常数C，使得

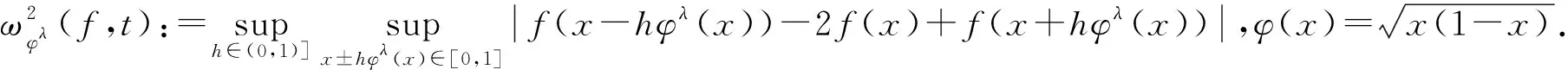
定理2设0≤λ≤1，则对任意f∈C[0,1]，θ∈(0,2)，以下条件等价：

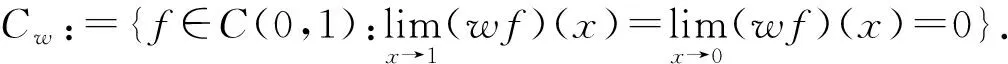
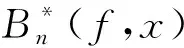
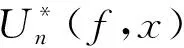
定理3设0≤λ≤1为固定常数，则对任何f∈C[0,1]，存在一个仅依赖于λ的正常数C，使得

我们还有下面的Voronovaskaja型估计：

定理4对任何f∈C2[0,1]，存在一个仅依赖于λ的正常数C，使得

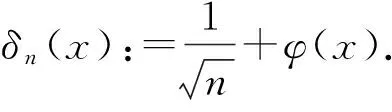
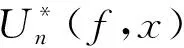
1 引理及其证明

为了证明上述定理，首先给出几个引理.

引理1[5]下列等式成立：

引理2下列等式成立：

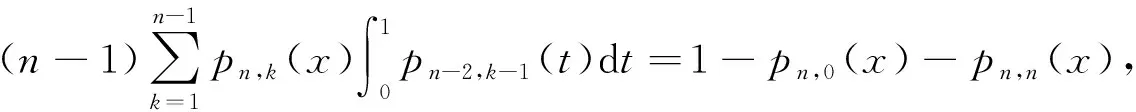
(1)

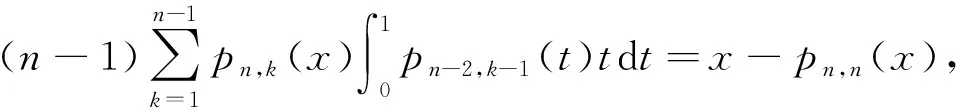
(2)

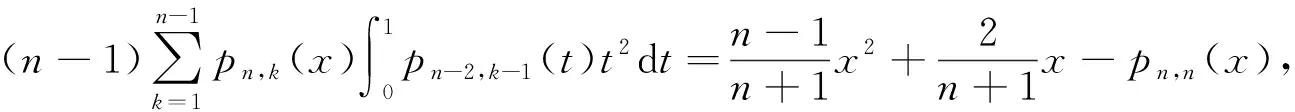
(3)

证明对k=1，2，…，有

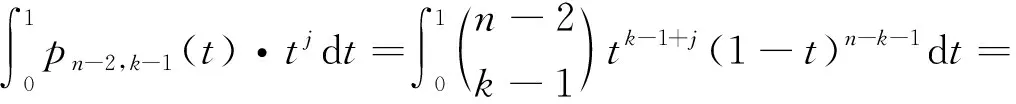
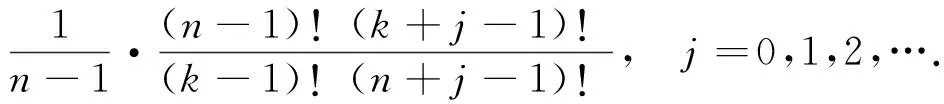
(4)

因此，结合引理1及式(4)，可立得(1)(2)及

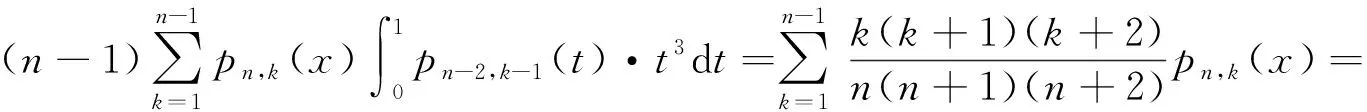
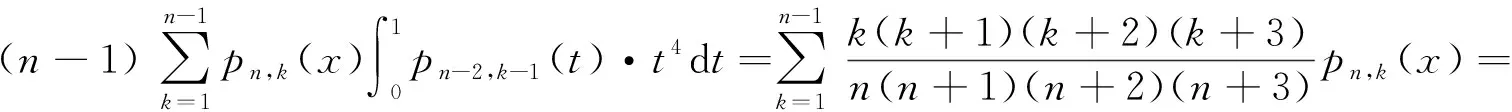
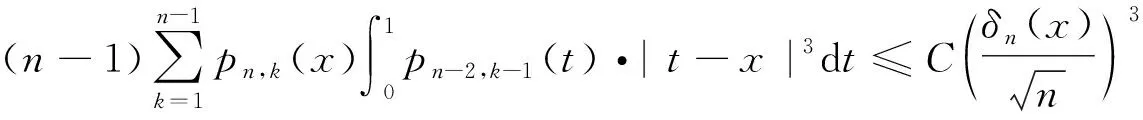
证明由引理2及Cauchy不等式可得

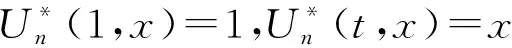
证明由式(1)、(2)可得

pn,0(x)+pn,n(x)+1-pn,0(x)-pn,n(x)=1;

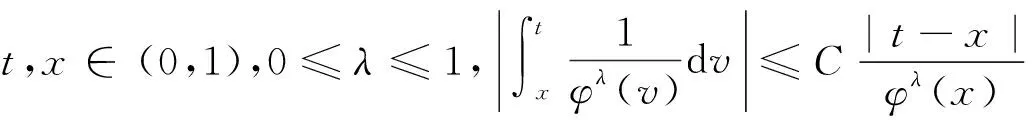
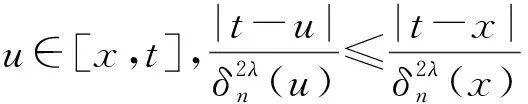
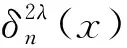
2 定理的证明

定理3的证明对任何f∈C[0,1]，定义K-泛函

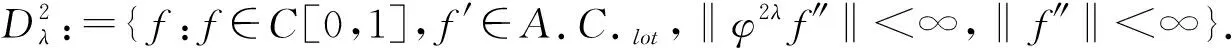
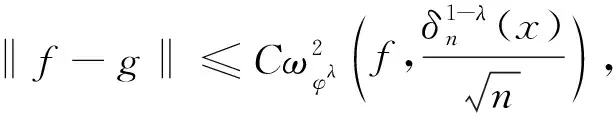
(5)

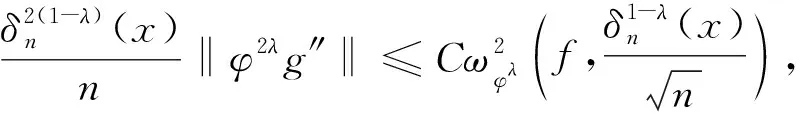
(6)

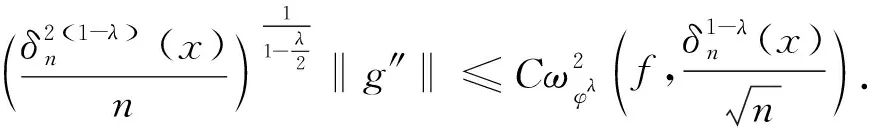
(7)

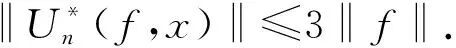
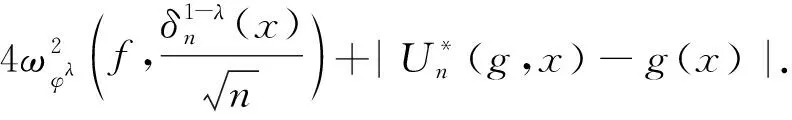
(8)

由Taylor展开式可得

因此利用引理4知

从而有

I1+I2+I3+I4+I5.

首先估计I1.结合引理2和引理6，有

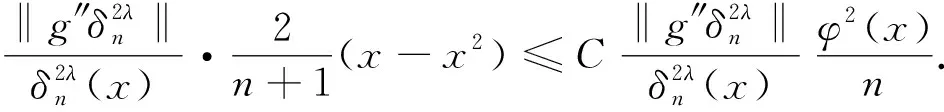
(9)

再来估计I2.再次应用引理6，有

类似地，可以得到

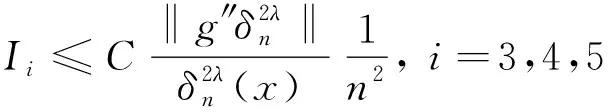
(11)

由式(9)— (11)，并结合式(6)、(7)，可得

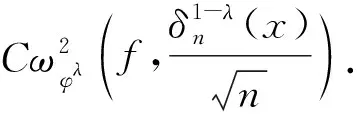
(12)

因此定理3得证.

定理4的证明对任何f∈C[0,1]，定义K-泛函:

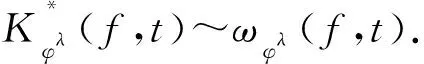
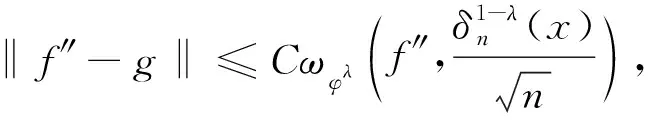
(13)

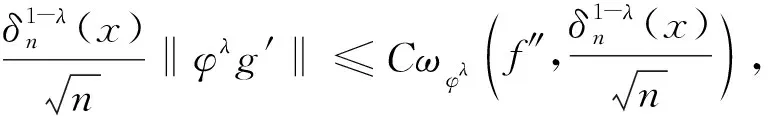
(14)

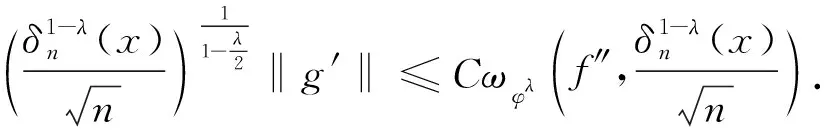
(15)

简单计算可得

因此，

M1+M2+M3+M4+M5.

先来估计M1.直接计算得

由式(1)-(3)及(13)得

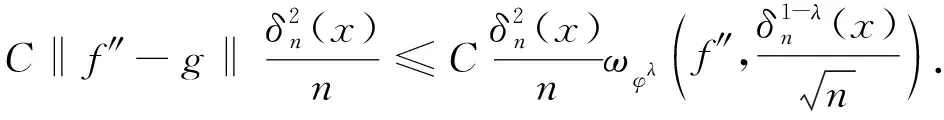
(16)

类似地，可得到

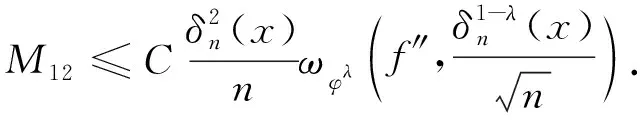
(17)

对于M13，有

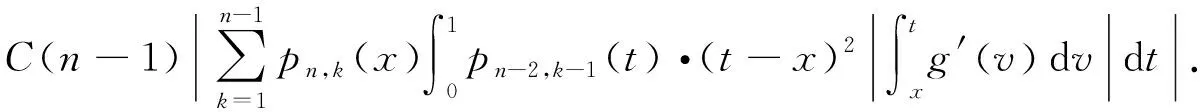
(18)

以下分两种情形对M13进行估计.

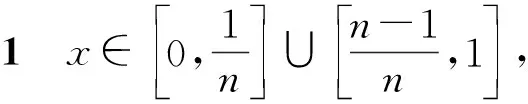
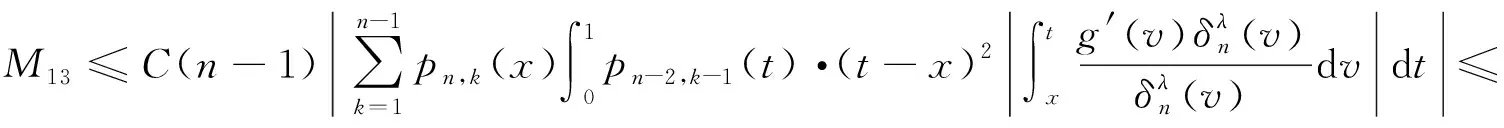
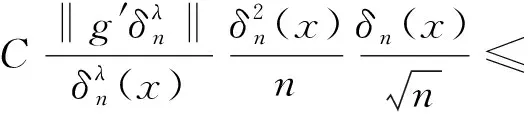
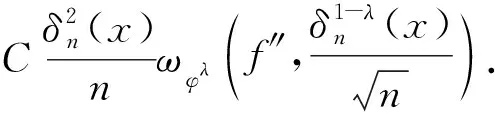
(19)

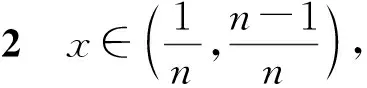
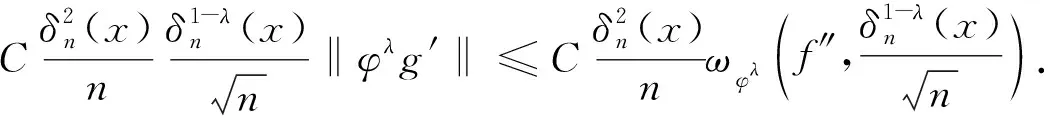
(20)

结合式(16)—(20)，得

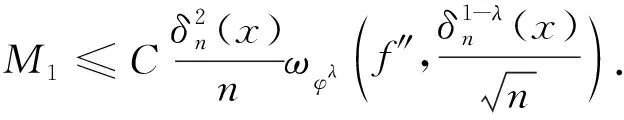
(21)

对于M2，有

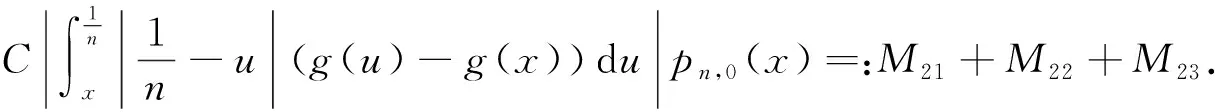
(22)

对于M21，结合式(13)有

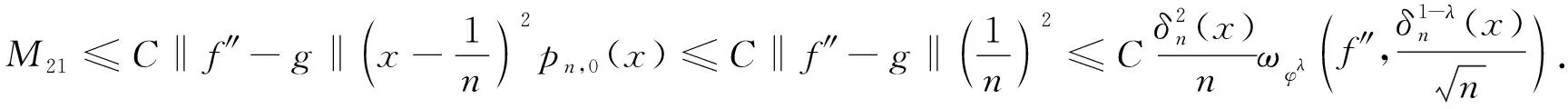
(23)

类似地可得到

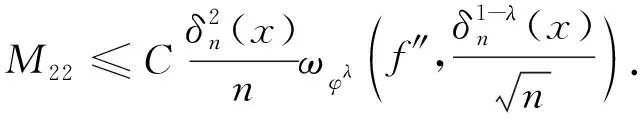
(24)

对于M23，类似于对式(18)的讨论，得

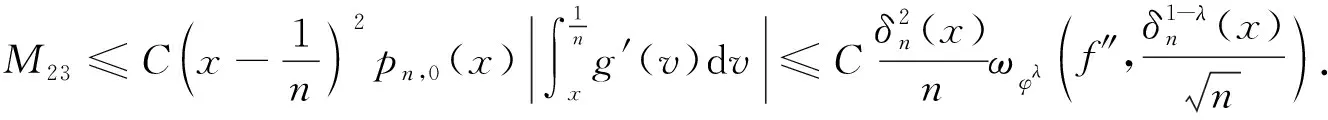
(25)

因此，结合式(23)—(25)，得

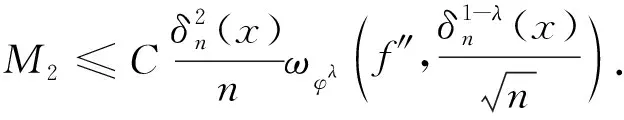
(26)

类似地，对于Mi,i=3,4,5，都有

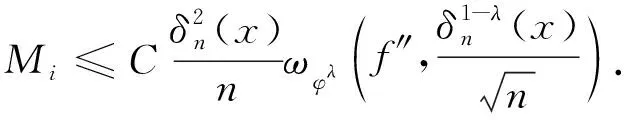
(27)

结合式(21)、(22)、(26)和(27)，定理4得证.