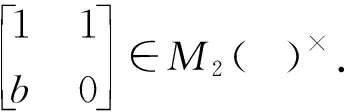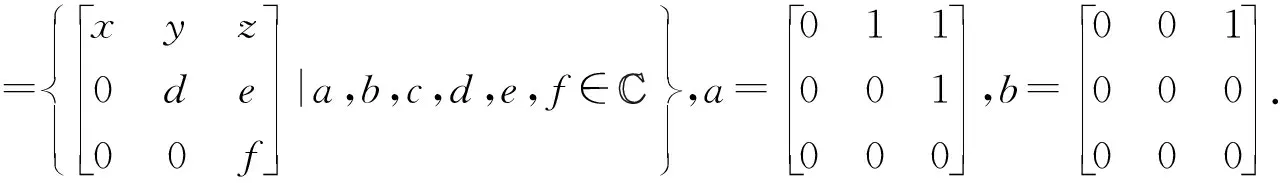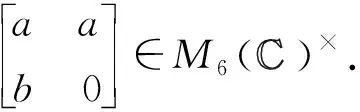关于p群逆的几个新特征

周心悦，方爱香，陈焕艮

(1. 杭州师范大学数学学院，浙江 杭州 311121； 2. 湖南文理学院数理学院，湖南 常德 415000)

0 引言

在本文中,我们研究 Banach 代数中元素a的p群逆.p群逆是介于群逆和p-Drazin逆之间的一种新的广义逆.p-Drazin逆推广自Drazin逆，在[1]中就有关于三角矩阵的Drazn逆以及元素和的Drazin逆相关探讨.对于群逆问题,已经有了很多研究,如矩阵的群逆[2-4]元素和或乘积的群逆[5-6],以及群逆与Drazin逆的关系等.p-Drazin逆在[7]中引入，而[8-9]给出了元素和与积有p-Drazin逆的条件.在本文中,我们进一步对p群逆进行研究，获得Banach代数中元素是p群可逆的新特征.

下文中，A代表着有单位元的Banach代数,J(A)是A的Jacobson根.A×代表A中的所有p群可逆元集合,而A-1则是A中的所有可逆元集合.

定义1对A中元素a，如果存在x∈A使得

ax=xa,xax=x,axa=a,

(1)

则称x是a的群逆,记作a#.

定义2设a∈A，如果存在x∈A使得

xa=ax,xax=x,a-a2x∈J(A),

(2)

则称x是a在A中的p群逆，记作a×.

本文第一节主要介绍了基本定义.第二节讨论了Banach代数中元素p群可逆的充要条件.第三节得到了Banach代数中p群逆和p-Drazin逆之间的关系.第四节我们研究了Banach代数上2×2矩阵的p群逆问题.

1 等价条件

这一节主要目的是得到a∈A×的一个新特征.

引理1令a∈A,下列条件等价:

(1)存在e2=e∈comm2(a)使得a-e∈J(A);

(2)a-a2∈J(A).

证明见[10].

定理1令a∈A,则下列条件等价:

(1)a∈A×;

(2)存在x∈A使得

ax=xa,a-a2x∈J(A).

(3)

证明(1)⟹(2)显然成立.

(2)⟹(1)根据假设,我们有x∈A使得

ax=xa,a-a2x∈J(A).

(4)

令z=xax.那么za=az.令e=1-za.于是

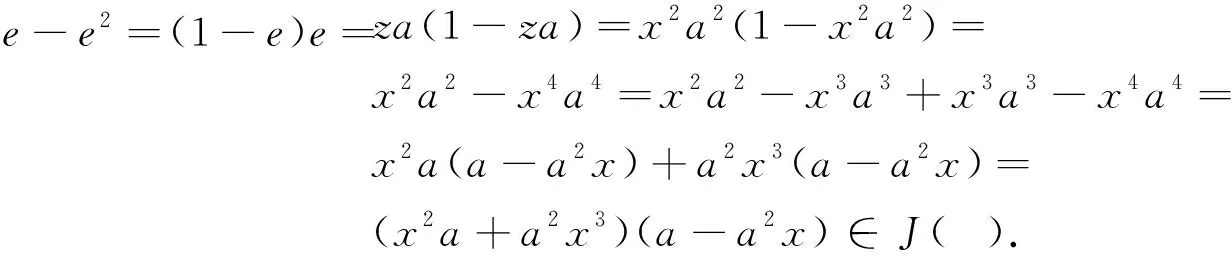
(5)

根据引理1,存在f2=f∈comm2(a)使得

e-f∈J(A).

(6)

此外,我们需验证a+f∈A-1且af∈J(A).

由于a+f=a+f-e+e=a+e+f-e,我们需证a+e∈A-1.

(a+e)(z+e)=1-a2x2+a4x4+a-a3x2+ax2-a3x4=

1-(a2x2-a3x3+a3x3-a4x4)+(a-a2x+a2x-a3x2)+

(ax2-a2x3+a2x3-a3x4)=

1-ax2(a-a2x)-a2x3(a-a2x)+(a-a2x)+ax(a-a2x)+

x2(a-a2x)+ax3(a-a2x)=

1+(1+ax+x2+ax3-ax2-a2x3)(a-a2x)∈A-1.

(7)

因此a+f∈A-1.由于af=a(f-e+e)=a(f-e)+ae.

我们只需证ae∈J(A).

ae=a-a3x2=a-a2x+a2x-a3x2=

a-a2x+ax(a-a2x)=(1+ax)(a-a2x)∈J(A).

(8)

由此可得a∈A×.

推论1令a∈A.则下列条件等价:

(1)a∈A×;

(2)存在f∈comm(a)使得a+f∈A-1且af∈J(A).

证明(1)⟹(2)显然.

(2)⟸(1)令x=(a+f)-1(1-f).由于f∈comm(a),我们有ax=xa.

验证

a-a2x=a(1-ax)=a(1-(a+f-f)(a+f)-1(1-f))=

a(1-(1-f(a+f)-1)(1-f))=a(f+f(a+f)-1(1-f))=

af(1+(a+f)-1(1-f))∈J(A).

(9)

根据定理1,a∈A×.

如果存在元素e∈A使得a+e∈J(A)且ae=ea则称元素a∈A是J-quasipolar的[11].

推论2一个Banach代数中的每个J-quasipolar元素都是p群可逆的.

证明令A是一个Banach代数且a∈A是J-quasipolar元素.那么存在e2=e∈comm(a)使得

a+e∈J(A).

令r=a+e.那么由于(1-2e)2=1,可得a(1-e)=(a+e)(1-e)∈J(A),a+(1-e)=r+(1-2e)=(1-2e)(1+(1-2e)r)∈A-1.根据推论1,a是p群可逆的.

推论3令a∈A且满足a-a2∈J(A),那么a有p群逆.

证明令x=1∈A.那么a-a2x∈J(A),ax=a=xa.根据定理1,我们有a∈A×.

定理2令a∈A,则下列条件等价:

(1)a∈A×.

(2)存在p2=p,x∈A使得1-p=ax=xa且ap∈J(A).

证明(1)⟹(2)令p=1-aa×,那么p2=p,1-p=aa×=a×a∈aA∩Aa以及ap=a-a2a×∈J(A).

(1)⟸(2)根据假设,ax=xa,p=1-ax=1-xa,可得a-a2x∈J(A).

根据定理1,a∈A×.

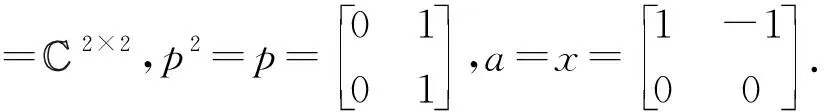
例2令V是上的一个无限维向量空间,A=End(V).易知A是VN正则环，从而J(A)=0.记{x1,x2,…,xn…}是V的一组基.

定义

σ(xi)=xi+1对于所有i∈,(10)

τ(x1)=0,τ(xi)=xi-1对于所有i≥2.(11)

令a=σ,x=τ.那么a,x∈A且ax=1,xa≠1.令p=0.

那么1-p=ax,ax≠xa以及ap=0.此外,可验证a不属于A×.

如果a∈A×,则a有群逆.有a=aa#a.那么ax=aa#ax也就是说aa#=1,a#a=aa#=1.因此a可逆,矛盾.

2 p-Drazin逆

元素a∈A称为p-Drazin可逆,即存在x∈A和整数k≥1满足

ax=xa,xax=x,ak-ak+1x∈J(A).

(12)

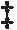
本节我们将刻画p群逆和p-Drazin逆之间的关系.

定理3令a∈A,则下列条件等价:

(1)a∈AP.

(2)存在某个n∈,使得an∈A×.

证明(1)⟹(2)由于a∈AP.那么存在x使得ax=xa,x=xax,an-an+1x∈J(A).所以我们有

anxn=xnan,an-(an)2xn=an-an+1x∈J(A).

根据定理1,an∈A×.

(1)⟸(2)an∈A×.所以我们有an-a2n(an)×∈J(A).这里an-a2n(an)×=an-an+1(an-1(an)×)∈J(A).可验证(an-1(an)×)a(an-1(an)×)=(an-1(an)×)且a(an-1(an)×)=(an-1(an)×)a,这意味着a∈AP.

推论4令a∈A.那么a∈AP当且仅当存在x∈A使得ax=xa,an-an+1x∈J(A).

证明⟹显然.

⟸根据假设,存在x∈A使得ax=xa且

an-(an)2xn=(an-an+1x)+(an+1x-an+2x2)+…+(a2n-1xn-1-a2nxn)∈J(A),

anxn=xnan.且an∈A×.根据定理3,a∈AP.

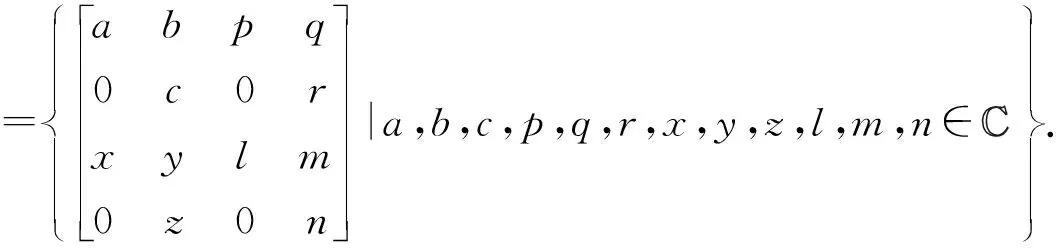
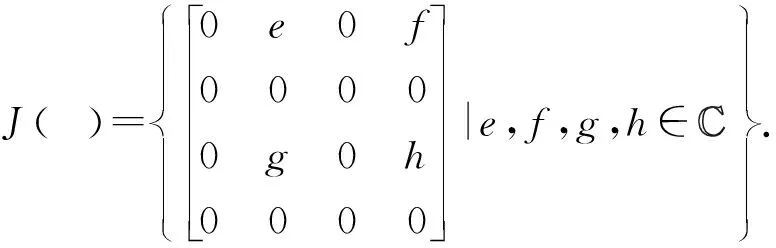
那么a2=0∈A×,又a∉A×.根据定理3,a∈AP.

引理2令a∈A.则下列条件等价:

(1)a∈A×;

(2)a∈AP和aaπ∈J(A).

定理4令a,b∈A×.如果a2b=aba且b2a=bab,那么a+b∈A×当且仅当1+a×b∈A×.

(13)

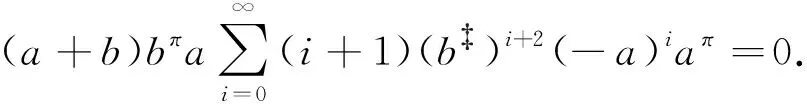
根据[9，定理2.10]证明的第三步,我们有

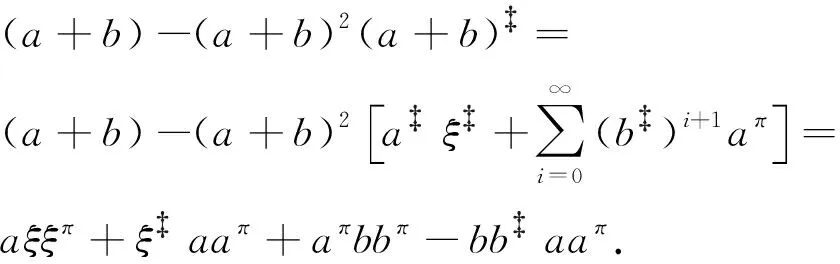
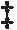
(16)

推论5令a,b∈A×.如果ab=ba,那么a+b∈A×当且仅当1+a×b∈A×.

证明由于ab=ba,我们有a2b=aba和b2a=bab,由定理4即可证得.

3 反三角矩阵

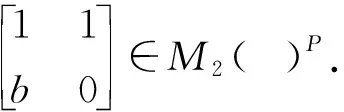
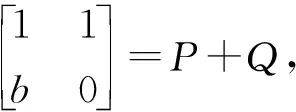
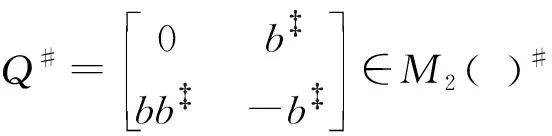
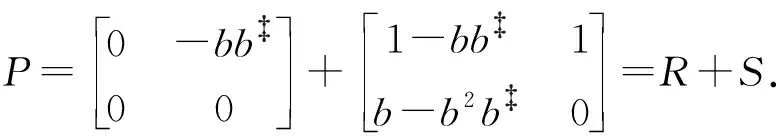
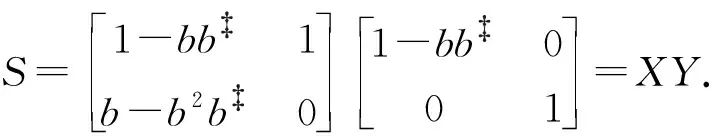
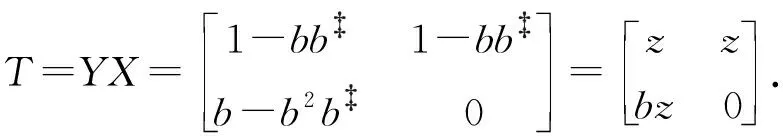
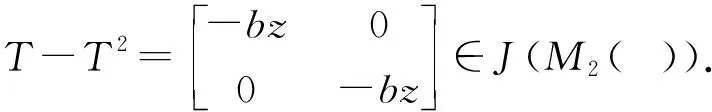
下面可以得到：

定理5令a,b∈A×.如果

(1)1-bb×-aa×b∈A-1；

(2)ab=ba,

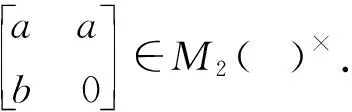
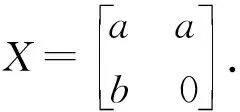
第1步.令

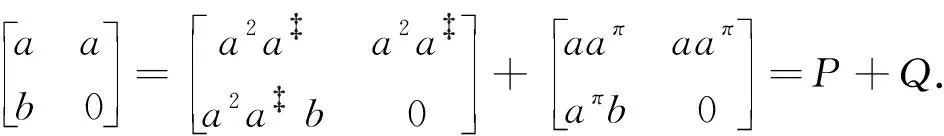
由于Q2∈J(M2(A)),那么Q2-Q3Q=Q2(1-Q2)∈J(M2(A)).根据推论4,我们有Q∈M2(A)P.

由[7，定理5.4]可得,X∈M2(A)P.

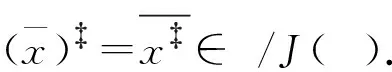
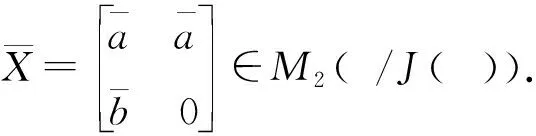
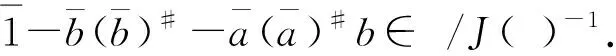
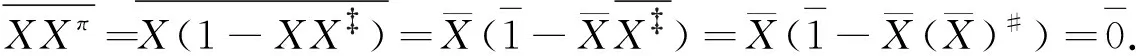
因此XXπ∈J(M2(A)).根据引理2,X∈M2(A)×.